एक बार फिर छंटाई के बारे में

पिछले विषय, एल्गोरिदम की जटिलता का आकलन करने के बारे में, बेहद सकारात्मकता का मूल्यांकन किया गया था। इससे, मैं यह निष्कर्ष निकाल सकता हूं कि बुनियादी एल्गोरिदम का विषय बहुत दिलचस्प है। आज मैं आपको एल्गोरिदम को सॉर्ट करने वाले भाग से परिचित कराना चाहता हूं। यह हैर के लिए बुनियादी एल्गोरिदम के बारे में लिखना गंभीर नहीं है, लेकिन यह अभी भी शैल सॉर्टिंग, एक पिरामिड और त्वरित एक के बारे में बात करने लायक है। (यदि कोई मूल तरीकों के बारे में पढ़ने में रुचि रखता है, तो यहां आपका स्वागत है )

प्रभावी छँटाई के तरीके

घटती दूरी के साथ आवेषण छाँटना (शेल छँटाई)

1959 में, शेल ने सरल आवेषण के साथ छंटाई को गति देने का एक तरीका प्रस्तावित किया। सबसे पहले, k ₁ तत्वों द्वारा अलग किए गए तत्वों के प्रत्येक समूह को अलग-अलग क्रमबद्ध किया जाता है। इस प्रक्रिया को k ₁ छँटाई कहा जाता है। पहले पास के बाद, तत्वों के समूहों पर विचार किया जाता है, लेकिन पहले से ही k ₂ (k ₂ <k ₁ ) स्थान दिए गए हैं, और इन समूहों को अलग से भी सॉर्ट किया जाता है। इस प्रक्रिया को k ₂ छँटाई कहा जाता है। यह कई पुनरावृत्तियों को किया जाता है, और अंत में छंटाई चरण 1 के बराबर हो जाता है।
एक वाजिब सवाल उठता है: क्या कई पास करने की लागत सभी संभावित तत्वों से अधिक होगी, जिनमें से प्रत्येक को हल किया जाएगा? हालांकि, तत्वों के एक समूह के प्रत्येक छंटाई या तो उनमें से एक अपेक्षाकृत कम संख्या से संबंधित है, या तत्व पहले से ही आंशिक रूप से क्रमबद्ध हैं, इसलिए आपको अपेक्षाकृत कुछ क्रमपरिवर्तन करने की आवश्यकता है।
जाहिर है, विधि एक क्रमबद्ध सरणी की ओर ले जाती है, और यह समझना आसान है कि पिछले पुनरावृत्तियों के कारण प्रत्येक चरण पर कम काम करने की आवश्यकता है (क्योंकि प्रत्येक k _मैं छंटनी दो समूहों को जोड़ती है जो पिछले k _i-1 छँटाई द्वारा छांटे जाते हैं)। यह भी स्पष्ट है कि दूरियों का कोई भी क्रम स्वीकार्य है, यदि उनमें से केवल एक ही एकता के बराबर है। यह इतना स्पष्ट नहीं है कि विधि बेहतर काम करती है यदि घटती दूरियों को दो की शक्ति से अलग चुना जाता है।
हम दूरी के एक अनियंत्रित अनुक्रम के लिए एक एल्गोरिथ्म प्रस्तुत करते हैं। कुल में, T की दूरी h ₁ , h ₂ , ..., h _T की स्थिति को संतुष्ट करेगा: h _T = 1, h _{i + 1} <h _i ।

1. प्रक्रिया ShellSort ;
2. स्थिरांक
3. टी = 5 ;
4. वर
5. i , j , k , m : longint ;
6. x : longint ;
7. एच : पूर्णांक की सरणी [ 1 .. 5 ] ;
8. शुरू करना
9. h [ १ ] : = ३१ ; h [ २ ] : = १५ ; h [ ३ ] : = = ; h [ २ ] : = ३ ; h [ १ ] : = १ ;
10. एम के लिए : = 1 से टी करते हैं
11. शुरू करना
12. k : = h [ m ] ;
13. i : = k to N do
14. शुरू करना
15. x : = एक [ i ] ;
16. j : = i - k ;
17. जबकि ( j> = k ) और ( x <a [ j ] ) करते हैं
18. शुरू करना
19. एक [ जे + के ] : = एक [ जे ] ;
20. j : = j - k ;
21. अंत ;
22. if ( j> = k ) या ( x> = a [ j ] ) तो
23. [ a + j + k ] : = x
24. अन्यथा
25. शुरू करना
26. एक [ जे + के ] : = एक [ जे ] ;
27. एक [ जे ] : = एक्स ;
28. अंत ;
29. अंत ;
30. अंत ;
31. अंत ;

इस एल्गोरिथ्म का विश्लेषण एक जटिल गणितीय समस्या है, जिसका अभी भी पूर्ण समाधान नहीं हुआ है। फिलहाल, यह ज्ञात नहीं है कि दूरी का कौन सा क्रम सबसे अच्छा परिणाम देता है, लेकिन यह ज्ञात है कि दूरी एक दूसरे के गुणक नहीं होनी चाहिए। यह आवश्यक है ताकि अगला मार्ग उन दो अनुक्रमों को संयोजित न करे जो पहले नहीं हुए थे। वास्तव में, यह वांछनीय है कि अनुक्रम जितनी बार संभव हो सके। यह निम्नलिखित प्रमेय के साथ जुड़ा हुआ है: यदि k _i सॉर्टिंग के बाद अनुक्रम k _{i + 1} सॉर्टिंग के अधीन है, तो यह k _i सॉर्ट किया गया रहता है।
नॉट निम्नलिखित अनुक्रमों (क्रमिक रूप से कम) में से एक का उपयोग करके क्रमिक रूप से घटती दूरियों का उपयोग करने का सुझाव देता है: 1,4,13,40,121, ..., जहां h _i-1 = 3 * h _i +1 या 1,3,7,15, 31, ..., जहां h _i-1 = 2 * h _i +1 है। बाद के मामले में, एक गणितीय अध्ययन से पता चलता है कि शेल एल्गोरिथ्म द्वारा एन तत्वों को सॉर्ट करते समय, लागत ^1.2 एन के समानुपातिक हैं। यद्यपि यह एन ^{2 की} तुलना में बहुत बेहतर है, हम इस पद्धति में नहीं करेंगे, क्योंकि यहां तक ​​कि तेज एल्गोरिदम भी हैं।

पिरामिड सॉर्ट (टूर्नामेंट सॉर्ट)

चयन द्वारा सरल छंटाई एन तत्वों के बीच सबसे छोटी कुंजी को फिर से चुनने पर आधारित है, फिर शेष एन -1 तत्वों के बीच, आदि। जाहिर है, ऐसे तत्वों के बीच सबसे छोटी कुंजी को खोजने के लिए, जिन्हें आपको एन -1 तुलना की आवश्यकता है, एन -1 तत्वों में से आपको एन -2 तुलना की आवश्यकता है, आदि। जाहिर है, पहले एन -1 प्राकृतिक संख्या का योग है (एन ^2- एन) / 2। यह छँटाई तभी सुधारी जा सकती है जब प्रत्येक देखने के बाद आप केवल एक छोटे से तत्व की तुलना में अधिक जानकारी सहेजते हैं। उदाहरण के लिए, एन / 2 तुलना आपको प्रत्येक जोड़ी में छोटी कुंजी निर्धारित करने की अनुमति देती है, अन्य एन / 4 तुलनाएं पहले से मिली छोटी कुंजी के प्रत्येक जोड़ी में छोटी कुंजी देंगी, आदि। 12,18,42,44,55,67,94,6 की सरणी पर विचार करें। N-1 तुलना करने के बाद, हम एक चयन ट्री बना सकते हैं, जिसकी जड़ में सबसे छोटी कुंजी है।

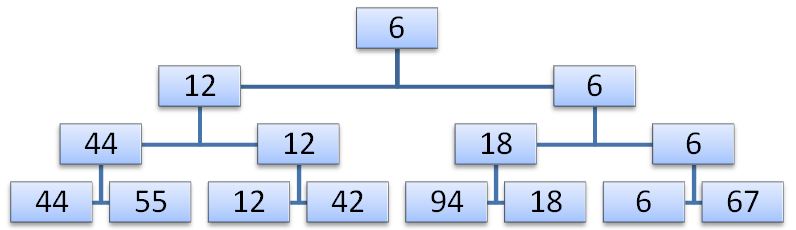
दूसरे चरण में सबसे छोटी कुंजी के अनुरूप पथ के साथ नीचे उतरना होता है और इसे पेड़ की पत्ती में एक खाली स्थिति के साथ या मध्यवर्ती नोड में किसी अन्य शाखा से एक तत्व के साथ प्रतिस्थापित किया जाता है।


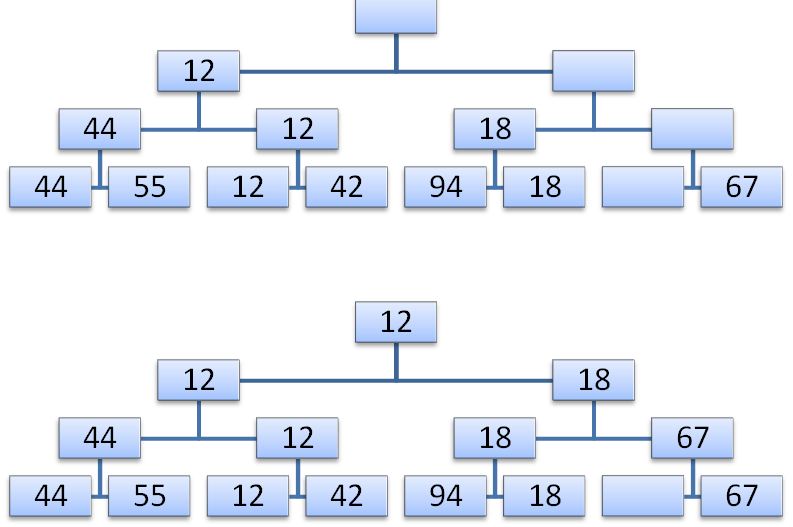
अब पेड़ की जड़ में तत्व अगली सबसे छोटी कुंजी होगी। अब आप इसे हटा सकते हैं। एन ऐसे कदमों के बाद, कुंजी के साथ कोई भी नोड पेड़ में नहीं रहेगा, और छंटनी की प्रक्रिया वहां समाप्त हो जाएगी। जाहिर है, एन चरणों में से प्रत्येक में, लॉग (एन) तुलना की आवश्यकता होती है, इसलिए पूरी प्रक्रिया में एन * लॉग (एन) प्राथमिक संचालन (पेड़ के निर्माण के लिए आवश्यक एन चरणों के अतिरिक्त) के आदेश की आवश्यकता होती है। यह न केवल एन ² चरणों की आवश्यकता वाले सरल तरीकों की तुलना में एक महत्वपूर्ण सुधार है, बल्कि शेल के साथ एन ^1.2 चरणों की भी आवश्यकता है। स्वाभाविक रूप से, इस एल्गोरिथ्म में प्रारंभिक चरणों की जटिलता अधिक है: पिछले चरण से सभी जानकारी को बचाने के लिए, आपको कुछ पेड़ का उपयोग करने की आवश्यकता है। अब हमें इस जानकारी को प्रभावी ढंग से व्यवस्थित करने का एक तरीका खोजने की जरूरत है।
सबसे पहले, आपको खाली मूल्यों को संग्रहीत करने की आवश्यकता से छुटकारा पाना होगा, जो अंत में, पूरे पेड़ को भर देता है और बड़ी संख्या में अनावश्यक तुलना करता है। फिर आपको 2 * N-1 के बजाय पेड़ को मेमोरी में N इकाइयों पर कब्जा करने का तरीका खोजने की जरूरत है, जैसा कि आंकड़ों में होता है। दोनों लक्ष्यों को हीप्सर्ट एल्गोरिथ्म में हासिल किया गया था, इसलिए इसके आविष्कारक विलियम्स द्वारा नामित किया गया था। यह एल्गोरिथ्म नियमित टूर्नामेंट सॉर्टिंग में एक क्रांतिकारी सुधार है।
एक पिरामिड (हीप) कुंजियों का एक क्रम है H _L , h _{L + 1} , ..., h _R (L such0), जैसे कि h _i <h _{2i + 1} और h _i <h _{2i + 2} , i = L ... R / 2-1। यह पता चला है कि किसी भी बाइनरी ट्री को एक सरणी के रूप में दर्शाया जा सकता है, जैसा कि चित्र में दिखाया गया है (इस मामले में, पिरामिड का शीर्ष इसका सबसे छोटा तत्व होगा)।

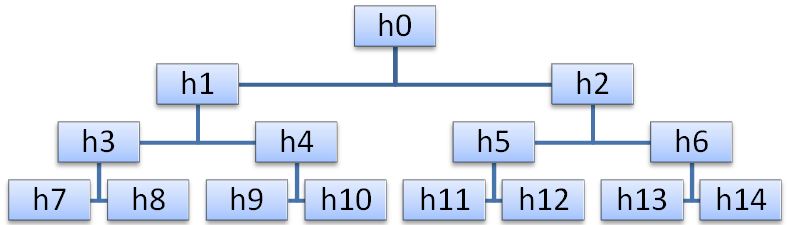
पिरामिड विस्तार एल्गोरिथ्म काफी सरल है। नया पिरामिड निम्नानुसार प्राप्त किया जाता है: सबसे पहले, जोड़े गए तत्व x को पिरामिड के शीर्ष पर रखा जाता है, और फिर इसे नीचे उतारा जाता है, जो कि दो वंशों में से सबसे छोटे के साथ इंटरचेंज करता है, जो तदनुसार बढ़ता है।


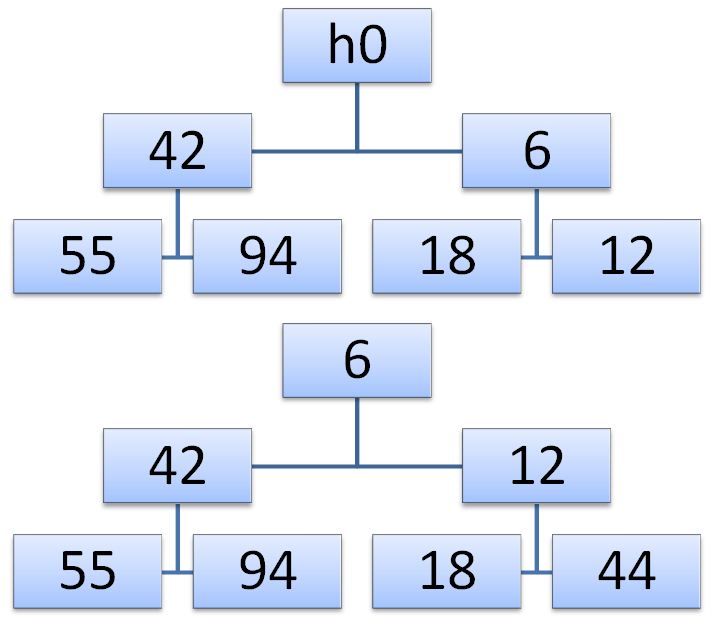
हमारे उदाहरण में, हम पिरामिड का विस्तार संख्या _{0 0} = 44 के साथ करेंगे। पहले, कुंजी 44 6 के साथ स्थान बदलती है, और फिर 12 के साथ। परिणामस्वरूप, हमें वांछित पेड़ मिलता है। हम सूचकांक की एक जोड़ी के संदर्भ में एक sieving एल्गोरिदम तैयार करते हैं i, प्रत्येक sieving कदम पर बदले गए तत्वों के अनुरूप।
जिस विधि पर हम विचार करेंगे वह फ्लोयड द्वारा प्रस्तावित किया गया था। विधि का आधार सिफ्ट प्रक्रिया (सिफ्टिंग) है। अगर हमारे पास एक सरणी h ₁ ... h _{N है} , तो इसके तत्वों के साथ m = N div 2 से N तक के गुण पहले से ही एक पिरामिड बनाते हैं (क्योंकि इन तत्वों में i, j जोड़े नहीं हैं जैसे कि j = 2 * i + 1 या j = 2 * i + 2)। ये तत्व पिरामिड की निचली पंक्ति का निर्माण करेंगे। ध्यान दें कि नीचे की पंक्ति में कोई आदेश देने की आवश्यकता नहीं है। फिर शुरू होता है पिरामिड के विस्तार की प्रक्रिया। इसके अलावा, एक चरण में केवल एक तत्व इसमें शामिल किया जाएगा, और इस तत्व को स्क्रीनिंग प्रक्रिया का उपयोग करके इसकी जगह पर रखा जाएगा, जिसे अब हम विचार करेंगे।

1. प्रक्रिया sift ( एल , आर : पूर्णांक ) ;
2. वर
3. i , j : पूर्णांक ;
4. x : longint ;
5. शुरू करना
6. मैं : = एल ;
7. j : = 2 * i ;
8. x : = एक [ i ] ;
9. if ( j <R ) और ( [[ j ] < [ j + 1 ] ) तो
10. j : = j + 1 ;
11. जबकि ( j < = R ) और ( x <a [ j ] ) करते हैं
12. शुरू करना
13. एक [ i ] : = एक [ जे ] ;
14. i : = j ;
15. j : = 2 * j ;
16. if ( j <R ) और ( [[ j ] < [ j + 1 ] ) तो
17. j : = j + 1 ;
18. अंत ;
19. [ a i ] : = x ;
20. अंत ;

पिरामिड प्राप्त करने की प्रक्रिया को निम्नानुसार वर्णित किया जा सकता है:

1. एल : = ( एन डिव 2 ) + 1 ;
2. आर : = एन ;
3. जबकि एल> 1 करते हैं
4. शुरू करना
5. एल : = एल - 1 ;
6. sift ( एल , आर ) ;
7. अंत ;

हमें मिलने वाला पिरामिड इस तथ्य की विशेषता है कि सबसे बड़ी (और सबसे छोटी नहीं) कुंजी इसके शीर्ष पर संग्रहीत की जाएगी। इसके अलावा, परिणामस्वरूप सरणी पूरी तरह से ऑर्डर नहीं की जाएगी। पूर्ण क्रम को प्राप्त करने के लिए, एक और एन स्क्रीनिंग करना आवश्यक है और उनमें से प्रत्येक के बाद शीर्ष से एक और तत्व निकालने के लिए। सवाल यह है कि ऊपर से हटाए गए तत्वों को कहां संग्रहीत किया जाए। इस समस्या का एक सुंदर सुंदर समाधान है: हमें पिरामिड के अंतिम तत्व (हम इसे x कहेंगे) को लेने की आवश्यकता है, पिरामिड के शीर्ष से तत्व को x के नीचे से मुक्त करने की स्थिति में लिखें, और अगले स् तर से तत्व x को सही स्थिति में रखें। इस प्रक्रिया को निम्नानुसार वर्णित किया जा सकता है:

1. जबकि आर> 1 करते हैं
2. शुरू करना
3. x : = एक [ 1 ] ;
4. एक [ 1 ] : = ए [ आर ] ;
5. ए [ आर ] : = एक्स ;
6. आर : = आर - 1 ;
7. sift ( एल , आर ) ;
8. अंत ;

इस प्रकार, पिरामिड छँटाई एल्गोरिथ्म निम्नलिखित कोड द्वारा प्रतिनिधित्व किया जा सकता है:

1. प्रक्रिया HeapSort ;
2. प्रक्रिया sift ( एल , आर : पूर्णांक ) ;
3. वर
4. i , j : पूर्णांक ;
5. x : longint ;
6. शुरू करना
7. मैं : = एल ;
8. j : = 2 * i ;
9. x : = एक [ i ] ;
10. if ( j <R ) और ( [[ j ] < [ j + 1 ] ) तो
11. j : = j + 1 ;
12. जबकि ( j < = R ) और ( x <a [ j ] ) करते हैं
13. शुरू करना
14. एक [ i ] : = एक [ जे ] ;
15. i : = j ;
16. j : = 2 * j ;
17. if ( j <R ) और ( [[ j ] < [ j + 1 ] ) तो
18. j : = j + 1 ;
19. अंत ;
20. [ a i ] : = x ;
21. अंत ;
22. वर
23. एल , आर : पूर्णांक ;
24. x : longint ;
25. शुरू करना
26. एल : = ( एन डिव 2 ) + 1 ;
27. आर : = एन ;
28. जबकि एल> 1 करते हैं
29. शुरू करना
30. एल : = एल - 1 ;
31. sift ( एल , आर ) ;
32. अंत ;
33. जबकि आर> 1 करते हैं
34. शुरू करना
35. x : = एक [ 1 ] ;
36. एक [ 1 ] : = ए [ आर ] ;
37. ए [ आर ] : = एक्स ;
38. आर : = आर - 1 ;
39. sift ( एल , आर ) ;
40. अंत ;
41. अंत ;

इस एल्गोरिथ्म में, बड़े तत्वों को पहले बाईं ओर sifted किया जाता है, और उसके बाद ही छांटे गए सरणी के दाईं ओर अंतिम स्थिति पर कब्जा होता है। इस वजह से, ऐसा लग सकता है कि पिरामिड की छँटाई की दक्षता बहुत अधिक नहीं है। वास्तव में, तत्वों की एक छोटी संख्या को सॉर्ट करने के लिए अन्य एल्गोरिदम का उपयोग करना बेहतर है, लेकिन बड़े एन के लिए यह छंटाई बहुत प्रभावी है।
सबसे खराब स्थिति में, पिरामिड बनाने के चरण में एन / 2 शिफ्टिंग चरणों की आवश्यकता होती है, और प्रत्येक चरण में तत्वों को लॉग (एन / 2), लॉग (एन / 2 + 1), ..., लॉग (एन -1) पदों के माध्यम से सिफ्ट किया जाता है। फिर सॉर्टिंग चरण के लिए n-1 स्क्रीनिंग की आवश्यकता होती है जिसमें लॉग (N-1), लॉग (N-2), ..., 1 स्थानान्तरण से अधिक नहीं है। इसके अलावा, पिरामिड के ऊपर से तत्वों को उसके स्थान पर रखने के लिए n-1 स्थानान्तरण की आवश्यकता होगी। यह पता चला है कि सबसे खराब स्थिति में भी, पिरामिडल सॉर्टिंग के लिए एन * लॉग (एन) स्थानांतरण की आवश्यकता होती है। यह संपत्ति इस एल्गोरिथ्म की सबसे महत्वपूर्ण विशिष्ट विशेषता है।
सर्वोत्तम प्रदर्शन की उम्मीद की जा सकती है अगर तत्व शुरू में रिवर्स ऑर्डर में हों। फिर पिरामिड बनाने के चरण में शिपमेंट की आवश्यकता नहीं होगी। स्थानान्तरण की औसत संख्या एन / 2 * लॉग (एन) है, और इस मूल्य से विचलन काफी छोटे हैं।

त्वरित छाँट

पिछले दो तरीके सम्मिलन और चयन के सिद्धांतों पर आधारित थे। यह एक तीसरे पर विचार करने का समय है, जो विनिमय के सिद्धांत पर आधारित है। बबल सॉर्टिंग सभी तीन सरल एल्गोरिदम के बीच सबसे खराब रही, हालांकि, एक्सचेंज सॉर्टिंग में सुधार एरेज़ को छांटने के लिए सबसे अच्छा ज्ञात तरीका प्रदान करता है।
त्वरित छंटाई का निर्माण इस तथ्य पर आधारित है कि अधिकतम दक्षता प्राप्त करने के लिए, सबसे दूरस्थ पदों के बीच आदान-प्रदान करना वांछनीय है। मान लीजिए कि हमारे पास एन तत्व उल्टे क्रम में व्यवस्थित हैं। आप उन्हें केवल एन / 2 एक्सचेंजों में सॉर्ट कर सकते हैं, सबसे पहले सबसे बाएं और दाएं तत्वों का आदान-प्रदान कर सकते हैं, और फिर धीरे-धीरे दोनों तरफ सरणी के अंदर जा सकते हैं। बेशक, यह विधि केवल तभी काम करेगी जब सरणी के तत्वों को रिवर्स ऑर्डर में आदेश दिया जाएगा। फिर भी, यह इस विचार पर ठीक है कि विचाराधीन पद्धति का निर्माण किया गया है।
आइए ऐसे एल्गोरिदम को लागू करने का प्रयास करें: किसी भी तत्व को बेतरतीब ढंग से चुनें (चलो इसे एक्स कहते हैं)। जब तक हम तत्व को _i > x नहीं पाते हैं, तब तक हम बाईं ओर स्थित सरणी को देखेंगे और तब तक दाईं ओर, जब तक हमें तत्व नहीं मिल जाता। _j <x फिर हम दो पाए गए तत्वों का आदान-प्रदान करेंगे और इस प्रक्रिया को तब तक जारी रखेंगे जब तक कि दोनों व्यूज़ सरणी के बीच में कहीं नहीं मिलते। नतीजतन, हम एक सरणी को दो भागों में विभाजित करते हैं: बाईं ओर, कुंजी के साथ छोटी (या बराबर) x, और दाईं ओर की कुंजियों के साथ बड़ा (या बराबर) x। हम प्रक्रिया के रूप में पृथक्करण प्रक्रिया तैयार करते हैं:

1. प्रक्रिया विभाजन ;
2. वर
3. i , j : पूर्णांक ;
4. डब्ल्यू , एक्स : पूर्णांक ;
5. शुरू करना
6. i : = 1 ;
7. j : = n ;
8. // बेतरतीब ढंग से x का चयन करें
9. दोहराएं
10. जबकि एक [ i ] <x करते हैं
11. i : = i + 1 ;
12. जबकि x < [ j ] करते हैं
13. j : = j - 1 ;
14. अगर मैं < = j तब
15. शुरू करना
16. w : = एक [ i ] ;
17. एक [ i ] : = एक [ जे ] ;
18. एक [ जे ] : = डब्ल्यू ;
19. i : = i + 1 ;
20. j : = j - 1 ;
21. अंत ;
22. UNTIL i> j ;
23. अंत ;

अब याद रखें कि हमारा लक्ष्य केवल सरणी को विभाजित करना नहीं है, बल्कि इसे क्रमबद्ध करना भी है। वास्तव में, पृथक्करण से छँटाई तक, केवल एक छोटा सा चरण है: सरणी को विभाजित करने के बाद, आपको दोनों भागों में एक ही प्रक्रिया को लागू करना होगा, फिर भागों के कुछ हिस्सों, आदि तक, प्रत्येक भाग में एक तत्व होता है।

1. प्रक्रिया प्रकार ( एल , आर : पूर्णांक ) ;
2. वर
3. i , j : पूर्णांक ;
4. डब्ल्यू , एक्स : लॉन्गिंट ;
5. शुरू करना
6. मैं : = एल ;
7. j : = R ;
8. x : = a [ ( L + R ) div 2 ] ;
9. दोहराएं
10. जबकि एक [ i ] <x करते हैं
11. i : = i + 1 ;
12. जबकि x < [ j ] करते हैं
13. j : = j - 1 ;
14. अगर मैं < = j तब
15. शुरू करना
16. w : = एक [ i ] ;
17. एक [ i ] : = एक [ जे ] ;
18. एक [ जे ] : = डब्ल्यू ;
19. i : = i + 1 ;
20. j : = j - 1 ;
21. अंत ;
22. UNTIL i> j ;
23. यदि L <j तब
24. सॉर्ट ( एल , जे ) ;
25. अगर मैं <आर तो
26. सॉर्ट ( i , R ) ;
27. अंत ;
28. प्रक्रिया QuickSort ;
29. शुरू करना
30. सॉर्ट ( 1 , एन ) ;
31. अंत ;

क्विकॉर्ट की प्रभावशीलता का अध्ययन करने के लिए, आपको सबसे पहले जुदाई प्रक्रिया के व्यवहार की जांच करनी चाहिए। X के अलग मूल्य को चुनने के बाद, संपूर्ण सरणी स्कैन की जाती है, इसलिए वास्तव में एन तुलना की जाएगी। यदि हम भाग्यशाली हैं, और मध्य (सरणी का मध्य तत्व) को हमेशा सीमा के रूप में चुना जाता है, तो प्रत्येक पुनरावृत्ति सरणी को आधे में विभाजित करता है, और आवश्यक पास की संख्या लॉग (एन) के बराबर होती है। फिर तुलनाओं की कुल संख्या एन * लॉग (एन) है, और एक्सचेंजों की कुल संख्या एन * लॉग (एन) / 6 है।
बेशक, कोई यह उम्मीद नहीं कर सकता है कि एक मंझले की पसंद के साथ यह हमेशा इतना भाग्यशाली होगा। सख्ती से, इस की संभावना 1 / N है। लेकिन यह दिखाया गया है कि त्वरित छँटाई की अपेक्षित दक्षता केवल 2 * ln (2) के कारक से इष्टतम से भी बदतर है।
यहां तक ​​कि क्विकसॉर्ट एल्गोरिथ्म के भी नुकसान हैं। छोटे एन में, इसके प्रदर्शन को संतोषजनक माना जा सकता है, लेकिन इसका लाभ प्रसंस्करण खंडों के लिए एक सरल विधि को जोड़ने में आसानी से निहित है। सबसे खराब स्थिति समस्या बनी हुई है। मान लीजिए कि हर बार साझा सेगमेंट में सबसे बड़ा मूल्य अलग करने वाले तत्व के रूप में चुना गया है। फिर प्रत्येक चरण क्रमशः N तत्वों के एक टुकड़े को 1 और N-1 तत्वों के दो अनुक्रमों में विभाजित करेगा। जाहिर है, सबसे खराब स्थिति में, व्यवहार का अनुमान एन ² के मूल्य से लगाया जाता है। सबसे खराब स्थिति से बचने के लिए, तत्व x को साझा खंड के तीन मूल्यों के मध्य के रूप में चुनने का सुझाव दिया गया था। इस तरह का जोड़ सामान्य मामले में एल्गोरिथ्म को नीचा नहीं करता है, लेकिन इसके सबसे खराब मामले को बेहतर बनाता है।