हेयुरिस्टिक निवेश पोर्टफोलियो का गठन एल्गोरिदम

मान लीजिए कि कई संभावित निवेशों में निवेश करने के लिए हमारे पास $ 100 मिलियन हैं। इनमें से प्रत्येक निवेश का एक अलग मूल्य और एक अलग अपेक्षित रिटर्न है। हमें तय करना चाहिए कि अधिकतम लाभ प्राप्त करने के लिए पैसे कैसे खर्च करें।
इस प्रकार के कार्यों को पोर्टफोलियो निर्माण कार्य कहा जाता है। हमारे पास कई पद (निवेश) हैं जो एक निश्चित आकार के पोर्टफोलियो ($ 100 मिलियन) में फिट होने चाहिए। प्रत्येक स्थिति की अपनी लाभप्रदता है। आपको ऐसे पदों का एक समूह ढूंढना होगा जो पोर्टफोलियो में रखे गए हों और अधिकतम लाभ दें।
आप में से बहुत से लोग कहेंगे कि यहाँ किसी भी प्रकार की कोई आवश्यकता नहीं है, और यह बहुत संभव है कि यह संपूर्ण खोज के साथ संभव है। दूसरे लोग कहेंगे कि पूर्ण खोज की आवश्यकता नहीं है, क्योंकि शाखाओं और सीमाओं की एक विधि है। लेकिन क्या होगा यदि संभावित निवेश की संख्या 65 है? पूर्ण निर्णय वृक्ष में 7 * 10 ^ 19 से अधिक नोड्स होते हैं। मान लीजिए कि शाखा और बाउंड विधि इन नोड्स के एक प्रतिशत के दसवें हिस्से पर प्रसारित होती है, और कंप्यूटर प्रति सेकंड एक लाख नोड्स की जांच करता है। इन शर्तों के तहत, समस्या को हल करने में 2 मिलियन से अधिक वर्षों का समय लगेगा। यह ऐसे जटिल कार्यों के लिए है जिनका उपयोग सांख्यिकी में किया जाता है। यदि आप रुचि रखते हैं, तो आपका स्वागत है बिल्ली के लिए।

पहाड़ी पर चढ़ना

पहाड़ी पर चढ़ने की विधिवत विधि वर्तमान समाधान में परिवर्तन करती है, इसे लक्ष्य के जितना करीब हो सके उतना आगे बढ़ाना। इस प्रक्रिया को पहाड़ी चढ़ाई कहा जाता है, क्योंकि यह एक खोए हुए यात्री की तरह दिखता है जो रात में पहाड़ की चोटी तक पहुंचने की कोशिश करता है। भले ही दूर में कुछ देखने के लिए पहले से ही अंधेरा हो, वह लगातार ऊपर की ओर बढ़ते हुए, पहाड़ की चोटी तक पहुंचने की कोशिश कर सकता है।
बेशक, एक मौका है कि यात्री एक छोटी पहाड़ी की चोटी पर रुक जाएगा और एक चोटी तक नहीं पहुंचेगा। इस हेयुरिस्टिक विधि का उपयोग करते समय यह समस्या मौजूद है। एल्गोरिथ्म एक समाधान मिल सकता है जो स्थानीय रूप से इष्टतम है, लेकिन सबसे अच्छा संभव समाधान नहीं है।
निवेश पोर्टफोलियो बनाने के कार्य में, लक्ष्य निर्धारित सीमा से अधिक नहीं के कुल मूल्य के साथ पदों का एक सेट चुनना है, और कुल लाभ जितना संभव हो उतना बड़ा होना चाहिए। इस कार्य के लिए पहाड़ी पर चढ़ने के आंकड़े एक ऐसे पद का चयन करते हैं जो हर कदम पर अधिकतम लाभ देता है। इसी समय, निर्णय बेहतर लाभ को अधिकतम करने के लक्ष्य को पूरा करेगा।
एल्गोरिथ्म पहले समाधान के लिए अधिकतम लाभ के साथ स्थिति जोड़ता है, फिर अधिकतम लाभ के साथ अगली स्थिति को जोड़ा जाता है (बशर्ते कि पूर्ण मूल्य स्वीकार्य सीमा के भीतर रहता है)। अधिकतम लाभ के साथ पदों को जोड़ना तब तक जारी रहेगा जब तक कि मूल्य की सीमा समाप्त नहीं हो जाती।
नीचे निवेश की सूची के लिए, कार्यक्रम पहले ए का चयन करेगा, क्योंकि इसमें सबसे बड़ा रिटर्न ($ 9 मिलियन) है। तब लेनदेन सी का चयन किया जाता है क्योंकि इसमें सबसे बड़ा लाभ शेष ($ 8 मिलियन) होता है। इस समय, स्वीकार्य 100 मिलियन में से, 93 मिलियन पहले ही खर्च किए जा चुके हैं, और एल्गोरिथ्म अब अपने लेनदेन का चयन करने में सक्षम नहीं होगा। इस हेयुरिस्टिक का उपयोग करके गणना किए गए समाधान में ए और सी तत्व शामिल हैं, इसकी लागत 93 मिलियन है और यह 17 मिलियन का लाभ कमाता है।

चढ़ाई के आंकड़े बहुत तेज़ी से एक पोर्टफोलियो भरते हैं। यदि तत्वों को शुरू में घटते लाभ के क्रम में आदेश दिया जाता है, तो एल्गोरिथ्म की जटिलता ओ (एन) के बारे में है। कार्यक्रम केवल सूची में घूमता है, अधिकतम लाभ के साथ पदों को जोड़ता है, जब तक कि धन की सीमा समाप्त नहीं होती है। यदि सूची को क्रमबद्ध नहीं किया गया है, तो इस एल्गोरिथ्म की जटिलता एन * लॉग (एन) है। यह एक पेड़ के सभी नोड्स को पूरी तरह से घेरने के लिए आवश्यक ओ (2 ^ एन) चरणों की तुलना में बहुत बेहतर है। 20 पदों के लिए, यह अनुमानी लगभग 400 चरणों का उपयोग करता है, शाखाओं और सीमाओं की विधि - कई हजार, और संपूर्ण खोज - 2 मिलियन से अधिक।

कम से कम लागत विधि

रणनीति, जो कुछ मायनों में पहाड़ी चढ़ाई विधि के विपरीत है, को कम से कम लागत विधि कहा जाता है। प्रत्येक चरण में यथासंभव समाधान को लक्ष्य के करीब लाने के बजाय, आप समाधान की लागत को कम करने का प्रयास कर सकते हैं। प्रत्येक चरण में एक निवेश पोर्टफोलियो के गठन के साथ उदाहरण में, न्यूनतम लागत वाली स्थिति को समाधान में जोड़ा जाता है।
यह रणनीति समाधान में अधिक से अधिक स्थान देगी। यह अच्छी तरह से काम करता है अगर सभी पदों में लगभग समान मूल्य है। लेकिन अगर एक महंगा लेनदेन बड़ा मुनाफा लाता है, तो यह रणनीति सबसे अच्छा संभव परिणाम नहीं दे सकती है।
ऊपर उल्लिखित निवेशों के लिए, न्यूनतम लागत रणनीति पहले समाधान के लिए 23 मिलियन मूल्य के लेनदेन ई को जोड़कर शुरू होती है। फिर वह 27 मिलियन डी और 30 मिलियन मूल्य की स्थिति का चयन करती है। इस बिंदु पर, एल्गोरिथम पहले ही 100 में से 80 मिलियन खर्च कर चुका है। मिलियन डॉलर और अब एक भी निवेश नहीं कर सकते।
परिणामी समाधान की लागत 80 मिलियन है और यह 18 मिलियन का लाभ कमाता है। यह उस समाधान की तुलना में एक मिलियन बेहतर है जो पहाड़ी चढ़ाई हमें देता है, लेकिन न्यूनतम लागत एल्गोरिदम हमेशा पहाड़ी चढ़ाई एल्गोरिदम की तुलना में अधिक कुशलता से काम नहीं करता है। कौन सा तरीका सबसे अच्छा समाधान देगा यह विशिष्ट डेटा पर निर्भर करता है।
न्यूनतम लागत और पहाड़ी पर चढ़ने के उत्तराधिकार को लागू करने वाले कार्यक्रमों की संरचना लगभग समान है। एकमात्र अंतर अगली स्थिति का विकल्प है, जिसे मौजूदा समाधान में जोड़ा गया है। अधिकतम लाभ के साथ स्थिति के बजाय न्यूनतम लागत विधि उस स्थिति का चयन करती है जिसमें सबसे कम लागत होती है। चूंकि दोनों विधियां बहुत समान हैं, इसलिए उनकी जटिलता समान है। यदि पदों को ठीक से सॉर्ट किया जाता है, तो दोनों एल्गोरिदम में ओ (एन) के क्रम की जटिलता है। पदों की एक यादृच्छिक व्यवस्था के साथ, उनकी जटिलता ओ (एन * लॉग (एन)) के आदेश की होगी।

संतुलित लाभ

पहाड़ी चढ़ाई की रणनीति में अतिरिक्त पदों के मूल्य को ध्यान में नहीं रखा गया है। वह अधिकतम लाभ के साथ पदों का चयन करती है, भले ही वे महान मूल्य के हों। न्यूनतम लागत रणनीति स्थिति द्वारा लाए गए लाभ को ध्यान में नहीं रखती है। वह कम लागत पर वस्तुओं का चयन करती है, भले ही उन्हें थोड़ा लाभ हो।
बैलेंस्ड प्रॉफिट हेयुरेटिक्स यह निर्धारित करने के लिए कि किन पदों को चुनने की आवश्यकता है, दोनों लाभ और स्थिति मूल्य की तुलना करते हैं। प्रत्येक चरण में, हेयुरिस्टिक लाभ के उच्चतम अनुपात के साथ तत्व का चयन करता है (बशर्ते कि पोर्टफोलियो में निवेश शामिल होने के बाद, कुल कीमत स्वीकार्य सीमा के भीतर रहेगी)।
हम तालिका में एक नया कॉलम शामिल करते हैं - लाभ / मूल्य का अनुपात। इस दृष्टिकोण के साथ, स्थिति C को पहले चुना गया है क्योंकि इसमें 0.27 का उच्चतम अनुपात है। फिर D को 0.26 के अनुपात और B को 0.20 के अनुपात के साथ जोड़ा जाता है। इस बिंदु पर, 100 मिलियन में से 92 मिलियन खर्च किए गए थे, और समाधान में एक भी स्थिति नहीं जोड़ी जा सकती है।

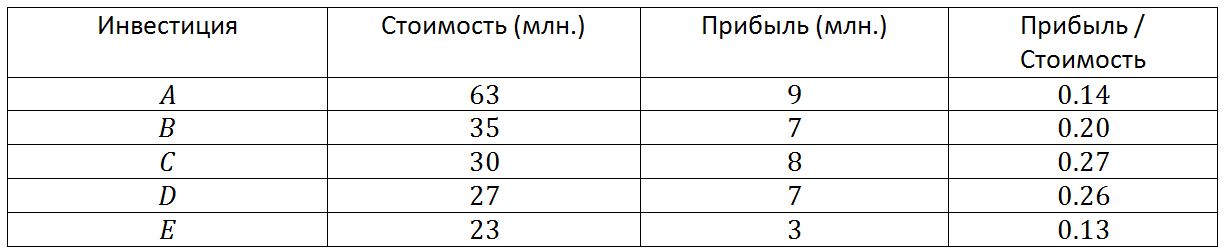
इस समाधान का मूल्य 92 मिलियन है और यह 22 मिलियन का लाभ देता है। यह न्यूनतम लागत पद्धति का उपयोग करते हुए पाए गए समाधान की तुलना में 4 मिलियन बेहतर है और हेयुरिस्टिक पहाड़ी चढ़ाई से प्राप्त समाधान से 5 मिलियन बेहतर है। इसके अलावा, पाया गया समाधान आम तौर पर सभी संभवों में सबसे अच्छा होगा, जो संपूर्ण खोज द्वारा या शाखाओं और सीमाओं की विधि द्वारा खोज की पुष्टि करेगा। लेकिन यह समझना महत्वपूर्ण है कि संतुलित लाभ अभी भी एक अनुमान है, इसलिए, इसकी मदद से, सबसे अच्छा संभव समाधान हमेशा नहीं मिलता है। बहुत बार, यह विधि पहाड़ी पर चढ़ने के तरीकों और न्यूनतम लागत पर पाए जाने वाले समाधानों की तुलना में बेहतर समाधान ढूंढती है, लेकिन ऐसा हमेशा नहीं होता है। कार्यक्रम की संरचना जो संतुलित लाभ के उत्तराधिकार को लागू करती है, पहाड़ी चढ़ाई कार्यक्रमों और न्यूनतम लागत की संरचना के समान है। एकमात्र अंतर वह तरीका है जिससे आप अगली स्थिति का चयन करते हैं जो समाधान में जोड़ा जाता है। इस हेयुरिस्टिक की जटिलता ओ (एन) के लिए आनुपातिक है, जो प्रारंभिक छँटाई के अधीन है। यदि स्थितियां मनमाने ढंग से स्थित हैं, तो एल्गोरिथ्म की जटिलता ओ (एन * लॉग (एन)) होगी।

यादृच्छिक तरीके

यादृच्छिक खोज

एक यादृच्छिक खोज अपने नाम के अनुसार की जाती है। प्रत्येक चरण में, एल्गोरिथ्म एक यादृच्छिक रूप से चयनित स्थिति जोड़ता है जो लागत की सीमाओं को संतुष्ट करता है। इस प्रकार की गणना को मोंटे कार्लो विधि कहा जाता है।
चूंकि एक यादृच्छिक रूप से चयनित समाधान सबसे अच्छा होने की संभावना नहीं है, स्वीकार्य परिणाम प्राप्त करने के लिए, आपको कई बार खोज को दोहराना होगा। हालांकि पहली नज़र में ऐसा लगता है कि एक अच्छा समाधान खोजने की संभावना बहुत कम है, इस पद्धति का उपयोग कभी-कभी आश्चर्यजनक रूप से अच्छे परिणाम उत्पन्न करता है। प्रारंभिक आंकड़ों और जाँच किए गए यादृच्छिक समाधानों की संख्या के आधार पर, यह अनुमानी अक्सर पहाड़ी चढ़ाई के तरीकों और न्यूनतम लागत से बेहतर काम करता है।
यादृच्छिक खोज का लाभ यह है कि इस पद्धति को समझना और लागू करना आसान है। कभी-कभी यह कल्पना करना मुश्किल होता है कि किसी विशिष्ट कार्य के लिए पहाड़ी पर चढ़ने की विधि, न्यूनतम लागत या कम लाभ को कैसे लागू किया जाए, लेकिन यादृच्छिक पर समाधान उत्पन्न करना हमेशा आसान होता है। यहां तक ​​कि अत्यंत जटिल समस्याओं को हल करने के लिए, यादृच्छिक खोज सबसे सरल विधि है।

अनुक्रमिक दृष्टिकोण

एक और रणनीति एक यादृच्छिक समाधान के साथ शुरू करना है और फिर एक सुसंगत सन्निकटन बनाना है। एक बेतरतीब ढंग से उत्पन्न समाधान के साथ शुरू, कार्यक्रम एक यादृच्छिक विकल्प बनाता है। यदि नया समाधान पिछले एक पर एक सुधार है, तो कार्यक्रम परिवर्तन को समेकित करता है और अन्य वस्तुओं की जांच करना जारी रखता है। यदि परिवर्तन समाधान में सुधार नहीं करता है, तो कार्यक्रम इसे मना कर देता है और एक नया प्रयास करता है।
निवेश के पोर्टफोलियो बनाने के कार्य के लिए सुसंगत सन्निकटन की विधि को लागू करना विशेष रूप से सरल है। कार्यक्रम केवल परीक्षण समाधान से एक यादृच्छिक स्थिति का चयन करता है और इसे वर्तमान से हटा देता है। फिर वह बेतरतीब ढंग से निर्णय के लिए पदों को जोड़ता है जब तक कि धन की सीमा समाप्त नहीं होती है। यदि हटाई गई स्थिति में बहुत अधिक लागत थी, तो प्रोग्राम कई स्थानों को जोड़ सकता है, अपनी जगह नहीं।
यादृच्छिक खोज की तरह, इस अनुमान को समझना और लागू करना आसान है। एक जटिल समस्या को हल करने के लिए, पहाड़ी पर चढ़ने, न्यूनतम लागत और कम लाभ के लिए एल्गोरिदम बनाना आसान नहीं है, लेकिन क्रमिक सन्निकटन के लिए एक अनुमानी एल्गोरिथ्म लिखना काफी सरल है।

रुकना पल

यादृच्छिक परिवर्तनों को रोकने के लिए निर्धारित करने के लिए कई अच्छे तरीके हैं। उदाहरण के लिए, निश्चित संख्या में परिवर्तन की अनुमति है। एन तत्वों के एक कार्य के लिए, आप एन या एन ^ 2 यादृच्छिक परिवर्तन कर सकते हैं और फिर कार्यक्रम को रोक सकते हैं।
एक और रणनीति यह है कि जब तक क्रमिक परिवर्तन सुधार न लाएँ तब तक बदलाव करें। जैसे ही कई लगातार परिवर्तन सुधार नहीं देते हैं, कार्यक्रम को रोका जा सकता है।

स्थानीय इष्टतम

यदि कार्यक्रम परीक्षण समाधान में एक यादृच्छिक रूप से चयनित स्थिति की जगह लेता है, तो यह एक ऐसा समाधान ढूंढ सकता है जिसे अब सुधार नहीं किया जा सकता है, लेकिन यह अभी भी सबसे अच्छा संभव समाधान नहीं होगा। एक उदाहरण के रूप में, संभावित निवेश के निम्नलिखित सेट पर विचार करें।

मान लीजिए कि एल्गोरिथ्म बेतरतीब ढंग से प्रारंभिक समाधान के रूप में ए और बी का चयन करता है। इसका मूल्य 90 मिलियन के बराबर होगा, यह 17 मिलियन का लाभ लाएगा।
यदि प्रोग्राम ए या बी को हटा देता है, तो समाधान में उच्च लागत होगी, इसलिए कार्यक्रम केवल एक नई स्थिति जोड़ सकता है। चूंकि A और B के पदों में सबसे बड़ा लाभ है, इसलिए उन्हें किसी अन्य पद के साथ बदलने से कुल लाभ कम हो जाएगा। इस समाधान से गलती से एक स्थिति को हटाने से सुधार कभी नहीं होगा।
सर्वश्रेष्ठ समाधान में C, D, E. की कुल लागत 98 मिलियन है, कुल लाभ 18 मिलियन है। इस समाधान को खोजने के लिए, एल्गोरिदम को एक बार में समाधान से A और B दोनों स्थितियों को निकालना होगा और उनके स्थान पर नए लोगों को जोड़ना होगा।
ऐसे निर्णय, जब छोटे परिवर्तन समाधानों में सुधार नहीं कर सकते हैं, स्थानीय इष्टतम कहलाते हैं। दो तरीके हैं जिनमें कार्यक्रम स्थानीय इष्टतम पर नहीं रुकेगा, लेकिन एक वैश्विक इष्टतम के लिए दिखेगा।
सबसे पहले, कार्यक्रम को बदला जा सकता है ताकि यह समाधान से कई वस्तुओं को हटा दे। यदि प्रोग्राम दो बेतरतीब ढंग से चयनित आइटम हटाता है, तो वह इस उदाहरण के लिए सही समाधान पा सकता है। हालाँकि, बड़े कार्यों के लिए, दो पदों को हटाना आमतौर पर पर्याप्त नहीं होता है। कार्यक्रम को तीन, चार, या शायद अधिक पदों को हटाने की आवश्यकता होगी।
एक सरल तरीका विभिन्न प्रारंभिक समाधानों के साथ अधिक परीक्षण करना है। कुछ शुरुआती समाधान स्थानीय ऑप्टिमा को जन्म दे सकते हैं, लेकिन उनमें से एक वैश्विक इष्टतम प्राप्त करेगा।

एनीलिंग विधि

Annealing विधि ऊष्मागतिकी से उधार ली गई है। एनीलिंग के दौरान, धातु को उच्च तापमान पर गरम किया जाता है। गर्म धातु में अणु तेजी से कंपन करते हैं। यदि धातु को धीरे-धीरे ठंडा किया जाता है, तो अणु ऊपर बनने लगते हैं, जिससे क्रिस्टल बन जाते हैं। इस मामले में, अणु धीरे-धीरे न्यूनतम ऊर्जा के साथ एक राज्य में बदल जाते हैं।
जब धातु ठंडा होता है, तो पड़ोसी क्रिस्टल एक दूसरे के साथ विलय हो जाते हैं। एक क्रिस्टल के अणु अस्थायी रूप से अपनी स्थिति को न्यूनतम ऊर्जा के साथ छोड़ देते हैं और दूसरे क्रिस्टल के अणुओं के साथ संयोजन करते हैं। परिणामस्वरूप बड़े क्रिस्टल की ऊर्जा दो मूल क्रिस्टल की ऊर्जाओं के योग से कम होगी। यदि धातु को धीरे-धीरे पर्याप्त रूप से ठंडा किया जाता है, तो क्रिस्टल बस विशाल हो जाएंगे। अणुओं की अंतिम व्यवस्था में बहुत कम कुल ऊर्जा होगी, इसलिए धातु बहुत मजबूत होगी।
उच्च ऊर्जा अवस्था से शुरू होकर, अणु अंततः एक निम्न ऊर्जा अवस्था तक पहुँच जाते हैं। अपनी अंतिम स्थिति के रास्ते में, वे कई स्थानीय ऊर्जा मिनिमा से गुजरते हैं। प्रत्येक क्रिस्टल संयोजन एक स्थानीय न्यूनतम का प्रतिनिधित्व करता है। क्रिस्टल को केवल छोटे क्रिस्टल की संरचना के अस्थायी समाधान द्वारा न्यूनतम ऊर्जा अवस्था में लाया जा सकता है, जिससे सिस्टम की ऊर्जा बढ़ जाती है, जिसके परिणामस्वरूप क्रिस्टल गठबंधन कर सकते हैं।
एनीलिंग विधि किसी समस्या का सबसे अच्छा समाधान खोजने के लिए एक समान विधि का उपयोग करती है। जब कोई प्रोग्राम किसी समाधान की खोज करता है, तो वह स्थानीय इष्टतम में फंस सकता है। इससे बचने के लिए, वह कभी-कभी समाधान के लिए यादृच्छिक परिवर्तन करती है, भले ही अगला विकल्प तुरंत परिणाम में सुधार न करे। यह प्रोग्राम को स्थानीय इष्टतम से बाहर निकलने और सबसे अच्छा समाधान खोजने की अनुमति देता है।
इन संशोधनों पर ध्यान केंद्रित करने से कार्यक्रम को रोकने के लिए, थोड़ी देर के बाद एल्गोरिथ्म यादृच्छिक परिवर्तन करने की संभावना को बदलता है। एक परिवर्तन करने की संभावना P = 1 / e ^ (E / (k * T)) है, जहां E को सिस्टम में जोड़ा गया "एनर्जी" की मात्रा है, k एक निरंतर समस्या के आधार पर चयनित है, और T "तापमान" के अनुरूप एक परिवर्तनशील है। "।
सबसे पहले, टी का मूल्य काफी अधिक होना चाहिए, इसलिए परिवर्तनों की संभावना भी काफी अधिक होगी। कुछ समय बाद, टी का मूल्य कम हो जाता है, और यादृच्छिक परिवर्तनों की संभावना भी कम हो जाती है। एक बार प्रक्रिया एक ऐसे बिंदु पर पहुंच गई है, जिस पर कोई भी परिवर्तन समाधान में सुधार नहीं कर सकता है और टी का मूल्य इतना छोटा हो जाता है कि यादृच्छिक परिवर्तन बहुत दुर्लभ हैं, एल्गोरिथ्म काम खत्म कर देगा।
निवेशों के पोर्टफोलियो बनाने के कार्य के लिए, E वह मूल्य है जिसके द्वारा परिवर्तन के परिणामस्वरूप लाभ कम हो जाता है। उदाहरण के लिए, यदि हम $ 10 मिलियन के लाभ के साथ एक स्थिति को हटाते हैं और $ 7 मिलियन के लाभ के साथ एक स्थिति के साथ प्रतिस्थापित करते हैं, तो सिस्टम में जोड़ी गई ऊर्जा 3 के बराबर होगी। यदि ई बड़ा है, तो परिवर्तनों की संभावना छोटा है, इसलिए बड़े परिवर्तनों की संभावना नीचे दिए गए।

विधर्मी तरीकों की तुलना

अलग-अलग कार्यों में अलग-अलग विधर्मी तरीके अलग-अलग व्यवहार करते हैं। निवेश के पोर्टफोलियो बनाने की समस्या को हल करने के लिए, संतुलित लाभ का अनुमान काफी अच्छा है, इसकी सादगी को देखते हुए। अनुक्रमिक दृष्टिकोण की रणनीति भी काफी अच्छी तरह से काम करती है, लेकिन इसके लिए बहुत अधिक समय की आवश्यकता होती है। अन्य कार्यों के लिए, कुछ अन्य अनुमान सबसे अच्छे हो सकते हैं, जिनमें से इस अध्याय में विचार नहीं किया गया है।
पाशविक बल और शाखा और बंधे हुए तरीकों की तुलना में हेयुरिस्टिक्स बहुत तेजी से काम करते हैं। कुछ विधर्मी दृष्टिकोण (एक पहाड़ी पर चढ़ना, न्यूनतम लागत, संतुलित लाभ, आदि) बहुत तेजी से काम करते हैं क्योंकि वे केवल एक संभव समाधान पर विचार करते हैं। ये विधियां इतनी तेजी से काम करती हैं कि कभी-कभी यह बदले में उन सभी को निष्पादित करने के लिए समझ में आता है, और फिर प्राप्त किए गए तीन समाधानों में से सर्वश्रेष्ठ का चयन करें। बेशक, यह गारंटी देना असंभव है कि यह समाधान सबसे अच्छा होगा, लेकिन यह निश्चित रूप से काफी अच्छा होगा।