🙌 💱 👋🏿 बाइक्यूबिक प्रक्षेप, सिद्धांत और व्यावहारिक कार्यान्वयन 👩🏾‍🎨 🚐 🤱🏿

2-आयामी मानचित्र पर कुछ मापों के परिणामों की कल्पना करने के लिए एक कार्य था, परिणाम क्रमशः एक समान ग्रिड पर नोडल बिंदुओं पर जाने जाते थे, क्रमशः कार्य प्राप्त डेटा के प्रक्षेप में कम हो गया था। मुख्य आवश्यकता थी - परिणामी छवि की गुणवत्ता और प्रक्षेप कलाकृतियों की न्यूनतम संख्या, इसलिए पसंद बायूबिक प्रक्षेप पर गिर गई। विकी लेख मुझे थोड़ा सूखा लग रहा था (कम से कम उस व्यक्ति के लिए जो स्कूल के बाद से गणित नहीं कर रहा था), लेकिन एल्गोरिथ्म का विवरण देने वाले एक भयानक लेख का लिंक भी था। यहां हम इस एल्गोरिथम के व्यावहारिक अनुप्रयोग पर विचार करेंगे और लेख का विश्लेषण करेंगे।

शब्दावली

इंटरपोलेशन, इंटरपोलेशन - कम्प्यूटेशनल गणित में, ज्ञात मूल्यों के उपलब्ध असतत सेट से मात्रा के मध्यवर्ती मूल्यों को खोजने का एक तरीका है।

घन प्रक्षेप

बाइबिक प्रक्षेप के सिद्धांत को बेहतर ढंग से समझने के लिए, मैं क्यूबिक प्रक्षेप के सिद्धांत पर विचार करने का प्रस्ताव करता हूं।

यदि फ़ंक्शन f (x) और इसके व्युत्पन्न के मानों को x = 0 और x = 1 बिंदुओं पर जाना जाता है, तो फ़ंक्शन को तीसरे क्रम के बहुपद का उपयोग करके अंतराल [0, 1] पर प्रक्षेपित किया जा सकता है। गणना के लिए सूत्र आसानी से प्राप्त किया जा सकता है।

तीसरा क्रम बहुपद और उसका व्युत्पन्न:

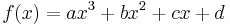
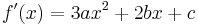
बहुपद के मान और उसके व्युत्पन्न बिंदु x = 0 और x = 1 पर

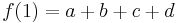
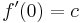
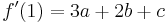
इन चार पहचान के रूप में लिखा जा सकता है:

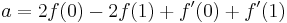
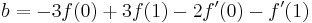
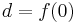
तो हमें अपना प्रक्षेप सूत्र मिला

व्यवहार में, एल्गोरिथ्म का उपयोग दिए गए बिंदुओं पर कुछ ज्ञात मूल्यों वाले कार्यों को प्रक्षेपित करने के लिए किया जाता है। इस मामले में, हम फ़ंक्शन के व्युत्पन्न को नहीं जान सकते हैं। हम दिए गए बिंदुओं पर व्युत्पन्न को 0 के रूप में ले सकते हैं, हालांकि, चिकनी और अधिक प्रशंसनीय फ़ंक्शन ग्राफ़ प्राप्त करने के लिए, हम व्युत्पन्न के रूप में पिछले और अगले बिंदुओं के बीच रेखा ढलान लेते हैं। इस प्रकार, गणना के लिए हमें 4 अंक चाहिए। मान लें कि हमारे पास x = -1, x = 0, x = 1 और x = 2 पर क्रमशः p0, p1, P2 और p3 में 4 फ़ंक्शन मान हैं। प्राप्त मानों को प्रतिस्थापित करें f (0), f (1), f (2) और f (3):

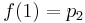
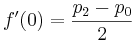
इन आंकड़ों की तुलना पहले प्राप्त सूत्रों से करें, हमारे पास है:

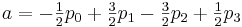
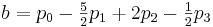
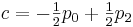
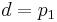
परिणाम:

PHP में इस एल्गोरिथ्म के कार्यान्वयन पर विचार करें:

/** *   * * @param array $p    : f(x0), f(x1), f(x2), f(x3) * @param float $x x-   * @return float   f($x) */ function cubicInterpolate ($p, $x) { return $p[1] + (-0.5 * $p[0] + 0.5 * $p[2]) * $x + ($p[0] - 2.5 * $p[1] + 2.0 * $p[2] - 0.5 * $p[3]) * $x * $x + (-0.5 * $p[0] + 1.5 * $p[1] - 1.5 * $p[2] + 0.5 * $p[3]) * $x * $x * $x; }

बाइक्यूबिक प्रक्षेप

बाइबिक प्रक्षेप दो आयामों में एक घन प्रक्षेप है। वास्तव में, हम अधिक आयामों में प्रक्षेप कर सकते हैं, लेकिन इस लेख के ढांचे के भीतर, हम केवल इस उदाहरण पर विचार करेंगे।
कल्पना कीजिए कि हम 16 अंक p _ij जानते हैं, जिसकी उत्पत्ति (i-1, j-1) के साथ होती है, जहाँ i, j 0 से 3 तक भिन्न होते हैं। फिर, हम क्षेत्र में सतह को प्रक्षेपित कर सकते हैं [0,0] x [ 1,1], इसके लिए हम 4 स्तंभों को प्रक्षेपित करते हैं और फिर प्राप्त परिणामों को क्षैतिज दिशा में प्रक्षेपित करते हैं:

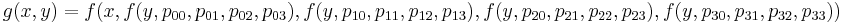
पहले समारोह के साथ संयुक्त PHP विधि कार्यान्वयन:

 /** *    * * @param array $p   2-  (4 x 4),    16-   * @param float $x x-   * @param float $y y-   * @return float   f($x, $y) */ function bicubicInterpolate ($p, $x, $y) { $tmp = array(); $tmp[0] = cubicInterpolate($p[0], $y); $tmp[1] = cubicInterpolate($p[1], $y); $tmp[2] = cubicInterpolate($p[2], $y); $tmp[3] = cubicInterpolate($p[3], $y); return cubicInterpolate($tmp, $x); }

सब कुछ बहुत अच्छा होगा, अगर एक समस्या के लिए नहीं - प्रदर्शन। डेटा की अपेक्षाकृत कम मात्रा को प्रक्षेपित करने के लिए गंभीर कंप्यूटिंग संसाधनों की आवश्यकता होती है। प्रदर्शन का अनुकूलन करने के लिए, निम्नलिखित दृष्टिकोण है।
बहुआयामी बहुपद के रूप में हमारे सूत्र पर विचार करें:

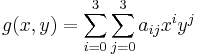
विस्तारित रूप में कुछ इस तरह होगा:

  g (x, y) = a00 * x ^ 0 * y ^ 0 + a01 * x ^ 0 * y ^ 1 + 
          a02 * x ^ 0 * y ^ 2 + a03 * x ^ 0 * y ^ 3 +
          a10 * x ^ 1 * y ^ 0 + a11 * x ^ 1 * y ^ 1 + 
          a12 * x ^ 1 * y ^ 2 + a13 * x ^ 1 * y ^ 3 +
          a20 * x ^ 2 * y ^ 0 + a21 * x ^ 2 * y ^ 1 + 
          a22 * x ^ 3 * y ^ 2 + a23 * x ^ 2 * y ^ 3 +
          a30 * x ^ 3 * y ^ 0 + a31 * x ^ 3 * y ^ 1 + 
          a32 * x ^ 3 * y ^ 2 + a33 * x ^ 3 * y ^ 3

अब आपको गुणांक एक _{आईजे की} गणना करने की आवश्यकता है। मैं विशेष रूप से यहां ध्यान देना चाहूंगा कि एक बार जब हम गुणांक की गणना करते हैं, तो हम उन्हें [0,0] से [1,1] तक अनुभाग में सभी मूल्यों को प्रक्षेपित करने के लिए उपयोग कर सकते हैं।

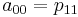
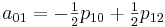
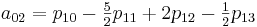
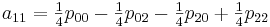
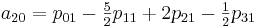
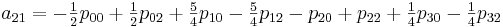
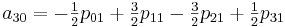
इस विधि को लागू करने के लिए, निम्न वर्ग बनाएं:

 class CachedBicubicInterpolator { private $a00, $a01, $a02, $a03, $a10, $a11, $a12, $a13, $a20, $a21, $a22, $a23, $a30, $a31, $a32, $a33; /** *  . * * @param array $p 2-  (4 x 4),      * @return void */ public function updateCoefficients ($p) { $this->a00 = $p[1][1]; $this->a01 = -.5 * $p[1][0] + .5 * $p[1][2]; $this->a02 = $p[1][0] - 2.5 * $p[1][1] + 2 * $p[1][2] - .5 * $p[1][3]; $this->a03 = -.5 * $p[1][0] + 1.5 * $p[1][1] - 1.5 * $p[1][2] + .5 * $p[1][3]; $this->a10 = -.5 * $p[0][1] + .5 * $p[2][1]; $this->a11 = .25 * $p[0][0] - .25 * $p[0][2] - .25 * $p[2][0] + .25 * $p[2][2]; $this->a12 = -.5 * $p[0][0] + 1.25 * $p[0][1] - $p[0][2] + .25 * $p[0][3] + .5 * $p[2][0] - 1.25 * $p[2][1] + $p[2][2] - .25 * $p[2][3]; $this->a13 = .25 * $p[0][0] - .75 * $p[0][1] + .75 * $p[0][2] - .25 * $p[0][3] - .25 * $p[2][0] + .75 * $p[2][1] - .75 * $p[2][2] + .25 * $p[2][3]; $this->a20 = $p[0][1] - 2.5 * $p[1][1] + 2 * $p[2][1] - .5 * $p[3][1]; $this->a21 = -.5 * $p[0][0] + .5 * $p[0][2] + 1.25 * $p[1][0] - 1.25 * $p[1][2] - $p[2][0] + $p[2][2] + .25 * $p[3][0] - .25 * $p[3][2]; $this->a22 = $p[0][0] - 2.5 * $p[0][1] + 2 * $p[0][2] - .5 * $p[0][3] - 2.5 * $p[1][0] + 6.25 * $p[1][1] - 5 * $p[1][2] + 1.25 * $p[1][3] + 2 * $p[2][0] - 5 * $p[2][1] + 4 * $p[2][2] - $p[2][3] - .5 * $p[3][0] + 1.25 * $p[3][1] - $p[3][2] + .25 * $p[3][3]; $this->a23 = -.5 * $p[0][0] + 1.5 * $p[0][1] - 1.5 * $p[0][2] + .5 * $p[0][3] + 1.25 * $p[1][0] - 3.75 * $p[1][1] + 3.75 * $p[1][2] - 1.25 * $p[1][3] - $p[2][0] + 3 * $p[2][1] - 3 * $p[2][2] + $p[2][3] + .25 * $p[3][0] - .75 * $p[3][1] + .75 * $p[3][2] - .25 * $p[3][3]; $this->a30 = -.5 * $p[0][1] + 1.5 * $p[1][1] - 1.5 * $p[2][1] + .5 * $p[3][1]; $this->a31 = .25 * $p[0][0] - .25 * $p[0][2] - .75 * $p[1][0] + .75 * $p[1][2] + .75 * $p[2][0] - .75 * $p[2][2] - .25 * $p[3][0] + .25 * $p[3][2]; $this->a32 = -.5 * $p[0][0] + 1.25 * $p[0][1] - $p[0][2] + .25 * $p[0][3] + 1.5 * $p[1][0] - 3.75 * $p[1][1] + 3 * $p[1][2] - .75 * $p[1][3] - 1.5 * $p[2][0] + 3.75 * $p[2][1] - 3 * $p[2][2] + .75 * $p[2][3] + .5 * $p[3][0] - 1.25 * $p[3][1] + $p[3][2] - .25 * $p[3][3]; $this->a33 = .25 * $p[0][0] - .75 * $p[0][1] + .75 * $p[0][2] - .25 * $p[0][3] - .75 * $p[1][0] + 2.25 * $p[1][1] - 2.25 * $p[1][2] + .75 * $p[1][3] + .75 * $p[2][0] - 2.25 * $p[2][1] + 2.25 * $p[2][2] - .75 * $p[2][3] - .25 * $p[3][0] + .75 * $p[3][1] - .75 * $p[3][2] + .25 * $p[3][3]; } /** *  . * * @param float $x $x = $x - $x0 * @param float $y $y = $y - $y0 * @return float    . */ public function getValue ($x, $y) { //   2  3 . $x2 = $x * $x; $x3 = $x2 * $x; $y2 = $y * $y; $y3 = $y2 * $y; return ($this->a00 + $this->a01 * $y + $this->a02 * $y2 + $this->a03 * $y3) + ($this->a10 + $this->a11 * $y + $this->a12 * $y2 + $this->a13 * $y3) * $x + ($this->a20 + $this->a21 * $y + $this->a22 * $y2 + $this->a23 * $y3) * $x2 + ($this->a30 + $this->a31 * $y + $this->a32 * $y2 + $this->a33 * $y3) * $x3; } }

व्यावहारिक अनुप्रयोग

निम्नलिखित उदाहरण में बाइबिक प्रक्षेप के उपयोग पर विचार करें:
स्रोत डेटा: डेटा सरणी 7 x 7 अंक
आवश्यकता है: सतह को 300 x 300 पिक्सेल की छवि के रूप में प्रस्तुत करें।

मैंने कोड में प्रत्येक चरण पर टिप्पणी करने की यथासंभव कोशिश की, मुझे लगता है कि सब कुछ स्पष्ट होगा

 <?php header("Content-type: image/png");//  include 'interpolation.php';//   include 'colormap.php';//   $simpleData = array( array(0, 0.1, 0.15, 0.2, 0.15, 0.1, 0), array(0, 0.1, 0.5, 1, 0.9, 0.1, 0), array(0, 0.1, 0.7, 1, 0.9, 0.1, 0), array(0, 0.1, 0.6, 0.7, 0.5, 0.1, 0), array(0, 0.2, 0.8, 0.6, 0.15, 0.08, 0.1), array(0.08, 0.2, 0.15, 0.2, 0.15, 0.1, 0.1), array(0.1, 0.8, 0.1, 0.1, 0.1, 0, 0) );//    7  7 $countX = count($simpleData[0]);//    $countY = count($simpleData); $input = array(); /*       *      ,         *     -      */ for ($i = 0; $i < $countX; $i ++) { for ($j = 0; $j < $countY; $j ++) { $input[$i + 1][$j + 1] = $simpleData[$j][$i]; if ($i == 0) { $input[0][$j + 1] = $simpleData[$j][$i] - $simpleData[$j][$i + 1];//  } if ($i == ($countX - 1)) { $input[$countX + 1][$j + 1] = $simpleData[$j][$i] - $simpleData[$j][$i - 1];//  } if ($j == 0) { $input[$i + 1][0] = $simpleData[$j][$i] - $simpleData[$j + 1][$i];//  } if ($j == ($countY - 1)) { $input[$i + 1][$countY + 1] = $simpleData[$j][$i] - $simpleData[$j - 1][$i];//  } } } /*   *     ,     . */ $input[0][0] = ($input[1][0] + $input[0][1]) / 2; $input[$countX + 1][0] = ($input[$countX][0] + $input[$countX][1]) / 2; $input[0][$countY + 1] = ($input[0][$countY] + $input[1][$countY]) / 2; $input[$countX + 1][$countY + 1] = ($input[$countX + 1][$countY] + $input[$countX][$countY]) / 2; $step = 50; //  50  $img = imagecreatetruecolor(($countX - 1) * $step, ($countY - 1) * $step);//    $colormap = createColormap($img);//   $b2i = new CachedBicubicInterpolator(); for ($i = 1; $i < $countX; $i ++) {//   for ($j = 1; $j < $countY; $j ++) { $points = array(); $points[0][0] = $input[$i - 1][$j - 1]; $points[1][0] = $input[$i][$j - 1]; $points[2][0] = $input[$i + 1][$j - 1]; $points[3][0] = $input[$i + 2][$j - 1]; $points[0][1] = $input[$i - 1][$j]; $points[1][1] = $input[$i][$j]; $points[2][1] = $input[$i + 1][$j]; $points[3][1] = $input[$i + 2][$j]; $points[0][2] = $input[$i - 1][$j + 1]; $points[1][2] = $input[$i][$j + 1]; $points[2][2] = $input[$i + 1][$j + 1]; $points[3][2] = $input[$i + 2][$j + 1]; $points[0][3] = $input[$i - 1][$j + 2]; $points[1][3] = $input[$i][$j + 2]; $points[2][3] = $input[$i + 1][$j + 2]; $points[3][3] = $input[$i + 2][$j + 2]; $b2i->updateCoefficients($points);//  for ($x = 0; $x < $step; $x ++) {//   for ($y = 0; $y < $step; $y ++) { $rx = ($i - 1) * $step + $x;//     $ry = ($j - 1) * $step + $y;//y     $ax = $x / $step;//x - x0 $ay = $y / $step;//y - y0 $val = $b2i->getValue($ax, $ay);//  $color = ceil(($val) * 1024) - 1;//  if ($color < 0) $color = 0;//   if ($color > 1023) $color = 1023;//   imagesetpixel($img, $rx, $ry, $colormap[$color]);//  } } } } imagepng($img); ?>

रंग मानचित्र बनाने के लिए अलग से प्रदान की गई फ़ाइल

 function createColormap(&$image) { $colormap = array(); for ($i = 0; $i < 256; $i ++) { $colormap[$i] = imagecolorallocate($image, 0, $i, 255); } for ($i = 0; $i < 256; $i ++) { $colormap[$i + 256] = imagecolorallocate($image, 0, 255, 255 - $i); } for ($i = 0; $i < 256; $i ++) { $colormap[$i + 512] = imagecolorallocate($image, $i, 255, 0); } for ($i = 0; $i < 256; $i ++) { $colormap[$i + 768] = imagecolorallocate($image, 255, 255 - $i, 0); } return $colormap; }

बाइक्यूबिक प्रक्षेप, सिद्धांत और व्यावहारिक कार्यान्वयन

शब्दावली

घन प्रक्षेप

बाइक्यूबिक प्रक्षेप

व्यावहारिक अनुप्रयोग

काम का परिणाम:

More articles: