अपने काम में, सिग्नल में हार्मोनिक घटकों की उपस्थिति को जल्दी से निर्धारित करने की आवश्यकता के साथ उन्हें बार-बार सामना करना पड़ा। अक्सर, अनुमानित अनुमान के लिए, यह तेजी से फूरियर रूपांतरण का उपयोग करने के लिए पर्याप्त है। इसके अलावा, इसका कार्यान्वयन लगभग सभी गणितीय पैकेजों और पुस्तकालयों में है, और इसे व्यक्तिगत रूप से लागू करना मुश्किल नहीं होगा। इस बीच, अनुभव से पता चलता है कि, इसकी सभी सादगी के साथ, विधि कुछ प्रश्न उठाने लगती है जब यह आवश्यक नहीं हो जाता है कि एक संकेत में असतत नमूनों की उपस्थिति को देखें, बल्कि उनके पूर्ण मूल्यों का पता लगाने के लिए, अर्थात्। परिणाम को सामान्य करें।
इस लेख में मैं समझाने की कोशिश करूंगा कि क्या, फिर भी, MATLAB का उपयोग करके परिणाम के रूप में fft (फास्ट फूरियर ट्रांसफॉर्म) पैदा करता है (और एक बोनस के रूप में मैं इस बहुत उपयोगी भाषा पर एक छोटा शैक्षिक कार्यक्रम आयोजित करूंगा, मेरी राय में)।
MATLAB आपको अनावश्यक वस्तुओं के मैनुअल हटाने से परेशान नहीं होने देता है, हालांकि, जब अधिक या कम मात्रा में डेटा सरणियों के साथ काम करते हैं, तो उन्हें टोपीदार होने और स्मृति की कमी के बारे में शिकायत करने की आदत होती है। मेमोरी को साफ़ करने के लिए, हटाए जाने वाले ऑब्जेक्ट के नाम के साथ स्पष्ट प्रक्रिया का उपयोग करें।
यह वह जगह है जहाँ हम शुरू करते हैं। चूँकि हम अपनी ज़रूरत की हर चीज़ को खुद ही पैदा करेंगे, इसलिए हम एक सक्रिय सत्र के दौरान कार्यक्षेत्र में जमा हुई सभी चीज़ों को सुरक्षित रूप से हटा सकते हैं।
clear all%तो, सबसे पहले, हम अपने मॉडल के लिए प्रारंभिक डेटा सेट करेंगे। फूरियर विश्लेषण हस्तक्षेप से हार्मोनिक संकेतों को निकालने के लिए आदर्श है। इसे प्रदर्शित करने के लिए, हम संकेत के रूप में एक निश्चित स्थिर और दो साइनसोइड्स को विभिन्न आवृत्तियों और आयामों के साथ लेते हैं। शोर फैलाव पहले साइनसॉइड के आयाम का 3 गुना है। हम आवृत्ति बैंड की संख्या भी निर्धारित करते हैं जिसे एफटीपी एल्गोरिदम को गणना करना चाहिए। लाइनों के अंत में एक अर्धविराम वैकल्पिक है, और यदि आप इसे नहीं डालते हैं, तो फ़ंक्शन और सेटिंग चर की गणना के परिणाम को कमांड लाइन में डुप्लिकेट किया जाएगा, जिसका उपयोग कोड को डीबग करने के लिए किया जा सकता है (हालांकि, कमांड लाइन पर एक ठोस कैनवास के साथ 512 मान आपकी मदद करने की संभावना नहीं है, विशेष रूप से उनके उत्पादन में भी कुछ समय लगता है, इसलिए बेहतर है कि लाइनों को बंद न करें)।
%%
Tm=5;% ()
Fd=512;% ()
Ak=0.5;% ()
A1=1;% ()
A2=0.7;% ()
F1=13;% ()
F2=42;% ()
Phi1=0;% ()
Phi2=37;% ()
An=3*A1;% ()
FftL=1024;%
MATLAB (मैट्रिक्स प्रयोगशाला), जैसा कि नाम से पता चलता है, मुख्य रूप से सरणियों के साथ काम करने के लिए डिज़ाइन किया गया है, इसमें लगभग सभी गणना एल्गोरिदम वैक्टर के साथ काम करने के लिए अनुकूलित हैं। सुविधाजनक काम के साधनों की बहुतायत भी कई स्रोतों के रूप में मौजूद डेटा को मैट्रीस के रूप में प्रस्तुत करने के लिए विनीत है। विशेष रूप से, कोई व्यक्ति दिए गए चरण के साथ आसानी से बढ़ती (घटती) मात्रा का एक सरणी उत्पन्न कर सकता है (इस उदाहरण में 1 \ Fd):
%%
T=0:1/Fd:Tm;%
रैंडम समारोह द्वारा यादृच्छिक गाऊसी शोर निर्धारित किया जाता है, जिसके परिणामस्वरूप इसके मापदंडों में निर्दिष्ट आयाम की एक सरणी होती है। एकरूपता के लिए, हम इसे एक स्ट्रिंग (पहले पैरामीटर 1) के रूप में परिभाषित करते हैं, जो हमारे समय के नमूने की लंबाई के अनुरूप लंबाई है, जो कि लंबाई फ़ंक्शन द्वारा गणना की जाती है।
Noise=An*randn(1,length(T));%गुणन को इंगित करने के लिए प्रतीक * का उपयोग किया जाता है। क्योंकि सबसे अधिक बार वैक्टर पर कार्रवाई की जाती है, फिर गुणन वेक्टर द्वारा निहित होता है, लेकिन यह आसानी से संभव है, इस ऑपरेटर को ओवरलोड किए बिना, इसके सामने डॉट (। *) जोड़कर तात्कालिक रूप से गुणा करने के लिए। जब एक वेक्टर को स्केलर से गुणा किया जाता है, तो गुणन से पहले बिंदु वैकल्पिक होता है। इसके अलावा, जोड़ा डॉट वृद्धिशील और विभाजन तत्व-दर-तत्व बना देगा।
Signal=Ak+A1*sind((F1*360).*T+Phi1)+A2*sind((F2*360).*T+Phi2);% ( 2 )अब इस उद्देश्य के लिए आगे बढ़ते हैं, जिस पर इस लेख की कल्पना की गई थी - एफएफटी () फ़ंक्शन। मानक MATLAB फ़ंक्शन की दलीलें स्वयं सिग्नल हैं (हमारे मामले में, सिग्नल), परिणाम वेक्टर के आयाम (एफएफटीएल), साथ ही साथ माप भी।
आखिरी तर्क यह निर्धारित करता है कि सिग्नल किस आयाम पर स्थित है यदि इनपुट के लिए एक बहुआयामी सरणी दिया जाता है (कभी-कभी यह पैरामीटर फूरियर रूपांतरण के आयाम के लिए गलत होता है, लेकिन ऐसा नहीं है। हालांकि MATLAB में 2-आयामी fft2 () और बहुआयामी fftn () एल्गोरिदम) के कार्यान्वयन हैं। । चूंकि हमारा सिग्नल एक वेक्टर है, इसलिए इसे पूरी तरह से छोड़ा जा सकता है।
हम पहले शोर के एक प्रवेश के बिना एक संकेत पर विचार करते हैं। नतीजतन, हम जटिल संख्याओं का एक वेक्टर प्राप्त करते हैं। यह घातीय रूप में आवृत्ति डोमेन में हमारे सिग्नल का प्रतिनिधित्व है। यानी इन जटिल संख्याओं के मॉड्यूल संबंधित आवृत्तियों के आयामों का प्रतिनिधित्व करते हैं (अधिक सटीक, आवृत्ति बैंड नीचे देखते हैं), और तर्क उनके प्रारंभिक चरण हैं। और यदि प्राप्त चरण को रेडियंस में स्पष्ट रूप से गणना की जाती है, तो आयाम और आवृत्तियों के साथ यह इतना सरल नहीं है।
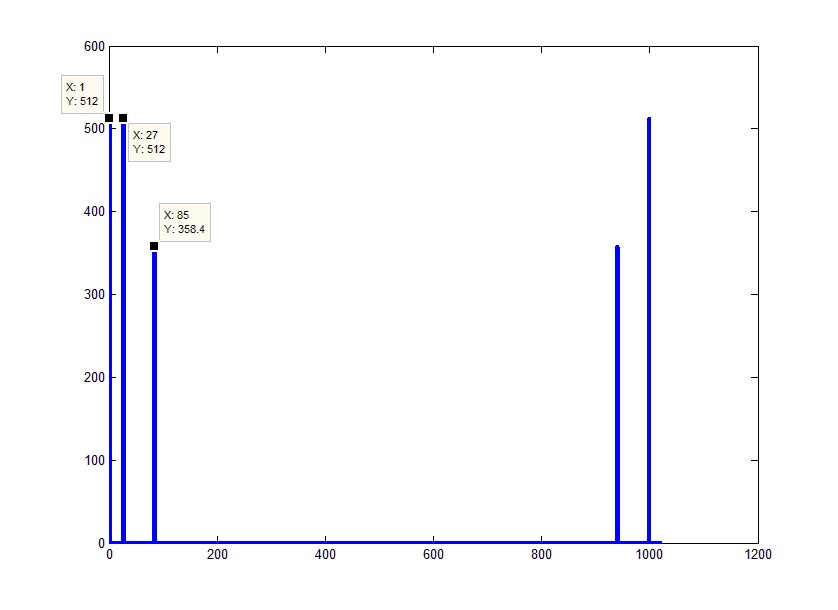
उदाहरण के लिए, यदि हम अपने सिग्नल में फूरियर ट्रांसफॉर्म को लागू करते हैं, और आउटपुट में वेक्टर के पूर्ण मूल्यों को लेते हैं, तो हमें निम्नलिखित चित्र मिलते हैं:
द्वि-आयामी ग्राफ़ बनाने के लिए, प्लॉट फ़ंक्शन का उपयोग करना सुविधाजनक है। इस फ़ंक्शन में उपयोग किए जाने वाले मुख्य पैरामीटर बिंदुओं के एक-आयामी एरे हैं, पहला ऑर्डिनेट अक्ष सेट करता है, और दूसरा संबंधित बिंदुओं पर फ़ंक्शन मान सेट करता है। यदि आप केवल एक सरणी पास करते हैं, तो इसे 1 के निश्चित चरण के साथ प्रदर्शित किया जाएगा।
यदि आप परिणामी तस्वीर को करीब से देखते हैं, तो यह पता चलता है कि यह हमारी अपेक्षाओं से कुछ अलग है। नीचे दिए गए ग्राफ़ में, अपेक्षित 3x (निरंतर + 2 साइनसोइड्स) के बजाय 5 चोटियां हैं, उनके एम्पलीट्यूड मूल संकेतों के आयामों के साथ मेल नहीं खाते हैं, और एब्सिस्सा अक्ष शायद ही आवृत्तियों को दर्शाता है।
सबसे पहले, यह ध्यान में रखा जाना चाहिए कि एल्गोरिथ्म स्कोर इस तरह से डिज़ाइन किया गया है कि न केवल सकारात्मक, बल्कि नकारात्मक आवृत्तियों को भी हल किया जाता है और ग्राफ़ के दाईं ओर वास्तविक स्पेक्ट्रम का "दर्पण" प्रदर्शन होता है। यानी वास्तव में, 0 (जो सिग्नल के निरंतर भाग से मेल खाती है) सरणी के बीच में होना चाहिए। सरणी की आधी लंबाई से चक्रीय बदलाव करके स्थिति को ठीक किया जा सकता है। इन उद्देश्यों के लिए, MATLAB में शिफ्ट फ़ंक्शन fftshift () है जो पहले तत्व को सरणी के मध्य में स्थानांतरित करता है:
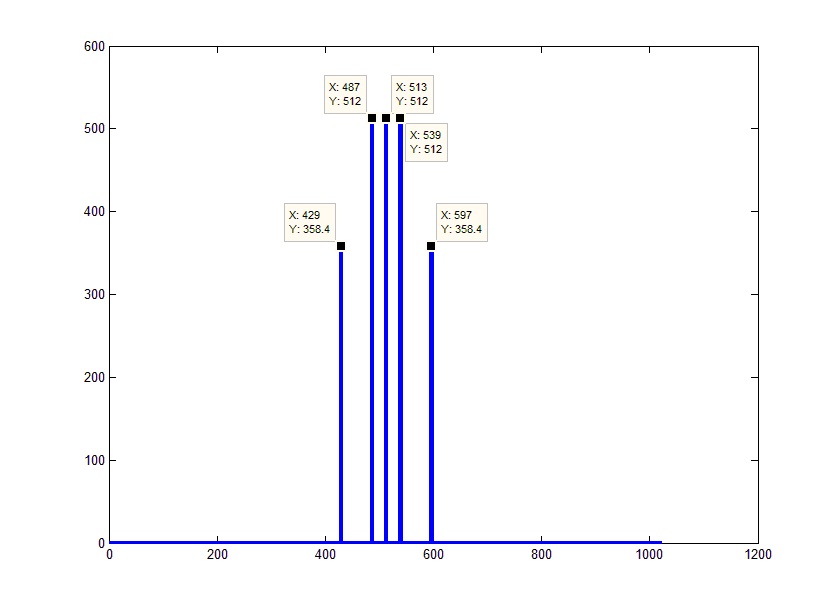
अब मानों की धुरी पर ध्यान दें।
नमूना प्रमेय के अनुसार (इसे न्यक्विस्ट-शैनन प्रमेय या अधिक देशभक्ति केटलनिकोव प्रमेय के रूप में भी जाना जाता है) के अनुसार, असतत संकेत का स्पेक्ट्रम आधा नमूना आवृत्ति (एफडी) तक सीमित होगा। या हमारे मामले में -Fd / 2 बाईं ओर और Fd / 2 दाईं ओर। यानी संपूर्ण परिणामी सरणी Fd आवृत्तियों को कवर करती है। यहाँ से, इस बात को ध्यान में रखते हुए कि हम जानते हैं (या बल्कि स्वतंत्र रूप से पैरामीटर को पैरामीटर के रूप में सेट करते हैं) सरणी की लंबाई, हम मानों की एक सरणी के रूप में आवृत्तियों को प्राप्त करते हैं - Fd / 2 से Fd / 2 तक Fd / FftL के वेतन वृद्धि में (वास्तव में, सही आवृत्ति एक सीमा से कम होगी गिनती यानी एफडी / 2-एफडी / एफएफटीएल):
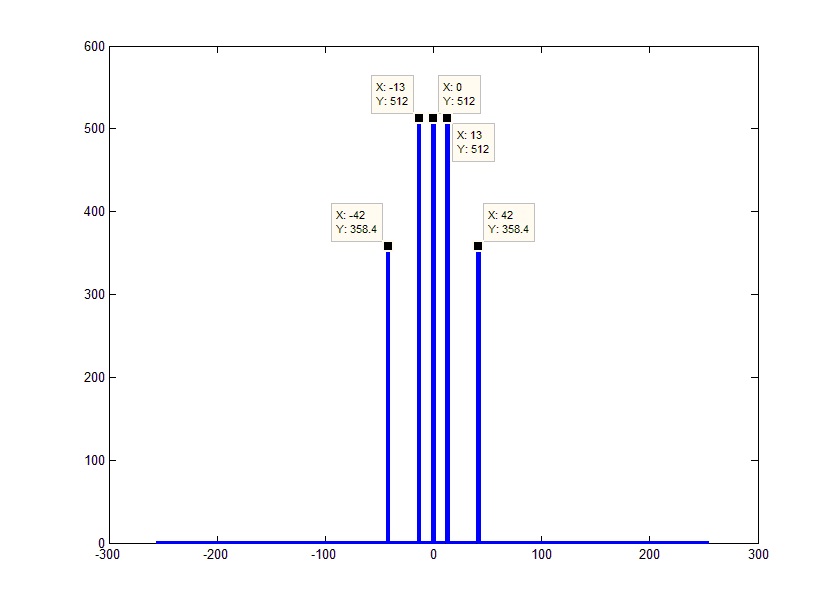
यदि आप आवृत्तियों के चरणों को देखते हैं, तो आप देख सकते हैं कि वे इसी नकारात्मक आवृत्तियों के नकारात्मक चरणों के बराबर हैं। स्पेक्ट्रम के बाएं और दाएं हिस्सों के आयामों और उनके चरणों के पत्राचार की समानता को देखते हुए, पूरे स्पेक्ट्रम दोगुने आयाम के साथ अपने सकारात्मक हिस्से के बराबर होगा। अपवाद केवल 0 तत्व है, जिसमें दर्पण आधा नहीं है। इस प्रकार, "असंगत" और अक्सर अनावश्यक नकारात्मक आवृत्तियों से छुटकारा पाना संभव है। यह मूल सरणी के अंत को त्यागकर और शेष तत्वों को 2 से गुणा करके (स्थिर घटक को छोड़कर) तुरंत किया जा सकता है:
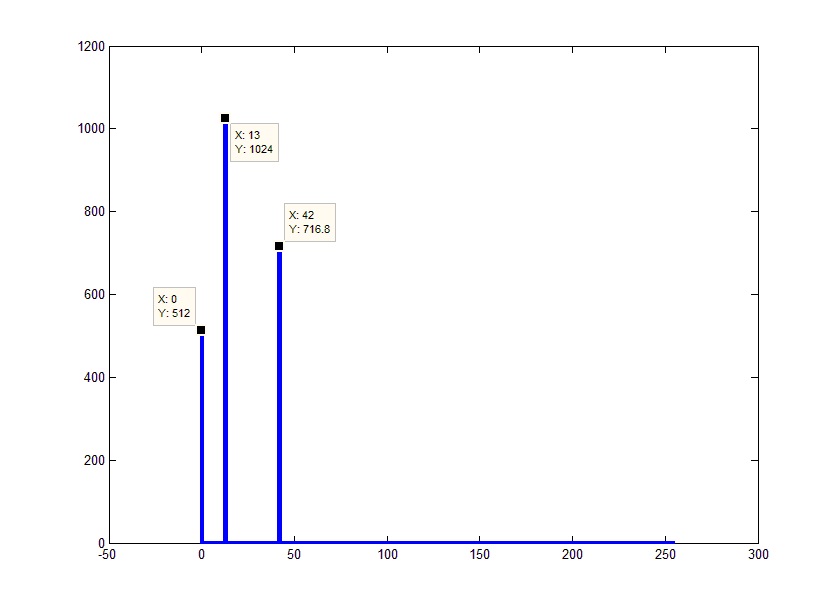
अब यह पहले से ही परिणाम के समान है जो हम उम्मीद करते हैं। केवल एक चीज जो अब परेशान है। इसके साथ, सब कुछ काफी सरल है। क्योंकि चूंकि तेजी से फूरियर ट्रांसफॉर्म वास्तव में प्रत्येक आवृत्ति के लिए ट्रांसफ़ॉर्मेशन कोर (कॉम्प्लेक्स एक्सपोनेंट) द्वारा गुणा किए गए सिग्नल का एक सारांश है, वास्तविक परिणाम रकम की संख्या (परिणाम के रूप में आवृत्तियों) में प्राप्त परिणाम से कम होगा, अर्थात। परिणाम को परिणाम में तत्वों की संख्या से विभाजित किया जाना चाहिए (यह मत भूलो कि परिणाम पूरे उत्तर है, एक साथ छोड़े गए भाग के साथ, यानी हमारे दिए गए एफएफटीएल):
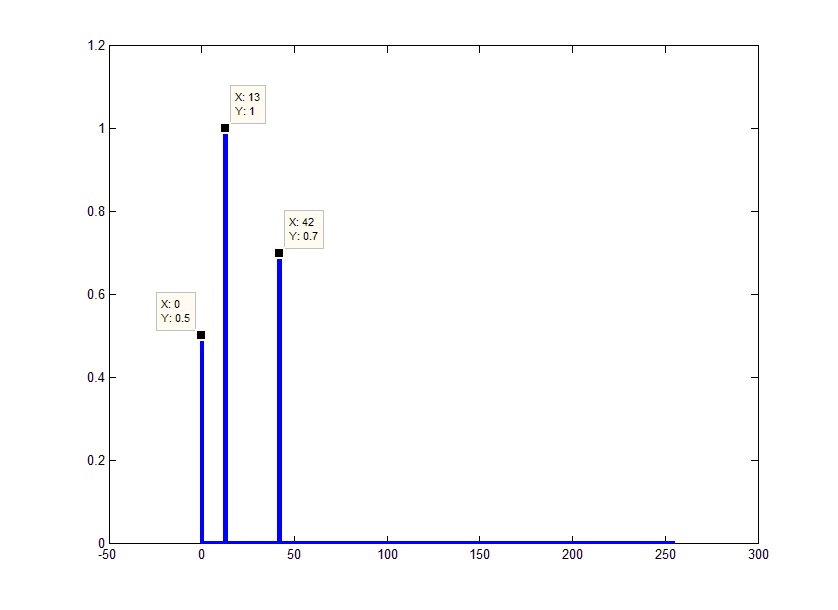
एक और बात ध्यान देने योग्य है। वर्णक्रमीय प्रतिनिधित्व में, यह उस आवृत्ति पर सिग्नल मूल्य नहीं है जो एल्गोरिथ्म हिट है कि गणना की जाती है (जैसा कि हम याद करते हैं, फ्रीक्वेंसी एफडी / एफएफटीएल के वेतन वृद्धि में अनुसरण करते हैं), लेकिन बैंड में मूल्य (कदम की चौड़ाई के बराबर)। यानी यदि कई नमूने इस बैंड में आते हैं, तो उन्हें जोड़ दिया जाता है। उदाहरण के लिए, आप एल्गोरिथ्म के परिणामस्वरूप लाइनों की संख्या को कम कर सकते हैं:
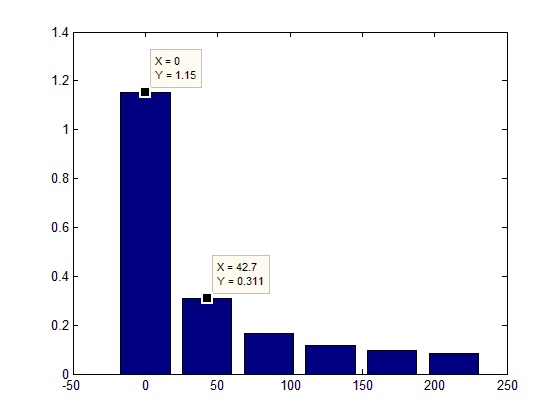
हालांकि, इसका मतलब यह नहीं है कि यह तुरंत काम की सटीकता को बढ़ाने के तुरंत विचार के लायक है, क्योंकि यह भी नकारात्मक परिणामों की ओर जाता है, क्योंकि यदि रिज़ॉल्यूशन सिग्नल की नमूना आवृत्ति के साथ तुलनीय है, तो "विंडो" के हार्मोनिक्स स्पेक्ट्रम में जाएंगे, जो वास्तविक सिग्नल से संबंधित नहीं हैं, लेकिन इसके असतत प्रतिनिधित्व से संबंधित हैं:
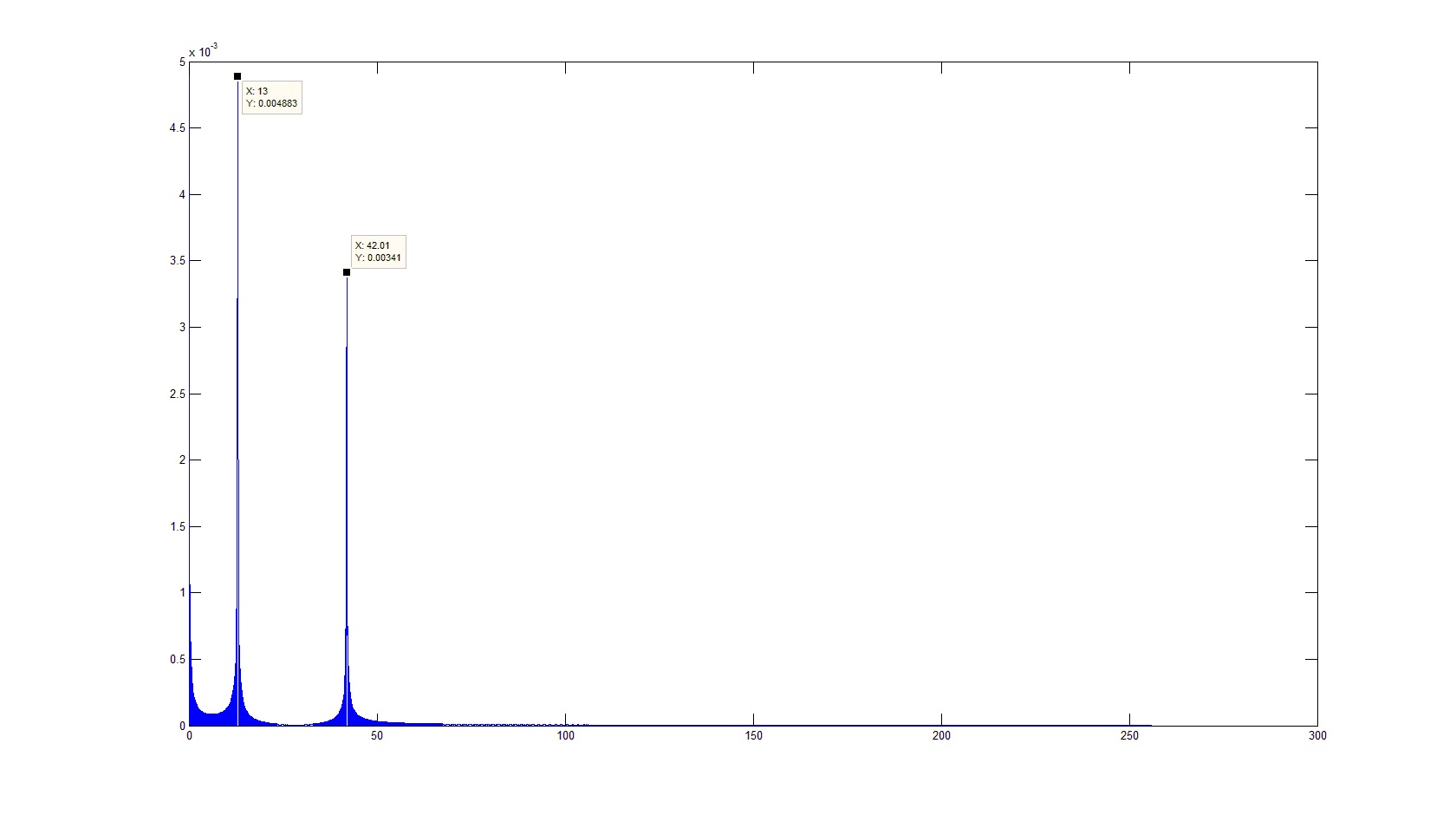
या अधिक बारीकी से एक विचारशील के पड़ोस:
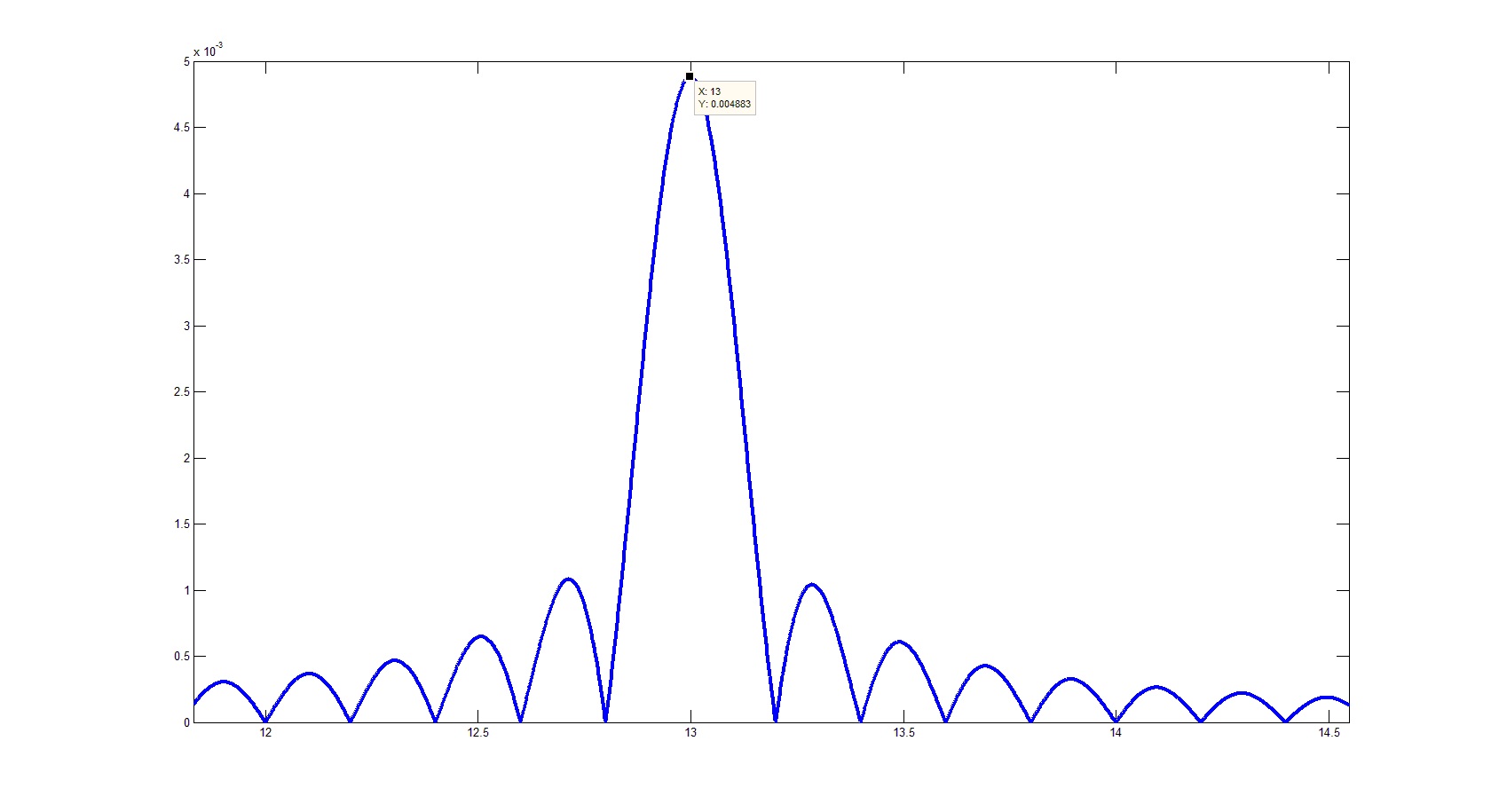
Fft को सामान्य करने का कोड कुछ इस तरह दिखेगा:
%%
FftS=abs(fft(Signal,FftL));%
FftS=2*FftS./FftL;%
FftS(1)=FftS(1)/2;%
FftSh=abs(fft(Signal+Noise,FftL));% +
FftSh=2*FftSh./FftL;%
FftSh(1)=FftSh(1)/2;%
हमें केवल परिणामों को आउटपुट करने की आवश्यकता है। सबप्लोट फ़ंक्शन आपको ग्राफ़ प्रदर्शित करने के लिए कई क्षेत्रों में विंडो को विभाजित करने की अनुमति देता है।
%%
subplot(2,1,1);%
plot(T,Signal);%
title('');%
xlabel(' ()');%
ylabel(' ()');%
subplot(2,1,2);%
plot(T,Signal+Noise);% +
title('+');%
xlabel(' ()');%
ylabel(' ()');%
F=0:Fd/FftL:Fd/2-1/FftL;%
figure%
subplot(2,1,1);%
plot(F,FftS(1:length(F)));%
title(' ');%
xlabel(' ()');%
ylabel(' ()');%
subplot(2,1,2);%
plot(F,FftSh(1:length(F)));%
title(' ');%
xlabel(' ()');%
ylabel(' ()');%
कोड निष्पादन का परिणाम इस तरह दिखाई देगा:
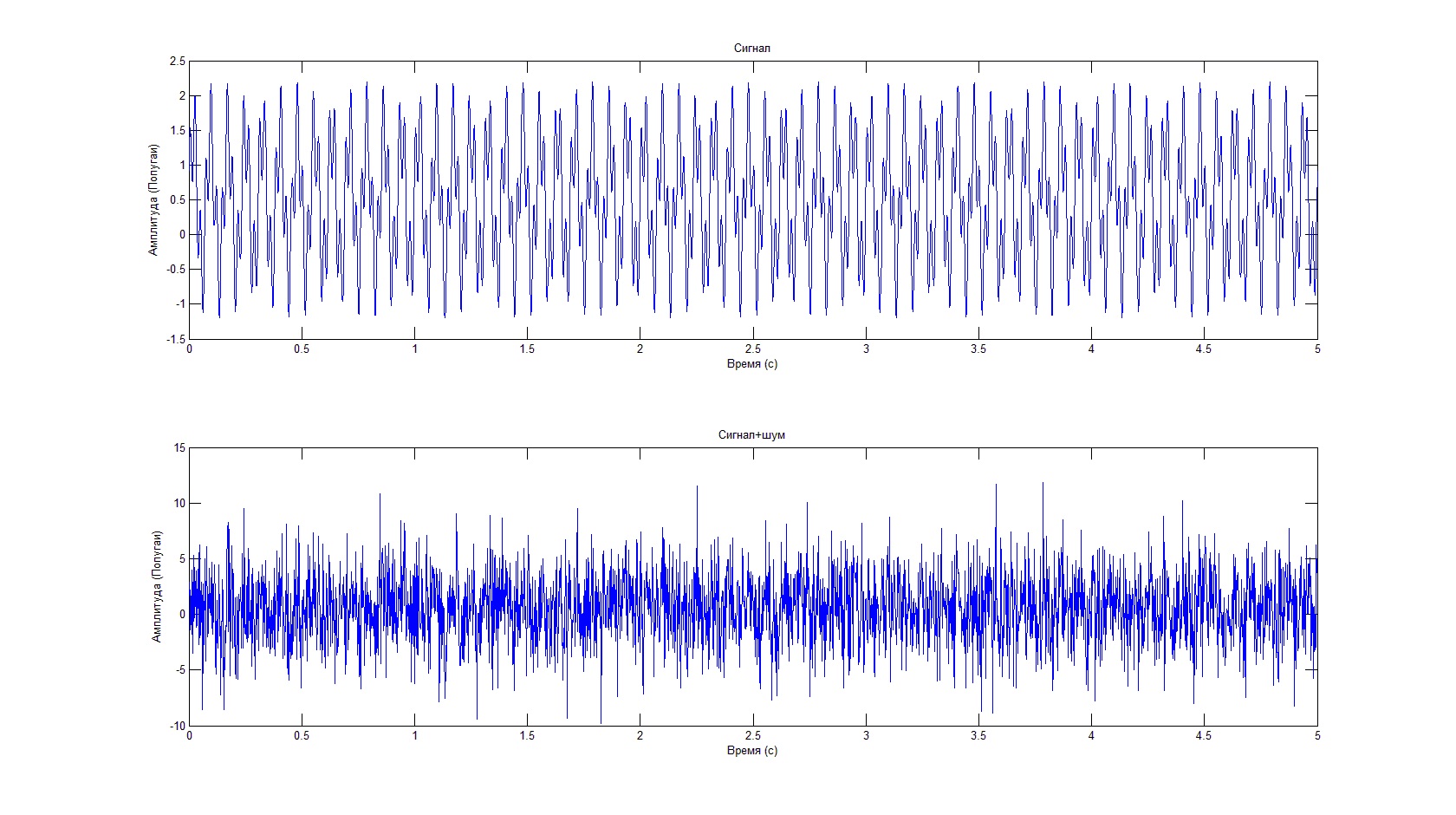
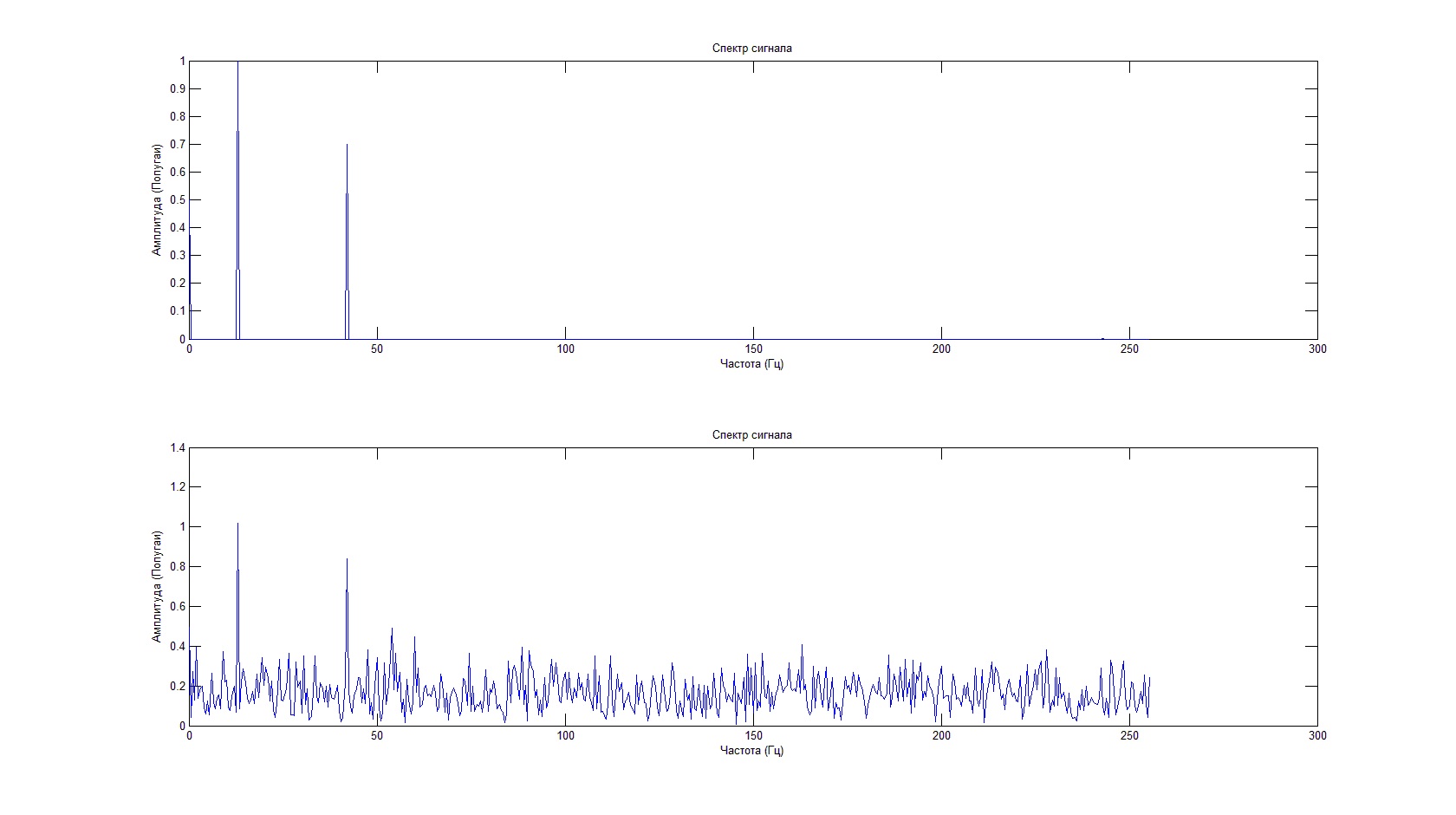
इस तथ्य के बावजूद कि शोर की पृष्ठभूमि के खिलाफ उपयोगी संकेत दिखाई नहीं देता है, वर्णक्रमीय विशेषता इसकी आवृत्ति और आयाम को निर्धारित करने की अनुमति देती है।
मुझे आशा है कि यह पाठ आपके लिए उपयोगी था।