पदार्थ खोज और संबंधित मामले

नमस्कार प्रिय समुदाय! हाल ही में Habré पर एक अच्छे समीक्षा लेख ने स्ट्रिंग में एक विकल्प के लिए अलग-अलग खोज एल्गोरिदम के बारे में पर्ची की। दुर्भाग्य से, उल्लिखित एल्गोरिदम में से किसी का कोई विस्तृत विवरण नहीं था। मैंने इस अंतर को भरने का फैसला किया और कम से कम उन लोगों के बारे में बताया जो संभवतः याद किए जा सकते हैं। जो लोग अभी भी संस्थान से एल्गोरिदम के पाठ्यक्रम को याद करते हैं, वे शायद अपने लिए कुछ नया नहीं पाएंगे।

सबसे पहले, मैं इस सवाल को रोकना चाहूंगा कि "आखिर यह क्यों है?" सब कुछ पहले से ही लिखा है। ” हाँ, यह लिखा है। लेकिन सबसे पहले, यह जानना उपयोगी है कि आप जिन उपकरणों का उपयोग करते हैं, वे निचले स्तर पर अपनी सीमाओं को बेहतर ढंग से समझने के लिए काम करते हैं, और दूसरी बात यह है कि बड़े आसन्न क्षेत्र हैं जहां बॉक्स से काम करने वाले स्ट्रैस () फ़ंक्शन पर्याप्त नहीं हैं। अच्छी तरह से और तीसरे, आप अशुभ हो सकते हैं और मोबाइल प्लेटफॉर्म के लिए एक रनटाइम विकसित करना होगा, और फिर यह जानना बेहतर होगा कि आप क्या कर रहे हैं यदि आप इसे पूरक करने का निर्णय लेते हैं (यह सुनिश्चित करने के लिए कि यह एक वैक्यूम में गोलाकार समस्या नहीं है, तो बस wcslen () का प्रयास करें) wcsstr () Android NDK से)।

लेकिन क्या वास्तव में खोज करना असंभव है?

तथ्य यह है कि स्पष्ट तरीका, जो सब कुछ "ले और खोज" के रूप में तैयार करता है, किसी भी तरह से सबसे प्रभावी नहीं है, और इस तरह के निम्न-स्तर और अपेक्षाकृत अक्सर फ़ंक्शन के लिए, यह महत्वपूर्ण है। तो, योजना यह है:

1. समस्या कथन: परिभाषाएँ और रूढ़ियाँ यहाँ सूचीबद्ध हैं।
2. निर्णय "माथे पर": यहां यह वर्णित किया जाएगा कि यह कैसे करना है और क्यों नहीं।
3. जेड-फ़ंक्शन: प्रतिस्थापन खोज के सही कार्यान्वयन का सबसे सरल संस्करण।
4. नूथ-मॉरिस-प्रैट एल्गोरिथम: एक और सही खोज विकल्प।
5. अन्य खोज कार्य: विस्तृत विवरण के बिना संक्षेप में उन पर जाएं।
   

समस्या का बयान

समस्या का विहित संस्करण इस तरह दिखता है: हमारे पास लाइन ए ( पाठ ) है। यह जांचना आवश्यक है कि क्या इसमें एक विकल्प X (एक पैटर्न ) है, और यदि हां, तो यह कहां से शुरू होता है। यही स्ट्रैट () फ़ंक्शन सी में करता है। इसके अलावा, आप पैटर्न की सभी घटनाओं को खोजने के लिए भी कह सकते हैं। जाहिर है, कार्य केवल तभी समझ में आता है जब एक्स ए की तुलना में नहीं है ।
आगे की व्याख्या की सादगी के लिए, मैं एक बार में कुछ अवधारणाओं को पेश करूंगा। एक स्ट्रिंग क्या है, हर कोई शायद समझता है - यह पात्रों का एक क्रम है, संभवतः खाली है। प्रतीक , या अक्षर, एक निश्चित सेट से संबंधित होते हैं, जिसे वर्णमाला कहा जाता है (यह वर्णमाला, आम तौर पर बोलना, सामान्य ज्ञान में वर्णमाला से कोई लेना-देना नहीं हो सकता है)। स्ट्रिंग की लंबाई | ए | - यह स्पष्ट रूप से इसमें पात्रों की संख्या है। स्ट्रिंग A [ ..i ] का उपसर्ग स्ट्रिंग A के पहले i अक्षर का स्ट्रिंग है । स्ट्रिंग का प्रत्यय A [ j .. ] स्ट्रिंग है | A - -j + 1 अंतिम वर्ण A से प्रतिस्थापन को A [ i..j ] के रूप में दर्शाया जाएगा, और A [ i ] स्ट्रिंग का i-th वर्ण है। खाली प्रत्यय और उपसर्ग, आदि के बारे में प्रश्न स्पर्श न करें - स्थानीय रूप से उनसे निपटना मुश्किल नहीं है। अभी भी प्रहरी के रूप में ऐसी चीज है - एक अद्वितीय प्रतीक जो वर्णमाला में नहीं पाया जाता है। यह $ प्रतीक द्वारा दर्शाया गया है और इस तरह के प्रतीक के साथ एक वैध वर्णमाला द्वारा पूरक है (सिद्धांत रूप में, व्यवहार में अतिरिक्त प्रतीकों को लागू करना आसान है जो कि इनपुट लाइनों में प्रकट नहीं हो सकता है)।
गणनाओं में, हम पहली स्थिति से स्ट्रिंग में वर्णों पर विचार करेंगे। शून्य से गिनती करके कोड लिखना पारंपरिक रूप से आसान है। एक से दूसरे में संक्रमण मुश्किल नहीं है।

माथे का घोल

प्रत्यक्ष खोज, या, जैसा कि वे अक्सर कहते हैं, "बस उठाओ और खोज," पहला समाधान है जो एक अनुभवहीन व्यायामी के दिमाग में आता है। सार सरल है: स्ट्रिंग ए के साथ जाने के लिए जाँच की जाए और उसमें वांछित स्ट्रिंग एक्स के पहले चरित्र की घटना के लिए देखें। जब हम पाते हैं, हम परिकल्पना करते हैं कि यह एक ही वांछित प्रविष्टि है। फिर यह लाइन ए के संगत पात्रों के साथ मिलान के लिए टेम्पलेट के सभी बाद के पात्रों को बारी-बारी से जांचता रहता है । यदि वे सभी मेल खाते हैं, तो यह हमारे सामने है। लेकिन यदि कोई एक पात्र मेल नहीं खाता है, तो हमारी परिकल्पना को असत्य के रूप में पहचानने के अलावा कुछ भी नहीं रहता है, जो हमें X से पहले चरित्र की घटना के बाद चरित्र में लौटता है।
कई लोग इस बिंदु पर गलत हैं, यह मानते हुए कि वापस जाने के लिए आवश्यक नहीं है, लेकिन आप मौजूदा स्थिति से प्रसंस्करण ए को जारी रख सकते हैं। ए = "एएएएबी" में खोज एक्स = "एएएबी" के उदाहरण के साथ प्रदर्शित करना इतना आसान क्यों नहीं है। पहली परिकल्पना हमें चौथे चरित्र A : "AAAAB" की ओर ले जाती है, जहाँ हम एक बेमेल खोज करते हैं। यदि हम वापस नहीं आते हैं, तो हम प्रविष्टि नहीं पाते हैं, हालांकि यह मौजूद है।
गलत परिकल्पनाएं अपरिहार्य हैं, और परिस्थितियों के खराब सेट के तहत इस तरह के रोलबैक के कारण, यह पता चल सकता है कि हमने ए के बारे में प्रत्येक चरित्र की जाँच की है। एक्स | समय। यही है, कम्प्यूटेशनल जटिलता एल्गोरिथ्म ओ (| एक्स || ए ) की जटिलता है। तो एक पैराग्राफ में एक वाक्यांश के लिए खोज बाहर खींच सकते हैं ...
निष्पक्षता में, यह ध्यान दिया जाना चाहिए कि यदि लाइनें छोटी हैं, तो प्रोसेसर के दृष्टिकोण से अधिक पूर्वानुमान व्यवहार के कारण इस तरह के एल्गोरिथ्म "सही" एल्गोरिदम की तुलना में तेजी से काम कर सकता है।

जेड समारोह

एक स्ट्रिंग की खोज करने के सही तरीकों की श्रेणियों में से एक की गणना करना है, एक अर्थ में, दो तारों का सहसंबंध। सबसे पहले, हम ध्यान दें कि दो लाइनों की शुरुआत की तुलना करने का कार्य सरल और सीधा है: हम संबंधित अक्षरों की तुलना तब तक करते हैं जब तक हम एक विसंगति या किसी भी रेखा को समाप्त नहीं पाते। स्ट्रिंग के सभी प्रत्ययों के सेट पर विचार करें A : A [ | ए | .. ] ए [ | ए | -1 .. ] , ... ए [ 1 .. ] । हम इसके प्रत्येक प्रत्यय के साथ पंक्ति की शुरुआत की तुलना करेंगे। तुलना प्रत्यय के अंत तक पहुंच सकती है, या बेमेल के कारण किसी प्रतीक पर टूट सकती है। संयोग वाले भाग की लंबाई को किसी दिए गए प्रत्यय के लिए जेड-फ़ंक्शन का घटक कहा जाएगा।
यही है, जेड-फ़ंक्शन अपने प्रत्यय के साथ एक स्ट्रिंग के सबसे बड़े सामान्य उपसर्ग की लंबाई वेक्टर है। वाह! जब आप किसी को भ्रमित या मुखर करना चाहते हैं तो यह एक महान वाक्यांश है, लेकिन यह समझने के लिए कि यह क्या है, उदाहरण पर विचार करना बेहतर है।
मूल स्ट्रिंग "अबाकाबा" है । प्रत्येक प्रत्यय की स्ट्रिंग के साथ तुलना करते हुए, हमें जेड-फंक्शन के लिए एक प्लेट मिलती है:

प्रत्यय	पंक्ति		जेड
ababcaba	ababcaba	->	8
babcaba	ababcaba	->	0
abcaba	ababcaba	->	2
bcaba	ababcaba	->	0
काबा	ababcaba	->	0
ए.बी.ए.	ababcaba	->	3
बा	ababcaba	->	0
एक	ababcaba	->	1

प्रत्यय उपसर्ग एक विकल्प से अधिक कुछ नहीं है, और जेड-फ़ंक्शन उन सबस्ट्रिंग की लंबाई है जो शुरुआत और मध्य में एक साथ होते हैं। जेड-फ़ंक्शन के घटकों के सभी मूल्यों को ध्यान में रखते हुए, कोई कुछ नियमितताओं को नोटिस कर सकता है। सबसे पहले, यह स्पष्ट है कि जेड-फ़ंक्शन का मान स्ट्रिंग की लंबाई से अधिक नहीं है और केवल "पूर्ण" प्रत्यय ए [ 1 .. ] के लिए इसके साथ मेल खाता है (और इसलिए यह मान हमें रुचि नहीं देता है - हम इसे हमारे तर्क में छोड़ देंगे)। दूसरे, यदि एक एकल प्रतिलिपि में स्ट्रिंग में कोई एकल वर्ण है, तो यह केवल स्वयं के साथ मेल खा सकता है, और इसलिए यह स्ट्रिंग को दो भागों में विभाजित करता है, और जेड फ़ंक्शन का मूल्य कहीं भी छोटे हिस्से की लंबाई से अधिक नहीं हो सकता है।
इन टिप्पणियों का उपयोग निम्नानुसार प्रस्तावित है। मान लीजिए कि हम "अबका" की खोज करना चाहते हैं। हम इन पंक्तियों को ले लेते हैं और उनके बीच एक प्रहरी डालकर संक्षिप्त करते हैं: "अबका $ अबाबाकुबाकाब" । Z- फ़ंक्शन का वेक्टर इस तरह की रेखा के लिए दिखता है:

a b c $ a a b a b c a c a c a b

17 0 0 1 0 2 0 4 0 0 4 0 0 1 0 2 0

यदि हम पूर्ण प्रत्यय के लिए मान को त्याग देते हैं, तो संतरी की उपस्थिति Z _{i को} वांछित टुकड़े _की लंबाई तक सीमित कर देती है (यह समस्या के अर्थ में आधी रेखा से कम है)। लेकिन अगर यह अधिकतम तक पहुंच जाता है, तो केवल घटस्थापना की स्थिति में। हमारे उदाहरण में, चार वांछित लाइन की घटना के सभी पदों को चिह्नित करते हैं (ध्यान दें कि पाया गया अनुभाग एक-दूसरे के साथ ओवरलैप किया गया है, लेकिन हमारे सभी तर्क सही हैं)।
ठीक है, इसका मतलब है कि अगर हम जल्दी से एक जेड-फ़ंक्शन के वेक्टर का निर्माण कर सकते हैं, तो स्ट्रिंग के सभी घटनाओं की खोज करने के लिए इसका उपयोग करते हुए, इसमें इसकी लंबाई को कम करना कम कर देता है। लेकिन केवल अगर हम प्रत्येक प्रत्यय के लिए जेड-फ़ंक्शन की गणना करते हैं, तो यह स्पष्ट रूप से "हेड-ऑन" समाधान से तेज नहीं होगा। यह हमें मदद करता है कि वेक्टर के अगले तत्व का मूल्य पिछले तत्वों के आधार पर पता लगाया जा सकता है।
मान लीजिए कि हमने किसी तरह Z-फ़ंक्शन के मूल्यों की गणना इसी i-1st वर्ण तक की है। एक निश्चित स्थिति पर विचार करें r <i, जहां हम पहले से ही Z _{r को} जानते हैं।
तो इस स्थिति से Z _r अक्षर ठीक उसी तरह हैं जैसे लाइन की शुरुआत में। वे तथाकथित जेड-ब्लॉक बनाते हैं। हम सबसे सही जेड-ब्लॉक में दिलचस्पी लेंगे, अर्थात, जो सबसे दूर का अंत करता है (बहुत पहले गिनती नहीं करता है)। कुछ मामलों में, सबसे सही ब्लॉक शून्य लंबाई का हो सकता है (जब कोई भी गैर-रिक्त ब्लॉक i-1 को शामिल नहीं करता है, तो i-1st सबसे सही होगा, भले ही Z _i-1 = 0)।

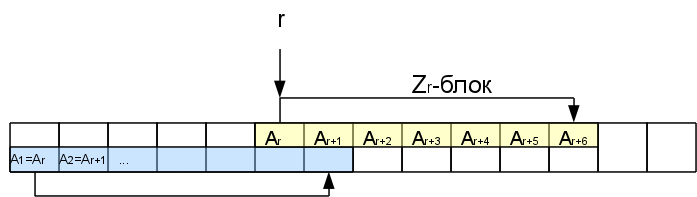
जब हम इस जेड-ब्लॉक के बाद के वर्णों पर विचार करते हैं, तो अगले प्रत्यय की शुरुआत से तुलना करने का कोई मतलब नहीं है, क्योंकि इस प्रत्यय का एक हिस्सा पहले से ही लाइन की शुरुआत में आ चुका है, जिसका अर्थ है कि यह पहले से ही संसाधित हो चुका है। आप तुरंत वर्णों को जेड-ब्लॉक के अंत तक छोड़ सकते हैं।


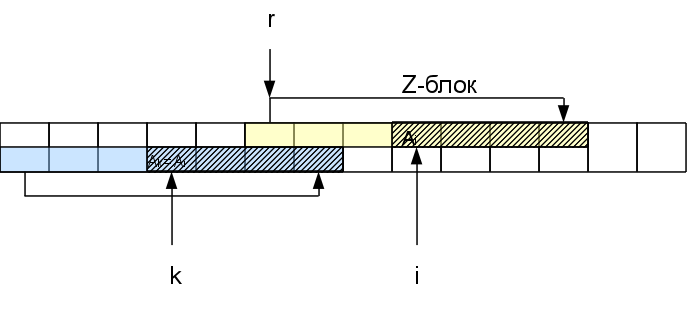
अर्थात्, यदि हम Z _r -block में स्थित i-th वर्ण पर विचार करते हैं, अर्थात् स्थिति k = i-r + 1 पर पंक्ति के आरंभ में संबंधित वर्ण। फ़ंक्शन Z _k हमें पहले से ही ज्ञात है। यदि यह Z _r - (ir) की दूरी Z- ब्लॉक के अंत तक शेष है, तो हम तुरंत यह सुनिश्चित कर सकते हैं कि इस चिन्ह के लिए पूरा संयोग क्षेत्र r -th Z-block के अंदर है और इसका अर्थ है कि परिणाम समान होगा लाइन की शुरुआत: Z _i = Z _k यदि Z _k > = Z _r - (ir), तो Z _i , Z _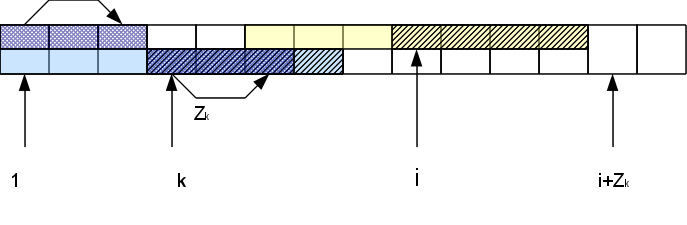r - (ir) से अधिक या बराबर है। यह पता लगाने के लिए कि यह कितना अधिक है, हमें जेड-ब्लॉक के बाद वर्णों की जांच करने की आवश्यकता होगी। इसके अलावा, यदि इन वर्णों में से रेखा के आरंभ में संगत लोगों के साथ मेल खाता है, तो Z _i , h: Z _i = Z _k + h से बढ़ता है। परिणामस्वरूप, हमारे पास एक नया सबसे दाहिना Z-block (यदि h> 0) हो सकता है।

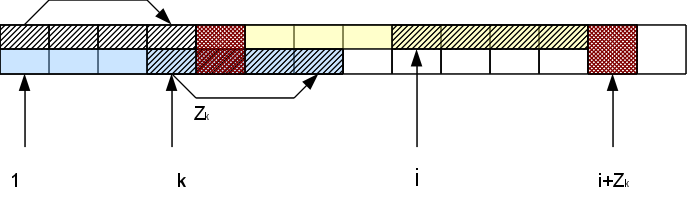
इस प्रकार, हमें केवल प्रतीकों की तुलना सबसे सही Z- ब्लॉक के दाईं ओर करनी है, और सफल तुलना के कारण, ब्लॉक "दाईं ओर" चलता है, और असफल लोग रिपोर्ट करते हैं कि इस स्थिति के लिए गणना समाप्त हो गई है। यह हमें स्ट्रिंग की लंबाई के साथ रैखिक समय में जेड-फ़ंक्शन के पूरे वेक्टर के निर्माण के साथ प्रदान करता है।
प्रतिस्थापन के लिए खोज करने के लिए इस एल्गोरिथ्म को लागू करते हुए, हम समय जटिलता ओ (( ए | ए | + | एक्स |)) प्राप्त करते हैं, जो पहले संस्करण में मौजूद उत्पाद से बहुत बेहतर है। सच है, हमें जेड-फ़ंक्शन के लिए एक वेक्टर स्टोर करना था, जो ऑर्डर ओ की अतिरिक्त मेमोरी लेगा (| ए | ए | एक्स ।)। वास्तव में, यदि आपको सभी घटनाओं को खोजने की आवश्यकता नहीं है, लेकिन केवल एक ही पर्याप्त है, तो O (! X |) मेमोरी के साथ भेजा जा सकता है, क्योंकि Z- ब्लॉक की लंबाई से अधिक नहीं हो सकती है। एक्स | इसके अलावा, आप पहली घटना का पता लगाने के बाद लाइन को जारी नहीं रख सकते।
अंत में, एक फ़ंक्शन का एक उदाहरण जो जेड-फ़ंक्शन की गणना करता है। बिना किसी ट्रिक के बस एक मॉडल संस्करण।

 void z_preprocess(vector<int> & Z, const string & str) { const size_t len = str.size(); Z.clear(); Z.resize(len); if (0 == len) return; Z[0] = len; for (size_t curr = 1, left = 0, right = 1; curr < len; ++curr) { if (curr >= right) { size_t off = 0; while ( curr + off < len && str[curr + off] == str[off] ) ++off; Z[curr] = off; right = curr + Z[curr]; left = curr; } else { const size_t equiv = curr - left; if (Z[equiv] < right - curr) Z[curr] = Z[equiv]; else { size_t off = 0; while ( right + off < len && str[right - curr + off] == str[right + off] ) ++off; Z[curr] = right - curr + off; right += off; left = curr; } } } } 
 

void z_preprocess(vector<int> & Z, const string & str) { const size_t len = str.size(); Z.clear(); Z.resize(len); if (0 == len) return; Z[0] = len; for (size_t curr = 1, left = 0, right = 1; curr < len; ++curr) { if (curr >= right) { size_t off = 0; while ( curr + off < len && str[curr + off] == str[off] ) ++off; Z[curr] = off; right = curr + Z[curr]; left = curr; } else { const size_t equiv = curr - left; if (Z[equiv] < right - curr) Z[curr] = Z[equiv]; else { size_t off = 0; while ( right + off < len && str[right - curr + off] == str[right + off] ) ++off; Z[curr] = right - curr + off; right += off; left = curr; } } } }


नूथ-मॉरिस-प्रैट एलगोरिदम (केएमपी)

पिछली पद्धति की तार्किक सादगी के बावजूद, एक और एल्गोरिथ्म अधिक लोकप्रिय है, जो एक अर्थ में जेड-फ़ंक्शन का उलटा है - नॉट-मॉरिस-प्रैट (केएमपी) एल्गोरिदम । हम एक उपसर्ग फ़ंक्शन की अवधारणा को पेश करते हैं। I-th स्थिति के लिए उपसर्ग फ़ंक्शन अधिकतम पंक्ति उपसर्ग की लंबाई है जो कि i से छोटी है और जो लंबाई i के उपसर्ग के प्रत्यय से मेल खाती है। यदि जेड-फ़ंक्शन की परिभाषा प्रतिद्वंद्वी को पूरी तरह से नहीं हराती है, तो इस कॉम्बो के साथ आप निश्चित रूप से इसे अपनी जगह पर रखने में सक्षम होंगे :) और मानव भाषा में यह इस तरह दिखता है: हम हर संभव रेखा उपसर्ग लेते हैं और उपसर्ग के अंत के साथ सबसे लंबी शुरुआत के संयोग को देखते हैं (खाते में तुच्छ संयोग नहीं लेते। अपने आप से)। यहाँ "अब्बाबाबा" के लिए एक उदाहरण दिया गया है:

उपसर्ग	उपसर्ग	पी
एक	एक	0
अब	अब	0
अब ए	a बा	1
एब एब	एब एब	2
ababc	ababc	0
ababc a	एक बाबा	1
ababc ab	ab अबकाब	2
ababc अबा	अबा बकाबा	3

फिर से, हम उपसर्ग फ़ंक्शन के कई गुणों का निरीक्षण करते हैं। सबसे पहले, मूल्यों को उनकी संख्या से ऊपर बांधा जाता है, जो सीधे परिभाषा से अनुसरण करता है - उपसर्ग की लंबाई उपसर्ग फ़ंक्शन से अधिक होनी चाहिए। दूसरे, एक अद्वितीय चरित्र उसी तरह एक स्ट्रिंग को दो भागों में विभाजित करता है और एक उपसर्ग फ़ंक्शन के अधिकतम मूल्य को भागों के छोटे हिस्से की लंबाई तक सीमित करता है - क्योंकि अब जो कुछ भी होता है उसमें एक अद्वितीय चरित्र होता है जो किसी और चीज़ के बराबर नहीं होता है।
इससे हमें वह निष्कर्ष मिलता है जिसमें हम रुचि रखते हैं। मान लीजिए कि हमने इस सैद्धांतिक छत के कुछ तत्व को हासिल किया। इसका मतलब यह है कि इस तरह के एक उपसर्ग यहाँ समाप्त हो गया है कि प्रारंभिक भाग अंतिम एक के साथ मेल खाता है और उनमें से एक "पूर्ण" आधा का प्रतिनिधित्व करता है। यह स्पष्ट है कि उपसर्ग में पूर्ण आधा सामने होना चाहिए, जिसका अर्थ है कि इस धारणा के साथ यह आधा छोटा होना चाहिए, लेकिन हम अधिकतम आधे पर अधिकतम तक पहुंचते हैं।
इस प्रकार, यदि हम पिछले भाग की तरह, वांछित रेखा को उस स्थिति से समेटते हैं, जिसमें हम प्रहरी के माध्यम से देख रहे हैं, तो उपसर्ग फ़ंक्शन के घटक में वांछित प्रतिस्थापन की लंबाई के प्रवेश का बिंदु उस स्थान के अनुरूप होगा जहां प्रवेश समाप्त होता है। हमारा उदाहरण लें: लाइन में "ababcabcacab" हम "abca" की तलाश में हैं । "अबका $ अबबाकैकाब" का एक संक्षिप्त संस्करण। उपसर्ग फ़ंक्शन इस तरह दिखता है:

a b c $ a a b a b c a c a c a b

0 0 0 1 0 1 2 2 1 2 3 4 2 3 4 4 1 1 2

फिर से, हमने पाया कि सबस्टेशन की सभी घटनाएँ एक झटके में खत्म हो गईं - वे चार में खत्म हो गईं। यह समझने के लिए बना हुआ है कि इस उपसर्ग फ़ंक्शन को कुशलता से कैसे गणना किया जाए। एल्गोरिथ्म का विचार जेड-फ़ंक्शन के निर्माण के विचार से थोड़ा अलग है।

उपसर्ग फ़ंक्शन का बहुत पहला मूल्य स्पष्ट रूप से है 0. आइए हम उपसर्ग फ़ंक्शन को ith स्थिति तक और इसमें शामिल करते हैं। I + 1 वर्ण पर विचार करें। यदि i-th स्थिति में उपसर्ग फ़ंक्शन का मान Pi है, तो उपसर्ग A [ .. Pi ] विकल्प A [ iP _i + 1..i ] के साथ मेल खाता है। यदि प्रतीक A [ P _i + +1 ] A [ i + 1 ] से मेल खाता है, तो हम सुरक्षित रूप से P _{i + 1} = P _i +1 लिख सकते हैं। लेकिन यदि नहीं, तो मान या तो कम या समान हो सकता है। बेशक, Pi = 0 के साथ, कहीं ज्यादा कमी नहीं है, इसलिए इस मामले में Pi _{+ 1} = 0 है। मान लें कि पी _i > 0। तब स्ट्रिंग में एक उपसर्ग A [ ..P _i ] होता है, जो कि A [ iP _i + 1..i ] के विकल्प के बराबर होता है। वांछित उपसर्ग फ़ंक्शन इन समतुल्य वर्गों के भीतर बनता है और संसाधित होने वाला वर्ण, जिसका अर्थ है कि हम उपसर्ग के बाद पूरी पंक्ति के बारे में भूल सकते हैं और केवल इस उपसर्ग और i + 1 वर्ण को छोड़ सकते हैं - स्थिति समान होगी।

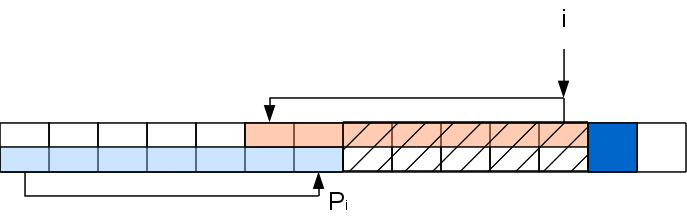
इस चरण के कार्य को कट आउट मिडिल वाली रेखा के लिए समस्या को कम किया गया था: A [ ..P _i ] A [ i + 1 ] , जिसे एक ही तरीके से पुनरावर्ती रूप से हल किया जा सकता है (हालाँकि पूंछ पुनरावृत्ति बिल्कुल नहीं है, लेकिन एक लूप)। यही है, यदि A [ P _{P i} +1 ] A [ i + 1 ] के साथ मेल खाता है, तो P _{i + 1} = P _{P i} +1, अन्यथा हम फिर से विचार से रेखा का भाग बाहर फेंक देते हैं, आदि। हम प्रक्रिया को तब तक दोहराते हैं जब तक हमें कोई मेल नहीं मिलता या 0 नहीं मिलता।

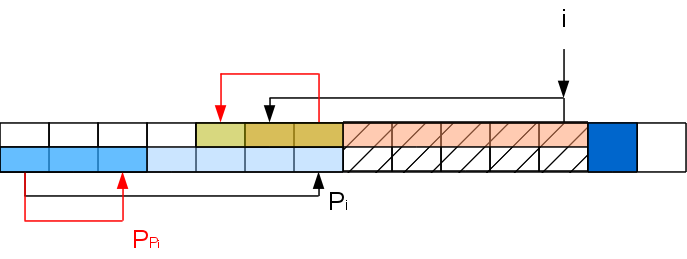
इन परिचालनों की पुनरावृत्ति सतर्क होनी चाहिए - ऐसा लगेगा कि हमें दो नेस्टेड चक्र मिलते हैं। लेकिन ऐसा है नहीं। तथ्य यह है कि कश्मीर पुनरावृत्तियों की लंबाई के साथ एक नेस्टेड लूप कम से कम k-1 द्वारा i + 1st स्थिति में उपसर्ग फ़ंक्शन को कम कर देता है, और इस तरह के मूल्य को उपसर्ग फ़ंक्शन को बढ़ाने के लिए, आपको कम से कम k-1 की आवश्यकता है k-1 वर्णों को संसाधित करके अक्षरों का मिलान करें। यही है, चक्र की लंबाई ऐसे चक्रों के निष्पादन के बीच अंतराल से मेल खाती है और इसलिए एल्गोरिथ्म की जटिलता अभी भी संसाधित स्ट्रिंग की लंबाई के साथ रैखिक है। यहां स्थिति जेड-फ़ंक्शन के साथ मेमोरी के समान है - लाइन की लंबाई के साथ रैखिक, लेकिन बचाने का एक तरीका है। इसके अलावा, एक सुविधाजनक तथ्य यह है कि पात्रों को क्रमिक रूप से संसाधित किया जाता है, अर्थात, यदि हम पहले से ही पहली घटना प्राप्त कर चुके हैं तो हमें पूरी लाइन को संसाधित करने की आवश्यकता नहीं है।
उदाहरण के लिए, कोड का एक टुकड़ा:

 void calc_prefix_function(vector<int> & prefix_func, const string & str) { const size_t str_length = str.size(); prefix_func.clear(); prefix_func.resize(str_length); if (0 == str_length) return; prefix_func[0] = 0; for (size_t current = 1; current < str_length; ++current) { size_t matched_prefix = current - 1; size_t candidate = prefix_func[matched_prefix]; while (candidate != 0 && str[current] != str[candidate]) { matched_prefix = prefix_func[matched_prefix] - 1; candidate = prefix_func[matched_prefix]; } if (candidate == 0) prefix_func[current] = str[current] == str[0] ? 1 : 0; else prefix_func[current] = candidate + 1; } } 
 

void calc_prefix_function(vector<int> & prefix_func, const string & str) { const size_t str_length = str.size(); prefix_func.clear(); prefix_func.resize(str_length); if (0 == str_length) return; prefix_func[0] = 0; for (size_t current = 1; current < str_length; ++current) { size_t matched_prefix = current - 1; size_t candidate = prefix_func[matched_prefix]; while (candidate != 0 && str[current] != str[candidate]) { matched_prefix = prefix_func[matched_prefix] - 1; candidate = prefix_func[matched_prefix]; } if (candidate == 0) prefix_func[current] = str[current] == str[0] ? 1 : 0; else prefix_func[current] = candidate + 1; } }

इस तथ्य के बावजूद कि एल्गोरिथ्म अधिक जटिल है, जेड-फ़ंक्शन की तुलना में इसका कार्यान्वयन और भी सरल है।

अन्य खोज कार्य

फिर बस बहुत सारे पत्र चले जाएंगे कि स्ट्रिंग्स खोज कार्य इस तक सीमित नहीं हैं और यह कि अन्य कार्य और अन्य समाधान हैं, इसलिए यदि आप रुचि नहीं रखते हैं, तो आप आगे नहीं पढ़ सकते हैं। यह जानकारी केवल परिचित करने के लिए है, ताकि, यदि आवश्यक हो, तो कम से कम इस बात से अवगत रहें कि "सब कुछ हमारे सामने चोरी हो गया है" और पहिया को फिर से स्थापित करने के लिए नहीं।
यद्यपि ऊपर वर्णित एल्गोरिदम, रैखिक निष्पादन समय की गारंटी देते हैं, बॉयर-मूर एल्गोरिथ्म ने "डिफ़ॉल्ट एल्गोरिथ्म " शीर्षक प्राप्त किया। औसतन, यह रैखिक समय भी देता है, लेकिन इस रैखिक कार्य के लिए एक बेहतर स्थिरांक भी है, लेकिन यह औसतन है। "खराब" डेटा हैं, जिस पर यह एक सरल तुलना "हेड-ऑन" से बेहतर नहीं है (ठीक है, जैसे कि क्यूसॉर्ट के साथ)। यह बेहद भ्रामक है और हम इस पर विचार नहीं करेंगे - वैसे भी, उल्लेख करने के लिए नहीं। कई विदेशी एल्गोरिदम हैं जो प्राकृतिक भाषा पाठ प्रसंस्करण पर ध्यान केंद्रित करते हैं और उनकी अनुकूलन में शब्दों के सांख्यिकीय गुणों पर भरोसा करते हैं।
ठीक है, हमारे पास एक एल्गोरिथ्म है जो किसी भी तरह से O (| X | + | + | A |) के लिए स्ट्रिंग में सबस्ट्रिंग की खोज करता है। अब कल्पना करें कि हम एक गेस्टबुक इंजन लिख रहे हैं। हमारे पास निषिद्ध अश्लील शब्दों की एक सूची है (यह स्पष्ट है कि यह मदद नहीं करेगा, लेकिन कार्य केवल उदाहरण के लिए है)। हम संदेशों को फ़िल्टर करने जा रहे हैं। हम संदेश में निषिद्ध शब्दों में से प्रत्येक की खोज करेंगे और ... यह हमें ले जाएगा O (| X ₁ | + | X ₂ | + ... + + X _n | + n | A |) | किसी भी तरह से, खासकर अगर "महान और शक्तिशाली" के "शक्तिशाली अभिव्यक्ति" का शब्दकोश बहुत "शक्तिशाली" है। इस मामले के लिए, खोज स्ट्रिंग्स के शब्दकोश को प्रीप्रोसेस करने का एक तरीका है ताकि खोज केवल O! X X ₁ + + | X ₂ | + ... + | X _n | + | A |) पर काबिज हो जाए, और यह विशेष रूप से काफी कम हो सकता है। यदि संदेश लंबे हैं।
इस तरह के पूर्व-प्रसंस्करण शब्दकोश से एक त्रि का निर्माण करने के लिए नीचे आता है: पेड़ कुछ डमी रूट में शुरू होता है, नोड्स शब्दकोष में शब्दों के अक्षरों के अनुरूप होते हैं, पेड़ के नोड की गहराई शब्द में पत्र की संख्या से मेल खाती है। जिन नोड्स पर शब्द कोश से समाप्त होता है, उन्हें टर्मिनल कहा जाता है और किसी तरह से चिह्नित किया जाता है (चित्र में लाल)।

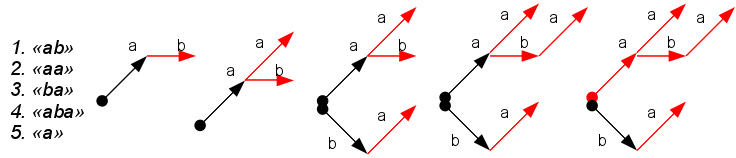
परिणामस्वरूप पेड़ KMP एल्गोरिथ्म के उपसर्ग समारोह का एक एनालॉग है। इसके साथ, आप शब्दकोश वाक्यांश में सभी शब्दों की सभी घटनाओं को पा सकते हैं। हमें पेड़ के माध्यम से जाना चाहिए, एक पेड़ के नोड के रूप में अगले चरित्र की उपस्थिति की जांच करना, साथ ही साथ सामना किए गए टर्मिनल कोने को चिह्नित करना - ये शब्दों की घटनाएं हैं। यदि पेड़ में कोई समान नोड नहीं है, तो, जैसा कि आईएलसी में, विशेष लिंक का उपयोग करके पेड़ में रोलबैक अधिक होता है। इस एल्गोरिथ्म को अहो-कोरसिक एल्गोरिथ्म कहा जाता है । उसी योजना का उपयोग इनपुट के दौरान खोज करने और इलेक्ट्रॉनिक शब्दकोशों में अगले चरित्र की भविष्यवाणी करने के लिए किया जा सकता है।
इस उदाहरण में, बोरॉन का निर्माण सरल है: हम बदले में बोरॉन में शब्द जोड़ते हैं (केवल "किकबैक" के लिए अतिरिक्त लिंक के साथ बारीकियों)। इस पेड़ की स्मृति उपयोग को कम करने के उद्देश्य से कई अनुकूलन हैं (तथाकथित बोरान संपीड़न - शाखाओं के बिना अनुभागों को छोड़ देना)। व्यवहार में, ये अनुकूलन लगभग अनिवार्य हैं। इस एल्गोरिथ्म का नुकसान इसकी वर्णानुक्रमिक निर्भरता है: नोड के प्रसंस्करण का समय और कब्जे वाली स्मृति संभावित बच्चों की संख्या पर निर्भर करती है, जो वर्णमाला के आकार के बराबर है। बड़े अक्षर के लिए, यह एक गंभीर समस्या है (यूनिकोड वर्णों के एक सेट की कल्पना करें?)। आप इस सब के बारे में इस हैब्रोटोपिका में या Google इंडेक्स का उपयोग करके अधिक पढ़ सकते हैं - इस मुद्दे पर बहुत सारी जानकारी है।
अब हम दूसरे कार्य को देखते हैं। यदि पिछले एक में हम पहले से जानते थे कि बाद में आने वाले डेटा में हमें क्या खोजने की आवश्यकता है, तो यहां यह बिल्कुल विपरीत है: हमें अग्रिम में एक पंक्ति दी गई थी जिसमें वे खोज करेंगे, लेकिन वे जो खोजेंगे वह अज्ञात है, लेकिन वे बहुत खोज करेंगे। एक विशिष्ट उदाहरण एक खोज इंजन है। जिस दस्तावेज़ में शब्द खोजा गया है, वह पहले से जाना जाता है, लेकिन वहाँ खोजे जाने वाले शब्द चलते-फिरते हैं। प्रश्न है, फिर से, O के बदले कैसे (? X ₁ | + | X ₂ | + ... + | + X _n = _n | n | A ) O पाने के लिए (| X ₁ | + | X ₂ | + ... + | | एक्स _एन | + | ए |) |
यह एक बोरान बनाने का प्रस्ताव है जिसमें मौजूदा स्ट्रिंग के सभी संभावित प्रत्यय होंगे। तब टेम्पलेट के लिए खोज वांछित टेम्पलेट के अनुरूप पेड़ में पथ की उपस्थिति की जांच करने के लिए कम हो जाएगी। यदि आप सभी प्रत्ययों की संपूर्ण खोज के द्वारा इस तरह के बोरॉन का निर्माण करते हैं, तो यह प्रक्रिया O (| - ² ) समय और बहुत सारी मेमोरी ले सकती है। लेकिन, सौभाग्य से, ऐसे एल्गोरिदम हैं जो आपको एक संपीड़ित रूप में इस तरह के पेड़ को तुरंत बनाने की अनुमति देते हैं - एक प्रत्यय पेड़ , और इसे ओ (! ए |) में करते हैं। हाल ही में Habré पर इस बारे में एक लेख आया था, इसलिए जो लोग रुचि रखते हैं, वे उककोन एल्गोरिथम के बारे में पढ़ सकते हैं।
एक प्रत्यय के पेड़ में दो चीजें खराब होती हैं, हमेशा की तरह: यह एक पेड़ है, और यह कि पेड़ के नोड्स वर्णानुक्रम पर निर्भर हैं। प्रत्यय सरणी इन कमियों को बख्शा गया है । प्रत्यय सरणी का सार यह है कि यदि स्ट्रिंग के सभी प्रत्ययों को क्रमबद्ध किया जाता है, तो वांछित पैटर्न के पहले अक्षर द्वारा आसन्न प्रत्ययों के समूह की खोज के लिए सबस्ट्रिंग की खोज कम हो जाएगी और बाद के लोगों के लिए सीमा को और परिष्कृत किया जाएगा। इसी समय, प्रत्ययों को स्वयं को क्रमबद्ध रूप में संग्रहीत करने की आवश्यकता नहीं है, यह उन पदों को संग्रहीत करने के लिए पर्याप्त है जिन पर वे स्रोत डेटा में शुरू करते हैं। सही है, इस संरचना की समय निर्भरता थोड़ी खराब है: एक खोज में O (! X | + log | - |) खर्च होगा यदि आप इस बारे में सोचते हैं और सब कुछ ध्यान से करते हैं, और यदि आप परेशान नहीं हैं, तो O ((! X | log | A |)। तुलना के लिए, पेड़ में निश्चित वर्णमाला O (| X |) के लिए। लेकिन तथ्य यह है कि यह एक सरणी है, न कि एक पेड़, मेमोरी कैशिंग के साथ स्थिति में सुधार कर सकता है और प्रोसेसर संक्रमण भविष्यवक्ता के कार्य को सुविधाजनक बना सकता है। Kärkkäinen-Sanders एल्गोरिथ्म का उपयोग करके रैखिक समय में एक प्रत्यय सरणी का निर्माण किया गया है (मुझे क्षमा करें, लेकिन मुझे पता नहीं है कि यह रूसी में ध्वनि कैसे होनी चाहिए)। आज यह सबसे लोकप्रिय पंक्ति अनुक्रमण विधियों में से एक है।
यहां हम लगभग स्ट्रिंग खोज और समानता की डिग्री के विश्लेषण के प्रश्नों पर नहीं छूएंगे - यह इस लेख में रटना करने के लिए बहुत बड़ा क्षेत्र है। मैं सिर्फ इस बात का उल्लेख करूंगा कि लोगों ने कुछ नहीं के लिए रोटी नहीं खाई और बहुत सारे दृष्टिकोणों के साथ आए, इसलिए यदि आप एक समान समस्या का सामना करते हैं, तो खोजें और पढ़ें। संभवतः, यह समस्या पहले ही हल हो चुकी है।

पढ़ने वालों को धन्यवाद! और जिन लोगों ने इसे पढ़ा है, उन्हें बहुत-बहुत धन्यवाद!

UPD: बोरान के बारे में एक पर्याप्त लेख के लिए एक लिंक जोड़ा गया है (यह एक किरण है, यह एक उपसर्ग वृक्ष है, यह एक भरा हुआ पेड़ है, यह त्रि है)।