🈶 🎧 👩🏻‍🔬 फूरियर रूपांतरण का उपयोग कर बहुपद का बहुगुणना आसान है 🎄 🛰️ 👾

शुभ संध्या
यह पोस्ट तेजी से फूरियर रूपांतरण के बारे में है। प्रत्यक्ष और उलटा रूपांतर (जटिल संख्या में) माना जाएगा। अगले भाग में, मैं ओलम्पियाड प्रोग्रामिंग की कुछ समस्याओं (विशेष रूप से, तार की "समानता" के बारे में एक समस्या) में उनके अनुप्रयोगों पर विचार करने की योजना बना रहा हूं, और पूर्णांकों में रूपांतरण के कार्यान्वयन के बारे में भी बात करता हूं।
FFT एक एल्गोरिथ्म है जो समय n में कुछ n बिंदुओं पर डिग्री n = 2 ^{k के} बहुपद के मानों की गणना करता है ( n (log n ) ("भोले" विधि समय O ( n ² ) में एक ही कार्य करता है)। उसी समय, आप उलटा परिवर्तन कर सकते हैं। संख्याओं के जोड़, घटाव और गुणा को जोड़ने के बाद से, बहुपद (विशेष रूप से गुणा) की तुलना में बहुत आसान है, FFT का उपयोग अक्सर बहुपद और लंबी संख्या के साथ गणना को गति देने के लिए किया जाता है।

परिभाषाएँ और उपयोग

सबसे पहले, आइए परिभाषित करें कि एक बहुपद क्या है:
P ( x ) = a ₀ + x a ₁ + x ² a ₂ + x ³ a ₃ + ... + x ^{n - 1} a _{n - 1}

जटिल संख्या

यदि आप जटिल संख्याओं से परिचित हैं, तो आप इस बिंदु को छोड़ सकते हैं, अन्यथा, यहाँ एक संक्षिप्त परिभाषा है:
x = a + i b , जहाँ मैं ² = - 1
यहाँ a को वास्तविक ( Real ) भाग कहा जाता है, और b काल्पनिक ( Imaginary ) भाग है। जैसा कि आप देख सकते हैं, कोई भी इन नंबरों से नकारात्मक (और वास्तव में किसी भी) संख्याओं से एक जड़ निकाल सकता है - यह बहुपद के साथ काम करते समय बहुत सुविधाजनक है - बीजगणित के मुख्य प्रमेय से निम्नानुसार, डिग्री एन के प्रत्येक बहुपद में बिल्कुल जटिल जड़ें होती हैं (खाते को गुणा करना )।
विमान पर बिंदुओं के रूप में उनका प्रतिनिधित्व करना भी बहुत सुविधाजनक है:

जटिल संख्याओं की एक और उल्लेखनीय संपत्ति यह है कि उन्हें x = (cosα + i sinα) r के रूप में दर्शाया जा सकता है, जहां α "संख्या" (एक तर्क कहा जाता है ) का ध्रुवीय कोण है, और r शून्य से इसकी दूरी ( मापांक ) है। और दो संख्याओं को गुणा करने पर:
a = (cosα + i cos sinα) r _a
b = (cos r + i βsin () r _b
a b = (cosα + i insinα) (cos i + i βsinβ) r r _b
a b = (cosα⋅cosβ-sinαβsin i + i (sinαβcosβ + cosβ⋅sinα)) r r _b
a b = (cos (α + β) + i sin (α + ()) r r _b
उनके मॉड्यूल गुणा किए जाते हैं, और तर्क जोड़ दिए जाते हैं।

1 की जटिल जड़ें

अब आइए समझते हैं कि 1 से nth डिग्री की जटिल जड़ें कैसी दिखती हैं। X ⁿ = 1 को दें , तो इसका मॉड्यूल स्पष्ट रूप से एकता के बराबर है, और n xarg x = 2 is k , जहां k एक पूर्णांक है। इसका मतलब यह है कि संख्या को अपने आप से गुणा करने के बाद (जो कि nth पावर तक बढ़ रही है), इसका तर्क "कई" 2 multiple (360 डिग्री) हो जाएगा।
संख्या के सूत्र को याद करें, यदि तर्क और मॉड्यूल ज्ञात हैं, तो हम प्राप्त करते हैं:
α = 2 / x / n , जहां 0 x
ω _i = cosα + i insinα
यानी यदि आप ड्रा करते हैं, तो हमें बराबर अंतराल पर सर्कल पर केवल अंक मिलते हैं:

कृपया तीन चीजों पर ध्यान दें जिनका हम सक्रिय रूप से उपयोग करेंगे (उनके बिना, कुछ भी काम नहीं करेगा):
= a ω _b = ω _{( a + b ) mod n}
ω ₀ + ω ₁ + + ₂ + ... + _{1 n - 1} = 0
ω ₀ ^{n / 2} = ⁿ ₂ ^{n / 2} = ² ₄ ^{n / 2} = ... = 1 ( n के लिए भी)
इन गुणों के कारण, यह इन बिंदुओं पर है कि हम बहुपद के मूल्य पर विचार करेंगे। बेशक, परिणाम जरूरी वास्तविक नहीं होंगे, इसलिए कार्यक्रम को जटिल संख्याओं के साथ काम करने की आवश्यकता होगी।

जड़ों का योग शून्य क्यों है

प्रमाण बहुत सरल है: φ = is ₀ + + ₁ + ... दें। दोनों पक्षों को ( ₁ (! = 1) से गुणा करें। क्योंकि ω _i ω ₁ = ω _{i + 1} , फिर ω ₁ = ω ₁ + ω ₂ + ... + + _{n - 1} + ω ₀ । शब्दों के पुनर्व्यवस्था से, योग नहीं बदलता है, इसलिए, क्रमशः φ⋅ω = range ₁ , ω (= ₁ - 1 ) = 0 । क्योंकि ω ₁ ! = 1, फिर φ = 0 ।

यह कैसे काम करता है

हम मानते हैं कि हमारे बहुपद में डिग्री n = 2 ^{k है} । यदि नहीं, तो हम दो के निकटतम शक्ति के लिए अग्रणी गुणांक को शून्य के साथ पूरक करते हैं।
एफएफटी का मूल विचार बहुत सरल है:
करते हैं:
A ( x ) = a ₀ + x a ₂ + x ² a ₄ + ... + x ^{n / 2 - 1} a _{n - 2} (गुणांक P )
B ( x ) = ₁ + x a ₃ + x ² a ₅ + ... + x ^{n / 2 - 1} a _{n - 1} (विषम गुणांक P )।
फिर P ( x ) = A ( x ² ) + x x B ( x ² )।
अब हम "विभाजित और जीतते हैं" के सिद्धांत को लागू करते हैं: n बिंदुओं पर P के मानों की गणना करने के लिए (, ₀ , of ₁ , ... ), हम A और B के मानों की गणना n / 2 बिंदुओं पर करते हैं (, ₀ , ω ₂ , ... ) । अब P का मूल्य (ω _i ) पुनर्प्राप्त करने के लिए काफी सरल है:
P ( _{i i} ) = A (ω _{2 i} ) + ⋅ _i ω B ( _{i 2 i} )
यदि हम ξ _i = den _{2 से} निरूपित _करते हैं, तो जिन बिंदुओं पर हम डिग्री n / 2 के बहुपद के मानों पर विचार करते हैं, वह सूत्र रूपांतरित हो जाएगा:
P () _i ) = A (ξ _i ) +) _i ξ B (ω _i )
यह पहले से ही प्रोग्राम में संचालित किया जा सकता है, यह भूलकर कि मैं 0 से n - 1 तक मान लेता हूं , और ξ _{i को} केवल 0 से n / 2 - 1 तक परिभाषित किया गया है। निष्कर्ष - i modulo n / 2 लेना आवश्यक होगा।
ऑपरेटिंग समय पुनरावृत्ति सूत्र T ( n ) = O ( n ) + 2 T ( n / 2 ) द्वारा व्यक्त किया जाता है। यह एक काफी प्रसिद्ध संबंध है और यह O ( n nlog ₂ n ) में प्रकट होता है (लगभग बोलते हुए, पुनरावृत्ति की गहराई ₂ स्तर n लॉग होती है, प्रत्येक स्तर पर O ( n ) ऑपरेशन सभी कॉल के लिए कुल में किए जाते हैं)।

कुछ लिखो

यहाँ एक अक्षम पुनरावर्ती एफएफटी कार्यान्वयन का एक उदाहरण है:

धीमे धीमे

#include <vector> #include <complex> using namespace std; typedef complex<double> cd; // STL-  .   double,     sin  cos typedef vector<cd> vcd; vcd fft(const vcd &as) { //       1 int n = as.size(); // -    ? if (n == 1) return vcd(1, as[0]); vcd w(n); //   for (int i = 0; i < n; i++) { double alpha = 2 * M_PI * i / n; w[i] = cd(cos(alpha), sin(alpha)); } //   A  B vcd A(n / 2), B(n / 2); for (int i = 0; i < n / 2; i++) { A[i] = as[i * 2]; B[i] = as[i * 2 + 1]; } vcd Av = fft(A); vcd Bv = fft(B); vcd res(n); for (int i = 0; i < n; i++) res[i] = Av[i % (n / 2)] + w[i] * Bv[i % (n / 2)]; return res; }

आप I / O जोड़ सकते हैं और अपने कार्यान्वयन की शुद्धता को सत्यापित कर सकते हैं। बहुपद पी ( x ) = 4 + 3 x + 2 x ² + x ³ + 0 ⁴ x ⁴ + 0 + x ⁵ + 0 ⁶ x ⁶ + 0 x ⁷ मान इस प्रकार हैं:
पी ( डब्ल्यू ₀ ) = ( 1 0. 0 0 0 , 0. 0 0 0 )
पी ( डब्ल्यू ₁ ) = ( 5. 4 1 4 , 4. 8 2 8 )
P ( w ₂ ) = ( 2. 0 0 0 , 2. 0 0 0 )
पी ( डब्ल्यू ₃ ) = ( 2. 5 8 6 , 0. 8 2 8 )
P ( w ₄ ) = ( 2. 0 0 0 , 0. 0 0 0 )
P ( w ₅ ) = ( 2. 5 8 6 , - 0. 8 2 8 )
पी ( डब्ल्यू ₆ ) = ( 2. 0 0 0 , - 2. 0 0 0 )
पी ( डब्ल्यू ₇ ) = ( 5. 4 1 4 , - 4. 8 2 8 )
यदि हां, तो आप बड़े परीक्षणों पर पुनरावर्ती और भोली विधि कर सकते हैं।
डिग्री 2 ¹² की एक बहुपद पर ^, यह कार्यान्वयन 62 एमएस के लिए काम करता है, और 1800 एमएस के लिए भोली एक। अंतर स्पष्ट है।

पुनरावृत्ति से छुटकारा

प्रक्रिया को गैर-पुनरावर्ती बनाने के लिए, आपको इसके बारे में सोचना होगा। सबसे आसान तरीका है, यह मुझे लगता है, मर्जसॉर्ट (मर्ज सॉर्ट) के साथ एक सादृश्य आकर्षित करना और एक तस्वीर खींचना है जो सभी पुनरावर्ती कॉल दिखाता है:

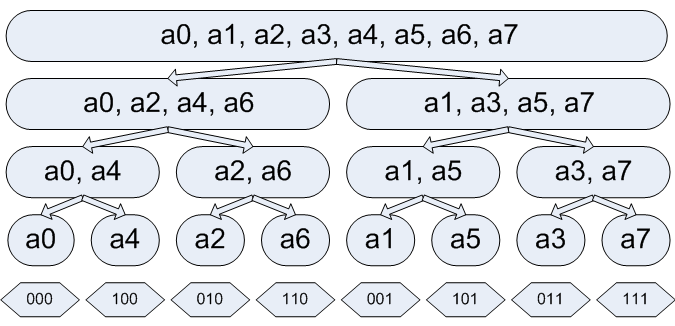
जैसा कि हम देख सकते हैं, आप एक सरणी बना सकते हैं, इसे शुरू में मानों के साथ भरें fft ( ₀ ), fft ( एक ₄ ), fft ( a ₂ ), .... यह समझना आसान है कि संख्याएँ _I एक संख्या हैं " 0 , 1 , 2 , 3 , ... " जो कि बाइनरी प्रतिनिधित्व में "विस्तारित" हैं। उदाहरण के लिए, 1 ₁ 0 = 0 0 1 ₂ , 4 ₁ 0 = 1 0 2 ₂ या 6 = 1 1 0 ₂ , 3 = 0 1 1 ₂ । आप इसे इस प्रकार समझ सकते हैं: जब पुनरावृत्ति के निचले स्तर पर उतरते हैं, तो हम एक और कम बिट (अंत से) निर्धारित करते हैं। और "सामान्य" नंबरिंग के साथ, बिट को शुरुआत से निर्धारित किया जाता है। इसलिए, आपको संख्या का "विस्तार" करने की आवश्यकता है। इसे O ( n nlog ₂ n ) के लिए "माथे" किया जा सकता है, या इसे निम्न एल्गोरिथम का उपयोग करके O ( n ) के लिए गतिशील रूप से प्रोग्राम किया जा सकता है:

0 से n - 1 तक एक चक्र चलाएं
हम स्टोर करेंगे और गतिशील रूप से नंबर की सबसे महत्वपूर्ण इकाई बिट की संख्या को पुन: लिखेंगे। यह केवल तभी बदलता है जब वर्तमान संख्या दो की शक्ति होती है: 1 से बढ़ जाती है।
जब हम किसी संख्या के सबसे महत्वपूर्ण बिट को जानते हैं, तो पूरी संख्या को फ़्लिप करना मुश्किल नहीं है: "सबसे महत्वपूर्ण बिट (XOR) को काटें", शेष (पहले से गणना की गई मूल्य) फ्लिप करें और एक "कट ऑफ" इकाई जोड़ें

अब हम एक एल्गोरिथ्म के साथ आएंगे जो हमें "चरण" से एक कदम ऊंचा पाने की अनुमति देता है। हम एक चरण में पिछले चरण से सभी मान संग्रहीत करेंगे। जैसा कि आंकड़े में स्पष्ट रूप से देखा जा सकता है, पहले के = 1 के साथ कश्मीर के ब्लॉक में डेटा को संसाधित करना आवश्यक है, और फिर यह प्रत्येक चरण के साथ दोगुना हो जाता है। हम लंबाई k के दो खंडों को संसाधित करते हैं और आउटपुट पर लंबाई 2 k का एक खंड प्राप्त करते हैं। आइए एक उदाहरण देखें कि यह कैसे पुनरावर्ती किया गया था, लेख की शुरुआत से सूत्र को याद करें और दोहराएं:

दो ब्लॉकों के विलय की प्रक्रिया की दलीलें दो वैक्टर (बेशक, संदर्भ, स्रोत और परिणाम) से होंगी, पहले ब्लॉक के प्रारंभ तत्व की संख्या (दूसरे के तुरंत बाद आती है) और ब्लॉकों की लंबाई। बेशक, यह पुनरावृत्तियों द्वारा भी किया जा सकता है - अधिक STL'nosti के लिए, लेकिन हम अभी भी इस प्रक्रिया को संक्षिप्तता के लिए मुख्य एक के अंदर स्थानांतरित करेंगे।

ब्लॉक विलय

 void fft_merge(const vcd &src, vcd &dest, int start, int len) { int p1 = start; //     int en1 = start + len; //    int p2 = start + len; //     int en2 = star + len * 2; //    int pdest = start; //      int nlen = len * 2; //    for (int i = 0; i < nlen; i++) { double alpha = 2 * M_PI * i / nlen; cd w = cd(cos(alpha), sin(alpha)); //   dest[pdest] = src[p1] + w * src[p2]; if (++p1 >= en1) p1 = start; if (++p2 >= en2) p2 = start + len; } }

और मुख्य रूपांतरण प्रक्रिया:

 vcd fft(const vcd &as) { int n = as.size(); int k = 0; //  n   while ((1 << k) < n) k++; vi rev(n); rev[0] = 0; int high1 = -1; for (int i = 1; i < n; i++) { if ((i & (i - 1)) == 0) //    .  i  ,  i-1     . high1++; rev[i] = rev[i ^ (1 << high1)]; //   rev[i] |= (1 << (k - high1 - 1)); //    } vcd cur(n); for (int i = 0; i < n; i++) cur[i] = as[rev[i]]; for (int len = 1; len < n; len <<= 1) { vcd ncur(n); for (int i = 0; i < n; i += len * 2) fft_merge(cur, ncur, i, len); cur.swap(ncur); } return cur; }

अनुकूलन

डिग्री 2 ^{1 6 के} एक बहुपद पर ^, पुनरावृत्ति 640 एमएस काम करता है ^, पुनरावृत्ति के बिना - 500. एक सुधार है, लेकिन कार्यक्रम और भी तेजी से किया जा सकता है। हम उस संपत्ति का उपयोग करते हैं जो ω _i = -ω _{i + n / 2 है} । इसलिए, हम रूट को दो बार नहीं ले सकते हैं और _i the _j - जटिल संख्याओं के साइन, कोसाइन और गुणा बहुत महंगा संचालन है।

fft_merge ()

 for (int i = 0; i < len; i++) { double alpha = 2 * M_PI * i / nlen; cd w = cd(cos(alpha), sin(alpha)); //   cd val = w * src[p2]; dest[pdest] = src[p1] + val; dest[pdest + len] = src[p1] - val; pdest++; if (++p1 >= en1) p1 = start; if (++p2 >= en2) p2 = start + len; }

इस अनुकूलन के साथ एक संक्रमण को "तितली परिवर्तन" कहा जाता है। कार्यक्रम 260 एमएस काम करना शुरू कर दिया। सफलता को मजबूत करने के लिए, आइए 1 की सभी जड़ों की गणना करें और उन्हें एक सरणी में लिखें:

fft_merge ()

 int rstep = roots.size() / nlen; //      for (int i = 0; i < len; i++) { cd w = roots[i * rstep]; cd val = w * src[p2];

एफएफटी ()

 roots = vcd(n); for (int i = 0; i < n; i++) { double alpha = 2 * M_PI * i / n; roots[i] = cd(cos(alpha), sin(alpha)); }

अब गति 78 एमएस है। पहले कार्यान्वयन की तुलना में 8 गुना अनुकूलन!

कोड अनुकूलन

वर्तमान में, सभी रूपांतरण कोड में लगभग 55 लाइनें हैं। सौ नहीं, लेकिन यह काफी है - यह छोटा हो सकता है। सबसे पहले, fft_merge में अतिरिक्त चर और संचालन के एक समूह से छुटकारा पाएं :

 void fft_merge(const vcd &src, vcd &dest, int start, int len) { int p1 = start; //int en1 = start + len; //  , .   int p2 = start + len; //int en2 = start + len * 2; //  int pdest = start; //int nlen = len * 2; //      //int rstep = roots.size() / nlen; int rstep = roots.size() / (len * 2); for (int i = 0; i < len; i++) { //cd w = roots[i * rstep]; //       //cd val = w * src[p2]; cd val = roots[i * rstep] * src[p2]; dest[pdest] = src[p1] + val; dest[pdest + len] = src[p1] - val; pdest++, p1++, p2++; //if (++p1 >= en1) p1 = start; //         2len,    len,     //if (++p2 >= en2) p2 = start + len; //  } }

अब आप fft_merge से लूप को मुख्य प्रक्रिया में स्थानांतरित कर सकते हैं (आप P2 को भी हटा सकते हैं, क्योंकि P2 = p1 + len - इसने मुझे एक छोटा समय भी दिया है। जो कि उत्सुक है, अगर मैं p1 = pdest को हटा देता हूं, तो मैं व्यक्तिगत रूप से समय लाभ को मार देता हूं) :

एफएफटी ()

 for (int len = 1; len < n; len <<= 1) { vcd ncur(n); int rstep = roots.size() / (len * 2); for (int pdest = 0; pdest < n;) { int p1 = pdest; for (int i = 0; i < len; i++) { cd val = roots[i * rstep] * cur[p1 + len]; ncur[pdest] = cur[p1] + val; ncur[pdest + len] = cur[p1] - val; pdest++, p1++; } pdest += len; } cur.swap(ncur); }

जैसा कि आप देख सकते हैं, रूपांतरण स्वयं को इतना अधिक नहीं लेता है - 17 लाइनें। बाकी सब कुछ - जड़ों की पूर्व-गणना और संख्याओं का उलटा। यदि आप काम के समय ( O ( n )log ₂ n ) O ) ( n ) के बदले कोड बचाने के लिए तैयार हैं, तो आप निम्नलिखित छह के साथ संख्याओं के प्रसार की 13 पंक्तियों को बदल सकते हैं:

Fft की शुरुआत में ()

 vcd cur(n); for (int i = 0; i < n; i++) { int ri = 0; for (int i2 = 0; i2 < k; i2++) //       ri = (ri << 1) | !!(i & (1 << i2)); //      cur[i] = as[ri]; }

नतीजतन, कोड अब इस तरह दिखता है:

 vcd fft(const vcd &as) { int n = as.size(); int k = 0; //  n   while ((1 << k) < n) k++; vector<int> rev(n); rev[0] = 0; int high1 = -1; for (int i = 1; i < n; i++) { if ((i & (i - 1)) == 0) //    .  i  ,  i-1     . high1++; rev[i] = rev[i ^ (1 << high1)]; //   rev[i] |= (1 << (k - high1 - 1)); //    } vcd roots(n); for (int i = 0; i < n; i++) { double alpha = 2 * M_PI * i / n; roots[i] = cd(cos(alpha), sin(alpha)); } vcd cur(n); for (int i = 0; i < n; i++) cur[i] = as[rev[i]]; for (int len = 1; len < n; len <<= 1) { vcd ncur(n); int rstep = roots.size() / (len * 2); for (int pdest = 0; pdest < n;) { int p1 = pdest; for (int i = 0; i < len; i++) { cd val = roots[i * rstep] * cur[p1 + len]; ncur[pdest] = cur[p1] + val; ncur[pdest + len] = cur[p1] - val; pdest++, p1++; } pdest += len; } cur.swap(ncur); } return cur; }

उलटा परिवर्तन

बिंदुओं पर बहुपद के मूल्यों को प्राप्त करना, निश्चित रूप से, अच्छा है, लेकिन फूरियर रूपांतरण बेहतर कर सकता है - इन मूल्यों का उपयोग करके बहुपद का निर्माण करने के लिए और उसी समय में! यह पता चला है कि यदि हम फूरियर रूपांतरण को एक बहुपद के गुणांक के रूप में मानों की एक सरणी में लागू करते हैं, तो परिणाम को n से विभाजित करें और सेगमेंट को 1 से n - 1 ( 0 से संख्या) में बदल दें, हम मूल बहुपद के गुणांक प्राप्त करते हैं।
यहां कोड बेहद सरल है - सब कुछ पहले से ही लिखा हुआ है। मुझे लगता है कि आप इसे संभाल सकते हैं।

सबूत

आइए हम गुणांक v ( _i ) के साथ बहुपद P ( x ) के व्युत्क्रम परिवर्तन को लागू करें (मूल बहुपद में गुणांक _{i था} ):
v _i = a ₀ + ω _i a ₁ + a ₂ _i a ₂ + a _{3 i} a + ...
रूपांतरण के परिणाम पर नजर डालते हैं:
b _i = v ₀ + ω _i v ₁ + v ₂ _i v ₂ + v ₃ _i v ₃ + ...
हम v _j के मानों को _{बदलते हैं} (याद रखें कि ω ω _b = _{+ a + b m o d n} :

अब एक उल्लेखनीय तथ्य सिद्ध करते हैं: x prove 0 , ω ₀ + ω _x + _{x 2 x} + ... + _{1 ( n - 1 ) x} = 0 के लिए ।
यह इस तथ्य के समान सिद्ध होता है कि जड़ों का योग शून्य है: हम similar योग से निरूपित करते हैं, दोनों पक्षों को sides _{x से} गुणा करते हैं और देखते हैं कि क्या हुआ।
अब इस तथ्य को b _i के मान की गणना पर लागू करते हैं। ध्यान दें कि _{n - i} को छोड़कर सभी लाइनें शून्य पर रीसेट हो जाएंगी।

इस तरह से:

b _i = a _{n - i} ⋅ (= ₀ + - ₀ + + ₀ + ω ₀ + ... )

b _i = a _{n - i -} n

जिसे सिद्ध करना आवश्यक था।

आवेदन

आम तौर पर बोलते हुए, मैंने पहले से ही लेख की शुरुआत में आवेदन के बारे में थोड़ा बात की थी। विशेष रूप से, अब बहुपद का गुणन निम्न प्रकार से किया जा सकता है:

बहुपद का तेज गुणा

 vcd a, b; //  //   vcd a_vals = fft(a); vcd b_vals = fft(b); vcd c_vals(a_vals.size()); for (int i = 0; i < a_vals.size(); i++) c_vals[i] = a_vals[i] * b_vals[i]; vcd c = fft_rev(c_vals); //

यह देखना आसान है कि इस प्रोग्राम का रनिंग टाइम O ( n nlog ₂ n ) है और सबसे ज्यादा समय लेने वाला ऑपरेशन फूरियर ट्रांसफॉर्म हैं। आप यह भी देख सकते हैं कि अगर हमें दो बहुपदों के साथ अधिक जटिल अभिव्यक्ति की गणना करने की आवश्यकता है, तो हम अभी भी केवल तीन परिवर्तन कर सकते हैं - इसके अलावा और घटाव भी रैखिक समय में काम करेगा। दुर्भाग्य से, विभाजन इतना सरल नहीं है, क्योंकि एक बहुपद गलती से किसी बिंदु पर 0 मान ले सकता है। UPD2: यह मत भूलो कि डिग्री एन के दो बहुपद के उत्पाद की संख्या 2n होगी, इसलिए प्रवेश करते समय, आपको "अतिरिक्त" शून्य अग्रणी गुणांक जोड़ना चाहिए।
यदि आप गुणांक - अंकों के साथ बहुपद के रूप में दशमलव (या अधिक) संख्या प्रणाली में एक संख्या का प्रतिनिधित्व करते हैं, तो लंबी संख्याओं का गुणन भी बहुत जल्दी किया जा सकता है।
और अंत में, जो कार्य मैं अगली पोस्ट में विश्लेषण करूंगा: आपके पास अक्षर A, T, G, C. से एक ही लंबाई के क्रम 1 0 ⁵ की दो पंक्तियाँ हैं। इनमें से किसी एक पंक्ति की चक्रीय पारी खोजना आवश्यक है, ताकि वर्णों की अधिकतम संख्या मेल खाए। जाहिर है O ( n ² ) के लिए एक भोली समाधान, लेकिन FFT का उपयोग करके एक समाधान है।
सौभाग्य है

UPD: मैंने पास्टबिन पर पूरा कोड पोस्ट किया है

फूरियर रूपांतरण का उपयोग कर बहुपद का बहुगुणना आसान है

परिभाषाएँ और उपयोग

जटिल संख्या

1 की जटिल जड़ें

जड़ों का योग शून्य क्यों है

यह कैसे काम करता है

कुछ लिखो

धीमे धीमे

पुनरावृत्ति से छुटकारा

ब्लॉक विलय

अनुकूलन

fft_merge ()

fft_merge ()

एफएफटी ()

कोड अनुकूलन

एफएफटी ()

Fft की शुरुआत में ()

उलटा परिवर्तन

सबूत

आवेदन

बहुपद का तेज गुणा

More articles: