छवि प्रसंस्करण पर हाल के लेखों के प्रकाश में, मैं समोच्च एल्गोरिदम के बारे में थोड़ी बात करना चाहूंगा: रॉबर्ट्स, प्रीविट और सोबेल विधियों (इन विधियों को सबसे प्रसिद्ध और अक्सर उपयोग के रूप में विचार के लिए लिया जाता है)।
मैं वॉल्यूम सिद्धांत के साथ परेशान नहीं करूंगा, लेकिन मैं खुद को केवल एल्गोरिदम के सार को समझने के लिए आवश्यक न्यूनतम जानकारी तक सीमित कर दूंगा।
ये सभी विधियां चमक संकेत के मूल गुणों में से एक पर आधारित हैं -
असंतोष । अंतराल की खोज करने का सबसे आम तरीका एक
चलती हुई मुखौटा का उपयोग करके छवि को संसाधित करना है, जिसे एक
फिल्टर, कोर, विंडो या टेम्पलेट भी कहा जाता है, जो मूल छवि के पिक्सल के निर्दिष्ट समूह के अनुरूप एक प्रकार का वर्ग मैट्रिक्स है। मैट्रिक्स तत्वों को
गुणांक कहा जाता
है । कुछ स्थानीय परिवर्तनों में ऐसे मैट्रिक्स का संचालन करना
फ़िल्टरिंग या
स्थानिक फ़िल्टरिंग कहा जाता है।
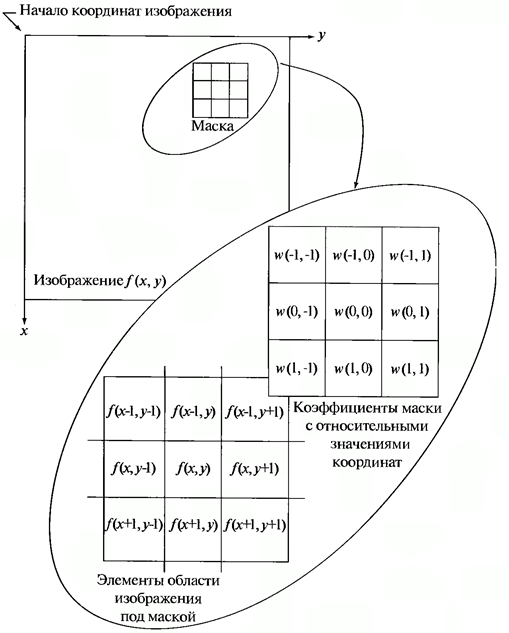
स्थानिक फ़िल्टरिंग योजना नीचे दिए गए चित्र में चित्रित की गई है (चित्र 1 देखें)।
चित्रा 1. स्थानिक फ़िल्टरिंग योजना
प्रक्रिया केवल छवि से बिंदु तक फिल्टर मास्क को स्थानांतरित करने पर आधारित है; प्रत्येक बिंदु (x, y) पर, पूर्वनिर्धारित संबंधों का उपयोग करके फ़िल्टर प्रतिक्रिया की गणना की जाती है। रैखिक स्थानिक फ़िल्टरिंग के मामले में, फ़िल्टर मुखौटा द्वारा कवर किए गए क्षेत्र में संबंधित पिक्सेल मूल्यों द्वारा फ़िल्टर गुणांक के उत्पाद के योग द्वारा प्रतिक्रिया निर्दिष्ट की जाती है। चित्र 1 में दिखाए गए तत्व के 3x3 मास्क के लिए
, छवि के बिंदु
(x, y) पर रैखिक फ़िल्टरिंग का परिणाम (प्रतिक्रिया)
R होगा:
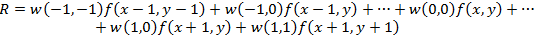(1.1)जो, जैसा कि आप देख सकते हैं, मुखौटा के तहत पिक्सेल मानों द्वारा मास्क गुणांक के उत्पादों का योग है। विशेष रूप से, हम ध्यान दें कि गुणांक
w (0,0) f (x, y) पर खड़ा है, यह दर्शाता है कि मुखौटा बिंदु
(x, y) पर केंद्रित है।
चमक में अंतर का पता लगाने पर, पहले और दूसरे क्रम के डेरिवेटिव के असतत एनालॉग का उपयोग किया जाता है। सादगी के लिए, एक आयामी डेरिवेटिव पर विचार किया जाएगा।
एक आयामी फ़ंक्शन
f (x) के पहले व्युत्पन्न को पड़ोसी तत्वों के मूल्यों के बीच अंतर के रूप में परिभाषित किया गया है:
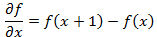(1.2)यहां हमने आंशिक व्युत्पन्न के रूप में संकेतन का उपयोग दो चर
च (x, y) के मामले में उसी संकेतन को संरक्षित करने के लिए किया है, जहां हमें दो स्थानिक अक्षों के साथ आंशिक व्युत्पत्ति से निपटना है। आंशिक व्युत्पन्न का उपयोग विचार के पदार्थ को नहीं बदलता है।
इसी तरह, दूसरे व्युत्पन्न को पहले व्युत्पन्न के आसन्न मूल्यों के अंतर के रूप में परिभाषित किया गया है:
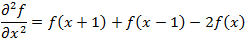(1.3)डिजिटल छवि के पहले व्युत्पन्न की गणना दो आयामी ढाल के विभिन्न असतत सन्निकटन पर आधारित है। परिभाषा के अनुसार, बिंदु पर छवि ढाल
f (x, y) (x, y) एक वेक्टर है [2]:
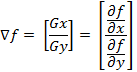(1.4)जैसा कि गणितीय विश्लेषण के पाठ्यक्रम से जाना जाता है, ग्रेडिएंट वेक्टर की दिशा बिंदु
(x, y) [2] में फ़ंक्शन
च के परिवर्तन की अधिकतम दर की दिशा के साथ मेल खाती है।
इस वेक्टर के मॉड्यूल द्वारा
कंट्रोस का पता लगाने में एक महत्वपूर्ण भूमिका निभाई जाती है, जिसे
andf द्वारा दर्शाया जाता है और इसके बराबर होता है
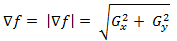(1.5)यह मान बिंदु
(x, y) पर फ़ंक्शन
च के परिवर्तन की अधिकतम दर के मूल्य के बराबर है, और अधिकतम वेक्टर
.f की दिशा में पहुंच गया है।
∇f को अक्सर ढाल भी कहा जाता है।
ग्रेडिएंट वेक्टर की दिशा भी एक महत्वपूर्ण विशेषता है।
Α (x, y) बिंदु
(x, y) और
x अक्ष पर वेक्टर
thef की दिशा के बीच
का कोण। जैसा कि गणितीय विश्लेषण से जाना जाता है [2],
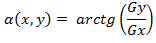(1.6)यहां से बिंदु
(x, y) पर समोच्च की दिशा का पता लगाना आसान है, जो इस बिंदु पर ढाल वेक्टर की दिशा के लंबवत है। और आप प्रत्येक बिंदु के लिए आंशिक डेरिवेटिव
∂f / ∂x और
∂f / eachy की गणना करके छवि ढाल की गणना कर सकते हैं।
रॉबर्ट्स ऑपरेटर
नीचे दिए गए चित्र में दिखाए गए 3x3 क्षेत्र को (चित्र 2 देखें) एक निश्चित छवि तत्व के आसपास के क्षेत्र में चमक मूल्यों का प्रतिनिधित्व करते हैं।
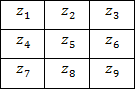चित्र 2. पड़ोसन 3x3 छवि के अंदर
एक बिंदु पर पहला आंशिक डेरिवेटिव खोजने के लिए सबसे सरल तरीकों में से एक
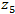
निम्नलिखित रॉबर्ट्स क्रॉस ग्रेडिएंट ऑपरेटर को लागू करने में शामिल हैं [1]:
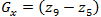(1.7)और
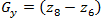(1.8)इन व्युत्पत्तियों को चित्र 3 में मास्क द्वारा वर्णित ऑपरेटर का उपयोग करके पूरी छवि को संसाधित करके महसूस किया जा सकता है, पहले वर्णित फ़िल्टरिंग प्रक्रिया का उपयोग करके।
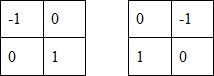चित्रा 3. रॉबर्ट्स ऑपरेटर मास्क
2x2 मास्क का कार्यान्वयन बहुत सुविधाजनक नहीं है, क्योंकि उनके पास स्पष्ट रूप से परिभाषित केंद्रीय तत्व नहीं है, जो फ़िल्टरिंग के परिणाम को महत्वपूर्ण रूप से प्रभावित करता है। लेकिन यह "माइनस" इस एल्गोरिथम की एक बहुत ही उपयोगी संपत्ति उत्पन्न करता है - उच्च छवि प्रसंस्करण गति।
प्रिटिट ऑपरेटर
प्रीविट ऑपरेटर, रॉबर्ट्स ऑपरेटर की तरह, चित्र 2 में दिखाए गए 3x3 छवि क्षेत्र से संचालित होता है, केवल इस तरह के मास्क का उपयोग अन्य अभिव्यक्तियों द्वारा निर्दिष्ट किया जाता है:
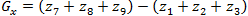(1.9)और
(1.10)इन योगों में, 3x3 पड़ोस की ऊपरी और निचली पंक्तियों के साथ रकम के बीच का अंतर
x अक्ष के साथ व्युत्पन्न का अनुमानित मूल्य है, और इस पड़ोस के पहले और आखिरी कॉलम के साथ रकम के बीच का अंतर
y अक्ष के साथ व्युत्पन्न है। इन सूत्रों को लागू करने के लिए, मास्क 4 द्वारा वर्णित ऑपरेटर, जिसे प्रीविट ऑपरेटर कहा जाता है, का उपयोग किया जाता है।
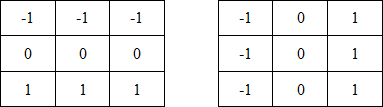चित्रा 4. Previtt ऑपरेटर मास्क
सोबेल ऑपरेटर
सोबेल ऑपरेटर चित्रा 2 में दिखाए गए 3x3 छवि क्षेत्र का भी उपयोग करता है। यह प्रीविट ऑपरेटर के समान है, और संशोधन में मध्यम तत्वों के लिए 2 के वजन कारक का उपयोग होता है:
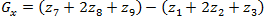(1.11)और
(1.12)इस बढ़े हुए मूल्य का उपयोग मिडपॉइंट्स को अधिक वजन देकर चौरसाई प्रभाव को कम करने के लिए किया जाता है।
सोबेल ऑपरेटर द्वारा उपयोग किए जाने वाले मुखौटे नीचे चित्र में प्रदर्शित किए गए हैं (चित्र 5 देखें)।
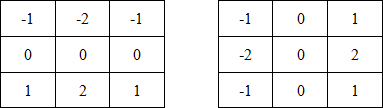चित्रा 5. सोबेल ऑपरेटर मास्क
ऊपर चर्चा किए गए मुखौटे का उपयोग ढाल के घटकों को प्राप्त करने के लिए किया जाता है
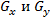
। ढाल के परिमाण की गणना करने के लिए, इन घटकों को एक साथ उपयोग किया जाना चाहिए:
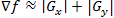(1.14)या
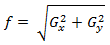(1.15)खैर, अंत में, मैं वर्णित विधियों का उपयोग करके छवि प्रसंस्करण के परिणाम (आंकड़े 6-8 देखें) प्रदर्शित करूंगा।
चित्र 6. मूल छवि संख्या 1
चित्र 7. मूल छवि संख्या 2
चित्र 8. मूल छवि संख्या 3
रॉबर्ट्स, प्रीविट और सोबेल के तरीकों से प्रसंस्करण परिणाम नीचे दिखाए गए हैं:
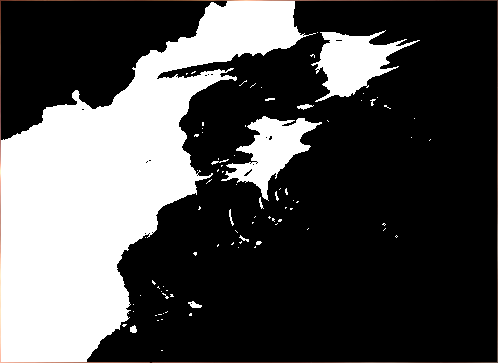चित्र 9. रॉबर्ट्स विधि द्वारा प्रसंस्करण के बाद मूल चित्र
चित्र 10 Prewitt विधि द्वारा प्रसंस्करण के बाद मूल चित्र
चित्र 11. सोबेल विधि द्वारा प्रसंस्करण के बाद मूल चित्र
संदर्भ
- आर। गोंजालेज, आर। वुड्स डिजिटल इमेज प्रोसेसिंग - एम: टेक्नोस्फीयर, 2005 - 1007 एस
- कुद्रीवत्सेव एल.वी. गणितीय विश्लेषण में एक लघु पाठ्यक्रम - एम ।: नौका, 1989 - 736
- अनिसिमोव बी.वी. मान्यता और डिजिटल इमेज प्रोसेसिंग - एम ।: उच्च। स्कूल, 1983 - 295s