🏀 👺 👨‍🎨 कैनी समोच्च एल्गोरिथ्म पर टिप्पणी 👩‍👩‍👦 👰🏽 👩🏿‍🍳

अमूर्त

कैनी बाउंड्री डिटेक्टर लेख में, जैसा कि मैंने पहले ही टिप्पणियों में लिखा है, एल्गोरिथ्म का सार विकृत है और उस स्थान पर खो गया है जहां ग्रेडिएंट की खोज की गई है। इसके लिए, सोबेल की गुठली का उपयोग किया जाता है, जिसके बारे में कैनी ने कुछ भी नहीं कहा। मैंने एक सुधार लिखा है जो समोच्च एल्गोरिथ्म को तेजी से काम करने की अनुमति देगा। इसके अलावा, इस लेख को छवि ढाल के बारे में लेखन की निरंतरता माना जा सकता है ।
लेख चिकनाई कोर के इष्टतम विवेकाधिकार कदम की पसंद के साथ मुद्दों को संबोधित नहीं करता है।

आवश्यक शर्तें

छवि चमक फ़ंक्शन के ग्रेडिएंट की गणना करने से पहले, अक्सर, एक स्थिर परिणाम प्राप्त करने के लिए, वे गॉसियन फ़िल्टर का उपयोग करके शोर फ़िल्टरिंग का सहारा लेते हैं, अर्थात, वे प्रारंभिक स्नेहन करते हैं।
फिर, डेरिवेटिव के अंतर सन्निकटन का उपयोग करके, ढाल घटक पाए जाते हैं।

चलो स्नेहन को NxN बिंदुओं के आकार का उपयोग करके किया जाता है, और कुल्हाड़ियों के साथ डेरिवेटिव की गणना करने के लिए अंतर टेम्पलेट 1xK और Kx1 हैं । छवि का आकार MxM के बराबर सेट है।
सरलता के लिए, हम केवल गुणन पर विचार करेंगे, फिर अनुक्रम "Smaz-> Gradient" को N ^ 2 * M ^ 2 + 2 * K * M ^ 2 = (N ^ 2 + 2 * K) * M ^ 2 संचालन की आवश्यकता होगी।

हालाँकि, ज्ञात सूत्र

जिसके उपयोग से हमें परिमाण के आदेशों द्वारा संख्या को कम करने की अनुमति मिलेगी। वह किस बारे में बात कर रही है? - इस तथ्य के बारे में कि, सिद्धांत रूप में, पहले स्नेहन प्रदर्शन करना और फिर छवि को अलग करना आवश्यक नहीं है। आप च की कोर को अलग कर सकते हैं च और फिर दृढ़ संकल्प। चलिए शुरू करते हैं।

कर्नेल जुदाई

आइए दो आयामी गॉस फ़ंक्शन को देखें:

x के संबंध में इसकी व्युत्पत्ति निम्नानुसार लिखी गई है:

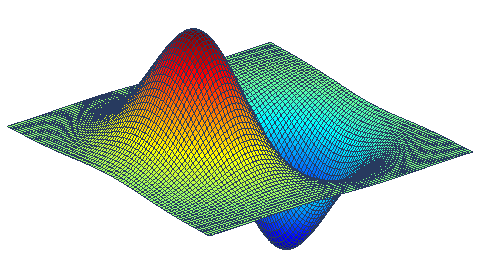
हम इस शानदार व्युत्पत्ति को MatLab के कोड को निष्पादित करके प्राप्त कर सकते हैं:

sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .

sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .

sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .

इस तरह के कर्नेल के साथ एक फिल्टर को कभी-कभी कैनी फिल्टर कहा जाता है, और कर्नेल को कैनी कर्नेल कहा जाता है, जो अन्य ऑपरेटरों के साथ व्युत्पन्न का अनुमान लगाता है। इस अवसर पर, मैं एक उल्लेखनीय सचित्र नोट साझा करता हूं।

ध्यान दें कि व्युत्पन्न निर्देशांक द्वारा वियोज्य है, जिसका अर्थ है कि हम एक धुंधली छवि के ढाल की गणना के लिए एक पंक्ति-स्तंभ एल्गोरिथ्म को लागू कर सकते हैं:

हम एक पंक्ति-कॉलम एल्गोरिथ्म के मामले में संचालन की संख्या की गणना करते हैं।

Y के संबंध में व्युत्पन्न प्राप्त करने के लिए:

हम आकार 1xK1 की विंडो द्वारा पंक्तियों में एक गाऊसी छवि I की प्रक्रिया करते हैं , हमें K * M ^ 2 गुणन के लिए एक छवि I1 मिलती है (कर्नेल को सामान्य करने के लिए मत भूलना);
हम छवि I1 को पंक्तियों में K1x1 आकार के कर्नेल के साथ संसाधित करते हैं :

(कर्नेल विवेकाधीन चरणों को चुनना न भूलें ताकि नमूनों का योग 0 के बराबर हो)
इस तरह के एक ऑपरेशन के लिए, हमें कई की जरूरत है - के * एम ^ 2 गुणा।

एक्स के संबंध में व्युत्पन्न प्राप्त करने के लिए एल्गोरिथ्म समान है, और हमें प्राप्त होने वाले संचालन की संख्या को संक्षेप में कहें, धुंधले ढाल के घटकों की गणना करने के लिए, हमें 4 * के 1 * एम ^ 2 की आवश्यकता है।

प्रभावशीलता

वर्णित अनुकूलन की प्रभावशीलता को अनुपात द्वारा निर्धारित किया जा सकता है:

यह पता चला कि प्रभावशीलता केवल खिड़कियों के आकार पर निर्भर करती है, लेकिन छवियों के आकार पर नहीं।
आकार N = 5 का कर्नेल सरल एल्गोरिथ्म में स्नेहन के लिए उपयोग किया जाता है, और पहले क्रम सन्निकटन (गुठली [-1 1] और [-1 1] ') - K = 2 का उपयोग डेरिवेटिव की गणना करने के लिए किया जाता है।

एक अनुकूलित पंक्ति-कॉलम एल्गोरिथ्म के मामले में, हम K1 = 5. तब λ = 20/29 = 0.68 सेट करते हैं।
दक्षता λ <1 - हम अनुक्रम "चिकनाई-ढाल" की गणना करते समय अंकगणितीय संचालन की संख्या को कम करने में कामयाब रहे।

कैनी समोच्च एल्गोरिथ्म पर टिप्पणी

अमूर्त

आवश्यक शर्तें

कर्नेल जुदाई

प्रभावशीलता

More articles: