परिचय
खेल और एप्लिकेशन प्रोग्रामिंग में RMQ समस्या बहुत आम है। यह आश्चर्यजनक है कि किसी ने भी इस दिलचस्प विषय का हब्रे पर उल्लेख नहीं किया है। मैं अंतर को भरने की कोशिश करूंगा।
संक्षिप्त नाम RMQ रेंज ऐरे में एक खंड पर न्यूनतम (अधिकतम) क्वेरी के लिए न्यूनतम रेंज (अधिकतम) क्वेरी के लिए है। निश्चितता के लिए, हम न्यूनतम लेने के संचालन पर विचार करेंगे।
एक सरणी A [1..n] दी जाए। हमें फॉर्म के एक अनुरोध का जवाब देने में सक्षम होना चाहिए "ईथ तत्व से जेठ के लिए अंतराल में न्यूनतम खोजें"।
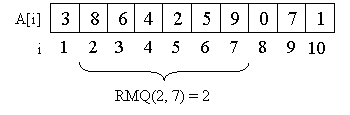
एक उदाहरण के रूप में, एक सरणी A = {3, 8, 6, 4, 2, 5, 9, 0, 7, 1} पर विचार करें।
उदाहरण के लिए, सातवें के माध्यम से दूसरे तत्व से खंड पर न्यूनतम दो के बराबर है, वह है, आरएमक्यू (2, 7, = 2)।
स्पष्ट निर्णय दिमाग में आता है: हम प्रत्येक अनुरोध का उत्तर केवल उस सरणी के सभी तत्वों पर जाकर देखेंगे जो हमें उस खंड पर झूठ हैं जिसकी हमें ज़रूरत है। इस तरह का एक समाधान, हालांकि, सबसे प्रभावी नहीं है। दरअसल, सबसे खराब स्थिति में, हमें ओ (एन) तत्वों पर जाना होगा, अर्थात। इस एल्गोरिथ्म का समय जटिलता अनुरोध के अनुसार O (n) है। हालाँकि, समस्या को अधिक कुशलता से हल किया जा सकता है।
समस्या कथन
सबसे पहले, हम समस्या के कथन को स्पष्ट करते हैं।
लेख शीर्षक में
स्थिर शब्द का क्या अर्थ है? आरएमक्यू का कार्य कभी-कभी किसी सरणी के तत्वों को बदलने की क्षमता के साथ उत्पन्न होता है। यही है, एक तत्व को बदलने की क्षमता, या यहां तक कि एक खंड में तत्वों को बदलने की क्षमता (उदाहरण के लिए, उप-खंड में सभी तत्वों को 3 से बढ़ाएं) न्यूनतम लेने के अनुरोध में जोड़ा जाता है। समस्या का यह संस्करण, जिसे
गतिशील RMQ कहा जाता है, मैं बाद के लेखों में विचार करूंगा।
मैं यहां ध्यान देता हूं कि RMQ कार्य
ऑफ़लाइन और
ऑनलाइन संस्करणों में विभाजित है।
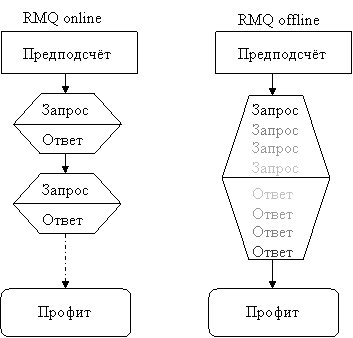
ऑफ़लाइन विकल्प में, आप पहले सभी अनुरोध प्राप्त कर सकते हैं, उन्हें किसी तरह से विश्लेषण कर सकते हैं, और उसके बाद ही उन्हें जवाब दे सकते हैं। एक
ऑनलाइन बयान में, अनुरोध बदले में दिए जाते हैं, अर्थात अगला अनुरोध पिछले एक के जवाब के बाद ही आता है। ध्यान दें कि
ऑनलाइन इंस्टालेशन में आरएमक्यू को हल करने के बाद, हम तुरंत
ऑफलाइन आरएमक्यू के लिए एक समाधान प्राप्त करते हैं, हालांकि,
ऑफ़लाइन आरएमक्यू के लिए एक अधिक प्रभावी समाधान हो सकता है जो
ऑनलाइन इंस्टॉलेशन के लिए लागू नहीं है।
इस लेख में हम
स्थैतिक ऑनलाइन RMQ को देखेंगे।
प्रीप्रोसेसिंग टाइम
एल्गोरिथ्म की प्रभावशीलता का मूल्यांकन करने के लिए, हम एक और समय विशेषता का परिचय देते हैं - प्रीप्रोसेसिंग समय। इसमें, हम तैयारी के लिए समय को ध्यान में रखेंगे, अर्थात्। अनुरोधों का जवाब देने के लिए आवश्यक कुछ जानकारी की पूर्व-गणना।
ऐसा लगता है, हमें प्रीप्रोसेसिंग को अलग से अलग करने की आवश्यकता क्यों है? लेकिन क्यों। हम समस्या का एक और समाधान देते हैं।
इससे पहले कि आप प्रश्नों का उत्तर देना शुरू करें, प्रत्येक सेगमेंट के उत्तर को लें और सीधे गणना करें! यानी हम एक सरणी P [n] [n] का निर्माण करेंगे (भविष्य में मैं C- जैसे सिंटैक्स का उपयोग करूंगा, हालांकि मैं कार्यान्वयन में आसानी के लिए एक से एक सरणी A को संख्या दूंगा), जहां P [i] [j] I से j तक के अंतराल में न्यूनतम बराबर होगा। और हम इस सरणी को कम से कम O (n
3 ) के लिए गिनते हैं - सबसे बेवकूफ तरीके से, प्रत्येक खंड के लिए सभी तत्वों पर जा रहे हैं। हम ऐसा क्यों कर रहे हैं? मान लीजिए कि प्रश्नों की संख्या n
3 से बहुत अधिक है। तब हमारे एल्गोरिथ्म का कुल ऑपरेटिंग समय हे (n
3 ) + q * O (1) = O (q), अर्थात। प्रीप्रोसेसिंग के लिए समय और बड़े एल्गोरिथ्म के समग्र समय को प्रभावित नहीं करेगा। लेकिन जानकारी के लिए धन्यवाद, हमने O (n) के बजाय O (1) समय में अनुरोध का जवाब देना सीखा। यह स्पष्ट है कि O (q) O (qn) से बेहतर है।
दूसरी ओर, q <n
3 के लिए , प्रीप्रोसेसिंग समय एक भूमिका निभाएगा, और उपरोक्त एल्गोरिथ्म में यह O (n
3 ) है - दुर्भाग्य से, यह बहुत लंबा है, भले ही इसे कम किया जा सकता है (सोचें कि कैसे) O (एन
२ )।
इस क्षण से शुरू करके, हम एल्गोरिथ्म के अस्थायी विशेषताओं को निरूपित करते हैं (पी (एन), क्यू (एन)), जहां पी (एन) पूर्व-गणना का समय है और क्यू (एन) एक अनुरोध का जवाब देने का समय है।
तो, हमारे पास दो एल्गोरिदम हैं। एक (O (1), O (n)), दूसरा (O (n
2 ), O (1)) के लिए काम करता है। हम सीखते हैं कि (O (nlogn), O (1)) में समस्या को कैसे हल किया जाए, जहाँ logn n का बाइनरी लॉगरिथम है।
गीतात्मक विषयांतर। ध्यान दें कि आप किसी भी संख्या को लघुगणक के आधार के रूप में ले सकते हैं, क्योंकि लॉग एन हमेशा लॉग
बी से भिन्न होता है एन बिल्कुल ठीक समय की एक निरंतर संख्या। स्कूल बीजगणित पाठ्यक्रम से याद करते हुए निरंतर, बी लॉग
है ।
तो, हम अगले कदम के लिए मिला:
विरल तालिका, या विरल तालिका
विरल सारणी एक सारणी है ST [] [] ऐसा है कि ST [k] [i] अर्ध-अंतराल [A [i], A [i + २
k ] पर न्यूनतम है। दूसरे शब्दों में, इसमें सभी खंडों पर मिनीमा होता है जिसकी लंबाई दो की शक्ति होती है।
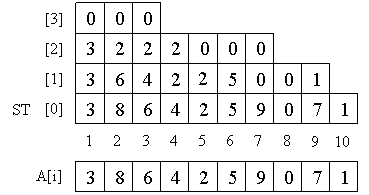
हम सरणी एसटी [के] [i] को निम्नानुसार गिनते हैं। यह स्पष्ट है कि एसटी [0] सिर्फ हमारा ए। ए। अगला है, हम स्पष्ट संपत्ति का उपयोग करते हैं:
ST [k] [i] = min (ST [k-1] [i], ST [k-१] [i + २
k - १ ])। उसके लिए धन्यवाद, हम पहले ST [1], फिर ST [2] आदि की गणना कर सकते हैं।
ध्यान दें कि हमारी तालिका में O (nlogn) तत्व हैं, क्योंकि स्तर संख्या logn से अधिक नहीं होनी चाहिए, क्योंकि k के बड़े मानों के लिए आधे-अंतराल की लंबाई पूरे सरणी की लंबाई से अधिक लंबी हो जाती है और इससे संबंधित मानों को संग्रहीत करने का कोई मतलब नहीं होता है। और प्रत्येक स्तर ओ (एन) तत्वों पर।
फिर से लयात्मक विषयांतर: यह नोटिस करना आसान है कि हमारे पास अभी भी सरणी के कई अप्रयुक्त तत्व हैं। क्या यह इसके लायक है कि टेबल को अलग से स्टोर करें ताकि मेमोरी बर्बाद न हो? हम अपने कार्यान्वयन में अप्रयुक्त मेमोरी की मात्रा का अनुमान लगाते हैं। अप्रयुक्त तत्वों की i-th पंक्ति पर - 2
i - 1. इसलिए, 2 (2
i - 1) = O (2
logn ) = O (n) कुल अप्रयुक्त रहता है, अर्थात, किसी भी स्थिति में, हमें आदेश O (nlogn) की आवश्यकता होती है - O (n) = O (nlogn) स्पार्स टेबल को स्टोर करने के लिए स्थान। इसलिए आप अप्रयुक्त वस्तुओं के बारे में चिंता नहीं कर सकते।
और अब मुख्य प्रश्न: हमने यह सब क्यों माना? ध्यान दें कि सरणी का कोई भी खंड लंबाई के दो अतिव्यापी उप-खंडों में विभाजित है।

हमें RMQ (i, j) की गणना के लिए एक सरल सूत्र मिलता है। यदि k = log (j - i + 1), तो RMQ (i, j) = min (ST (i, k), ST (j - 2
k + 1, k))। इस प्रकार, हम एल्गोरिथ्म को (O (nlogn), O (1)) प्राप्त करते हैं। हुर्रे!
... लगभग मिलता है। हम O (1) के लिए जाने का लघुगणक कैसे लेते हैं? इसकी गणना करने का सबसे आसान तरीका सभी मूल्यों के लिए भी है जो n से अधिक नहीं है। यह स्पष्ट है कि प्रीप्रोसेसिंग का स्पर्शोन्मुख व्यवहार इससे नहीं बदलेगा।
आगे क्या है?
और बाद के लेखों में, हम इस कार्य के कई रूपों और उनसे जुड़े भूखंडों पर विचार करेंगे, जैसे:
- खंडों का वृक्ष
- अंतराल संशोधन
- खंडों का दो आयामी वृक्ष
- आसन्न RSQ समस्या
- फेनविक वृक्ष
- LCA कार्य
- RMQ समस्या का लगातार बयान
- ... बहुत सारी रोचक बातें ...
- और सबसे आकर्षक बात: फराह-कोल्टन और बेंडर एल्गोरिथ्म और परिवर्तन RMQ -> LCA -> RMQ us 1, जो हमें RMQ समस्या को हल करने की अनुमति देता है (O (n), O (1))
विवरण के लिए, आप संपर्क कर सकते हैं, उदाहरण के लिए, T. Cormen, C. Leiserson, और R. Rivest की चतुर पुस्तक में "एल्गोरिथम: निर्माण और विश्लेषण।"
अन्य विषय बाद के विषयों में दिखाई देंगे।
आपका ध्यान देने के लिए धन्यवाद।