ग्राफ दृश्य। रिब बाइंडिंग विधि

कभी-कभी ग्राफ को ग्राफिकल रूप में प्रस्तुत करना उपयोगी होता है ताकि संरचना दिखाई दे। ऐसे दर्जनों उदाहरण हैं जहां यह काम आ सकता है: वर्गों के पदानुक्रम का दृश्य और किसी कार्यक्रम के स्रोत कोड के पैकेज, एक सामाजिक ग्राफ (उसी ट्विटर या फेसबुक) या विज़ुअलाइज़ेशन ग्राफ़ (जो प्रकाशन किसके लिए संदर्भित हैं) का दृश्य, आदि। लेकिन यहाँ समस्या यह है: ग्राफ़ में किनारों की संख्या अक्सर इतनी बड़ी होती है कि खींचा गया ग्राफ़ बस पार्स करना असंभव है। इस तस्वीर को देखिए:



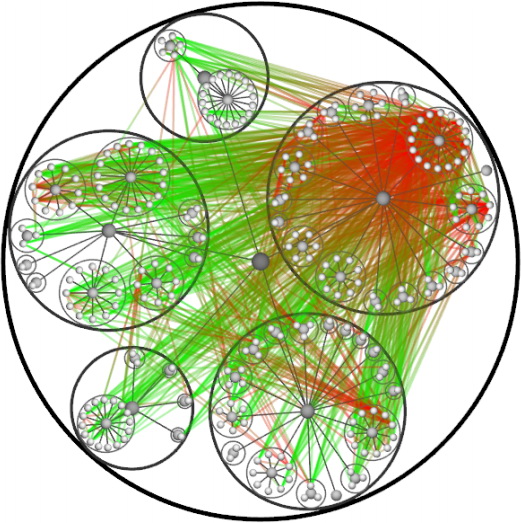
यह कुछ सॉफ्टवेयर सिस्टम का एक निर्भरता ग्राफ है। यह पेकेटाइजेशन (ग्रे बॉल्स - पैकेज, व्हाइट बॉल्स - क्लासेस) का एक पेड़ है, जिस पर दूसरों पर कुछ वर्गों की निर्भरता के किनारों को लगाया जाता है। दिशा तीरों को न खींचने के लिए, किनारों को ढाल रेखाओं के रूप में खींचा जाता है, जहां हरे रंग की शुरुआत होती है और लाल किनारे का अंत होता है। जैसा कि आप देख सकते हैं, ग्राफ़ इतना अधिक ओवरलोडेड है कि कार्यक्रम की वास्तुकला का पता नहीं लगाया जा सकता है।
इस समस्या को हल करने वाली विधि के बिल्ली विवरण के तहत।

विधि का वर्णन

विधि का विचार शानदार ढंग से सरल है - केबल नेटवर्क में समान सिद्धांत का उपयोग क्यों नहीं किया जाता है? हम में से बहुत से लोग जानते हैं कि बहुत सारे तार होने पर कौन सी गड़बड़ शुरू होती है। इस गंदगी को रोकने के लिए, तारों को बांध दिया जाता है।
इस विचार को ग्राफ़ पर कैसे लागू करें और एल्गोरिदम को लागू करें?

एक उदाहरण का उपयोग करके एक किनारे को खींचने के उदाहरण पर विचार करें। यह शीर्ष पी ₀ से शिखर पी ₄ तक एक छोर खींचना आवश्यक है:



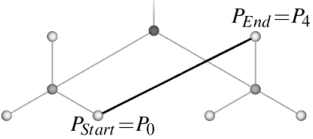
इन चोटियों के बीच का रास्ता खोजें:



अब अंक ₀ , P ₁ , P ₂ , P ₃ , P ₄ : द्वारा बनाए गए बहुभुज के माध्यम से एक वक्र बनाएं।



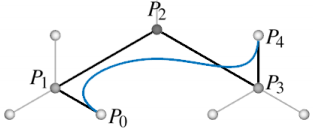
वास्तव में, यह कैसे करना है? इस पद्धति के लेखकों ने विश्लेषण किया है कि विज़ुअलाइज़ेशन उद्देश्यों के लिए टुकड़े के रूप में परिभाषित क्यूबिक बी-स्प्लिन सबसे उपयुक्त हैं। ऐसे बी-स्प्लिन को खोजने की समस्या शास्त्रीय है और लंबे समय तक दूसरों द्वारा हल की गई है। संक्षेप में, मैं सिर्फ इतना ही कहूंगा कि एक क्यूबिक बी-स्पलाइन दो-आयामी अंतरिक्ष में तीसरे क्रम के घटता का एक संग्रह है, जिसके लिए किनारों पर पहले और दूसरे डेरिवेटिव के लिए मिलान की स्थिति संतुष्ट है। यदि कोई इस पद्धति को लागू करना चाहता है, तो पहिया को फिर से न करें - अंत में मैंने सी # में किनारों को प्रस्तुत करने के लिए काम करने वाला कोड पोस्ट किया।
पसलियों की संयोजकता की डिग्री को नियंत्रित करने के लिए, एक पैरामीटर degree पेश किया जाता है जो 0 से 1 तक मान लेता है (0 - पसलियों को एक बंडल में नहीं जोड़ा जाता है और स्वतंत्र सीधी रेखाएं हैं, 1 - पसलियों को एक दूसरे से जितना संभव हो उतना जुड़ा हुआ है)। गणितीय रूप से, यह इस तरह दिखता है:




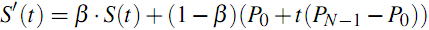
S (t) स्पेल पॉइंट हैं, S '(t) एक परिणामी वक्र है, जिसे स्क्रीन पर किनारे के रूप में खींचा जाता है।
खैर, यहाँ यह सब गणित का परिणाम क्या है:



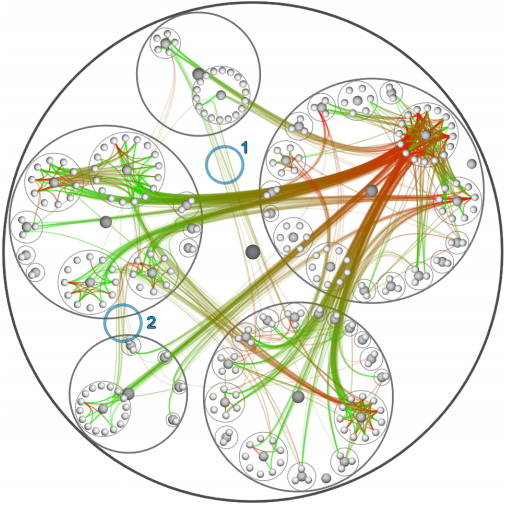
यहाँ Here = 0.85। अब कार्यक्रम की वास्तुकला बहुत स्पष्ट है। किनारों के अलग-अलग बंडल दिखाई देते हैं, पैकेज के बीच निर्भरताएं दिखाई देती हैं।
एक ही ग्राफ, केवल वास्तुकला के दृश्य की रेडियल विधि का उपयोग किया जाता है (विधि को लागू किए बिना, यह 0 0 0 के बराबर है:



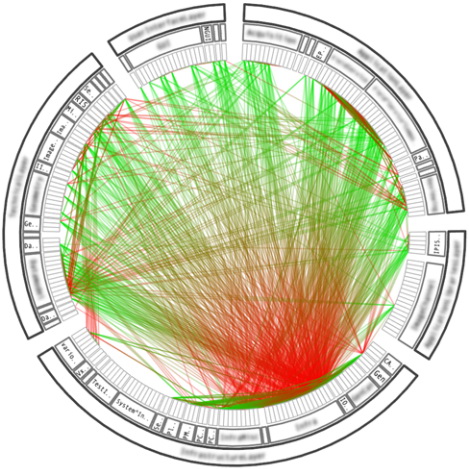
विधि का उपयोग करना (0. = 0.85):



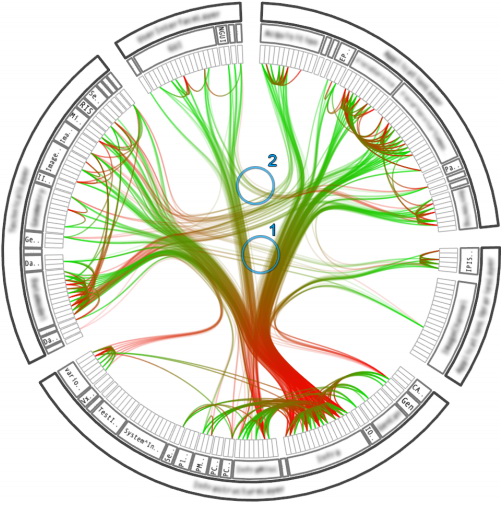
जैसा कि आप देख सकते हैं, किनारों को जोड़ने की विधि को ड्राइंग पेड़ों के विभिन्न तरीकों के साथ जोड़ा जा सकता है: यह इसका बहुत बड़ा लाभ है।

अन्य उदाहरण

प्रकाशनों का हवाला देते हैं। ग्रीन सर्कल 2008 के प्रकाशन हैं जो पिछले वर्षों (2007, 2006, आदि) से प्रकाशनों का हवाला देते हैं। केवल 2008 के प्रकाशनों के लिंक नोट किए गए हैं। विधि लागू किए बिना, यह इस तरह दिखता है:


विधि का उपयोग करना (0.99 = 0.99):

टिप्पणी

1. इससे बचने के लिए:



अल्फा चैनल का उपयोग कर सकते हैं:



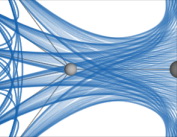
2. यदि आप नियंत्रण बहुभुज (कम से कम सामान्य पूर्वज, जुड़े हुए कोने के बीच कम से कम सामान्य पूर्वज) से एलसीए शीर्ष को हटाते हैं, तो ग्राफ बहुत बेहतर दिखेगा। अंतर पर एक नज़र डालें:



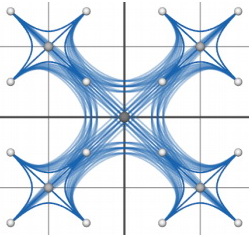
दूसरे मामले में, एलसीए शीर्ष को वर्टेक्स सेट से बाहर रखा गया है, और ग्राफ बहुत अधिक सुंदर दिखता है।

सी # कार्यान्वयन

नीचे विस्तार वर्ग System.rawing.Graphics का कार्यान्वयन है, जो एक सेट के माध्यम से क्यूबिक बी-स्पलाइन खींच सकता है।

using System;
using System.Text;
using System.Drawing;

static class GraphicsExtension
{
private static void DrawCubicCurve( this Graphics graphics, Pen pen, float beta, float step, PointF start, PointF end, float a3, float a2, float a1, float a0, float b3, float b2, float b1, float b0)
{
float xPrev, yPrev;
float xNext, yNext;
bool stop = false ;

xPrev = beta * a0 + (1 - beta) * start.X;
yPrev = beta * b0 + (1 - beta) * start.Y;

for ( float t = step; ; t += step)
{
if (stop)
break ;

if (t >= 1)
{
stop = true ;
t = 1;
}

xNext = beta * (a3 * t * t * t + a2 * t * t + a1 * t + a0) + (1 - beta) * (start.X + (end.X - start.X) * t);
yNext = beta * (b3 * t * t * t + b2 * t * t + b1 * t + b0) + (1 - beta) * (start.Y + (end.Y - start.Y) * t);

graphics.DrawLine(pen, xPrev, yPrev, xNext, yNext);

xPrev = xNext;
yPrev = yNext;
}
}

/// <summary>
/// Draws a B-spline curve through a specified array of Point structures.
/// </summary>
/// <param name="pen">Pen for line drawing.</param>
/// <param name="points">Array of control points that define the spline.</param>
/// <param name="beta">Bundling strength, 0 <= beta <= 1.</param>
/// <param name="step">Step of drawing curve, defines the quality of drawing, 0 < step <= 1</param>
internal static void DrawBSpline( this Graphics graphics, Pen pen, PointF[] points, float beta, float step)
{
if (points == null )
throw new ArgumentNullException( "The point array must not be null." );

if (beta < 0 || beta > 1)
throw new ArgumentException( "The bundling strength must be >= 0 and <= 1." );

if (step <= 0 || step > 1)
throw new ArgumentException( "The step must be > 0 and <= 1." );

if (points.Length <= 1)
return ;

if (points.Length == 2)
{
graphics.DrawLine(pen, points[0], points[1]);
return ;
}

float a3, a2, a1, a0, b3, b2, b1, b0;
float deltaX = (points[points.Length - 1].X - points[0].X) / (points.Length - 1);
float deltaY = (points[points.Length - 1].Y - points[0].Y) / (points.Length - 1);
PointF start, end;

{
a0 = points[0].X;
b0 = points[0].Y;

a1 = points[1].X - points[0].X;
b1 = points[1].Y - points[0].Y;

a2 = 0;
b2 = 0;

a3 = (points[0].X - 2 * points[1].X + points[2].X) / 6;
b3 = (points[0].Y - 2 * points[1].Y + points[2].Y) / 6;

start = points[0];
end = new PointF
(
points[0].X + deltaX,
points[0].Y + deltaY
);

graphics.DrawCubicCurve(pen, beta, step, start, end, a3, a2, a1, a0, b3, b2, b1, b0);
}

for ( int i = 1; i < points.Length - 2; i++)
{
a0 = (points[i - 1].X + 4 * points[i].X + points[i + 1].X) / 6;
b0 = (points[i - 1].Y + 4 * points[i].Y + points[i + 1].Y) / 6;

a1 = (points[i + 1].X - points[i - 1].X) / 2;
b1 = (points[i + 1].Y - points[i - 1].Y) / 2;

a2 = (points[i - 1].X - 2 * points[i].X + points[i + 1].X) / 2;
b2 = (points[i - 1].Y - 2 * points[i].Y + points[i + 1].Y) / 2;

a3 = (-points[i - 1].X + 3 * points[i].X - 3 * points[i + 1].X + points[i + 2].X) / 6;
b3 = (-points[i - 1].Y + 3 * points[i].Y - 3 * points[i + 1].Y + points[i + 2].Y) / 6;

start = new PointF
(
points[0].X + deltaX * i,
points[0].Y + deltaY * i
);

end = new PointF
(
points[0].X + deltaX * (i + 1),
points[0].Y + deltaY * (i + 1)
);

graphics.DrawCubicCurve(pen, beta, step, start, end, a3, a2, a1, a0, b3, b2, b1, b0);
}

{
a0 = points[points.Length - 1].X;
b0 = points[points.Length - 1].Y;

a1 = points[points.Length - 2].X - points[points.Length - 1].X;
b1 = points[points.Length - 2].Y - points[points.Length - 1].Y;

a2 = 0;
b2 = 0;

a3 = (points[points.Length - 1].X - 2 * points[points.Length - 2].X + points[points.Length - 3].X) / 6;
b3 = (points[points.Length - 1].Y - 2 * points[points.Length - 2].Y + points[points.Length - 3].Y) / 6;

start = points[points.Length - 1];

end = new PointF
(
points[0].X + deltaX * (points.Length - 2),
points[0].Y + deltaY * (points.Length - 2)
);

graphics.DrawCubicCurve(pen, beta, step, start, end, a3, a2, a1, a0, b3, b2, b1, b0);
}
}
}

* This source code was highlighted with Source Code Highlighter .

साहित्य

किनारों को बांधने की वर्णित विधि और लगभग सभी चित्रों को लेख से लिया गया है "श्रेणीबद्ध एज बंडल्स:
पदानुक्रमित डेटा में आसन्न संबंधों का दृश्य। " डैनी होल्टन द्वारा पोस्ट किया गया