हेबर के सभी पाठकों को नमस्कार! इस लेख को लिखने का निश्चय करने के बाद, मैंने हेबे को रेखांकन पर बहुत सारी सामग्री और विशेष रूप से
सामयिक छँटाई पर पाया । उदाहरण के लिए, सैद्धांतिक भाग का वर्णन
यहां कुछ विस्तार से किया गया है और बुनियादी एल्गोरिदम के उदाहरण दिए गए हैं। इसलिए, मैं खुद को नहीं दोहराऊंगा, लेकिन
टोपोलॉजिकल सॉर्टिंग के आवेदन के व्यावहारिक क्षेत्र के बारे में बात करूंगा, या इसके बजाय, मैं
DevExpress उत्पादों को विकसित करते समय इस पद्धति के साथ अपने व्यक्तिगत अनुभव को साझा करना चाहता हूं। लेख से, इस एल्गोरिथ्म के उपयोग को प्रेरित करने वाले उद्देश्य और कारण स्पष्ट हो जाएंगे। अंत में मैं आश्रित वस्तुओं को छांटने के लिए एल्गोरिथम का अपना संस्करण दूंगा।
DevExpress में छँटाई एल्गोरिथ्म का दायरा
पिछले लेख में, हमने
XtraScheduler अनुसूचक और इसके प्रिंट एक्सटेंशन के बारे में बात की थी। इसमें एक रिपोर्ट डिजाइनर शामिल है जो दृश्य तत्वों के साथ काम करता है। जब एक डिजाइनर में मुद्रित रूप की उपस्थिति को डिजाइन करते हैं, तो "मास्टर-अधीनस्थ" के सिद्धांत पर रिपोर्ट के दृश्य तत्वों के बीच लिंक स्थापित करना आवश्यक है। इन निर्भरताओं को यह निर्धारित करना चाहिए कि तत्वों के बीच डेटा कैसे स्थानांतरित किया जाता है। आंतरिक कार्यान्वयन के लिए, इसका तात्पर्य इन वस्तुओं के लिए सही प्रिंट प्राथमिकता के गठन से है।
संक्षेप में तत्व वस्तुओं के एक निर्देशित ग्राफ का प्रतिनिधित्व करते हैं, क्योंकि इन नियंत्रणों के विकल्पों ने मुख्य वस्तु के लिंक को निर्धारित करके निर्भरता की दिशा को विशिष्ट रूप से निर्धारित किया।
टोपोलॉजिकल सॉर्टिंग एल्गोरिथ्म छपाई से पहले सही क्रम में निर्भर वस्तुओं का निर्माण करने के लिए सबसे उपयुक्त था, जो उनके बीच संबंधों का विश्लेषण करता है। इसके अलावा, निर्भर नियंत्रणों ने मुद्रण करते समय मुख्य नियंत्रणों के प्रतिपादन डेटा का उपयोग किया। इसलिए, एल्गोरिथ्म का उपयोग आंतरिक डेटा कैशिंग वस्तुओं को व्यवस्थित करने के लिए भी किया गया था, जिसमें डेटा और संबंधित सबलिस्ट के अनुसार मुख्य पुनरावृत्त वस्तु होती है।
हमने एल्गोरिथ्म को और कहां लागू किया?
थोड़ी देर बाद,
XtraRichEdit परियोजना में
, RTF और DOC स्वरूपों में दस्तावेज़ों के लिए शैलियों के आयात और निर्यात का विकास करते समय
, सही क्रम में निर्भरता वाली वस्तुओं को प्राप्त करना भी आवश्यक हो गया। वर्णित एल्गोरिथ्म को सामान्यीकृत किया गया था और इस मामले में सफलतापूर्वक लागू किया गया था।
एल्गोरिथ्म टी
चलो छँटाई एल्गोरिथ्म के हमारे कार्यान्वयन के लिए आगे बढ़ते हैं। यह डोनाल्ड नुथ (अध्याय 2.2.3 का खंड 1)
द्वारा पुस्तक
"प्रोग्रामिंग की कला" से वर्णित एल्गोरिथम-टी पर आधारित है। इसलिए, आप मूल में एल्गोरिथ्म के विवरण के बारे में पढ़ सकते हैं, यहां मैं केवल विचार की सामान्य समझ के लिए एल्गोरिथ्म का एक आरेख दूंगा।
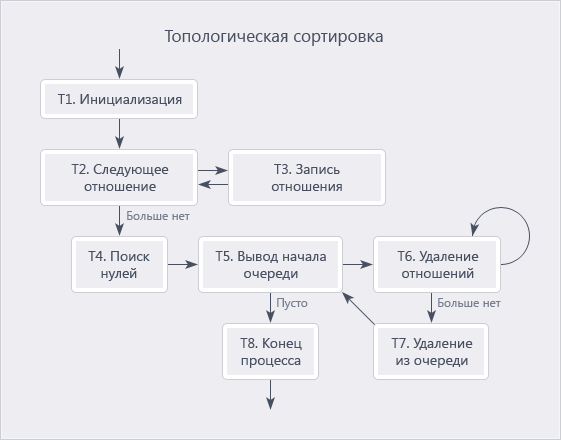
हमने इस एल्गोरिथम को क्यों चुना? बस मुझे लेखक को थोड़ा उद्धृत करना चाहिए।
"टी एल्गोरिथ्म का एक विश्लेषण किरचॉफ के नियम का उपयोग करके किया जा सकता है। इस कानून का उपयोग करते हुए, निष्पादन समय का अनुमान फॉर्मूला c1 * m + c2 * n का उपयोग करके लगाया जा सकता है, जहां m में दर्ज संबंधों की संख्या है, n वस्तुओं की संख्या है, और c1 और c2 स्थिरांक हैं। इस समस्या को हल करने के लिए एक तेज एल्गोरिदम केवल कल्पना करना असंभव है! "
कार्यान्वित एल्गोरिथ्म
एल्गोरिथ्म वर्ग में
DevExpress.Data.dll असेंबली में स्थित है, जिसमें टोपोलॉजिकल सॉर्टिंग के साथ कई अन्य उपयोगी एल्गोरिदम शामिल हैं।
namespace DevExpress.Utils { public static class Algorithms { public static IList<T> TopologicalSort<T>(IList<T> sourceObjects, IComparer<T> comparer) { TopologicalSorter<T> sorter = new TopologicalSorter<T>(); return sorter.Sort(sourceObjects, comparer); } }
एल्गोरिथ्म का उपयोग करना बेहद सरल है। यह कक्षा के स्थिर तरीके को कॉल करने के लिए पर्याप्त है, इसे आवश्यक पैरामीटर पास कर रहा है। एक उदाहरण कॉल इस प्रकार है:
protected virtual IList<XRControl> SortControls(List<XRControl> sourceControls) { return Algorithms.TopologicalSort<XRControl>(sourceControls, new ReportViewControlComparer()); }
आप स्पष्ट रूप से सॉर्टर ऑब्जेक्ट का एक उदाहरण बनाकर स्थिर पद्धति को कॉल किए बिना कर सकते हैं।
सॉर्टर क्लास का स्रोत कोड जो एल्गोरिथम को लागू करता है, वह लेख के अंत में दिया जाएगा।
जैसा कि मापदंडों से देखा जा सकता है, वस्तुओं की सूची के अलावा, एक विशेष तुलनित्र वस्तु विधि को पारित किया जाता है। यदि यह निर्दिष्ट नहीं है, तो डिफ़ॉल्ट ऑब्जेक्ट का उपयोग किया जाएगा। व्यवहार में, तुलनित्र वस्तु को आम तौर पर परिभाषित किया जाता है, क्योंकि इसमें यह है कि तुलना तर्क निर्धारित किया जाता है, जो कि तुलना की गई वस्तुओं के गुणों पर आधारित हो सकता है। इसके अलावा, इस तरह की वस्तु कई विरासत प्रकारों के लिए एक साथ कई IComparer इंटरफेस को लागू कर सकती है।
इस तरह के एक वर्ग के एक उदाहरण के रूप में, हम हमारे ReportViewControlComparer देंगे, जिसका उपयोग
XtraScheduler.Reporting लाइब्रेरी में किया जाता है:
public class ReportViewControlComparer : IComparer<XRControl>, IComparer<ReportViewControlBase> { #region IComparer<XRControl> Members public int Compare(XRControl x, XRControl y) { return CompareCore(x as ReportRelatedControlBase, y as ReportViewControlBase); } #endregion #region IComparer<ReportViewControlBase> Members public int Compare(ReportViewControlBase x, ReportViewControlBase y) { return CompareCore(x as ReportRelatedControlBase, y); } #endregion int CompareCore(ReportRelatedControlBase slave, ReportViewControlBase master) { if (slave != null && master != null) { if (slave.LayoutOptionsHorizontal.MasterControl == master || slave.LayoutOptionsVertical.MasterControl == master) return 1; } return 0; } }
आवेदन उदाहरण
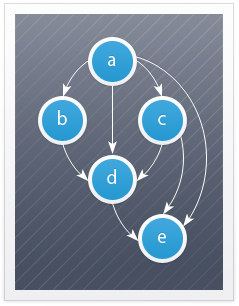
एल्गोरिथ्म के संचालन को प्रदर्शित करने के लिए, हम एक कंसोल एप्लिकेशन बनाएंगे। ग्राफ के एक उदाहरण के रूप में, हम 5 नोड्स का एक सरल ग्राफ लेते हैं (लेख की शुरुआत में आंकड़ा देखें)।
जी = ({ए, बी, सी, डी, ई}, {(ए, बी), (ए, सी), (ए, डी), (ए, ई), (बी, डी), (सी, डी) ), (सी, ई), (डी, ई)})ग्राफ का प्रतिनिधित्व करने के लिए, एक साधारण वर्ग का उपयोग किया जाएगा जो एक नोड को उससे जुड़े अन्य नोड्स की सूची के साथ परिभाषित करता है।
public class GraphNode { List<GraphNode> linkedNodes = new List<GraphNode>(); object id; public GraphNode(object id) { this.id = id; } public List<GraphNode> LinkedNodes { get { return linkedNodes; } } public object Id { get { return id; } } }
आवेदन के लिए कोड नीचे दिखाया गया है:
class Program { static void Main(string[] args) { DoDXTopologicalSort(); } private static void DoDXTopologicalSort() { GraphNode[] list = PrepareNodes(); Console.WriteLine("DX Topological Sorter"); Console.WriteLine(new string('-', 21)); Console.WriteLine("Nodes:"); GraphNode[] list = PrepareNodes(); PrintNodes(list); IComparer<GraphNode> comparer = new GraphNodeComparer(); IList<GraphNode> sortedNodes = DevExpress.Utils.Algorithms.TopologicalSort<GraphNode>(list, comparer); Console.WriteLine("Sorted nodes:"); PrintNodes(sortedNodes); Console.Read(); } static GraphNode[] PrepareNodes() { GraphNode nodeA = new GraphNode("A"); GraphNode nodeB = new GraphNode("B"); GraphNode nodeC = new GraphNode("C"); GraphNode nodeD = new GraphNode("D"); GraphNode nodeE = new GraphNode("E"); nodeA.LinkedNodes.AddRange(new GraphNode[] { nodeB, nodeC, nodeE }); nodeB.LinkedNodes.Add(nodeD); nodeC.LinkedNodes.AddRange(new GraphNode[] { nodeD, nodeE }); nodeD.LinkedNodes.Add(nodeE); return new GraphNode[] { nodeD, nodeA, nodeC, nodeE, nodeB }; } static void PrintNodes(IList<GraphNode> list) { for (int i = 0; i < list.Count; i++) { string s = string.Empty; if (i > 0) s = "->"; s += list[i].Id.ToString(); Console.Write(s); } Console.WriteLine("\r\n"); } }
डायरेक्ट ग्राफ रिलेशनशिप्स
प्रिपेंडेंस विधि में सेट किए गए हैं। इस मामले में, निर्भरताएँ मनमाने ढंग से बनाई जाती हैं।
नोड्स की तुलना करने के लिए, आपको GraphNodeComparer वर्ग की भी आवश्यकता होगी
public class GraphNodeComparer : IComparer<GraphNode> { public int Compare(GraphNode x, GraphNode y) { if (x.LinkedNodes.Contains(y)) return -1; if (y.LinkedNodes.Contains(x)) return 1; return 0; } }
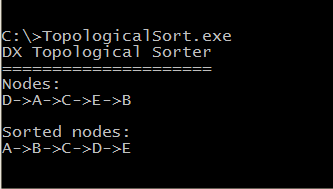
आवेदन शुरू करने के बाद, हमें नोड्स की एक क्रमबद्ध सूची मिलती है और कंसोल प्रदर्शित होगा
ए-> बी-> सी-> डी-> ई।कार्यक्रम का परिणाम नीचे दिए गए आंकड़े में दिखाया गया है:
सॉर्टर सोर्स कोड
जैसा कि मैंने ऊपर वादा किया था, मैं टोपोलॉजिकल सॉर्टिंग एल्गोरिदम के लिए कार्यान्वयन कोड देता हूं।
namespace DevExpress.Utils.Implementation {
#region TopologicalSorter
public class TopologicalSorter<T> {
#region Node
public class Node {
int refCount;
Node next;
public Node( int refCount, Node next) {
this .refCount = refCount;
this .next = next;
}
public int RefCount { get { return refCount; } }
public Node Next { get { return next; } }
}
#endregion
#region Fields
int [] qLink;
Node[] nodes;
IList<T> sourceObjects;
IComparer<T> comparer;
#endregion
#region Properties
protected internal Node[] Nodes { get { return nodes; } }
protected internal int [] QLink { get { return qLink; } }
protected IComparer<T> Comparer { get { return comparer; } }
protected internal IList<T> SourceObjects { get { return sourceObjects; } }
#endregion
protected IComparer<T> GetComparer() {
return Comparer != null ? Comparer : System.Collections. Generic .Comparer<T>.Default;
}
protected bool IsDependOn(T x, T y) {
return GetComparer().Compare(x, y) > 0;
}
public IList<T> Sort(IList<T> sourceObjects, IComparer<T> comparer) {
this .comparer = comparer;
return Sort(sourceObjects);
}
public IList<T> Sort(IList<T> sourceObjects) {
this .sourceObjects = sourceObjects;
int n = sourceObjects.Count;
if (n < 2)
return sourceObjects;
Initialize(n);
CalculateRelations(sourceObjects);
int r = FindNonRelatedNodeIndex();
IList<T> result = ProcessNodes(r);
return result.Count > 0 ? result : sourceObjects;
}
protected internal void Initialize( int n) {
int count = n + 1;
this .qLink = new int [count];
this .nodes = new Node[count];
}
protected internal void CalculateRelations(IList<T> sourceObjects) {
int n = sourceObjects.Count;
for ( int y = 0; y < n; y++) {
for ( int x = 0; x < n; x++) {
if (!IsDependOn(sourceObjects[y], sourceObjects[x]))
continue ;
int minIndex = x + 1;
int maxIndex = y + 1;
QLink[maxIndex]++;
Nodes[minIndex] = new Node(maxIndex, Nodes[minIndex]);
}
}
}
protected internal int FindNonRelatedNodeIndex() {
int r = 0;
int n = SourceObjects.Count;
for ( int i = 0; i <= n; i++) {
if (QLink[i] == 0) {
QLink[r] = i;
r = i;
}
}
return r;
}
protected virtual IList<T> ProcessNodes( int r) {
int n = sourceObjects.Count;
int k = n;
int f = QLink[0];
List <T> result = new List <T>(n);
while (f > 0) {
result.Add(sourceObjects[f - 1]);
k--;
Node node = Nodes[f];
while (node != null ) {
node = RemoveRelation(node, ref r);
}
f = QLink[f];
}
return result;
}
Node RemoveRelation(Node node, ref int r) {
int suc_p = node.RefCount;
QLink[suc_p]--;
if (QLink[suc_p] == 0) {
QLink[r] = suc_p;
r = suc_p;
}
return node.Next;
}
}
#endregion
* This source code was highlighted with Source Code Highlighter .
निष्कर्ष
यदि आवश्यक हो, तो एक-दूसरे पर निर्भर वस्तुओं के प्रसंस्करण के एक निश्चित क्रम में, उन्हें टोपोलॉजिकल सॉर्टिंग एल्गोरिदम का उपयोग करके पूर्व-आदेश दिया जा सकता है। नतीजतन, वस्तुओं का सही क्रम और उन पर कार्यों के निष्पादन का निर्माण होता है।
लेख में प्रस्तावित एल्गोरिथ्म निम्नलिखित लाभ प्रदान करता है:
- सामान्यीकरण (जेनेरिक) का उपयोग, अर्थात् इसका उपयोग विभिन्न प्रकार की वस्तुओं को सॉर्ट करने के लिए किया जा सकता है
- अपने स्वयं के तुलनाकर्ता वर्ग को परिभाषित करने की क्षमता, यानी यह आपको वस्तुओं की तुलना करने के लिए विभिन्न तर्क को लागू करने की अनुमति देता है।
- एल्गोरिथ्म की रैखिकता, एल्गोरिदम पुनरावर्ती नहीं है
स्रोत कोड के साथ एक उदाहरण
यहां उपलब्ध
है ।
मुझे उम्मीद है कि भविष्य की परियोजनाओं में यह सामग्री आपके लिए उपयोगी होगी।