एक द्विआधारी छवि में वस्तुओं की गिनती। भाग 1

अमूर्त

एक, दो, तीन, चार, पांच। हम छुपकर खेलेंगे। लेख बाइनरी छवि पर वस्तुओं को चिह्नित करने (या गिनने) के लिए एल्गोरिथ्म के बारे में बताता है और कैसे, एक अतिरिक्त पास के बिना, इन वस्तुओं की ज्यामितीय विशेषताओं की गणना की जाती है (अभी तक अप्रकाशित भाग 2 में)। इस प्रकार के एल्गोरिदम अक्सर बाइनरी तैयारी पर पैटर्न मान्यता में उपयोग किए जाते हैं और उनकी कम्प्यूटेशनल दक्षता दिखाते हैं।
लेख के अंत में, पाठकों को एक दिलचस्प समस्या पेश की जाती है, जिसका एक सक्षम समाधान मौजूद है और यह आवश्यक है, एल्गोरिथम के व्यावहारिक कार्यान्वयन में। स्रोत कोड दिया गया है, लेकिन मेरे पिछले पोस्टों के विपरीत, इसे माटलैब भाषा में नहीं बल्कि बिल्कुल मुफ्त में, कम शक्तिशाली SciLab वातावरण में निष्पादित किया गया था।

परिचय

वास्तविक समय में उपयोग के लिए डिज़ाइन किए गए व्यावहारिक अनुप्रयोगों में, पैटर्न की पहचान अक्सर निम्नलिखित अनुक्रम के रूप में की जाती है:
छवि अधिग्रहण (1) -> अनुकूली द्वैरीकरण (2) -> आकारिकी संचालन की श्रृंखला (3) -> अंकन वस्तुओं (4) -> वस्तुओं की सुविधाओं के स्थान को भरना (5)।

चित्र 1 - छवि पर एक सरलीकृत पैटर्न मान्यता पैटर्न। योजना सुविधा स्थान को विभाजित करने और निर्णय लेने के चरणों को समाप्त करती है।

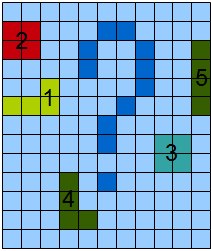
चित्र 2 में बैनरीकरण के बाद छवि के टुकड़े और रूपात्मक संचालन (छवि 2 ए) और वास्तविक मार्कअप परिणाम (छवि। 2 बी) की एक श्रृंखला को दिखाया गया है।

चित्रा 2 - ए) एक बिनाराइज्ड छवि है, बी) चिह्नित वस्तुओं के साथ एक छवि है।

लेख में हम न केवल वस्तुओं को चिह्नित करेंगे, बल्कि क्षेत्र और परिधि जैसी ज्यामितीय विशेषताओं की भी गणना करेंगे। उनके रिश्ते वस्तु की कॉम्पैक्टनेस और मालिनोवस्की फॉर्म फैक्टर का वर्णन कर सकते हैं, और अधिक जटिल ज्यामितीय विशेषताओं, बढ़ाव और समोच्च सुविधाओं के संयोजन में।

वैज्ञानिक रूप से, हम जो प्राप्त करना चाहते हैं उसे संबंधित क्षेत्रों का आवंटन कहा जाता है। इस समस्या के कई समाधान हैं - टेम्पलेट्स पर आधारित [1], कुछ पुनरावर्ती कार्यान्वयन (उदाहरण के लिए, [2] से सूची 1, आदि)।

शून्य लेबलिंग (BIT * img [], int * लेबल [])
{
int L = 1;
के लिए ( int y = 0; y <H; ++ y)
के लिए ( इंट x = 0; x <W; ++ x)
भरें (img, लेबल, x, y, L ++);
}
शून्य भरण (BIT * img [], int * लेबल [], int x, int y, int L)
{
अगर ((लेबल [x] [y] == ०) और (img [x] [y] == १))
{
लेबल [x] [y] = L;
अगर (x> 0)
भरें (img, लेबल, x - 1, y, L);
अगर (x <W - 1)
भरें (img, लेबल, x + 1, y, L);
अगर (y> 0)
भरें (img, लेबल, x, y - 1, L);
अगर (y <H - 1)
भरें (img, लेबल, x, y + 1, L);
}
}

* इस सोर्स कोड को सोर्स कोड हाइलाइटर के साथ हाइलाइट किया गया था।
लिस्टिंग 1 - जुड़े डोमेन के लिए मार्कअप एल्गोरिदम का एक पुनरावर्ती कार्यान्वयन।

यह सब हमें शोभा नहीं देता।
यदि इस क्षेत्र के प्रत्येक पिक्सेल के लिए उसी क्षेत्र से कोई पड़ोसी मौजूद है, तो एक पिक्सेल डोमेन को कनेक्ट किया जाएगा। कनेक्टिविटी के प्रकारों के बारे में मैंने इस विषय में एक चित्र दिया है (चित्र 1,2)। हमारा एल्गोरिथ्म चार जुड़ा हुआ होगा, हालांकि इसे बहुत अधिक मानसिक प्रयास के बिना आठ जुड़े वेरिएंट के लिए फिर से तैयार किया जा सकता है।

एक-पास, गैर-पुनरावर्ती मार्कअप एल्गोरिदम

इस एल्गोरिथ्म का विचार एक कोने के उपयोग पर आधारित है - एक एबीसी मास्क, जिसे चित्र 3 में दिखाया गया है।
चित्रा 3 - एबीसी मुखौटा और अनुक्रमिक छवि स्कैनिंग की दिशा।

इस मुखौटे की छवि के माध्यम से मार्ग बाएं से दाएं और ऊपर से नीचे तक किया जाता है। यह माना जाता है कि छवि सीमा से परे कोई वस्तु नहीं है, इसलिए, यदि बी या सी वहां गिरते हैं, तो स्कैनिंग के दौरान अतिरिक्त सत्यापन की आवश्यकता होती है। चित्र 4 में छवि में 5 संभावित मुखौटा स्थिति दिखाई गई है।
उन पर विचार करें।

चित्र 4 - एबीसी मास्क के पांच संभावित स्थान

1. नंबर 0 पर स्थिति, जब मास्क के सभी तीन घटक चिह्नित नहीं होते हैं - इस मामले में, हम सिर्फ पिक्सेल को छोड़ देते हैं।
2. नंबर 1 पर स्थिति, जब केवल ए तत्व चिह्नित किया जाता है - इस मामले में हम एक नई वस्तु बनाने की बात कर रहे हैं - एक नया नंबर।
3. स्थिति संख्या 2, जब कोई तत्व तत्व बी चिह्नित होता है - इस मामले में, हम वर्तमान पिक्सेल ए को बी में स्थित एक लेबल के साथ चिह्नित करते हैं।
4. नंबर 3 पर स्थिति, जब तत्व को तत्व सी चिह्नित किया जाता है - इस मामले में, हम वर्तमान पिक्सेल ए को सी में स्थित एक लेबल के साथ चिह्नित करते हैं।
5. नंबर 4 पर स्थिति, तो हम कहते हैं कि लेबल (ऑब्जेक्ट नंबर) B और C जुड़े हुए हैं - अर्थात, समतुल्य और पिक्सेल A को B या C के रूप में लेबल किया जा सकता है। कुछ कार्यान्वयन में, इस तरह के लेबल का एक तुल्यता ग्राफ बनाया जाता है, उसके बाद विश्लेषण, लेकिन मेरी राय में यह आवश्यक नहीं है। हम ऐसा करेंगे - यदि B, C के बराबर नहीं है, तो हम लेबल B में C के रूप में चिह्नित सभी पहले से संसाधित पिक्सल को फिर से सेट करते हैं, लेकिन इसके बारे में बहुत अंत में।

कार्यान्वयन के करीब।
सबसे पहले, चित्रा 2 में दिखाए गए लोगों के समान परीक्षण डेटा बनाएं, अर्थात्, शून्य और लोगों से मिलकर छवि मैट्रिक्स।

छवि = [0 0 0 0 0 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 1 0 0;
0 1 1 1 1 0 0 1 1 1 1;
0 1 1 1 1 0 0 0 0 0 0;
0 1 1 1 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 1 1 0 0;
0 0 0 0 0 0 1 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 1 1;
0 1 1 1 0 1 1 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 0 0]
Matplot (छवि * 255) // आइए चित्र में हमारे मैट्रिक्स को देखें
[एम, एन] = आकार (छवि); // मैट्रिक्स के क्षैतिज और ऊर्ध्वाधर आयामों का पता लगाएं
किमी = 0; kn = 0; // वे अभी भी हमारे लिए उपयोगी होंगे
cur = 1; / / गिनती वस्तुओं के लिए चर

* इस सोर्स कोड को सोर्स कोड हाइलाइटर के साथ हाइलाइट किया गया था।
लिस्टिंग 2 - स्रोत डेटा को इनिशियलाइज़ करना।

और फिर सरल और स्पष्ट चेक की एक श्रृंखला का प्रदर्शन करके छवि के माध्यम से जाओ। एबीसी मास्क, जिसे हम चित्र के माध्यम से गुजरते हैं, चित्र 3 में चित्रित किया गया है। इस मुखौटा द्वारा जांचे जाने वाले संभावित संयोजनों को चित्र 4 में दिखाया गया है।

// छवि पिक्सल का चक्र
i = 1: 1: m के लिए
j = 1: 1: n के लिए
kn = j - 1;
अगर kn <= 0 हो तो
kn = 1;
बी 0 है;
अन्यथा
बी = छवि (मैं, घुटने); // लेख में चित्र 3 देखें
अंत
किमी = मैं - 1;
यदि किमी <= 0 तो
किमी = 1;
सी 0 है;
अन्यथा
सी = छवि (किमी, जे); // लेख में चित्र 3 देखें
अंत
ए = छवि (आई, जे); // लेख में चित्र 3 देखें
यदि A == 0 तो // यदि वर्तमान पिक्सेल खाली है, तो कुछ भी न करें
अन्य बी == 0 & C == 0 तब // यदि हमारा पिक्सेल खाली है और वह खाली नहीं है - तो यह एक नई वस्तु के बारे में सोचने का एक अवसर है।
cur = cur + 1;
छवि (i, j) = वक्र;
और फिर बी ~ = ० और सी == ०
छवि (i, j) = B;
उसके बाद B == 0 और C ~ = 0 तब
छवि (i, j) = C;
और फिर बी ~ = 0 और सी ~ = ०
अगर B == C तब
छवि (i, j) = B;
अन्यथा
छवि (i, j) = B;
छवि (छवि == सी) = बी;
अंत
अंत
अंत
अंत

* इस सोर्स कोड को सोर्स कोड हाइलाइटर के साथ हाइलाइट किया गया था।
लिस्टिंग 3 - छवि पिक्सेल की क्रमिक स्कैनिंग और जुड़े क्षेत्रों को चिह्नित करना।

इस स्क्रिप्ट का परिणाम एक लेबल मैट्रिक्स होगा:

चित्र 5 - लिस्टिंग 2 और 3 के परिणाम - वस्तुओं को अद्वितीय संख्याएं दी गई हैं।

नुकसान यह है कि संख्या अनुक्रमिक नहीं हैं, लेकिन बड़े और यह बिल्कुल आवश्यक नहीं है, लेकिन यह एल्गोरिथ्म के अतिरिक्त संशोधनों द्वारा तय किया गया है।

लेख के पहले भाग के निष्कर्ष में, लेबल रीकॉम्बिंग को पूरी तरह से छोड़ दिया जा सकता है यदि किसी विशेष संरचना के लिए संकेत मैट्रिक्स का उपयोग बुद्धिमानी से किया जाता है। इस पर, मैं पाठक को प्रतिबिंबित करने का प्रस्ताव करता हूं। SciLab में पॉइंटर्स के साथ संस्करण को लागू करना संभव नहीं होगा, हालांकि, लेख के अंतिम तीसरे भाग में मैं छद्मकोड का उपयोग करके ऐसा करूंगा।

दूसरे भाग में क्या होगा - यह वस्तुओं के आकार, कॉम्पैक्टनेस और मालिनोवस्की कारक के अनुभवजन्य कारकों के बारे में बात करेगा। हम एक अद्वितीय चित्रण देखेंगे, जिसे मैं वर्तमान में काम कर रहा हूं, जिस पर किसी वस्तु के आकार में एक सहज परिवर्तन उसके कारक रूप में वृद्धि या कमी से परिलक्षित होता है।

आपकी प्रतिक्रिया का इंतजार कर रहे सभी लोगों को धन्यवाद।

संदर्भ और संदर्भ

[१] इमेज लिंक में एलगोरिदम / काउंटिंग ऑब्जेक्ट (जाहिरा तौर पर यह लेख एक बार हैबे पर था, लेकिन ऐसा नहीं हो सकता था)
[२] व्याख्यान: पीपीटी फ़ाइल में छवि लिंक में निहित जानकारी का विश्लेषण