
डिस्टेंस मैप एक ऐसी वस्तु है जो आपको दिए गए बिंदु से एक विशिष्ट सतह तक जल्दी से दूरी प्राप्त करने की अनुमति देती है। आमतौर पर एक निश्चित पिच के साथ नोड्स के लिए दूरी मूल्यों का एक मैट्रिक्स। यह अक्सर एक खिलाड़ी या वस्तु में "प्राप्त करने" और वस्तुओं के संयोजन में अनुकूलन कार्यों को निर्धारित करने के लिए खेलों में उपयोग किया जाता है: वस्तुओं को यथासंभव एक दूसरे के करीब स्थिति, लेकिन ताकि वे ओवरलैप न हों। पहले मामले में, दूरी के नक्शे की गुणवत्ता (यानी, नोड्स में मूल्यों की सटीकता) एक बड़ी भूमिका नहीं निभाती है। दूसरे में, जीवन इस पर निर्भर कर सकता है (न्यूरोसर्जरी से संबंधित कई अनुप्रयोगों में)। इस लेख में मैं आपको बताऊंगा कि उचित समय में दूरी के नक्शे की सही गणना कैसे करें।
मुख्य वस्तुएं
मान लीजिए कि हमारे पास कुछ सतह S है जो स्वरों के एक समूह द्वारा परिभाषित की गई है। स्वर निर्देशांक को एक नियमित ग्रिड पर गिना जाएगा (यानी एक्स, वाई और जेड के साथ कदम समान हैं)।
सभी वेक्सल्स के लिए दूरी के नक्शे M [X, Y, Z] की गणना करना आवश्यक है जो सतह से युक्त क्यूब में झूठ बोलते हैं; M [x, y, z] = d ((x, y, z), S) = मिनट (d (x, y, z), (S
n x, S
n y, S
n z)) = sqrt (न्यूनतम (xS
n x)
2 + (yS
n y)
2 + (zS
n z)
2 ))। अंतिम समानता केवल एक नियमित ग्रिड के लिए सही है, बाकी स्पष्ट होना चाहिए।
डेटा कहां से आता है
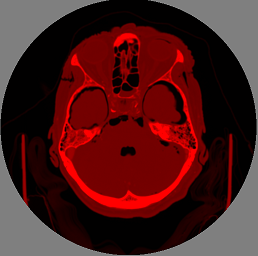
हमारे कार्य के लिए, डेटा एक
एमआरआई डिवाइस से आता है। मुझे याद दिलाएं कि हम 3 डी छवियों के साथ काम करते हैं, इसलिए पूरी 3 डी छवि जेड में विभिन्न स्लाइस के लिए फ्लैट छवियों का एक सेट है, जो मैं निश्चित रूप से यहां कल्पना नहीं कर सकता हूं; वे X और Y रिज़ॉल्यूशन से थोड़े छोटे हैं। विशिष्ट टोमोग्राफी का आकार लगभग 625x625x592 स्वर है।

बल्कि मुश्किल परिवर्तनों के परिणामस्वरूप, सिर की सतह की सीमा को उजागर किया जाता है। इन परिवर्तनों का बहुत सार विभिन्न प्रकार के फिल्टर के लिए नीचे आता है जो "शोर" और फ़ंक्शन को हटाते हैं जो ढाल द्वारा सीमा को निर्धारित करता है। यहां कुछ भी नया नहीं है,
विशेष रूप से "इमेज प्रोसेसिंग" के विषय में ऐसी चीजों का वर्णन किया गया था। सीमा ही वह लक्ष्य सेट है जिससे हम दूरियों की गणना करेंगे और एक मानचित्र बनाएंगे।
प्रत्यक्ष खोज
सबसे पहले, आइए अनुमान करें कि "परिभाषा के अनुसार" मानों के साथ दूरी का नक्शा क्यों न भरें - सीमा बिंदुओं की न्यूनतम दूरी। कुल नक्शा अंक: X * Y * Z, ऑर्डर अधिकतम का सतह अंक (X, Y, Z)
2 । स्रोत डेटा के आकारों को याद करें और 592 * 625
4 अंकगणितीय-तार्किक संचालन के क्रम के बारे में कुछ प्राप्त करें। कैलकुलेटर आपको बताएगा कि यह 90,000 बिलियन से अधिक है। इसे हल्के ढंग से रखने के लिए, बहुत अधिक, हम अब प्रत्यक्ष खोज के लिए स्थगित कर देंगे।
गतिशील प्रोग्रामिंग
यह इस तथ्य के उपयोग को बताता है कि डेटा को तीन-आयामी सरणी में दर्शाया गया है; आप किसी भी तरह अपने पड़ोसियों का उपयोग करके प्रत्येक बिंदु पर मूल्य की गणना कर सकते हैं, और निश्चित रूप से हम ऐसा करने वाले पहले नहीं हैं। तथ्य यह है कि आकार में 592 * 625 * 625 * 625 आकार (फ्लोट) की संरचना रखते हुए, जो कि लगभग 1 गीगाबाइट है, कुछ हद तक संसाधन-गहन है, कुछ हद तक प्रतिकारक है। ठीक है, ठीक है, यह भूल जाते हैं कि टोमोग्राफी को दोहरे संकल्प (एक और 8 गुना अधिक) के साथ शूट किया जा सकता है - 640Kbytes लंबे समय तक गायब हैं।
भराव (शहर-ब्लॉक) भरने की सबसे तुच्छ विधि,
भूलभुलैया को दरकिनार करने के लिए
एल्गोरिदम के समान, सेकंड के एक मामले में पूरी होती है, लेकिन तीन-आयामी ग्रिड पर अधिकतम त्रुटि 50 चरणों की अधिकतम गणना की गई दूरी के लिए 42 ग्रिड चरण हो सकती है। कितना बुरा है? पूर्ण विफलता।
वर्ग (
केंद्रीय बिंदु ) से एकमात्र एल्गोरिथ्म लगभग संतोषजनक सटीकता (0.7 ग्रिड से अधिक नहीं की त्रुटि) देता है, लेकिन मिनट काम करता है।
हमने शतरंज की दूरी को लागू करके एक समझौता खोजने की कोशिश की (विवरण केंद्रीय बिंदु के समान लेख में है), लेकिन अंतिम सटीकता की व्यवस्था नहीं की जा सकी, और इसके संचालन का समय दसियों सेकंड था।

यह चित्र पूर्ण-आकार की एक कड़ी है, लेकिन यहां तक कि पूर्वावलोकन "अजीब" व्यवहार को सतह के बिंदुओं से काफी दूर दिखाता है, और खासकर अगर आपको आंतरिक वस्तुओं को भी गिनने की आवश्यकता है। बाईं ओर शतरंज की बिसात है, और दायीं ओर वह है जो प्रत्यक्ष गणना द्वारा प्राप्त किया गया था। और मैं आपको फिर से याद दिलाऊंगा, जो केवल चित्रों को देखते हैं - हम 3 डी छवियों के बारे में बात कर रहे हैं, इसलिए अंदर अजीब "पंचर" समझ में आते हैं - वे अगले या पिछले जेड स्लाइड पर सतह के निकटता के कारण होते हैं। सामान्य तौर पर, एक विफलता।
फिर से प्रत्यक्ष खोज
हां, तस्वीर में CUDA शब्द इशारा कर रहा है। शायद 90,000 बिलियन - इतना नहीं, या शायद यह संख्या किसी तरह कम हो सकती है, सटीकता की हानि के बिना। किसी भी मामले में, मध्य-अंत वीडियो कार्ड एक ही वर्ग के प्रोसेसर की तुलना में 80-120 गुना तेजी से आदिम कंप्यूटिंग संचालन को संभालता है। आइए कोशिश करते हैं।
हां, और प्रत्यक्ष गणना का एक महत्वपूर्ण लाभ है - स्मृति में पूरी दूरी के नक्शे को रखने की आवश्यकता नहीं है, और परिणामस्वरूप - रैखिक स्थिरता।
बस्ट रिडक्शन
थीसिस: यह सीमा के प्रत्येक बिंदु के लिए दूरी की जांच करने के लिए प्रत्येक बिंदु के लिए कोई मतलब नहीं है। वास्तव में, दूरी के नक्शे को केवल सीमा के करीब निकटता में अच्छी सटीकता सुनिश्चित करनी चाहिए, बल्कि दूर के बिंदुओं को पूरी तरह से छोड़ा जा सकता है, और मध्यवर्ती बिंदुओं को अनुमानित दूरी के साथ चिह्नित किया जाना चाहिए।
शुद्धता मानदंड सीमा के पास पूर्ण सटीकता है (10 (GUARANTEED_DIST) ग्रिड चरणों की दूरी पर), 36 की दूरी पर अच्छी सटीकता (TARGET_MAX_DIST) चरणों, और दृश्यता (कलाकृतियों के बिना - क्यों सर्जनों को भ्रमित करें)। संख्या 10 और 36 को सीधे हमारे कार्य से लिया जाता है (हम आम तौर पर मिलीमीटर और मिलीमीटर ग्रिड में ये मान रखते हैं)।
घन सूचकांक
प्रत्येक बिंदु के लिए, मैं यह निर्धारित करना चाहूंगा कि इसके मूल्य की गणना कितनी सही है। जाहिर है, ऐसी संरचना का आकार मूल छवि के आकार के साथ मेल खाएगा, और यह बहुत कुछ है, और लंबे समय तक माना जाएगा।
हम "क्यूब्स" में अंकों को मिला देंगे। घन आकार 32 (CUBE_SIZE) होने दें, फिर सूचकांक में 20 x 20 x 19 आयाम होंगे।
हम क्यूब को "सबसे अच्छा" बिंदु के प्रकार के अनुसार चिह्नित करते हैं। यदि कम से कम एक बिंदु के लिए सटीक गणना की आवश्यकता होती है, तो हम पूरे घन को सुनिश्चित करने के लिए विचार करते हैं। सबसे बुरे मामले में, हम बिल्कुल भी नहीं सोचते हैं।
कैसे जल्दी से क्यूब्स लेबल करने के लिए? चलो सीमा बिंदुओं से शुरू करते हैं: उनमें से प्रत्येक को ऑफसेट करें GUARANTEED_DIST को सभी 27 दिशाओं (-1,0,1) x (-1,0,1) x (-1,0,1) में जोड़ें, हमें संबंधित घन का सूचकांक मिलता है। 32 (CUBE_SIZE) द्वारा विभाजित, और इसे "सटीक" के रूप में चिह्नित करें - आखिरकार, इसमें कम से कम एक बिंदु होता है जिसे सटीक गणना की आवश्यकता होती है। उद्देश्य: यह समझाने के लिए कि यह पर्याप्त क्यों है, और सटीक गणना के लिए अंक वाले सभी क्यूब्स को सही तरीके से चिह्नित किया जाएगा।
बस मामले में, यह निष्पादित करने वाला सुंदर तुच्छ कोड है:
for (size_t t = 0; t < borderLength; t++)
{
for ( int dz = -1; dz <= 1; dz++)
for ( int dy = -1; dy <= 1; dy++)
for ( int dx = -1; dx <= 1; dx++)
{
float x = border[t].X + ( float )dx * GUARANTEED_DIST;
float y = border[t].Y + ( float )dy * GUARANTEED_DIST;
float z = border[t].Z + ( float )dz * GUARANTEED_DIST;
if (x >= 0 && y >= 0 && z >= 0)
{
size_t px = round(x / CUBE_SIZE);
size_t py = round(y / CUBE_SIZE);
size_t pz = round(z / CUBE_SIZE);
size_t idx = px + dim_X * (py + skip_Y * pz);
if (idx < dim_X * dim_Y * dim_Z)
{
markedIdx[idx] = true ;
}
}
}
}
व्यावहारिक आंकड़ों के आधार पर, इस विचार ने "कुल" के खोज क्रम को 4-5 गुना कम करना संभव बना दिया। सभी समान, यह बहुत कुछ निकला, लेकिन क्यूब्स के साथ विचार अभी भी हमारे लिए उपयोगी है।
घन कंटेनर
वास्तव में, सीमा के सभी बिंदुओं से दूरी की गणना करने का कोई मतलब नहीं है, यह केवल निकटतम बिंदुओं के लिए गणना करने के लिए पर्याप्त है; और अब हम जानते हैं कि इस तरह की संरचना को कैसे व्यवस्थित किया जाए।
हम सीमा S के सभी स्वरों को क्यूब्स में बिखेर देंगे (हम अब से इंडेक्स क्यूब्स के बारे में भूल जाएंगे; हमने उन्हें बनाया था, उन्हें कैसे उपयोग करना है, यह समझ में आया और अब हम उनके साथ काम नहीं करते हैं)। प्रत्येक क्यूब में हम उन बॉर्डर पॉइंट्स को डालेंगे जो कि पहुंच योग्य (TARGET_MAX_DIST और उससे कम की दूरी पर स्थित हैं)। ऐसा करने के लिए, बस घन के केंद्र की गणना करें, और दूरी sqrt (3) / 2 * CUBE_SIZE (यह घन का विकर्ण है) + TARGET_MAX_DIST डाल दें। यदि बिंदु घन के शीर्ष से या किसी ओर से पहुंच योग्य है, तो यह उसके अंदर से पहुंच योग्य है।
मुझे लगता है कि यह कोड देने के लिए कोई मतलब नहीं है, यह पिछले एक के समान है। और विचार की शुद्धता भी स्पष्ट है, लेकिन एक आवश्यक बिंदु बना हुआ है: वास्तव में, हम सीमा के बिंदुओं को "गुणा" करते हैं, जिसकी संख्या एक उचित TARGET_MAX_DIST (क्यूब के आकार से कम) के साथ 27 गुना तक बढ़ सकती है और इससे भी अधिक अलग-अलग समय में।
अनुकूलन:
- पहला (मजबूर) - क्यूब का आकार इसलिए चुना गया है ताकि "गुणा" अंक की कुल संख्या उन पर मेमोरी की अधिकतम मात्रा से अधिक न हो (हमने 512 मेगाबाइट लिया)। आप घन आकार को जल्दी से चुन सकते हैं (थोड़ा गणित)।
- दूसरा (उचित) प्रत्येक क्यूब के लिए बिंदुओं के प्रारंभिक और अंतिम स्थान पर अनुक्रमित का उपयोग करना है, ये सूचकांक प्रतिच्छेद कर सकते हैं, और उनकी सक्षम गणना के कारण, आप स्मृति आकार में एक और 2 बार बचा सकते हैं।
मैं जानबूझकर दोनों बिंदुओं के लिए सटीक एल्गोरिदम नहीं दूंगा (यदि आप उन्हें बेहतर तरीके से लागू करते हैं और हमारे प्रतिस्पर्धी बन जाते हैं?)), विचारों से अधिक शब्द हैं।
सामान्य तौर पर, क्यूब्स X / CUBE_SIZE * Y / CUBE_SIZE * Z / CUBE_SIZE समय द्वारा खोज क्रम को कम करते हैं, लेकिन हमें याद रखना चाहिए कि क्यूब के आकार को कम करने के लिए बहुत अधिक मेमोरी की आवश्यकता होगी, और हमारी छवियों के लिए सीमा मूल्य 24-32 के आसपास निकला।
इस प्रकार, यह कार्य लगभग 100-200 बिलियन के भौतिक संचालन में कम हो गया। सैद्धांतिक रूप से, यह दसियों सेकंड में एक ग्राफिक्स कार्ड पर कम्प्यूटेशनल है।
कूडा कर्नेल
यह इतना सरल और सुंदर निकला कि मैं इसे दिखाने के लिए बहुत आलसी नहीं हूं:
__global__ void minimumDistanceCUDA( /*out*/ float *result,
/*in*/ float *work_points,
/*in*/ int *work_indexes,
/*in*/ float *new_border)
{
__shared__ float sMins[MAX_THREADS]; // max threads count
for ( int i = blockIdx.x; i < BLOCK_SIZE_DIST; i += gridDim.x)
{
sMins[threadIdx.x] = TARGET_MAX_DIST*TARGET_MAX_DIST;
int startIdx = work_indexes[2*i];
int endIdx = work_indexes[2*i+1];
float x = work_points[3*i];
float y = work_points[3*i+1];
float z = work_points[3*i+2];
// main computational entry
for ( int j = startIdx + threadIdx.x; j < endIdx; j += blockDim.x)
{
float dist = (x - new_border[3*j] )*(x - new_border[3*j] )
+ (y - new_border[3*j+1])*(y - new_border[3*j+1])
+ (z - new_border[3*j+2])*(z - new_border[3*j+2]);
if (dist < sMins[threadIdx.x])
sMins[threadIdx.x] = dist;
}
__syncthreads();
if (threadIdx.x == 0)
{
float min = sMins[0];
for ( int j = 1; j < blockDim.x; j++)
{
if (sMins[j] < min)
min = sMins[j];
}
result[i] = sqrt(min);
}
__syncthreads();
}
}
हम बॉर्डर पॉइंट्स (वर्क_इन्डेक्स) की गणना के लिए गणना (वर्क_ पॉइंट्स), संबंधित प्रारंभ और अंत सूचक के लिए दूरी मानचित्र बिंदुओं के समन्वय ब्लॉक को लोड करते हैं और क्यूब्स (new_border) के साथ एल्गोरिदम द्वारा अनुकूलित सीमा। हम परिणामों को एकल सामग्री सटीकता में लेते हैं।
वास्तव में, कर्नेल कोड ही, जिसे समझना बहुत अच्छा है, यहां तक कि CUDA की पेचीदगियों के बिना भी। इसकी मुख्य विशेषता ग्रिडडीम.एक्स और थ्रेडआईएक्सएक्सएक्सएक्स चर का उपयोग है जो वीडियो कार्ड पर चल रहे थ्रेड्स के सेट से वर्तमान थ्रेड के सूचकांकों को दर्शाते हैं - हर कोई एक ही काम करता है, लेकिन विभिन्न बिंदुओं के साथ, और फिर परिणाम सिंक्रनाइज़ और सटीक रूप से दर्ज किए जाते हैं।
यह सीपीयू पर वर्क_ पॉइंट्स की गणना को सही ढंग से व्यवस्थित करने के लिए ही बना हुआ है (लेकिन यह इतना आसान है!) और कैलकुलेटर शुरू करें:
#define GRID 512 // calculation grid size
#define THREADS 96 // <= MAX_THREADS, optimal for this task
minimumDistanceCUDA<<<GRID, THREADS>>>(dist_result_cuda, work_points_cuda, work_indexes_cuda, new_border_cuda);
एक कोर डुओ E8400 और एक GTX460 ग्राफिक्स कार्ड पर, औसत टोमोग्राफी
एक मिनट के भीतर संसाधित की
जाती है और मेमोरी खपत 512MB तक सीमित होती है। सीपीयू और फ़ाइल संचालन पर प्रोसेसर समय का वितरण लगभग 20 प्रतिशत है, और शेष 80 वीडियो कार्ड पर चढ़ाव की गणना पर।
और यहां दूर के बिंदुओं के "मोटे तौर पर" के साथ गिना गया चित्र है:

किसी तरह, मुझे आशा है कि कुछ काम आता है। एक बड़ा अनुरोध, चित्रों को कॉपी न करें और मेरी अनुमति के बिना फिर से प्रकाशित न करें (मैं विधि का लेखक हूं, हालांकि इसे "विधि" कहना मुश्किल है)।
आपका दिन शुभ हो!