लॉगलॉग - अद्वितीय तत्वों की संख्या का पता लगाएं

नमस्कार, हेब्र! आप और मैं पहले ही ब्लूम और मिनहैश फिल्टर में लिप्त हो चुके हैं। आज हम एक और संभाव्य-यादृच्छिक-एल्गोरिथ्म के बारे में बात करेंगे जो आपको न्यूनतम मेमोरी ओवरहेड के साथ बड़ी मात्रा में अद्वितीय तत्वों की अनुमानित संख्या निर्धारित करने की अनुमति देता है।

शुरू करने के लिए, आइए हम अपने आप को कार्य निर्धारित करें: मान लें कि हमारे पास बड़ी मात्रा में शाब्दिक डेटा है - कहते हैं, कुख्यात शेक्सपियर के साहित्यिक कार्य का फल है, और हमें इस मात्रा में पाए गए विभिन्न शब्दों की संख्या की गणना करने की आवश्यकता है। एक विशिष्ट समाधान एक ट्रंकेटेड हैश तालिका के साथ एक काउंटर है, जहां कुंजी उनके साथ जुड़े मूल्यों के बिना शब्द होंगे।

जिस तरह से सभी के लिए अच्छा है, लेकिन इसके काम के लिए अपेक्षाकृत बड़ी मात्रा में स्मृति की आवश्यकता होती है, लेकिन, जैसा कि आप जानते हैं, हम दक्षता के प्रति बेचैन प्रतिभा हैं। बहुत कुछ क्यों, यदि पर्याप्त नहीं है - तो ऊपर वर्णित शेक्सपियर की शब्दावली का अनुमानित आकार केवल 128 बाइट्स मेमोरी का उपयोग करके गणना की जा सकती है।

विचार

हमेशा की तरह, हमें किसी प्रकार के हैश फ़ंक्शन की आवश्यकता है, तदनुसार, डेटा ही नहीं, बल्कि उनका हैश एल्गोरिथम के इनपुट पर आ जाएगा। हैश फ़ंक्शन का कार्य, जैसा कि आमतौर पर यादृच्छिक एल्गोरिदम में होता है, ऑर्डर किए गए डेटा को "यादृच्छिक" डेटा में बदलना है, जो मानों के डोमेन पर परिभाषा डोमेन के अधिक या कम समान प्रसार में है। परीक्षण के कार्यान्वयन के लिए, मैंने FNV-1a को एक अच्छा और सरल हैश फ़ंक्शन के रूप में चुना:

function fnv1a(text) { var hash = 2166136261; for (var i = 0; i < text.length; ++i) { hash ^= text.charCodeAt(i); hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24); } return hash >>> 0; } 

ठीक है, मस्तिष्क को चालू करें और उस बाइनरी को देखें जो इसे द्विआधारी प्रतिनिधित्व में देता है:

fnv1a('aardvark') = 1001100000000001110100100011001 1
fnv1a('abyssinian') = 00101111000100001010001000111 100
fnv1a('accelerator') = 10111011100010100010110001010 100
fnv1a('accordion') = 0111010111000100111010000001100 1
fnv1a('account') = 00101001010011111100011101011 100
fnv1a('accountant') = 0010101001101111110011110010110 1
fnv1a('acknowledgment') = 0000101000010011100000111110 1000
fnv1a('acoustic') = 111100111010111111100101011000 10
fnv1a('acrylic') = 1101001001110011011101011101 1000
fnv1a('act') = 0010110101001010010001011000101 1

आइए प्रत्येक हैश के लिए पहले नॉनजरो कम बिट के सूचकांक पर ध्यान दें, इस सूचकांक में एक जोड़ें और इसे रैंक (रैंक (1) = 1, रैंक (10) = 2, ...) कहें:

 function rank(hash) { var r = 1; while ((hash & 1) == 0 && r <= 32) { ++r; hash >>>= 1; } return r; } 

संभावना है कि हमारे पास 1 के रैंक के साथ एक हैश होगा 0.5, 2 के रैंक के साथ - 0.25, और आर के रैंक के साथ - 2 ^{- आर} । दूसरे शब्दों में, 2 ^आर हैश के बीच, रैंक आर के एक हैश को पूरा करना होगा। दूसरे शब्दों में, अगर हमें पता चला सबसे बड़ा आर रैंक है, तो 2 ^आर पहले से ही देखे जाने वाले अद्वितीय तत्वों की संख्या के मोटे अनुमान के रूप में फिट ^होगा ।

खैर, संभाव्यता का सिद्धांत एक ऐसी चीज है कि हम एक छोटे नमूने में एक बड़ी रैंक आर पा सकते हैं, या हम एक विशाल नमूने में एक छोटे से पा सकते हैं, और सामान्य तौर पर 2 ³¹ और 2 ³² में दो बड़े अंतर हैं, आप कहते हैं, और आप सही होंगे, यही कारण है कि ऐसा एकल अनुमान है बहुत अशिष्ट। क्या करें?

एक हैश फ़ंक्शन के बजाय, आप इनमें से एक बंडल का उपयोग कर सकते हैं, और फिर किसी तरह उनमें से प्रत्येक के लिए प्राप्त अनुमानों को "औसत" कर सकते हैं। यह दृष्टिकोण बुरा है क्योंकि हमें बहुत सारे कार्यों की आवश्यकता है और उन सभी पर विचार करना होगा। इसलिए, हम निम्नलिखित चाल करेंगे - हम प्रत्येक हैश के सबसे महत्वपूर्ण बिट्स को बंद कर देंगे और इन बिट्स के मूल्य को एक सूचकांक के रूप में उपयोग करते हुए, हम एक अनुमान नहीं, बल्कि 2 ^k रेटिंग की एक सरणी की गणना करेंगे, और फिर हम उनके आधार पर अभिन्न एक प्राप्त करेंगे।

HyperLogLog

वास्तव में, LogLog एल्गोरिथ्म के कई रूप हैं, हम अपेक्षाकृत हाल ही के विकल्प पर विचार करेंगे - HyperLogLog। यह संस्करण आपको मानक त्रुटि मान प्राप्त करने की अनुमति देता है:

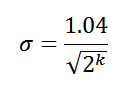
इसलिए, सूचकांक के रूप में 8 उच्च-क्रम बिट्स का उपयोग करते समय, हमें अद्वितीय तत्वों की सही संख्या के 6.5% ( 0.0 = 0.065) की मानक त्रुटि मिलती है। और सबसे महत्वपूर्ण बात, अगर आप पागल कौशल को संभाव्यता सिद्धांत से लैस करते हैं, तो आप निम्नलिखित अंतिम मूल्यांकन पर आ सकते हैं:

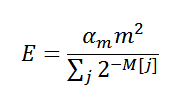
, जहां α _m करेक्शन गुणांक है, m कुल रेटिंग की संख्या (2 ^k ) है, M स्वयं अनुमानों की श्रेणी है। अब हम लगभग सब कुछ जानते हैं, यह कार्यान्वयन का समय है :

 var pow_2_32 = 0xFFFFFFFF + 1; function HyperLogLog(std_error) { function log2(x) { return Math.log(x) / Math.LN2; } function rank(hash, max) { var r = 1; while ((hash & 1) == 0 && r <= max) { ++r; hash >>>= 1; } return r; } var m = 1.04 / std_error; var k = Math.ceil(log2(m * m)), k_comp = 32 - k; m = Math.pow(2, k); var alpha_m = m == 16 ? 0.673 : m == 32 ? 0.697 : m == 64 ? 0.709 : 0.7213 / (1 + 1.079 / m); var M = []; for (var i = 0; i < m; ++i) M[i] = 0; function count(hash) { if (hash !== undefined) { var j = hash >>> k_comp; M[j] = Math.max(M[j], rank(hash, k_comp)); } else { var c = 0.0; for (var i = 0; i < m; ++i) c += 1 / Math.pow(2, M[i]); var E = alpha_m * m * m / c; // -- make corrections if (E <= 5/2 * m) { var V = 0; for (var i = 0; i < m; ++i) if (M[i] == 0) ++V; if (V > 0) E = m * Math.log(m / V); } else if (E > 1/30 * pow_2_32) E = -pow_2_32 * Math.log(1 - E / pow_2_32); // -- return E; } } return {count: count}; } function fnv1a(text) { var hash = 2166136261; for (var i = 0; i < text.length; ++i) { hash ^= text.charCodeAt(i); hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24); } return hash >>> 0; } var words = ['aardvark', 'abyssinian', ..., 'zoology']; // 2 336 words var seed = Math.floor(Math.random() * pow_2_32); // make more fun var log_log = HyperLogLog(0.065); for (var i = 0; i < words.length; ++i) log_log.count(fnv1a(words[i]) ^ seed); var count = log_log.count(); alert(count + ', error ' + (count - words.length) / (words.length / 100.0) + '%'); 

आइए हम अनुमान लगाएं कि हम कितनी मेमोरी का उपयोग कर रहे हैं, k 8 है, इसलिए, सरणी M में 256 तत्व होते हैं, उनमें से प्रत्येक, सशर्त रूप से, 4 बाइट्स लेता है, जो कुल मिलाकर 1 KB है। बुरा नहीं है, लेकिन मैं कम चाहूंगा। यदि आप इसके बारे में सोचते हैं, तो सरणी M से एकल अनुमान का आकार कम किया जा सकता है - आपको बस छत (log2 (32 + 1 - k )) बिट्स की आवश्यकता है, जो k = 8 के लिए, 5 बिट्स है। कुल मिलाकर, हमारे पास 160 बाइट्स हैं, जो पहले से ही काफी बेहतर है, लेकिन मैंने इससे भी कम का वादा किया था।

कम होने के लिए, हमारे डेटा में अधिकतम संभव अद्वितीय तत्वों की अधिकतम संख्या अग्रिम में जानना आवश्यक है - एन। वास्तव में, यदि हम इसे जानते हैं, तो रैंक निर्धारित करने के लिए हैश से सभी संभावित बिट्स का उपयोग करने की आवश्यकता नहीं है, छत (लॉग 2 ( एन / एम )) बिट्स पर्याप्त हैं। यह मत भूलो कि इस संख्या से हमें फिर से सरणी एम के एक तत्व का आकार प्राप्त करने के लिए लघुगणक लेने की आवश्यकता है ।

मान लीजिए कि, हमारे छोटे शब्दों के सेट के मामले में, उनकी अधिकतम संख्या 3,000 है, तो हमें केवल 64 बाइट्स की आवश्यकता है। शेक्सपियर के मामले में, हम एन को 100,000 के बराबर रखते हैं, और हमारे पास 6.5% की त्रुटि के साथ वादा किए गए 128 बाइट्स होंगे, 4.6% के साथ 192 बाइट्स, 3.3% के साथ 768। वैसे, शेक्सपियर की शब्दावली का वास्तविक आकार लगभग 30,000 शब्द है।

अन्य विचार

बेशक, छोटे "बाइट्स" का उपयोग करते हुए, उदाहरण के लिए, 3 बिट्स प्रदर्शन के मामले में बहुत कुशल नहीं हैं। व्यवहार में, बिट संचालन की लंबी श्रृंखलाओं के लिए पागल इमारत नहीं जाना बेहतर है, लेकिन वास्तुकला में मूल बाइट्स का उपयोग करना है। यदि आप अभी भी "पीसने" का निर्णय लेते हैं, तो मूल्यांकन को सही करने वाले कोड को सही करने के लिए मत भूलना।

एक छोटा चम्मच टार, त्रुटि sp अधिकतम त्रुटि नहीं है, लेकिन तथाकथित मानक त्रुटि है। हमारे लिए, इसका अर्थ है कि 65% परिणामों में 95, 95% से अधिक की त्रुटि होगी - 2 - और 99% से अधिक नहीं - 3 that से अधिक नहीं। यह काफी स्वीकार्य है, लेकिन हमेशा अपेक्षा से अधिक त्रुटि के साथ उत्तर पाने का मौका होता है।

मेरे प्रयोगों को देखते हुए, किसी को भी इसकी कमी को पूरा नहीं करना चाहिए, खासकर अगर बहुत कम डेटा की उम्मीद है। इस मामले में, सुधार प्रक्रिया शुरू होती है, जो हमेशा अपनी जिम्मेदारियों का सामना नहीं करती है। ऐसा लगता है कि एल्गोरिथ्म को किसी विशिष्ट कार्य के लिए परीक्षण और ट्यूनिंग की आवश्यकता होती है, जब तक कि निश्चित रूप से, यह मेरे कार्यान्वयन में कुछ बेवकूफाना गलती है। यह पूरी तरह सच नहीं है ।

32 बिट्स की चौड़ाई के साथ हैश फ़ंक्शन का उपयोग करते समय, एल्गोरिथ्म आपको लगभग 0.5% की न्यूनतम प्राप्य मानक त्रुटि के साथ 10 ⁹ अद्वितीय तत्वों की गणना करने की अनुमति देता है। इस तरह की त्रुटि के साथ, मेमोरी को लगभग 32-64 किबिट्स की आवश्यकता होती है। सामान्य तौर पर, LogLog लाइव डेटा स्ट्रीम के साथ ऑन-लाइन कार्य के लिए आदर्श है।

वह सब है। अलविदा!