 * अंग्रेजी से "बिना फ़िल्टर किए और फ़िल्टर किए गए अनुमान" ( Google अनुवाद द्वारा)Dmitriyn
* अंग्रेजी से "बिना फ़िल्टर किए और फ़िल्टर किए गए अनुमान" ( Google अनुवाद द्वारा)Dmitriyn के अनुरोध पर
, उन्होंने तथाकथित "Unscented Kalman filter" पर अपनी दृष्टि को प्रकाशित करने का फैसला किया, जो कि मामले में रैखिक Kalman फ़िल्टरिंग का विस्तार है जब सिस्टम के गतिशीलता और अवलोकन के समीकरण गैर-रैखिक होते हैं और पर्याप्त रूप से रेखीय नहीं किए जा सकते हैं।
जैसा कि इस निस्पंदन विधि का नाम
"कोषेर" है जो रूसी में पठनीय है, मुझे नहीं पता कि लेख के शीर्षक में क्या परिलक्षित होता है, इसलिए मैंने अपनी राय में, मशीनी अनुवाद में सिर्फ एक अजीब-सा कॉपी-पेस्ट करने का फैसला किया। अनुवाद का एक और मजेदार संस्करण एक
फजी फिल्टर है ।
UPD : "USING UT" अनुभाग में एक टिप्पणी जोड़ी गई
परिचय
रेखीय कलामन फ़िल्टरिंग पर
पिछले लेख में , एक गतिशील प्रणाली के रैखिक सरलीकृत गणितीय मॉडल के मामले के लिए फोटोनिक क्रिस्टल के संश्लेषण के संभावित तरीकों में से एक का वर्णन किया गया था। वहाँ वर्णित कलमन फ़िल्टर को कभी-कभी साहित्य में "पारंपरिक कलमन फ़िल्टर" कहा जाता है [
2 ]। उन्हें यह नाम इसलिए मिला, क्योंकि यह सबसे छोटी जड़-माध्य-वर्ग त्रुटि देता है, यदि कई परिकल्पनाएँ (रूढ़ियाँ) देखी जाती हैं - उदाहरण के लिए, शोर सफेद है और सामान्य कानून के अनुसार वितरित किया जाता है, शोर की उम्मीद शून्य है, चरण निर्देशांक के बीच शोर और क्रॉस-कनेक्शन के बीच कोई संबंध नहीं हैं। ये प्रतिबंध काफी गंभीर हैं और व्यवहार में अक्सर परिकल्पनाओं का उल्लंघन किया जाता है। इन प्रतिबंधों को दरकिनार करने की तकनीकें हैं (उदाहरण के लिए, चरण वेक्टर फ़िल्टर के लिए रंग शोर जनरेटर के लिए एक समन्वय फ़िल्टर को जोड़ने और "स्थानांतरित" शोर के लिए एक डमी गड़बड़ी का परिचय)। उन सभी को कम्प्यूटेशनल जटिलता (समस्या का आयाम बढ़ रहा है) में वृद्धि होती है और सम्मेलनों के उल्लंघन के लिए प्रतिरोधी एक फिल्टर के संश्लेषण में कठिनाइयों का सामना करना पड़ता है।
एक "एक्सटेंडेड कलमन फ़िल्टर" [
1 ] भी है, जो कि लीनियर वर्जन की संरचना के समान है, जिसमें यह बताया गया है कि डायनेमिक्स और अवलोकनों के समीकरणों में चरण निर्देशांक (नीचे दिए गए विवरण देखें) के कार्य गैर-रेखीय (पावर, त्रिकोणमितीय, आदि) होते हैं। यह अंतर चरण निर्देशांक (उदाहरण के लिए, दो निर्देशांक के उत्पाद) के बीच क्रॉस-लिंक की उपस्थिति का भी अर्थ है।
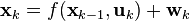
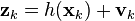
ईकेएफ का उपयोग करते समय, चरण निर्देशांक के आंशिक डेरिवेटिव के मैट्रिक्स, जैकबियन की गणना करने के लिए पुनरावृत्तियों के प्रत्येक चरण पर यह आवश्यक है। इस वजह से, कम्प्यूटेशनल जटिलता बहुत बढ़ जाती है और विच्छेदित अंतर समीकरणों की स्थिरता का सवाल और भी तेजी से उठता है। संक्षेप में, ईकेएफ एक नॉनलाइनियर डायनेमिक सिस्टम के रैखिककरण की एक परत को लागू करता है। यह मुख्य कारण है कि ईकेएफ अप्रभावी हो सकता है। एक डायनेमिक सिस्टम के दृढ़ता से नाइलिनियर मॉडल का उपयोग समस्या की एक बहुत खराब स्थिति की ओर जाता है, अर्थात। मापदंडों की स्थापना में छोटी सी त्रुटि। मॉडल बड़ी कम्प्यूटेशनल त्रुटियों को जन्म देंगे। नतीजतन, एल्गोरिदम मजबूती (त्रुटियों के प्रतिरोध) को खो देगा।
अनसेंटेड कलमन फ़िल्टर (यूकेएफ) [
3 ] एक अलग दृष्टिकोण ("अनसेन्टेड ट्रांसफॉर्म") लेता है।
विकिपीडिया के अनुसार, इस दृष्टिकोण से उम्मीद है कि वांछित वेक्टर के covariance और उस पर यादृच्छिक शोर के साथ डेटा के लिए नमूनों (सिग्मा अंक) के एक निश्चित न्यूनतम सेट का चुनाव किया जाता है। सिग्मा बिंदुओं का उपयोग करते हुए, गैर-रेखीय पूर्वानुमान कार्यों का निर्माण किया जाता है, जो तब क्रॉस-कोवरियन मैट्रिक्स (कलमन फ़िल्टरिंग एल्गोरिथ्म के कर्नेल) की गणना करने के लिए उपयोग किया जाता है।
अंतिम पैराग्राफ लिखने के बाद, मैंने व्यक्तिगत रूप से और भी अधिक प्रश्न किए। सेंट ऑगस्टीन की तरह, जो जानता था कि समय क्या था, जब तक कि उससे समय के बारे में नहीं पूछा गया। नीचे मैं अपने आप को और आपको स्पष्ट करने की कोशिश करूंगा, प्रिय पाठकों, विचार के तहत गैर-रेखीय फ़िल्टरिंग विधि का सार।
असंबद्ध परिवर्तन
शायद मैं एक रेखीय Kalman फ़िल्टर (FC) और गैर-रेखीय (विस्तारित, EFF) की दो मुख्य समस्याओं के अधिक विस्तृत वर्णन के साथ शुरू करूँगा। पहली समस्या हस्तक्षेप सम्मेलनों की है। जैसा कि ऊपर कहा गया है, रैखिक एफसी मानता है कि शोर "सफेद" है और सामान्य कानून के अनुसार वितरित किया गया है। यदि शोर "रंगीन" है, तो हमें एक डिजिटल शेपिंग फिल्टर को संश्लेषित करना चाहिए, जब "सफेद" शोर पास हो, जिसके माध्यम से हम वर्णक्रमीय विशेषता के साथ शोर प्राप्त करें (आदर्श रूप से) या मौजूदा डी फैक्टो के करीब। इस फिल्टर के चरण वेक्टर को FC के चरण वेक्टर में जोड़ा जाता है। यह बदले में समस्या के आयाम को बढ़ाता है। मान लीजिए यह समस्या बहुत गंभीर नहीं है। लेकिन एक दूसरा भी है - गणितीय मॉडल की गैर-शुद्धता की समस्या। ग़ैर-नियतता के कारण, हमें कुछ सन्निकट को लागू करना चाहिए जो हमें ग़ैर-रेखीय मैट्रिक्स फ़ंक्शन को रेखांकन करने की अनुमति देता है (ऊपर दिए समीकरण में "h" देखें) और इस प्रकार चरों को अलग करने की क्षमता प्रदान करता है। चर को अलग किया जाना चाहिए ताकि चरण वेक्टर के घटकों के लिए समीकरण बनाना संभव हो। ईकेएफ में, जैकोबियन की गणना करके रैखिककरण किया जाता है, अर्थात। "h" आंशिक समीकरण में प्रत्येक समीकरण के लिए चरण चर में से प्रत्येक के लिए गणना की जाती है। अपने आप में यह ऑपरेशन पहले से ही एक समस्या है - बड़ी मात्रा में संगणना। इसके अलावा, जैकबियन की गणना के लिए, फॉर्म के टेलर श्रृंखला विस्तार (बहुआयामी) का उपयोग किया जाता है:

इस मामले में, केवल श्रृंखला के पहले सदस्य को लिया जाता है, और बाकी को नगण्य माना जाता है। इस प्रकार, इस रैखिककरण का उपयोग करते हुए, हम फॉर्म की एक अभिव्यक्ति प्राप्त करते हैं:
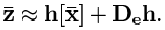
इस समीकरण में, "डी" मैट्रिक्स फ़ंक्शन के कुल अंतर की गणना करने का ऑपरेटर है।
यदि गणितीय मॉडल की अशुद्धता छोटी है (मॉडल लगभग रैखिक है), तो इस कथन को सच माना जा सकता है। हालांकि, व्यवहार में, मॉडल की गैर-भिन्नताएं ऐसी हैं कि वे दूसरे और / या अधिक छोटेपन के आदेश के विस्तार की शर्तों को त्यागने की अनुमति नहीं देते हैं। ऐसे मामलों में, ईकेएफ में रैखिककरण एक कम्प्यूटेशनल त्रुटि उत्पन्न करता है, जिसे उपेक्षित नहीं किया जा सकता है। कुछ विशेष मामलों में, टेलर श्रृंखला में विस्तार किए बिना करना संभव है, लेकिन ये विशेष समाधान हैं जो कठोर रूप से एक विशिष्ट वस्तु से बंधे हैं। एक समाधान भी है जो टेलर श्रृंखला को लघुता [6] के दूसरे क्रम के कार्यकाल में विभाजित करता है। इसमें हेसियन की गणना शामिल है, जो दूसरे क्रम के डेरिवेटिव के एक दसवें हिस्से में है। बस प्लीज, मुझे चबाओ मत कि यह क्या है। यह महसूस करना पर्याप्त है कि यह ईकेएफ को अधिक कठिन बनाता है और इसके कार्यान्वयन को जटिल बनाता है।
तो, एक एफसी को किसी वस्तु के नॉनलाइनियर मॉडल पर लागू किया जा सकता है यदि एक निश्चित परिवर्तन ज्ञात है जो आपको अगले पुनरावृत्ति चरण में चरण वेक्टर के वर्तमान मूल्य ("नॉनलाइनियर" पूर्वानुमान) बनाने की अनुमति देता है। यदि इस तरह का (पर्याप्त) परिवर्तन अज्ञात है, तो हम इसके साथ ईकेएफ का उपयोग करते हैं, अक्सर अपर्याप्त, रैखिककरण और बहुत बड़े कम्प्यूटेशनल भार भी। इस प्रकार, हमें एक ऐसी विधि की आवश्यकता है जो ईकेएफ में उपयोग किए गए रैखिककरण के बिना कर सकती है, और ईकेएफ की तुलना में अधिक कम्प्यूटेशनल जटिलता नहीं है। यह विधि अनसेन्टेड ट्रांसफ़ॉर्मेशन है (UT, आगे इस संक्षिप्त नाम को कंप्यूटर गेम के साथ भ्रमित न करें)।
यूटी का मुख्य विचार सहज धारणा के तहत
अधिक फ़्रैग इकट्ठा करना है कि एक नॉनज़रो अपेक्षा के साथ यादृच्छिक चर की प्रायिकता वितरण फ़ंक्शन को अनुमानित करना बहुत आसान है (जो कि हमारा चरण वेक्टर है - एक यादृच्छिक शोर उस पर आरोपित किया गया है जो कुछ मनमाने नॉनलाइनर ट्रांसफ़ॉर्मेशन फ़ंक्शन को अनुमानित करता है। यह तकनीक पैरामीटर स्पेस (चरण निर्देशांक) में अंक (सिग्मा पॉइंट) के एक सेट की एक विशेष विधि द्वारा चयन का तात्पर्य करती है, जो कि वांछित यादृच्छिक वेक्टर (हमारे मामले में, चरण वेक्टर के साथ पर्याप्त विशेषताओं के साथ सांख्यिकीय विशेषताओं (अपेक्षा, भिन्नता और उच्च आदेश के अन्य पल विशेषताओं) की विशेषता है। एक शोर वेक्टर द्वारा आरोपित)। इन बिंदुओं का चयन करने के लिए, प्रपत्र के भावों का उपयोग किया जाता है:
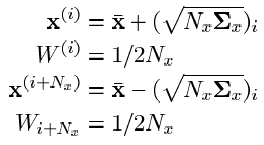
इन अभिव्यक्तियों में, "
एनएक्स " वांछित चरण वेक्टर का आयाम है; "
मैं " सिग्मा बिंदु (i = 1 ..
Nx ) का सूचकांक है; "
वाई "
i- वें सिग्मा बिंदु का वजन है;
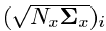
-
मैं चरण वेक्टर के आयाम द्वारा गुणा किए गए मॉडल के प्रारंभिक nonlinear परिवर्तन के सहसंयोजक मैट्रिक्स के मैट्रिक्स वर्गमूल का स्तंभ।
यह ध्यान दिया जाना चाहिए कि सिग्मा बिंदुओं के सेट के लिए यह एकमात्र विकल्प नहीं है। उपरोक्त अभिव्यक्तियाँ केवल पहले और दूसरे क्षण (अपेक्षा और विचरण) के लिए वितरण के आंकड़ों को विशिष्ट रूप से चिह्नित करती हैं। यूटी, जो उच्चतर आदेशों के क्षणों तक वांछित वेक्टर के वितरण के आंकड़ों की विशेषता है, सिग्मा बिंदुओं की संख्या में भिन्नता है (आम तौर पर बोलना, उनकी संख्या आवश्यक रूप से ऊपर के भावों से अधिक नहीं होगी) और वेट की पसंद। सादगी के लिए, मैं विवरण को छोड़ देता हूं। मैं केवल एक उदाहरण के रूप में यूटी के लिए अभिव्यक्ति दूंगा, चरण वेक्टर के वितरण के आंकड़ों के क्षणों के उच्च आदेशों को ध्यान में रखते हुए:
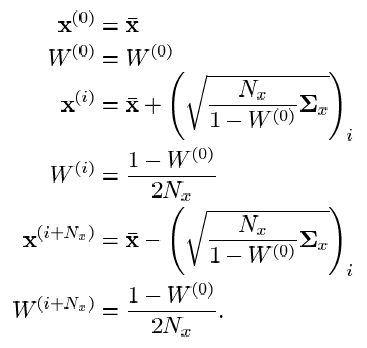
सिद्धांत रूप में, यूटी के बारे में, संक्षेप में, सब कुछ। इसकी आवश्यकता क्यों है और यूकेएफ में इसका उपयोग कैसे किया जाता है, नीचे लिखा गया है। यह उच्च आदेशों की पल विशेषताओं के बारे में एक आरक्षण बनाने के लिए बनी हुई है। यह क्या है एक सहज सादृश्यता एक गतिशील शरीर की स्थिति, गति और त्वरण है। यदि हम स्थिति को पहले क्रम के क्षण के रूप में मानते हैं, तो गति दूसरे क्षण (स्थिति के परिवर्तन की दर), और त्वरण - तीसरा (गति के परिवर्तन की दर) होगी। आप त्वरण के व्युत्पन्न की गणना कर सकते हैं - हमें चौथा क्षण मिलता है। लेकिन क्या यह व्यावहारिक समझ में आता है? इसी तरह आँकड़ों में पल-पल की विशेषताओं के साथ - ज्यादातर मामलों में, अपेक्षा और भिन्नता पर्याप्त है। UT की सांख्यिकीय सटीकता से, अर्थात फ़िल्टरिंग दक्षता सिग्मा बिंदुओं को चुनने की विधि पर निर्भर करती है, लेकिन निश्चित रूप से इतना नहीं है कि अधिकांश व्यावहारिक समस्याओं के लिए उच्च आदेशों की पल-पल की विशेषताओं को ध्यान में रखना चाहिए।
UT आवेदन
जैसा कि ऊपर उल्लेख किया गया है, यूटी एक ऐसी विधि है जो आपको नॉनलाइनियर स्टोचैस्टिक आकलन में रैखिककरण प्रक्रिया से छुटकारा पाने की अनुमति देती है। अब तक, हमने केवल यह सीखा है कि यूटी की मदद से उन बिंदुओं का एक सेट चुनना संभव है जो वांछित वेक्टर (चरण वेक्टर) के आंकड़ों को सटीक रूप से चिह्नित करते हैं। यह हमें क्या देता है? कलमन फ़िल्टरिंग में मुख्य बिंदु क्रॉस-कोवरियन मैट्रिक्स की गणना है (
पिछले लेख में केके मैट्रिक्स
देखें )। रैखिक FC में इस मैट्रिक्स की गणना मैट्रिक्स Riccati समीकरण के समाधान के रूप में की जाती है। नॉनलाइन मैट के मामले में। सिस्टम मॉडल, यह प्रक्रिया बहुत जटिल है। यूटी आपको वैकल्पिक तरीके से क्रॉस-कोवरियन मैट्रिक्स प्राप्त करने की अनुमति देता है। निम्नलिखित UT विधि का उपयोग करके चरण-दर-चरण फ़िल्टरिंग प्रक्रिया है।
- हम वांछित वेक्टर (चरण वेक्टर या अवलोकन वेक्टर - सेंसर के आउटपुट संकेतों के वेक्टर) के सांख्यिकीय पैरामीटर पाते हैं। प्राप्त सांख्यिकीय विशेषताओं को वास्तविक समय में निरंतर या अद्यतन माना जा सकता है।
- प्राप्त आंकड़ों के आधार पर, हम सिग्मा बिंदुओं के एक सेट की गणना करते हैं।
- हम मूल nonlinear चटाई के माध्यम से इन बिंदुओं को पारित करते हैं। गतिशील प्रक्रिया मॉडल:
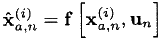
- हम उम्मीद और कोविर्स के पूर्वानुमान की गणना करते हैं:

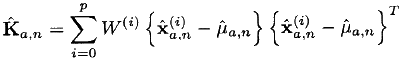
- हम अवलोकन मॉडल के माध्यम से तीसरे चरण में प्राप्त अंक (सामान्य मामले में, गैर-रैखिक भी) पास करते हैं:

- हम अवलोकन के पूर्वानुमान की गणना करते हैं (पिछले चरण में मूल्यों के भारित औसत के रूप में):
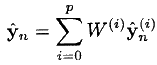
- हम अवलोकन के सहसंयोजक की गणना करते हैं:
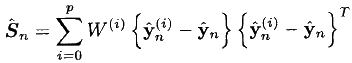
- हम आवश्यक क्रॉस-कोवरियन मैट्रिक्स को ढूंढते हैं:
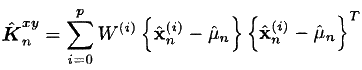
- अंत में, हम मानक FC अभिव्यक्तियों का उपयोग करते हैं:

अभिव्यक्तियों के अंतिम ब्लॉक को लेख [3] से कॉपी किया जाता है। मेरी राय में, उसके साथ कुछ गलत है। यह स्पष्ट नहीं है कि क्रायज़ के बिना "yn" और बिना पहचान चिह्न के क्रॉस-कोवरियन मैट्रिक्स कहाँ से आया है। लेकिन इससे कोई फर्क नहीं पड़ता। "एफसी के मानक भाव" के बारे में मैंने पहले ही लिखा था। आपको बस कल्टमैन के UT के माध्यम से प्राप्त मैट्रिक्स लाभ (उर्फ क्रॉस-कोवरियन मैट्रिक्स) में स्थानापन्न करना है और चरण वेक्टर के सही अनुमान की गणना करना है।
चरण वेक्टर के बारे में एक और टिप्पणी। उपर्युक्त अभिव्यक्तियों में सूचकांक "ए" (एक्सए, एन) के साथ एक चरण वेक्टर है - यह प्रक्रिया और अवलोकन शोर के लिए पूरक (संवर्धित) निर्देशांक के साथ पूरक एक चरण वेक्टर है। शुरुआत में, मैंने लिखा था कि हस्तक्षेप की वर्णक्रमीय विशेषता पर प्रतिबंधों को दरकिनार करने के लिए एक ऐसी तकनीक है। तो, उपरोक्त अभिव्यक्तियों में, सामान्य वैक्टर से संवर्धित संक्रमण किसी तरह चुपचाप किया जाता है (एक "म्यू" उम्मीद भी है जो सरल और संवर्धित है)।
निष्कर्ष
इसलिए, यूटी की मदद से, हम चरण वेक्टर और क्रॉस-कोवरियन मैट्रिक्स के पूर्वानुमान की गणना करने के लिए, रेखीयकरण के बिना, सक्षम थे। एफसी पूर्वानुमान के सुधार चरण के लिए मानक भावों में उनके मूल्यों को प्रतिस्थापित करते हुए (रैखिक एफसी पर लेख में "मापन अपडेट" देखें), हमने चरण वेक्टर के अनुमान प्राप्त किए। इस मामले में सबसे अधिक संसाधन-गहन प्रक्रिया मैट्रिक्स वर्गमूल की गणना सिग्मा बिंदुओं के एक सेट के निर्माण में होती है। यूकेएफ की समग्र जटिलता ईकेएफ से अधिक नहीं है। यूकेएफ के मुख्य लाभ विभिन्न कार्यों के लिए संश्लेषण की व्यापकता है (संश्लेषण प्रक्रिया इस बात पर निर्भर नहीं करती है कि आप किस वस्तु के साथ काम कर रहे हैं), साथ ही परिणामी एल्गोरिथ्म की स्थिरता (यूटी की संख्यात्मक स्थिति ईकेएफ में रैखिककरण प्रक्रिया की स्थिति से अधिक है) और प्राप्त अनुमानों में पूर्वाग्रह की अनुपस्थिति (फिर से, के कारण) रैखिककरण की अस्वीकृति के लिए)। एक दृष्टांत के रूप में, मैं लेख [3] (अनुमान 1 देखें) से अनुमान त्रुटियों का ग्राफ दूंगा।
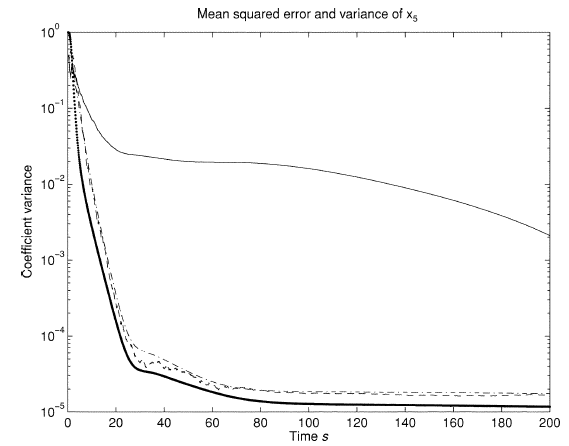
अंजीर। 1. ईकेएफ और यूकेएफ के लिए आरएमएस त्रुटि और अनुमान भिन्नता भूखंड
इस आकृति में, पतली रेखा EKF (माध्य-वर्गीय त्रुटियों) के लिए माध्य वर्ग त्रुटि है। स्कैटर प्लॉट (बोल्ड, एट द बॉटम) - अनुमानित कोविरियन। दो अन्य रेखांकन यूकेएफ के लिए हैं। ईकेएफ में कम कोवरियस अंक हैं (यह कुछ हद तक बेहतर होता है), लेकिन इसके स्कोर में आरएमएसई बहुत अधिक है। यूकेएफ सहसंयोजक और मानक विचलन लगभग समान स्तर पर हैं। वैसे, यह मुझे लग रहा था कि किसी तरह की गलती थी। फैलाव मानक विचलन का वर्ग है। वे एक साथ कैसे हो सकते हैं? यहाँ, या तो मैंने शब्दों की गलत व्याख्या की (ऊपर के कोष्ठकों में उद्धृत), या, फिर भी, सहसंयोजकों और मानक विचलन के अनुमान अलग-अलग हैं।
यूपीडी मैं यह भी नोट करना चाहता हूं कि मैं खुद अभी तक पूरी तरह से समझ नहीं पाया हूं कि यह विधि कैसे काम करती है, और क्या मैंने इसके सार को सही ढंग से समझा है। मैं इसे लागू करने की कोशिश करूंगा - यह वास्तव में लागू करने के लिए एक सरल एल्गोरिथ्म की तरह लगता है। मैं देखूंगा कि वह खुद को कैसे दिखाता है, समय कैसा होगा।
इस बीच, आपके विचार, सुझाव, टिप्पणियाँ ... और ध्यान के लिए धन्यवाद!
संदर्भ:
- विकी पर यूकेएफ
- नॉनलाइनर सिग्मा पॉइंट कलामन फ़िल्टर का उपयोग करके कक्षा निर्धारण से संबंधित एक चर्चा
- जूलियर, एसजे; उहल्मन, जेके (1997)। "नॉनलाइन सिस्टम के लिए कलमन फ़िल्टर का एक नया विस्तार।" इंट। संगोष्ठी। एयरोस्पेस / डिफेंस सेंसिंग, सिमुल। और नियंत्रण 3. 2008-05-03 को लिया गया।
- फजी मजबूत ट्रैकिंग असंतुलित कलामन फ़िल्टर
- अप्रकाशित रूपांतरण
- एम। अथान्स, आरपी विशनर, और ए। बर्टोलिनी, "सबोप्टीमल राज्य
असतत से निरंतर समय के लिए nonlinear सिस्टम का अनुमान
शोर माप, “आईईईई ट्रांस। आटोमैटिक। कॉन्ट्र।, वॉल्यूम। एसी -13,
पीपी। 504-518, अक्टूबर। 1968।