एन पहला प्राइम नंबर खोजने के लिए एल्गोरिथ्म - एटकिन चलनी

एक कार्यक्रम को लागू करने की प्रक्रिया में, मुझे क्रम संख्या N तक की प्राइमर खोजने के कार्य के साथ सामना करना पड़ा । पहले से ही कई तरीकों और तरीकों के बारे में बार-बार लिखा गया था, लेकिन उस फैसले के मुख्य तरीके के बारे में नहीं बताया, जिसे मैं आज ठीक करने की कोशिश करूंगा।



एल्गोरिथ्म में असममित जटिलता है और आवश्यकता है थोड़ी याददाश्त। इनपुट ऑर्डर मानों पर एट्रस्टेन चलनी की तुलना में एटकिन चलनी 9.2 गुना तेज है। मैं 2 से संख्याओं पर Atkin एल्गोरिथ्म की श्रेष्ठता के विकास का एक ग्राफ देता हूँ :



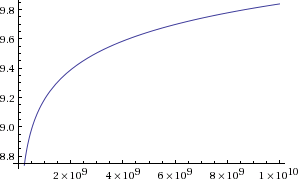
परिणामस्वरूप, निम्नलिखित निष्पादन गति देखी जा सकती है:

10000000	0.15 सेकंड
100000000	2.16 सेकंड
1000000000	48.76 सेकंड

सुविधा और संक्षिप्तता के लिए, हम एक अमूर्त वर्ग बनाएंगे, जहाँ से हम एटकिन चलनी के कार्यान्वयन को प्राप्त करेंगे। भविष्य में, हम केवल विभिन्न वर्ग वेरिएंट बनाएंगे।

public abstract class AAtkin
{
internal readonly int _limit;
public bool [] IsPrimes;

protected AAtkin( int limit)
{
_limit = limit;
FindPrimes();
}

public abstract void FindPrimes();
}


आइए एल्गोरिथ्म का एक बुनियादी कार्यान्वयन बनाएं:

public override void FindPrimes()
{
IsPrimes = new bool [_limit + 1];
double sqrt = Math .Sqrt(_limit);
var limit = ( ulong ) _limit;
for ( ulong x = 1; x <= sqrt; x++)
for ( ulong y = 1; y <= sqrt; y++)
{
ulong x2 = x*x;
ulong y2 = y*y;
ulong n = 4*x2 + y2;
if (n <= limit && (n%12 == 1 || n%12 == 5))
IsPrimes[n] ^= true ;

n -= x2;
if (n <= limit && n%12 == 7)
IsPrimes[n] ^= true ;

n -= 2 * y2;
if (x > y && n <= limit && n%12 == 11)
IsPrimes[n] ^= true ;
}

for ( ulong n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
ulong s = n*n;
for ( ulong k = s; k <= limit; k += s)
IsPrimes[k] = false ;
}
IsPrimes[2] = true ;
IsPrimes[3] = true ;
}


एल्गोरिथ्म के मूल (क्लासिक) संस्करण का निष्पादन समय:

1000000	0.03 सेकंड
10000000	0.39 सेकंड
100000000	4.6 सेकंड
1000000000	48.92 सेकंड

स्मरण करो कि C # में, ulong प्रकार के साथ संचालन, int प्रकार की तुलना में लगभग 3 गुना अधिक समय लेता है। कार्यक्रम में, बड़ी संख्या की गणना करते समय, मान अभी भी int.MaxValue से अधिक है, इसलिए हम एक अनुभवजन्य उपयोग पट्टी पाएंगे। यहां यह 858599509 है। शर्त लगाएं और अंतिम त्वरण प्राप्त करें:

IsPrimes = new bool [_limit + 1];
double sqrt = Math .Sqrt(_limit);
if (sqrt < 29301)
{
for ( int x = 1; x <= sqrt; x++)
for ( int y = 1; y <= sqrt; y++)
{
int x2 = x * x;
int y2 = y * y;
int n = 4 * x2 + y2;
if (n <= _limit && (n % 12 == 1 || n % 12 == 5))
IsPrimes[n] ^= true ;

n -= x2;
if (n <= _limit && n % 12 == 7)
IsPrimes[n] ^= true ;

n -= 2 * y2;
if (x > y && n <= _limit && n % 12 == 11)
IsPrimes[n] ^= true ;
}

for ( int n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
int s = n * n;
for ( int k = s; k <= _limit; k += s)
IsPrimes[k] = false ;
}
}
else
{
var limit = ( ulong ) _limit;
for ( ulong x = 1; x <= sqrt; x++)
for ( ulong y = 1; y <= sqrt; y++)
{
ulong x2 = x*x;
ulong y2 = y*y;
ulong n = 4*x2 + y2;
if (n <= limit && (n%12 == 1 || n%12 == 5))
IsPrimes[n] ^= true ;

n -= x2;
if (n <= limit && n%12 == 7)
IsPrimes[n] ^= true ;

n -= 2 * y2;
if (x > y && n <= limit && n%12 == 11)
IsPrimes[n] ^= true ;
}

for ( ulong n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
ulong s = n*n;
for ( ulong k = s; k <= limit; k += s)
IsPrimes[k] = false ;
}
}
IsPrimes[2] = true ;
IsPrimes[3] = true ;
}


वह सब है। आपके ध्यान के लिए धन्यवाद - मैंने कोशिश की कि यह बहुत सूखा न हो।