एक हेक्सागोनल ग्रिड पर एक रास्ता खोजना

वास्तव में, मैंने किसी के लिए कुछ भी नया नहीं बताया है, लेकिन जो मैंने पाया वह मुश्किल गणित के साथ था (अधिक सटीक रूप से, इतना मुश्किल नहीं, लेकिन फिर भी मेरे लिए व्यक्तिगत रूप से समझना मुश्किल है), और यहाँ यह मेरी अपनी सरल बाइक लग रही थी।

और इसलिए हमारे पास पहले से ही:
एक नियमित आयताकार ग्रिड पर खोजें।
हमें क्या चाहिए:
न्यूनतम प्रयास के साथ हेक्सागोनल ग्रिड खोजें।

सामान्य ग्रिड संरचना

पहला विचार यह है कि कॉलम के माध्यम से सबकुछ शिफ्ट किया जाए:

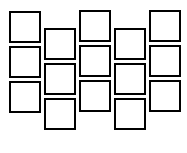
फिर वर्तमान सेल के पड़ोसी कुछ इस तरह दिखते हैं:

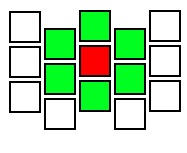
जैसा कि आप देख सकते हैं, सिद्धांत में कोशिकाओं के बीच संबंध सिर्फ हेक्स के रूप में होना चाहिए:

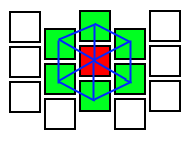
लेकिन तुरंत इस बात पर संदेह होता है कि इसमें वर्ग नहीं होना चाहिए, लेकिन आयतें:

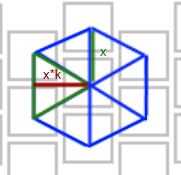
यह गणना करना मुश्किल नहीं है कि आकृति में k का आकार sqrt (3) / 2 के बराबर होगा
नतीजतन, हमें एक ग्रिड मिलता है

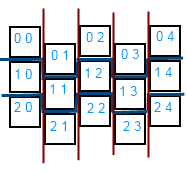
जहां प्रत्येक कोशिका का आकार क्रमशः w = sqrt (3) / 2, h = 1 होता है, जबकि प्रत्येक विषम कॉलम (यदि आप 0 से गिनना शुरू करते हैं) 0.5 से स्थानांतरित कर दिया जाता है

समन्वय में परिवर्तन

फिर सब कुछ सेल नंबर में निर्देशांक का अनुवाद करना आसान हो जाता है, सम-विषम कॉलम के लिए समायोजित:
(x,y)=>(x/w, (y-(x/w)%2)/h)
इसके विपरीत, फ़ील्ड सेल को निर्देशांक में अनुवाद करें:
(i,k)=>(i*w, k*h+h/2*(i%2))

पड़ोसी

अब हमें चयनित सेल के सभी पड़ोसियों को प्राप्त करने की आवश्यकता है।
वे कॉलम (और विषम कॉलम के लिए सममित) के लिए कुछ इस तरह दिखेंगे।


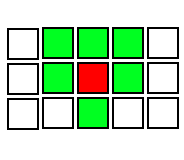
(i,k)=>(
(i+1,k),
(i-1,k),
(i,k+1),
(I,k-1),
(i+1,k+(1-2*i%2)),
(i-1,k+(1-2*i%2)))


दो कोशिकाओं के बीच की दूरी

अब, एक पूर्ण कार्यान्वयन के लिए, केवल दो कोशिकाओं के बीच की दूरी का पता लगाने की कमी है, बेशक आप तुच्छ यूक्लिडियन का उपयोग कर सकते हैं, लेकिन यह हमारा विकल्प नहीं है। बुनियादी आधार के लिए, हम एक नियमित ग्रिड पर विकर्ण दूरी लेते हैं:
xd = abs(p1.X - p2.X);
yd = abs(p1.Y - p2.Y);
diagonal = min(xd, yd);
straight = xd + yd;
result = sqrt(2) * diagonal + (straight - (2 * diagonal)));


हमारी स्थिति समान है (वहाँ भी विकर्ण चालें हैं), केवल लंबवत स्थानांतरित करने के लिए (उदाहरण के रूप में ग्रिड के उन्मुखीकरण को देखते हुए), आप या तो एक कदम खड़ी या 2 क्षैतिज रूप से ले सकते हैं।
//
if (xd >= yd * 2)
{
result = xd;
}
//
else
{
result = xd + (yd – xd/2);
}

लेकिन यहां एक छोटा सा विवरण है, अगर दूरी को विभिन्न स्तंभों से दो कोशिकाओं के बीच मापा जाता है, तो सेल के फर्श में एक बेहिसाब विस्थापन होगा। इसलिए, yd को थोड़ा अलग तरीके से परिभाषित किया जाना चाहिए:
yd =abs((p1.Y + (p1.X%2)/2) – (p2.Y + (p2.X%2)/2));

अब यह सभी पर ए * सेट करने के लिए रहता है, उदाहरण के लिए, जैसा कि मैंने यहां किया था, और तदम:

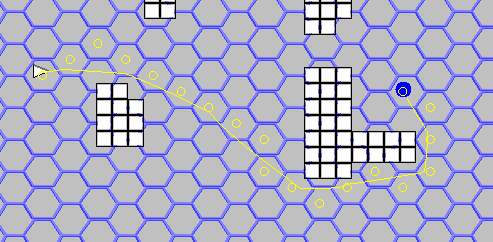
एक आफ्टरवर्ड के बजाय

बेशक, हेक्सागोनल ग्रिड में हेरफेर करने के लिए अधिक सुंदर गणितीय विधियां हैं, लेकिन मेरी राय में यह विधि जीवन के अधिकार के लिए काफी सरल हो गई (और प्रदर्शन परीक्षण में प्लस ने काफी अच्छे परिणाम दिखाए)।