NetworkX लाइब्रेरी को जटिल नेटवर्क संरचनाओं की संरचना, गतिशीलता और कार्यप्रणाली के निर्माण, हेरफेर और अध्ययन के लिए माना जाता है ।
पुस्तकालय को सीखने के उपकरण, अनुप्रयुक्त प्रोग्रामिंग या अनुसंधान के रूप में उपयोग करने की मूल बातें मानी जाती हैं।
पुस्तकालय के विवरण के लिए आधार साइट से आधिकारिक सामग्री हैं।
लाइब्रेरी 1.5 का संस्करण माना जाता है।

पुस्तकालय सुविधाएँ

नेटवर्कएक्स लाइब्रेरी को पायथन में बनाया गया था और इसे ग्राफ़ और अन्य नेटवर्क संरचनाओं के साथ काम करने के लिए डिज़ाइन किया गया है। यह नए बीएसडी लाइसेंस के तहत वितरित मुफ्त सॉफ्टवेयर है।
पुस्तकालय की मुख्य विशेषताएं:

• सरल, उन्मुख और भारित रेखांकन के साथ काम करने के लिए कक्षाएं;
• एक नोड लगभग कुछ भी हो सकता है: समय-श्रृंखला, पाठ, छवि, एक्सएमएल;
• सबसे आम ग्राफ़ स्टोरेज फ़ाइल स्वरूपों से / के लिए ग्राफ़ को सहेजना / लोड करना;
• बुनियादी प्रकार के रेखांकन बनाने के लिए अंतर्निहित प्रक्रियाएं;
• सबग्राफ, क्लिक्स और के-पार्टाइट ग्राफ़ (K-core) (अधिकतम सबग्राफ जिसमें प्रत्येक शीर्ष पर कम से कम स्तर K है) का पता लगाने के तरीके।
• रेखांकन, ग्राफ ऊंचाई, व्यास, त्रिज्या, पथ की लंबाई, केंद्र, मध्यवर्तीता आदि के रूप में एक ग्राफ की ऐसी विशेषताओं को प्राप्त करना।
• 2D और 3D ग्राफ़ के रूप में विज़ुअलाइज़ नेटवर्क;
• और बहुत कुछ ...

उत्पादकता

यह कहा जाता है कि पुस्तकालय बहुत बड़ी नेटवर्क संरचनाओं के साथ संचालित करने के लिए स्वतंत्र है, एक ग्राफ स्तर 10 मिलियन नोड्स और उनके बीच 100 मिलियन आर्क्स। इस तथ्य के मद्देनजर कि यह पायथन भाषा की एक निम्न-स्तरीय डेटा संरचना पर आधारित है, जिसे "डिक्शनरी डिक्शनरी" कहा जाता है, मेमोरी का कुशलता से उपयोग किया जाता है, ग्राफ पैमाने पर अच्छी तरह से, उस ऑपरेटिंग सिस्टम की विशेषताओं पर बहुत कम निर्भर करता है जिसमें स्क्रिप्ट निष्पादित की जाती है, और वर्तमान में लोकप्रिय विश्लेषण क्षेत्र के लिए उत्कृष्ट है। सामाजिक नेटवर्क और ग्राफ से डेटा ।

बुनियादी डेटा संरचनाएँ

पुस्तकालय संकुल के पदानुक्रम के रूप में व्यवस्थित है। प्रत्येक पैकेज में ऊपरी स्तर इसकी संरचनाओं में हेरफेर करने के लिए सामान्य तरीके प्रदान करता है, निचले वाले अधिक से अधिक विशेषज्ञता हासिल करते हैं।
निम्नलिखित सभी उदाहरणों में, नेटवर्कएक्स निम्नलिखित निर्देश के साथ जुड़ा हुआ है:

>>> import networkx as nx 

कक्षा का ग्राफ

निम्नलिखित मुख्य प्रकार के ग्राफ़ समर्थित हैं:

• ग्राफ एक सरल अप्रत्यक्ष ग्राफ का कार्यान्वयन है। दो नोड्स के बीच अतिरिक्त झुकावों को नजरअंदाज किया जाता है, खुद से जुड़े नोड्स संभव हैं।
• DiGraph एक निर्देशित ग्राफ़ है, इस प्रकार के ग्राफ़ के लिए विशिष्ट कार्य और प्रतिबंध जोड़े गए हैं।
• मल्टीग्राफ - मल्टीग्राफ का कार्यान्वयन, इस तरह के रेखांकन ग्राफ़ में वर्टिस के जोड़े हो सकते हैं जो एक से अधिक किनारे (गैर-दिशात्मक), या विपरीत दिशाओं के दो से अधिक आर्क से जुड़े होते हैं।
• MultiDiGraph एक उपयुक्त रूप से उन्मुख मल्टीग्राफ है।

विभिन्न प्रकार के खाली ग्राफ़ बनाने के उदाहरण:

 >>> G=nx.Graph() >>> G=nx.DiGraph() >>> G=nx.MultiGraph() >>> G=nx.MultiDiGraph() 

ग्राफ़ का आंतरिक प्रतिनिधित्व आसन्न सूचियों के रूप में कार्यान्वित किया जाता है। हालांकि, असंगति से बचने के लिए, रेखांकन के साथ सभी कार्यों को सीधे इस सूची के साथ नहीं किया जाना चाहिए, लेकिन लाइब्रेरी फ़ंक्शन एपीआई का उपयोग करना चाहिए।

समुद्री मील और चाप

किसी भी ग्राफ के घटक। किसी भी नोड या आर्क में एक विशिष्ट पहचानकर्ता होता है जिसके द्वारा आप इससे जुड़ी सभी जानकारी प्राप्त कर सकते हैं, और इसके अलावा पहचानकर्ताओं की तुलना में वर्तमान एल्गोरिथ्म को लागू करने के लिए अधिक सुविधाजनक नाम हो सकते हैं जो आपको यह डेटा प्राप्त करने की अनुमति देते हैं।
इसके अतिरिक्त, प्रत्येक नोड या चाप में विभिन्न प्रकार के डेटा को संग्रहीत करने की कोई भी संख्या हो सकती है। भारित ग्राफ़ में "वेट" नामक एक सेवा विशेषता होती है और इस नाम का उपयोग अन्य सूचनाओं को संग्रहीत करने के लिए नहीं किया जा सकता है ताकि इसके प्रतिनिधित्व के आंतरिक तर्क को नष्ट न किया जा सके।

ग्राफ निर्माण

फिलहाल, तीन तरीकों में से एक का उपयोग करके एक ग्राफ बनाया जा सकता है:

• 1. ग्राफ जनरेटर - सामान्य टोपोलॉजी के ग्राफ बनाने के लिए पूर्वनिर्धारित कक्षाएं, जैसे कि विभिन्न स्तरों के पूर्ण रेखांकन, संतुलित पेड़, चक्रीय ग्राफ, डोरोगोवत्सेव-गोल्टसेव-मेंडेस ग्राफ, यादृच्छिक द्विपद और कई अन्य प्रकार। अधिक के लिए प्रलेखन देखें: networkx.lanl.gov/reference/generators.html
• 2. डेटा लोड हो रहा है और एक समर्थित स्वरूपों की एक फ़ाइल या डेटा स्ट्रीम के आधार पर ग्राफ पीढ़ी:
  
  1. आसन्न मैट्रिक्स
  2. घटना मैट्रिक्स
  3. GEXF
  4. GML
  5. अचार
  6. GraphML
  7. LEDA
  8. YAML
  9. SparseGraph6
  10. Pajek
  11. जीआईएस शेपफाइल
  
  
• 3. नोड्स और आर्क्स का क्रमिक जोड़।

बनाए गए ग्राफ़ में सामान्य और विधि-विशिष्ट दोनों तरीके हैं।

 >>> import networkx as nx >>> G=nx.Graph() >>> G.add_edge(1,2) #       = 1 >>> G.add_edge(2,3,weight=0.9) #    

जोड़े गए मान विभिन्न प्रकारों के डेटा की सेवा कर सकते हैं:

 >>> import math >>> G.add_edge('y','x',function=math.cos) >>> G.add_node(math.cos) #    hashable    

आर्क को सरणियों और डेटा मानों से भी जोड़ा जा सकता है:

 >>> elist=[('a','b',5.0),('b','c',3.0),('a','c',1.0),('c','d',7.3)] >>> G.add_weighted_edges_from(elist) 

ग्राफ जानकारी प्राप्त करना

ग्राफ़ बनाने के अलावा, आपको आमतौर पर इसके नोड्स, आर्क्स, पाथ, आदि के बारे में जानकारी प्राप्त करने की आवश्यकता होती है। इसके लिए मुख्य तरीके नोड्स और आर्क्स (किनारों () और नोड्स) (), और साथ ही नोड्स और आर्क्स (किनारों_टर ()) पर एक इटरेटर प्राप्त करना है। और nodes_iter () क्रमशः।
इसके अतिरिक्त, ग्राफ़ के बारे में अधिक विशिष्ट जानकारी प्राप्त करने के लिए बड़ी संख्या में फ़ंक्शन हैं, उदाहरण के लिए, nx.triangles (G, n) ग्राफ़ G में त्रिकोणों की संख्या लौटाएगा जिसमें वर्टेक्स n नोड्स में से एक है।
सभी उपलब्ध फ़ंक्शन नेटवर्कएक्स में दस्तावेज़ अनुभाग में वर्णित हैं ।

पूर्वनिर्धारित एल्गोरिदम

पुस्तकालय ग्राफ पर काम करने के लिए विशिष्ट एल्गोरिदम की एक बड़ी संख्या को लागू करता है। अल्गोरिथम, सबसे छोटा रास्ता खोजने, ऊँचाई और चौड़ाई में खोज करने, क्लस्टरिंग, ग्राफ़ का समरूपता खोजना, और बहुत कुछ कार्यान्वित किया जाता है।
उदाहरण के लिए, एक भारित ग्राफ पर न्यूनतम पथ खोजने के लिए डेज्क्स्ट्रा का एल्गोरिदम निम्नानुसार लागू किया गया है:

 >>> G=nx.Graph() >>> e=[('a','b',0.3),('b','c',0.9),('a','c',0.5),('c','d',1.2)] >>> G.add_weighted_edges_from(e) >>> print(nx.dijkstra_path(G,'a','d')) ['a', 'c', 'd'] 

ग्राफ दृश्य

पुस्तकालय का मुख्य उद्देश्य रेखांकन के साथ काम करना है, और उनका दृश्य प्रदर्शन माध्यमिक है, लेकिन इसे लागू किया गया है, क्योंकि यह एक महत्वपूर्ण विश्लेषण उपकरण है।
अधिक जटिल मामलों के लिए मैटलपोटलिब पाइथन लाइब्रेरी या ग्राफविज़ प्लग-इन का उपयोग करके ग्राफ प्रदर्शित करने के लिए सुविधाजनक तरीके प्रदान किए जाते हैं। विज़ुअलाइज़ेशन क्षमताओं पर पूर्ण प्रलेखन networkx.lanl.gov/reference/drawing.html पर उपलब्ध है।
एक सरल ग्राफ दृश्य उदाहरण:

 >>> G=nx.cubical_graph() >>> nx.draw(G) #    spring_layout >>> nx.draw(G,pos=nx.spectral_layout(G), nodecolor='r',edge_color='b') 

Matplotlib का उपयोग करके विज़ुअलाइज़ेशन


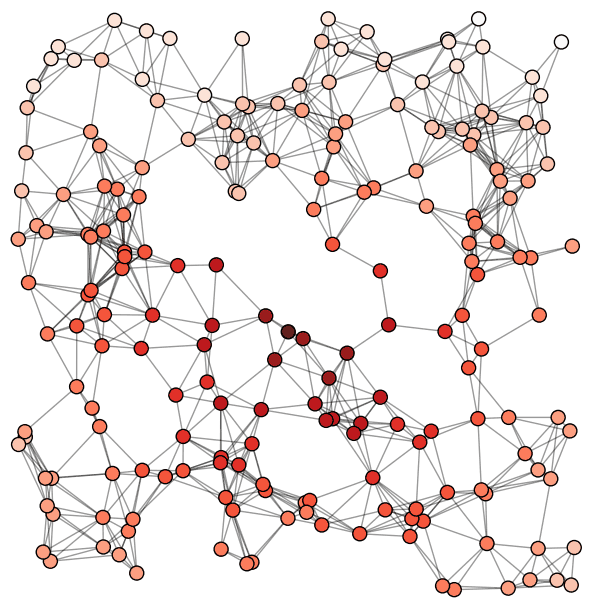
ग्राफविज़ का उपयोग करके विज़ुअलाइज़ेशन

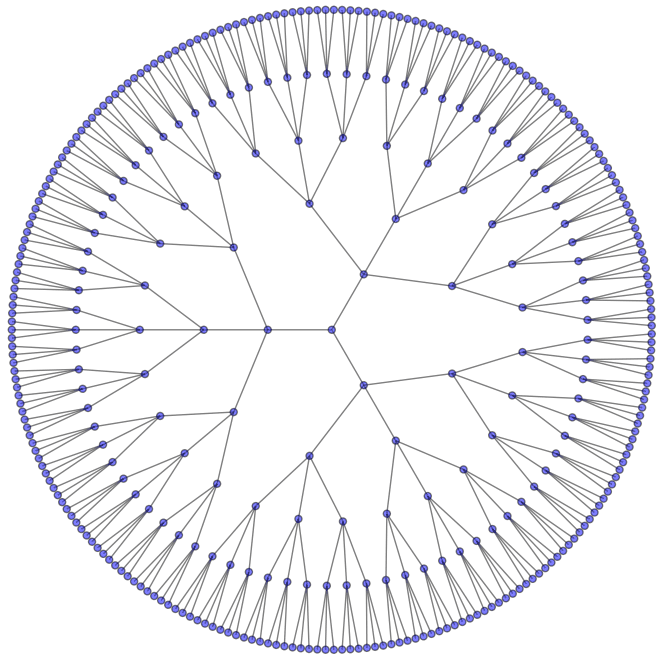
डेटा संरचनाएं

रेखांकन का संपूर्ण आंतरिक प्रतिनिधित्व मुख्य डेटा प्रकार के रूप में शब्दकोशों के शब्दकोश का उपयोग करता है। इस दृष्टिकोण के कई फायदे हैं। उदाहरण के लिए, एक बहुआयामी सरणी के तत्वों तक पहुंच का उपयोग करते हुए नोड्स के लिए सुविधाजनक पहुंच:

 >>> G=nx.Graph() >>> G.add_edge(1,2,color='red',weight=0.84,size=300) >>> print(G[1][2]['size']) 300 

अधिक विस्तृत प्रलेखन http://networkx.lanl.gov/reference/index पर स्थित है । एचटीएमएल
मुझे वास्तव में इस लाइब्रेरी के साथ काम करने में बहुत मज़ा आया। मैंने कुछ छोटी-छोटी लिपियों का इस्तेमाल किया और मुझे उम्मीद है कि मैं इसे एक छोटे अध्ययन में सफलतापूर्वक लागू करूँगा।
सफल परियोजनाएं!