कॉम्प्लेक्स प्लेन पर कोशा

इस वर्ष के वसंत दिनों में से एक, मैं ट्रॉली बस में सवार था और कोश के बारे में एक कॉमिक स्ट्रिप के माध्यम से पत्ती लगा रहा था। मुद्दों में से एक में वाक्यांश "लेकिन था! यह समझा जा सकता है, यह भग्न के साथ क्षितिज में बहता है , मुझे भी संकोच होगा ... " उसके बाद, मैंने खिड़की को देखा और महसूस किया कि यदि हम जटिल विमान a ( z ) और b ( z ) के दो उपयुक्त रैखिक भिन्नात्मक रूपांतरण लेते हैं, और a ( z ), b ( z ), a1 के लिए पुनरावृत्त कार्यों की प्रणाली पर विचार करते हैं। ( z ), b ( ¹ ( z ), प्रारंभिक सेट के रूप में कोश के साथ तस्वीर ले रहा है, फिर कोश क्षितिज में भग्न के साथ बहेगा!

और कुछ दिन पहले मेरे हाथ अजगर में आवश्यक स्क्रिप्ट लिखने के लिए पहुंचे। मेरे दोस्तों और मुझे परिणाम पसंद आए, और मैंने इस harastrastyu लिखने का फैसला किया।

इसलिए, यदि आप जानना चाहते हैं कि जटिल विमान के रैखिक-भिन्नात्मक रूपांतरण क्या हैं, और उन्हें भग्न छवियों को प्राप्त करने के लिए कैसे उपयोग करना है, तो हेब्रकट में आपका स्वागत है। थोड़ा बेकार गणित और कई जिफ होंगे।





तो, कोश K को लें और इसे जटिल तल पर रखें:



हम इसके साथ क्या कर सकते हैं? उदाहरण के लिए, हम किसी दिशा में आगे बढ़ सकते हैं। इस तरह के परिवर्तन को फॉर्म f ( z ) = z + a में लिखा जा सकता है, जहां एक जटिल संख्या है।



हम कोश को एक कोण पर घुमा सकते हैं। मूल के सापेक्ष। इस तरह के परिवर्तन को फॉर्म f ( z ) = e ⁱ can z में लिखा जा सकता है।



अंत में, हम कोष को उत्पत्ति के सापेक्ष कई गुना बढ़ा और ले सकते हैं। जैसा कि आप अनुमान लगा सकते हैं, ऐसे परिवर्तन को f ( z ) = kz लिखा जा सकता है।



किसी भी रैखिक जटिल परिवर्तन च ( z ) = a z + b को इन तीनों की रचना के रूप में दर्शाया जा सकता है।

अब हम कुछ परिवर्तन करें च ( z )। हम इस परिवर्तन की संरचना को अपने साथ लेते हैं, हम परिवर्तन च ( f ( z )) = f ² ( z ) प्राप्त करते हैं, फिर हम रचना f ( z ) और f ² ( z ) लेते हैं, हम परिवर्तन f ( f ² ( z )) = f प्राप्त करते हैं। f ( f ( z ))) = f ³ ( z ) और इसी तरह विज्ञापन infinitum पर। उदाहरण के लिए, यदि f ( z ) = z + a , तो f ⁿ ( z ) = z + na । हमारे कोश में परिवर्तनों की इस श्रृंखला को लागू करने और परिणाम के संयोजन से, हमें कुछ इस तरह मिलता है:



लेकिन, उदाहरण के लिए, यदि हम f ( z ) = k e ⁱ compression z (कोण k द्वारा गुणांक k प्लस घुमाव के साथ संपीड़न) लेते हैं, तो हमें एक और दिलचस्प तस्वीर मिलती है: कॉची से सर्पिल। (इस चित्र का निर्माण करते समय, मूल कोश को रखा गया था ताकि बिंदु 1 उसकी छाती पर, k = 0.8, π = φ / 3.)



मैं इस तथ्य पर ध्यान दूंगा कि सर्पिल को बिंदु 0 पर कर्ल किया गया है।

मानचित्र f ( z ) की सकारात्मक शक्तियों के साथ, हम शून्य और नकारात्मक लोगों पर विचार कर सकते हैं। शून्य के साथ, सब कुछ सरल है - यह पहचान मानचित्र है: f ⁰ ( z ) = id ( z ) = z नकारात्मक व्यक्ति थोड़े अधिक जटिल होते हैं: आपको पहले परिवर्तन च ( z ) को उल्टा करने की आवश्यकता है और फिर परिवर्तन positive1 ( z ) की सकारात्मक डिग्री पर विचार करें। पिछले पैराग्राफ से f ( z ) को बदलने के लिए f z1 ( z ) गुणांक 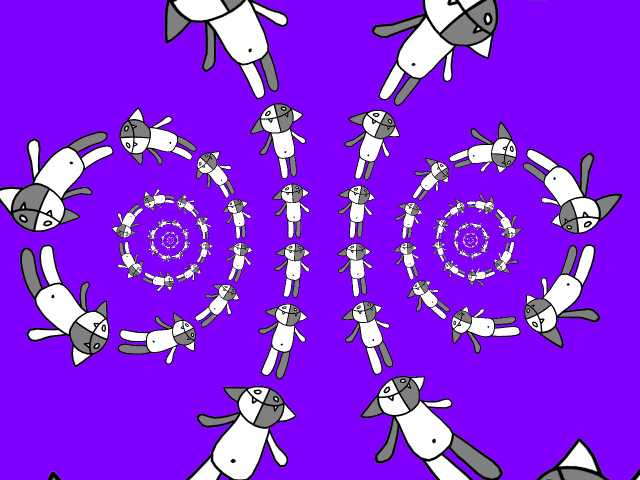k और एक घुमाव के साथ कोण a के साथ एक खिंचाव होगा। इसलिए, यदि परिवर्तन च (z) की सभी पूर्णांक शक्तियों द्वारा कोष पर कार्रवाई की जाती है और परिणाम संयुक्त होते हैं, तो हम कॉची के दोनों ओर एक अनंत सर्पिल प्राप्त करते हैं।



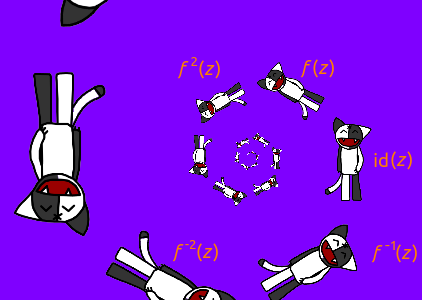
एक सर्पिल निश्चित रूप से अच्छा है, लेकिन आइए छवि को थोड़ा बढ़ाएं, इसके लिए हम ध्यान दें कि यदि इस सर्पिल में एफ ( जेड ) परिवर्तन लागू किया जाता है, तो कुछ भी नहीं बदलेगा। वास्तव में, कोई भी Cauchy f ⁿ ( K ) f ( f ⁿ ( K )) = f ^{n +1} ( K ) पर जाएगा, लेकिन वहाँ पहले से ही एक सर्पिल में ऐसा कोष है। और f ⁿ ( K ) कोश fn ( ¹ ( K ) गुजरता है। अगर हम N फ्रेम का gif बनाना चाहते हैं, तो हमें एक परिवर्तन g ( z ) के साथ आने की जरूरत है, जैसे कि g ^N ( z ) = f ( z )। लेकिन यह सरल है: g ( z ) = k ^{1 / N} e ^{i N / N} z, अर्थात, g ( z ) N समय को कम संपीड़ित करता है और f ( z ) की तुलना में N कोण को छोटा घुमाता है।



हम सर्पिल में लौट आएंगे, और अब कुछ भग्न हैं। सुविधा के लिए, हम निम्नलिखित संकेतन t _a ( z ) = z + a - shift by a , r _φ ( z ) - कोण φ द्वारा घूर्णन, और s _k ( z ) - कम्प्रेशन k समय का परिचय देते हैं। तीन परिवर्तनों पर विचार करें:

f ₁ ( z ) = t _i ( r ( _{/ 2} ( s _0,6 ( z ))),
f ₂ ( z ) = t _{sqrt (3) / 2 - 0.5 i} ( r ( _6/6 ( s _0.6 ( z )),)
f ₃ ( z ) = t _{qsqrt (3) / 2 - 0.5 i} ( r _{π5π / 6} ( s _0.6 ( z )))।

मान लीजिए कि उत्पत्ति कोश के केंद्र में है, तो परिवर्तन F ₁ ( z ) कोश के साथ क्या करता है? यह इसे लगभग दो बार संपीड़ित करता है, फिर इसे दाईं ओर रखता है और एक-एक करके ऊपर उठाता है। (मैं इस तथ्य पर आपका ध्यान आकर्षित करता हूं कि आपको परिवर्तनों को दाईं से बाईं ओर पढ़ने की आवश्यकता है।) अन्य दो रूपांतरण कुछ ऐसा ही करते हैं - इन परिवर्तनों को चुना जाता है ताकि कोष की छोटी प्रतियां नियमित त्रिभुज के कोने पर हों।



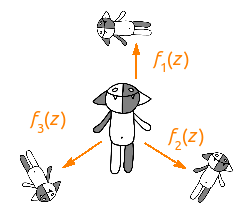
लेकिन हम तीन कॉची तक सीमित नहीं होना चाहते हैं, हमें उनमें से कई की आवश्यकता है, इसलिए हम परिवर्तनों की सभी प्रकार की रचनाओं पर विचार करेंगे f ₁ ( z ), f ₂ ( z ) और f ₃ ( z ): id ( z , f ₁ ( z ), f ₂ ( जेड ), एफ ₃ ( जेड ), एफ ₁ ( एफ ₁ ( जेड )), एफ ₁ ( एफ ₂ ( जेड )), एफ ₁ ( एफ ₃ ( जेड )), एफ ₂ ( एफ ₁ ( जेड )) , एफ ₂ ( एफ ₂ ( जेड )), एफ ₂ ( एफ ₃ ( जेड )), एफ ₃ ( एफ ₁ ( जेड )), एफ ₃ ( एफ ₂ ( जेड )), एफ ₃ ( एफ ₃ ( जेड )) , एफ ₁ ( एफ ₁ ( एफ ₁ ( जेड 2 ))), एफ ₁ ( एफ ₁ ( एफ ₂ ( जेड ))), ..., एफ ₃ ( एफ ₁ ( एफ ₂ ( एफ ₃ ( एफ ₁ ( जेड ))) )))), ... हम कोश पर परिवर्तनों के इस सेट के साथ कार्य करते हैं, और परिणामों को जोड़ते हैं। परिणाम अनुमानित है और नीचे दिया गया है।



एनिमेशन को फिर से जोड़ें, इस बार कोश की प्रतियां बनाने के लिए बड़े कोष के चारों ओर घूमें। इसे कैसे प्राप्त किया जाए? मान लें कि हम N फ्रेम बनाना चाहते हैं, फ्रेम k के लिए हम सही परिवर्तनों को मानते हैं f ₁ '( z ) = r 2 _{3k / (3N)} ( f ₁ ( z )), f ₂ ' ( z ) = r _{2πk / (3N)} ( f _{) 2} ( z ), f ₃ '( z ) = r _{2 /k / (3N)} ( f ₃ ( z ))। ये परिवर्तन मूल लोगों से भिन्न होते हैं कि वे कोष को एक नियमित त्रिभुज के कोने में स्थानांतरित करते हैं, जो मूल एक के सापेक्ष कोण 2 angle k / (3 N ) द्वारा घुमाया जाता है। परिणाम नीचे दिखाया गया है।



ऊपर दिए गए सभी रूपांतरण रैखिक थे, उनकी मदद से आप बहुत दिलचस्प नहीं कर सकते। परिवर्तन पर विचार करें: f ( z ) = 1 / z - वास्तविक अक्ष के सापेक्ष उलटा प्लस प्रतिबिंब। इस परिवर्तन से प्रभावित होने पर हमारे कोष का क्या होगा? यदि मूल कोष के अंदर नहीं है, तो यह ठीक है, कोश को पहले इकाई चक्र के संबंध में उलटा होना चाहिए, और फिर वास्तविक अक्ष के सापेक्ष फ़्लिप किया जाना चाहिए, और यदि 0 कोश के अंदर है, तो यह बस फट जाएगा (क्योंकि शून्य से विभाजित नहीं किया जा सकता है)। निम्नलिखित कुछ उदाहरण हैं।




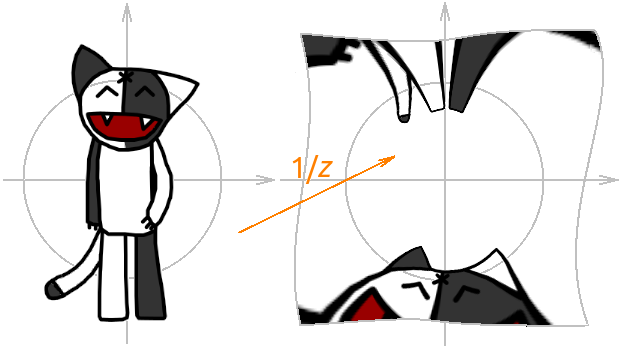
ध्यान दें कि 1 / z परिवर्तन इकाई वृत्त के बाहरी भाग को इकाई वृत्त के आंतरिक भाग में और इकाई वृत्त के बाहरी भाग को बाहरी में बदल देता है।

अब हम फॉर्म च ( z ) = ( az + b ) / ( cz + d ) के रूपांतरण पर विचार करते हैं। यह ऐसे परिवर्तन हैं जिन्हें रैखिक भिन्नात्मक कहा जाता है । इस तरह के किसी भी परिवर्तन को पहले से ज्ञात एक रचना के रूप में दर्शाया जा सकता है, जिसका नाम है: f ( z ) = f ₄ ( f ₃ ( f ₂ ( f ₁ ( z ))), जहाँ f ₁ ( z ) = z + d / c - पारी, f ₂ ( z ) = 1 / z - व्युत्क्रम प्लस परावर्तन, f3 ( z ) = - ( विज्ञापन - bc ) / c ² z - संपीडन / विस्तार + घूर्णन, f ₄ ( z ) = z + a / c - एक और बदलाव, इसलिए यदि किसी प्रकार का परिवर्तन किया जाता है, तो आप जल्दी से समझ सकते हैं कि यह क्या करता है।

अंश के रूप में परिवर्तन पर विचार करने की सुविधा इस प्रकार है: रैखिक-भिन्नात्मक परिवर्तनों की रचनाएँ खोजना और उन लोगों के लिए रेखीय-भिन्नात्मक परिवर्तनों को उलट देना बहुत ही सरल है जो मेट्रिसेस के साथ काम कर सकते हैं। वास्तव में, यदि एक परिवर्तन को 2 x 2 मैट्रिक्स दिया जाता है जिसमें गुणांक a , b , c , d स्पष्ट रूप से व्यवस्थित होते हैं, तो रचना मैट्रिक्स के उत्पाद से मेल खाती है, और व्युत्क्रम मैट्रिक्स के व्युत्क्रम से मेल खाती है।

दूसरी सुविधा यह है कि रिकॉर्ड से तुरंत आप देख सकते हैं कि बिंदु 0 किस बिंदु पर जाता है, और कौन सा बिंदु अनंत जाता है, और यह भी कि कौन सा बिंदु 0 पर जाता है और कौन सा अनंत तक जाता है।

हमारे लिए एक और महत्वपूर्ण संपत्ति यह तथ्य है कि लाइनें लाइनों या सर्कल में जाती हैं, और सर्कल भी या तो लाइनों में या सर्कल में होती हैं। अधिक सटीक रूप से: यदि एक रेखा या वृत्त में एक बिंदु होता है जो अनंत तक जाता है, तो यह एक रेखा बन जाएगी, अन्यथा यह एक चक्र बन जाएगा।

आइए अपने सर्पिल पर वापस जाएं। हम इस पर एक परिवर्तन लागू करते हैं, जो 0 and1 में अनुवाद करता है, और अनंत - 1: r ( z ) = ( z + 1) / ( z - 1) में। चूंकि सर्पिल शून्य के आसपास घाव था, अब यह लगभग but1 के आसपास घाव होना शुरू हो जाएगा, लेकिन यह भी कि सर्पिल अनंत से निराधार था, इसलिए यह 1 से निराधार होगा।



कॉम्प्लेक्स प्लेन पर पोलर ग्रिड पर विचार करें और इस ग्रिड के प्रत्येक सेल में कोश रखें।



परिवर्तन च ( z ) = k e ⁱ । Z पर विचार करें । यह एक कोण compress द्वारा ध्रुवीय ग्रिड को घुमाता है और सभी कोशिकाओं को कई बार संकुचित करता है। यदि हम उत्तराधिकार में कई फ्रेमों पर विचार करते हैं, तो हमें निम्नलिखित मिलते हैं:



यदि हम किसी भी कॉची पर नज़र रखने की कोशिश करते हैं, तो हम देखेंगे कि यह एक घुमावदार सर्पिल के साथ चलती है, और हमने पहले ही इसका पता लगा लिया है, इसलिए यह स्पष्ट है कि यदि हम अभी भी परिवर्तन r ( z ) = ( z 1) 1 (/) करेंगे z - 1)।



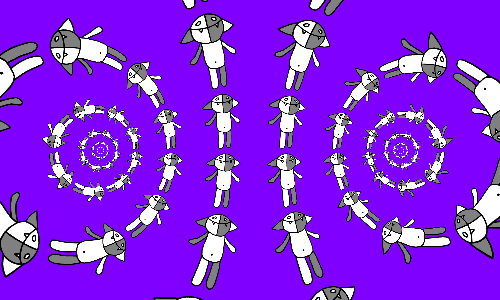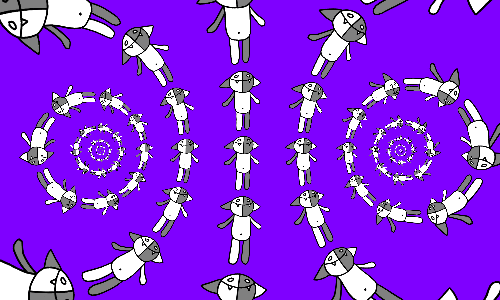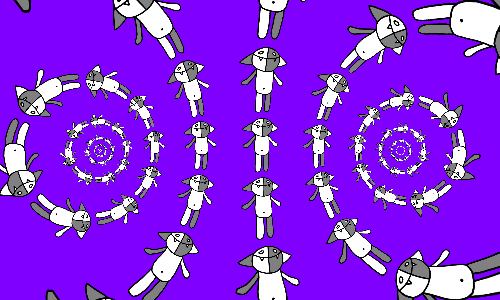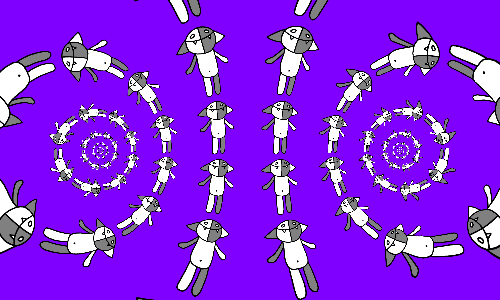
यदि मेष के प्रत्येक कोशिका में कोष अपनी तरफ रखा जाता है, तो हमें थोड़ा अलग चित्र मिलता है।



परिवर्तन च ( z ) लॉक्सोड्रोमिक है, कोई अन्य प्रकार के परिवर्तनों पर भी विचार कर सकता है।

हमने एक रेखीय अंश परिवर्तन का पता लगाया, अब आपको अपने आप को स्वादिष्ट चाय का एक कप डालना चाहिए और दो परिवर्तनों पर विचार करना चाहिए:

a ( z ) = (sqrt (2) z + 1) / ( z + sqrt (2)),
b ( z ) = (sqrt (2) z + i ) / (- iz + sqrt (2))।

( Z ) रूपांतरण क्या करता है? हम इसे रचना f ₄ ( f ₃ ( f ₂ ( f ₁ ( z ))): f ₁ ( z ) = z + sqrt (2) - sqrt (2) को दाईं ओर फेरस करते हैं। F ₂ ( z ) = 1 / z में विघटित करते हैं। z - मूल के विपरीत व्युत्क्रम, और वास्तविक धुरी के सापेक्ष प्रतिबिंब, f ₃ ( z ) = - z - कोण के माध्यम से रोटेशन to, f ₄ ( z ) = z + sqrt (2) - दाईं ओर sqrt (2) में स्थानांतरित करें। सभी एक साथ, यह पता चला है कि itsqrt (2) में केंद्र के साथ इकाई सर्कल C ₁ का बाहरी वर्ग sqrt (2) में केंद्र के साथ इकाई सर्कल C ₂ के आंतरिक भाग में जाता है, और सर्कल C ₂ के बाहरी भाग में सर्कल ₁ के अंदर होता है ।

परिवर्तन ^should1 ( z ) कार्य करता है, क्योंकि यह उलटा परिवर्तन होना चाहिए, बिल्कुल विपरीत।

B ( z ) परिवर्तन एक समान तरीके से काम करता है - केवल सर्कल C ₁ और C ₂ के बिंदुओं पर केंद्र हैं - i sqrt (2) और sqrt (2)।



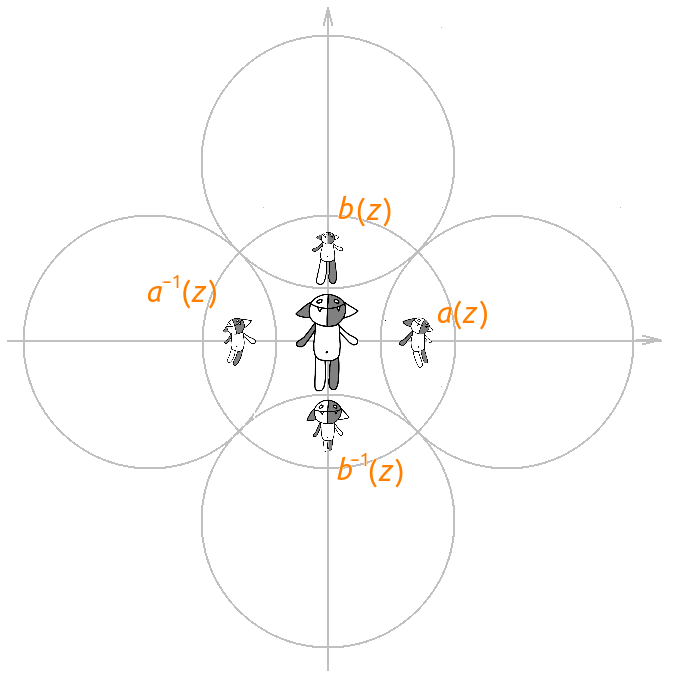
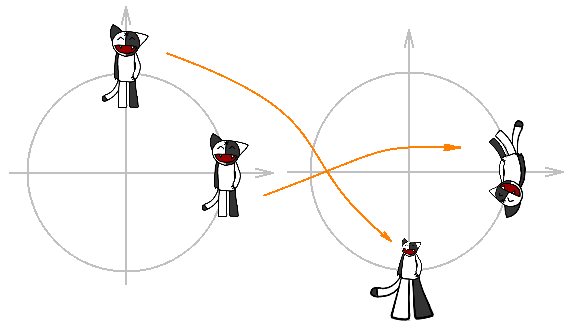
यह भग्न में आगे बढ़ने का समय है: नक्शे की सभी प्रकार की रचनाओं पर विचार करें a ( z ), b ( z ), ) ¹ ( z ) और b ( ¹ ( z ) और कोष पर उन पर कार्य करें:



जीआईएफ प्राप्त करने के लिए, फिर से ध्यान दें कि यदि हम परिणामस्वरूप तस्वीर में ए ( जेड ) या बी ( जेड ) लागू करते हैं, तो कुछ भी नहीं बदलेगा। उदाहरण के लिए, b (z) पर विचार करें: हम एक परिवर्तन g ( z ) के साथ आते हैं, जैसे कि G ^N ( z ) = b ( z )। यह करना मुश्किल नहीं है, क्योंकि यह ज्ञात है कि परिवर्तन b ( z ) को b ( z ) = t ( ¹ ( m ( t ( z ))) के रूप में दर्शाया जा सकता है, जहाँ t ( z ) = ( z - z ₁ ) / ( z - z ₂ ), m ( z ) = k e ⁱ and z , और z ₁ और z ₂ मानचित्र b ( z ) के निश्चित बिंदु हैं।
निश्चित अंक खोजना मुश्किल नहीं है: हम द्विघात समीकरण को हल करते हैं b ( z ) = z और get z ₁ = - i , z ₂ = i , whence हमें मिलता है कि m ( z ) = t ( a ( t ( ¹ ( z ))), इसलिए , m ( z ) = (sqrt (2) + 1) z / (sqrt (2) - 1)। इसलिए, g ( z ) = t ( ¹ ((sqrt (2) + 1) ^{1 / N} t ( z ) / (sqrt (2) - 1) ^{1 / N} ) = (( q + w ) z / 2 + i ( q - w ) / 2) / (- i ( q - w ) z / 2 + ( q + w ) / 2)), जहाँ q = (sqrt (2) + 1) ^{1 / N} , w = (sqrt) (२) - १) ^{१ / एन।}

हम कार्यक्रम और प्राप्त करते हैं:



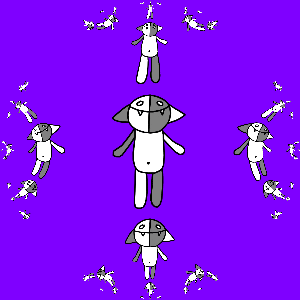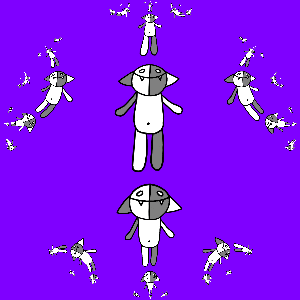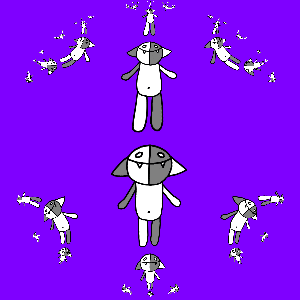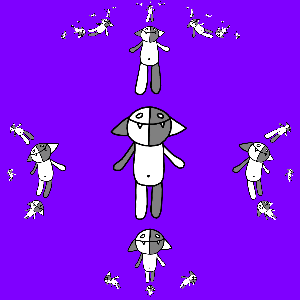
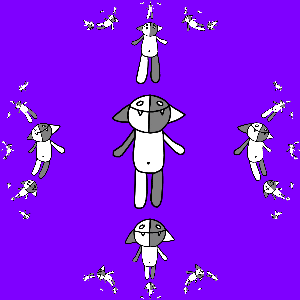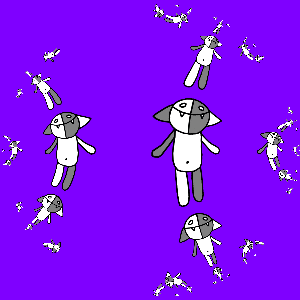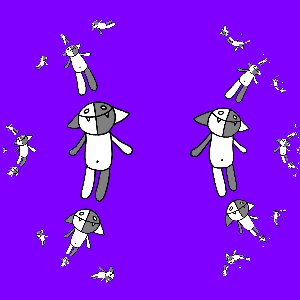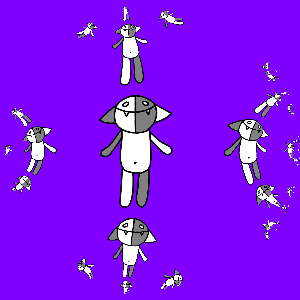
यहां यह ध्यान रखना दिलचस्प है कि ट्रांसफ़ॉर्मेशन जी ( z ) यूनिट डिस्क का ऑटोमोरिज़्म साबित हुआ।

अंत में, यदि हम पहले कॉची, और फिर शेष मैपिंग के लिए जी ( जेड ) लागू करते हैं, तो यह काफी अच्छी तरह से निकल जाएगा:



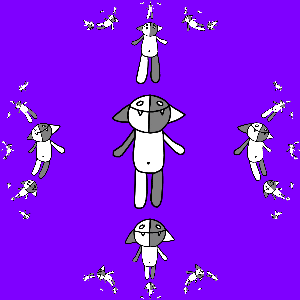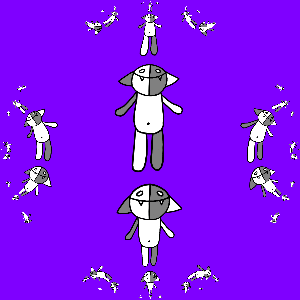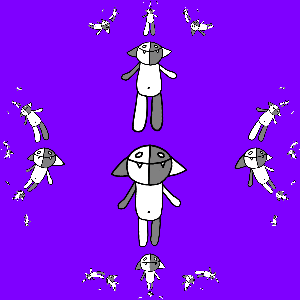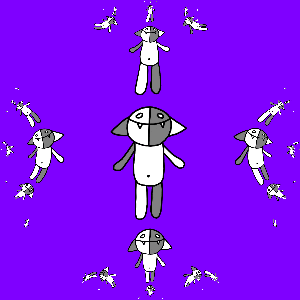
वह सब है।

अगर कोई और जानना चाहता है, तो मैं इंद्र के मोती ममफोर्ड और अन्य लोगों को सलाह देता हूं।

अगर कोई प्रयोग करना चाहता है, तो कोड को जीथब पर रखा जाता है।

यदि कोई क्रॉल करना चाहता है, तो आप इसे कूप पर कर सकते हैं: एक और दो ।