छवि विभाजन

छवि विभाजन

छवि प्रसंस्करण और विश्लेषण के मुख्य कार्यों में से एक है विभाजन, अर्थात्। छवि को उन क्षेत्रों में विभाजित करना जिनके लिए एक निश्चित एकरूपता मानदंड पूरा होता है, उदाहरण के लिए, छवि पर लगभग समान चमक के क्षेत्रों को उजागर करना। छवि क्षेत्र की अवधारणा का उपयोग एक निश्चित सामान्य विशेषता (संपत्ति) वाले छवि तत्वों के जुड़े समूह को निर्धारित करने के लिए किया जाता है।
मुख्य और सरल तरीकों में से एक एक सीमा का उपयोग करके एक विभाजन बनाना है। दहलीज एक संकेत (संपत्ति) है जो वांछित संकेत को कक्षाओं में विभाजित करने में मदद करता है। थ्रेशोल्ड पृथक्करण का संचालन छवि में प्रत्येक पिक्सेल के चमक मान की निर्दिष्ट थ्रेशोल्ड मान से तुलना करना है।

binarization

थ्रेशोल्ड पृथक्करण का संचालन, जिसके परिणामस्वरूप एक द्विआधारी छवि होती है, को बिनारीकरण कहा जाता है। बिनाराइजेशन ऑपरेशन का उद्देश्य छवि में निहित जानकारी की मात्रा को काफी कम करना है। बाइनराइजेशन की प्रक्रिया में, प्रारंभिक ग्रेस्केल छवि, जिसमें एक निश्चित संख्या में चमक का स्तर होता है, एक काले और सफेद छवि में परिवर्तित हो जाती है, जिसके पिक्सल में केवल दो मान होते हैं - 0 और 1

थ्रेसहोल्ड इमेज प्रोसेसिंग को विभिन्न तरीकों से किया जा सकता है।

एक कम दहलीज के साथ द्विभाजन

एक कम दहलीज के साथ द्विभाजन
निचली सीमा के साथ द्विभाजन सबसे सरल ऑपरेशन है, जिसमें केवल एक सीमा मूल्य का उपयोग किया जाता है:

मानदंड के बजाय सभी मान 1 हो जाते हैं, इस मामले में 255 (सफेद) और पिक्सेल के सभी मूल्य (आयाम) जो कि थ्रेशोल्ड टी 0 से अधिक हैं (काला)।

ऊपरी थ्रेशोल्ड बिनारिएशन
कभी-कभी आप पहले तरीके के एक संस्करण का उपयोग कर सकते हैं, जो कि द्विप्रकरण प्रक्रिया में प्राप्त नकारात्मक छवि देता है। ऊपरी थ्रेशोल्ड के साथ बिनाराइजेशन ऑपरेशन:


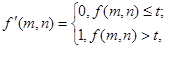डबल लिमिट बिनराइजेशन
उन क्षेत्रों को उजागर करने के लिए जिनमें पिक्सेल चमक मान एक ज्ञात सीमा में भिन्न हो सकते हैं, द्वैरीकरण को दोहरे प्रतिबंध (टी ₁ <टी ₂ ) के साथ पेश किया गया है:

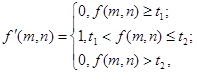
थ्रेसहोल्ड के साथ अन्य विविधताएं भी संभव हैं, जहां डेटा का केवल एक हिस्सा छोड़ दिया जाता है (मध्य-पास फ़िल्टर)।

अपूर्ण थ्रेशोल्ड प्रसंस्करण
यह रूपांतरण एक छवि देता है जो आगे के विश्लेषण के लिए आसान हो सकता है, क्योंकि यह मूल छवि में मौजूद सभी विवरणों के साथ पृष्ठभूमि से रहित हो जाता है।

बहुस्तरीय थ्रेसहोल्ड रूपांतरण
यह ऑपरेशन एक छवि उत्पन्न करता है जो बाइनरी नहीं है, लेकिन विभिन्न चमक वाले खंडों से मिलकर बनता है।


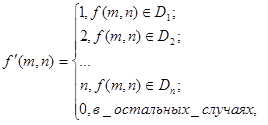
बिनाराइजेशन के लिए, यह मूल रूप से है। यद्यपि आप यह जोड़ सकते हैं कि एक वैश्विक एक है जो पूरी छवि के लिए उपयोग किया जाता है और एक स्थानीय भी है जो चित्र (छवि) के हिस्से को कैप्चर करता है।

स्थानीय थ्रेशोल्ड प्रसंस्करण

ओट्स विधि
विधि एक रास्टर छवि के पिक्सेल चमक मूल्यों के वितरण के एक हिस्टोग्राम का उपयोग करती है। एक हिस्टोग्राम का निर्माण p _i = n _i / N के मान से किया जाता है, जहाँ N छवि में पिक्सेल की कुल संख्या है, n _i चमक स्तर के साथ पिक्सेल की संख्या है। ब्राइटनेस रेंज को दो वर्गों में विभाजित किया जाता है, जो ब्राइटनेस लेवल k की थ्रेशोल्ड वैल्यू का उपयोग करता है, k 0 से लेकर L तक का एक पूर्णांक मान है। प्रत्येक वर्ग सापेक्ष आवृत्तियों से मेल खाता है L ₀ : ₁ :

दो छवि वर्गों में से प्रत्येक के लिए औसत स्तर:
अगला, छवि अलगाव की गुणवत्ता को दो भागों में आंकने के लिए अधिकतम मूल्य की गणना की जाती है:
जहां ( _ωcl ) 2 = ω ₀ μ ₁ (μ ₁ -μ ₀ ) ² , इंटरक्लास फैलाव है, और () _कुल ) ² पूरी छवि के लिए कुल फैलाव है।

छवि चमक ढाल के आधार पर थ्रेशोल्ड निर्धारण
मान लीजिए कि विश्लेषण की गई छवि को दो वर्गों - वस्तुओं और पृष्ठभूमि में विभाजित किया जा सकता है। दहलीज गणना एल्गोरिथ्म में निम्नलिखित 2 चरण होते हैं:
1. प्रत्येक पिक्सेल के लिए चमक ढाल का मापांक निर्धारित किया जाता है
छवि

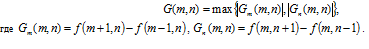
2. दहलीज की गणना:


हिस्टोग्राम के एन्ट्रॉपी का उपयोग करने की विधि
विधि ने इसके विभिन्न रूपों और संभावित विविधताओं को हासिल कर लिया है। विभिन्न कानूनों और वितरण के रूपों का उपयोग करके एक निश्चित राशि से थ्रेसहोल्ड के कुल द्रव्यमान का वितरण।

वैश्विक थ्रेशोल्ड प्रसंस्करण

बर्नसन विधि
1. विषम संख्या में पिक्सेल के साथ एक साधारण वर्ग एपर्चर मूल छवि के सभी पिक्सेल के माध्यम से एक चक्र में चलता है। हर कदम मिन और मैक्स है।
2. औसत मान औसत = (न्यूनतम + अधिकतम) / 2 पाया जाता है।
3. यदि वर्तमान पिक्सेल औसत <E से बड़ा है - तो यह सफेद हो जाता है, अन्यथा - काला। ई - उपयोगकर्ता द्वारा निर्दिष्ट एक निश्चित निरंतर।
4. यदि औसत विपरीत सीमा से कम है, तो वर्तमान पिक्सेल "संदिग्ध पिक्सेल के रंग" पैरामीटर द्वारा निर्दिष्ट रंग बन जाता है।
इसके कई नुकसान हैं: नीरस चमक वाले क्षेत्रों को संसाधित करने के बाद, मजबूत संयम हस्तक्षेप का गठन होता है, कुछ मामलों में यह झूठे काले धब्बे की उपस्थिति की ओर जाता है
आकिल की विधि
सबसे उत्पादक विधियों में से एक ईकवल विधि है। इसका उपयोग अक्सर स्पष्ट और विषम छवियों के प्रसंस्करण के लिए किया जाता है। इस पद्धति के अनुसार, छवि को दो संकेंद्रित खिड़कियों का उपयोग करके संसाधित किया जाता है: छोटे - एस, और बड़े एल। आमतौर पर, खिड़कियों का आकार चौकोर माना जाता है। दोनों विंडो छोटी से छोटी विंडो एस के किनारे के बराबर वेतन वृद्धि की छवि में बाएं से दाएं ऊपर से नीचे तक सुपरिंपोज की जाती हैं। विंडो एल के लिए, थ्रेसहोल्ड बी की गणना की जाती है ताकि पिक्सल दो समूहों में विभाजित हो। यदि दो समूहों में चमक स्तर की गणितीय अपेक्षाओं में कुछ उपयोगकर्ता-परिभाषित स्तर / μ ₁ -μ ₂ / alll से अधिक का अंतर होता है, तो विंडो S के अंदर के सभी पिक्सेल थ्रेशोल्ड T के अनुसार बायनेरीज़ होते हैं। अन्यथा, विंडो S से पिक्सेल की चमक को कुछ से बदल दिया जाता है। करीब मूल्य।
निबलैक विधि
इस विधि का विचार स्थानीय मानक विचलन के आधार पर बिंदु से बिंदु तक द्विभाजन की चमक दहलीज बी को अलग करना है। बिंदु पर चमक सीमा (x, y) की गणना निम्नानुसार की जाती है:

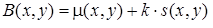
जहाँ μ (x, y) माध्य और s (x, y) बिंदु के कुछ पड़ोस के लिए नमूने का मानक विचलन है। पड़ोस का आकार न्यूनतम होना चाहिए, लेकिन जैसे कि छवि के स्थानीय विवरणों को संरक्षित करने के लिए। इसी समय, परिणाम पर शोर के प्रभाव को कम करने के लिए आकार काफी बड़ा होना चाहिए। K का मान यह निर्धारित करता है कि वस्तु की सीमा का कौन सा भाग खुद वस्तु के रूप में लेना है। K = -0.2 का मान वस्तुओं के काफी अच्छे पृथक्करण को परिभाषित करता है यदि वे काले रंग में प्रस्तुत किए जाते हैं, और k = + 0.2 का मान, यदि वस्तुओं को सफेद रंग में दर्शाया जाता है।
द जेनोवित्ज़ और ब्रुकस्टीन विधि
चमक ढाल के स्थानीय अधिकतमकरण के आधार पर संभावित सतह का उपयोग बिनाराइजेशन की दहलीज सतह के रूप में किया जाता है। ल्यूमिनेंस ढाल की शुरुआत की गणना अक्सर सोबेल या कैनी लूप ऑपरेटर के उपयोग से की जाती है। 1 पिक्सेल की मोटाई के साथ समोच्च लाइनें प्राप्त करने के लिए छवि को फ़िल्टर्ड किया जाता है, और फिर एक 3 × 3 औसत फ़िल्टर। संभावित सतह, अब, एक पुनरावृत्त प्रक्षेप योजना के अनुसार निर्मित है। सतह की गणना क्रम में है, जो रूपरेखा पिक्सल से शुरू होती है। प्रत्येक गैर-समोच्च पिक्सेल के लिए, प्रक्षेप अवशेषों R (x, y) की गणना की जाती है और चरण n + 1 पर नए पिक्सेल मान P (x, y) को सूत्रों के अनुसार गणना की जानी चाहिए:

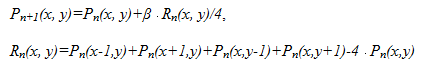
β तेजी से अभिसरण के लिए 1β2 के भीतर।

कुल मिलाकर

मैंने इसे खुशी के साथ पाया जो मैंने भविष्य में आपके लिए रखा है, अगर यह काम करता है और समय होगा, तो मैं कुछ एल्गोरिदम को लागू करने का प्रयास करूंगा। यह आज मौजूद हर चीज का एक छोटा सा हिस्सा है, लेकिन मुझे यह साझा करने में खुशी है।
आपका ध्यान देने के लिए धन्यवाद।