परिचय
 Bo_bda
Bo_bda का एक सहकर्मी छवि प्रसंस्करण और विश्लेषण की मूलभूत समस्याओं के बारे में बात करता है। खैर, मैं पक्ष में नहीं रह सकता और अपना अनुभव साझा नहीं कर सकता। आज मैं आपको मार्कोव नेटवर्क (विदेशी साहित्य में मार्कोव यादृच्छिक क्षेत्रों) के रूप में एक ऐसी दिलचस्प बात के बारे में बताऊंगा। इस गणितीय मॉडल का उपयोग ग्राफिक्स प्रसंस्करण के लगभग सभी कार्यों को हल करने के लिए किया जाता है (यहां आपके पास विभाजन, छवि बहाली, स्टीरियो इमेजिंग, 3 डी में विभिन्न प्रश्न और बहुत कुछ है)।
चेतावनी! चित्रों के कट टन के तहत (ग्राफिक्स के बारे में ब्लॉग पोस्ट वह है जो इसके लिए होगा)।
समस्या का बयान

एक नियम के रूप में, 2 प्रकार के कार्य हैं: प्रत्यक्ष और व्युत्क्रम। उदाहरण के लिए, एक प्रत्यक्ष कार्य अक्सर कंप्यूटर ग्राफिक्स में हल किया जाता है: हम प्रकाश स्रोतों, इनपुट के पर्यावरणीय मापदंडों का एक सेट देते हैं, और हमें आउटपुट पर एक दृश्य मॉडल मिलता है। कंप्यूटर दृष्टि में, सब कुछ सटीक है, लेकिन इसके विपरीत - हम यह पता लगाने के लिए छवियों का एक सेट फ़ीड करते हैं कि वे चीज़ में कहां रुचि रखते हैं (मशीन सीखने में, एक बहुत ही समान अर्थ -
प्रतिगमन के साथ एक अवधारणा है)। औपचारिक रूप से, समस्या को निम्नानुसार परिभाषित किया जा सकता है: दिए गए मानों के लिए, हमारे लिए अज्ञात कुछ मॉडल के मापदंडों की गणना करना आवश्यक है।
बारीकियों के लिए, आइए निम्न समस्या को हल करने का प्रयास करें: हम ऊपर दिए गए चित्र में स्टारफ़िश का चयन करते हैं, बशर्ते कि हम उस वस्तु को चिह्नित कर सकें जिसकी हमें ज़रूरत है (लाल स्ट्रोक) और बाकी सब (क्रमशः नीला)।
सैद्धांतिक पृष्ठभूमि
इसलिए, स्ट्रोक के साथ हमने एक निश्चित स्थिति को संतुष्ट करने वाले बिंदुओं का एक मनमाना सेट चिह्नित किया।
सांख्यिकीय निष्कर्ष को उसके भाग (
विकी ) के आधार पर पूरे नमूने के बारे में जानकारी प्राप्त करना कहा जाता है। 2 मुख्य दृष्टिकोण हैं - आवृत्ति और बायेसियन। हम बाद का उपयोग करेंगे, क्योंकि यह हमारे लिए एक बहुत ही रोचक और उपयोगी अवधारणा द्वारा संचालित है - एक प्राथमिकता संभावना।
पी
के एक निश्चित मूल्य का
एक प्राथमिकता संभावना वितरण एक संभावना वितरण है जो खाता प्रयोगात्मक डेटा (
विकी ) में लेने से पहले पी के बारे में मान्यताओं को व्यक्त करता है। क्या यह नहीं पता कि हमारी स्थितियों के लिए बहुत उपयुक्त है? :)
गणितीय आंकड़ों में
संभावना फ़ंक्शन पैरामीट्रिक वितरण से एक नमूना का संयुक्त वितरण है, जिसे एक पैरामीटर फ़ंक्शन (
विकी ) माना जाता है।
पोस्टीरियर मैक्सिमम (अधिकतम एक पोस्टवर्दी - एमएपी) का
अनुमान लगाना, आपको एक प्राथमिकता मूल्य वितरण (
विकी ) का उपयोग करके एक निश्चित मूल्य की गणना करने की अनुमति देता है।
बिंदु पर पहुँचो
हम जिस परिवर्तन की तलाश कर रहे हैं उसे निम्नानुसार वर्णित किया जा सकता है:
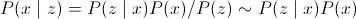
जहाँ
पी (x | z) - पश्चगामी संभावना (
विकी );
पी (z | x) संभावना फ़ंक्शन है (यह डेटा पर निर्भर करता है, अर्थात वर्तमान छवि);
P (x) - एक प्रायोरिटी प्रायिकता (डेटा पर निर्भर नहीं करता है)।
वास्तव में, सबसे अच्छा अलगाव खोजने की समस्या निम्नानुसार बनाई जा सकती है:
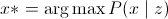
(यह सूत्र है और MAP को व्यक्त करता है), या, जो समान है

जहाँ
ई (एक्स) - छवि ऊर्जा।
प्रत्येक भाग पर अलग से विचार करें।
संभावना समारोह

X = 0 या x = 1 पर यह फ़ंक्शन दिखाता है कि क्या वर्तमान पिक्सेल z छवि के वांछित क्षेत्र से संबंधित है। दाईं ओर की आकृति में आप इसे देख सकते हैं।
परिणाम को बेहतर बनाने के लिए, हमें अधिकतम खोजने की आवश्यकता है:

परिणाम निम्न होना चाहिए:

पूर्व संभावना
यह पैरामीटर आपको सेगमेंट करते समय पड़ोसी पिक्सेल को ध्यान में रखने की अनुमति देता है। वर्तमान पिक्सेल को अपने पड़ोसियों के साथ लंबवत और क्षैतिज रूप से कनेक्ट करें। तब:
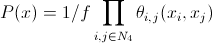
जहाँ
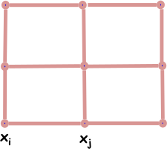
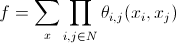
- जुदाई समारोह;
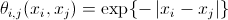
- "ईज़िंग पूर्व" (
युरिव के संकेत पर
ईज़िंग की एक पूर्व संभावना)।
इस मामले में, सभी को
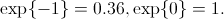
बाद की संभावना
इस शब्द को निर्धारित करने में, हम गिब्स वितरण (
विकी ) का उपयोग करते हैं:

जहाँ

- छवि की ऊर्जा, जहां पहला शब्द अपने आप में वर्तमान पिक्सेल का ऊर्जा मूल्य है, और दूसरा पड़ोसी के साथ कुल मूल्य है; डब्ल्यू एक निश्चित वजन है, जिसका मूल्य प्रयोगात्मक रूप से निर्धारित किया जाता है;

- संभावना समारोह;
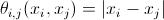
- एक प्राथमिकता संभावना।
काहे, बस थोड़ा सा अवशेष, सबसे महत्वपूर्ण बात।
ऊर्जा कम से कम
जैसा कि हमने शुरुआत में स्थापित किया था, न्यूनतम ऊर्जा एमएपी से मेल खाती है। इस मामले में:
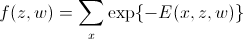
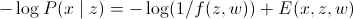

(न्यूनतम ऊर्जा की मांग)

परिणाम
"यह क्या था और, सबसे महत्वपूर्ण बात, क्यों?", पाठक पूछेगा। यहाँ आप के साथ अंत कर सकते हैं, वजन w के विभिन्न मूल्यों का संकेत:
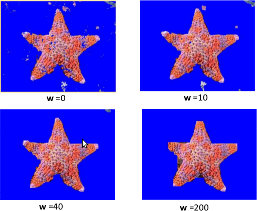
निष्कर्ष
इस पद्धति का विशेष आकर्षण यह है कि हम कोई भी ऊर्जा सूत्र निर्धारित कर सकते हैं। उदाहरण के लिए, आप विशेष रूप से सीधी रेखाओं की छवि पर चयन प्राप्त कर सकते हैं, एक निश्चित संख्या में रेखाओं / वक्रों के प्रतिच्छेदन बिंदु और बहुत कुछ। वैसे, एमएस ऑफिस 2010 का कोई भी भाग्यशाली मालिक वर्णित तकनीक को महसूस कर सकता है। बस बैकग्राउंड रिमूवल टूल का उपयोग करें।
आपका ध्यान के लिए धन्यवाद!
कॉपीराइटर कॉर्नर
उपयोग की जाने वाली सभी छवियां कार्स्टन रोदर से हैं। सूत्र ऑनलाइन
लेटेक्स दुभाषिया का उपयोग करके बनाए गए हैं।
गंभीर साहित्य की सूची
- कार्स्टन रॉदर काम करता है
- पुस्तक रिचर्ड सेज़िस्की कंप्यूटर विजन: एल्गोरिदम और अनुप्रयोग