कतरन एल्गोरिदम

कंप्यूटर की शक्ति में वृद्धि के साथ, अधिक से अधिक लोग ग्राफिक्स के साथ काम करने की कोशिश कर रहे हैं। पहली नज़र में, कई एल्गोरिदम सहज ज्ञान युक्त लगते हैं, लेकिन यदि आप चाहते हैं कि आपका आवेदन स्वीकार्य गति से काम करे, तो आपको शास्त्रीय एल्गोरिदम का अध्ययन करना होगा।

यह पद एक ही कार्य के उद्देश्य से कई एल्गोरिदम के विश्लेषण के लिए समर्पित है, जो खंडों को काटने का कार्य करता है। छवियों को बनाते समय, मनमाने आकार और आकार के आकार प्राप्त किए जा सकते हैं। अक्सर मॉनिटर पूरे उत्पन्न छवि को प्रदर्शित नहीं कर सकता है। इसके अलावा, कभी-कभी ऐसी परिस्थितियां होती हैं जब स्क्रीन पर छवि के क्षेत्र को सेट करना आवश्यक होता है और केवल इस क्षेत्र के अंदर छवियों को प्रदर्शित करता है। इन समस्याओं को हल करने के लिए, कतरन एल्गोरिदम का आविष्कार किया गया था।

खंडों को काटना

सबसे सरल क्लिपिंग कार्य खंडों को काटना है। हम इसे एक ठोस उदाहरण पर तैयार करते हैं। हम मानते हैं कि आउटपुट क्षेत्र को आयत ABCD द्वारा परिभाषित किया गया है। एक उदाहरण पर विचार करें, और कट-ऑफ फिगर के रूप में त्रिकोण PRQ को लें।



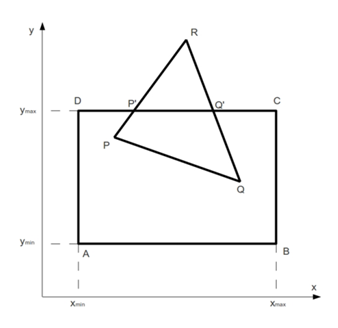
कतरन प्रक्रिया पूरी तरह से स्वचालित होनी चाहिए। यानी PRQ त्रिकोण को आकर्षित करने के लिए, केवल PQ; PP '; Q' Q लाइन ड्राइंग कमांड्स को निष्पादित किया जाना चाहिए। इसके अलावा, बिंदु P 'के निर्देशांक; Q' पहले से ज्ञात नहीं हैं।
व्यवहार में, खंड और आउटपुट क्षेत्र के बिंदुओं के सापेक्ष स्थानों की एक बड़ी संख्या संभव है। यह विविधता एल्गोरिथ्म के दृष्टिकोण से क्लिपिंग ऑपरेशन को अत्यधिक सहज बनाती है। इन समस्याओं को हल करने के लिए, कतरन एल्गोरिदम बनाया गया है।

सदरलैंड-कोहेन एल्गोरिथम

सदरलैंड और कोहेन द्वारा प्रस्तावित कतरन एल्गोरिथ्म बहुत दिलचस्प है। एल्गोरिथ्म का सार यह है कि एक चार-बिट कोड खंड के सिरों को सौंपा गया है: बी ₀ , बी ₁ , बी ₂ , बी ₃ । इस चार-बिट कोड में आउटपुट क्षेत्र के सापेक्ष बिंदु की स्थिति के बारे में जानकारी होती है। व्यवहार में, 9 संयोजन संभव हैं:

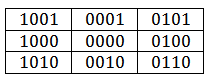
ये कोड बताएं:
ये कोड बताएं:

• बी ₀ = 0 यदि x≥x _मिनट ;
• b ₀ = 1 यदि x <x _मिनट ;
• बी ₁ = 0 यदि x≤x _{अधिकतम} ;
• b ₁ = 1 यदि x> x _{अधिकतम} ;
• b ₂ = 0 यदि y≥y _min ;
• b ₂ = 1 यदि y <y _मिनट ;
• b ₃ = 0 यदि _{अधिकतम हो} ;
• b ₃ = 1 यदि y> y _{अधिकतम} ;

कोड प्राप्त होने के बाद, निम्नलिखित विकल्प संभव हैं:

1. कोड में केवल 0 होते हैं, जिसका अर्थ है कि पूरा खंड खिड़की के अंदर है और इसे पूरी तरह से खींचा जाना चाहिए;
2. कोड में एक ही स्थिति में एक बिट होता है, जिसका अर्थ है कि खंड खिड़की के बाहर स्थित है और खींचा नहीं जाएगा;
3. अन्य सभी मामलों में, खंड का केवल हिस्सा खिड़की में स्थित है, और इसका मतलब है कि क्लिपिंग की आवश्यकता है।

पहले दो मामलों को बिटवाइज़ लॉजिकल ऑपरेशंस का उपयोग करके आसानी से सत्यापित किया जाता है। तीसरा मामला सबसे बड़ा हित है। आइए इसे एक छोटे से ठोस उदाहरण पर विचार करें।



यदि दोनों छोर पर कोड में एक बिट होता है, तो या तो पी ₁ या पी ₂ खिड़की से बाहर अपनी सीमाओं में से एक (या इसकी निरंतरता) तक चलता है। यानी बिंदु P ₁ , R और P ₂ को इंगित करने के लिए U को इंगित करता है। नए बिंदुओं के लिए, हम फिर से चार-बिट कोड की गणना करते हैं। हमारे मामले में, खंड के छोर अभी भी खिड़की के बाहर स्थित हैं, अर्थात। हमें एक और चाल की आवश्यकता है: बिंदु R को बिंदु S पर ले जाना है, और U को बिंदु T पर ले जाना है। यह पता चला है कि कतरन प्रक्रिया संख्यात्मक है। चूंकि प्रत्येक चरण में खंड के सिरों के बीच की दूरी कम हो जाती है, हम कह सकते हैं कि एल्गोरिथ्म अभिसरण करता है। नतीजतन, एक खंड प्राप्त किया जाएगा (हमारे मामले में (एस; टी), जिसे प्रदर्शित किया जाना चाहिए)।
आइए एक और उदाहरण का उपयोग करके इस एल्गोरिथ्म के संचालन पर विचार करें।



सेगमेंट का स्थान (पी ₁ ; पी ₂ ) या तो पूर्ण दृश्यता की स्थितियों या पूर्ण अदृश्यता की शर्तों के अनुरूप नहीं है, इसलिए, इस मामले में, स्थानांतरण बिंदुओं के संचालन का भी सहारा लेते हैं।

स्थानांतरण किए जाने के बाद, खंड के सिरों के कोड दूसरी स्थिति को संतुष्ट करते हैं, अर्थात्। पूरे खंड को स्क्रीन पर प्रदर्शित नहीं किया जाएगा।

मध्यबिंदु एल्गोरिथ्म

सदरलैंड-कोहेन एल्गोरिथ्म में, खिड़की की सीमा के साथ एक लाइन खंड के चौराहे के बिंदु को खोजने से कई पुनरावृत्तियां हो सकती हैं। यदि आप बाइनरी खोज का उपयोग करके चौराहे की खोज को लागू करते हैं तो इससे बचा जा सकता है। यह विचार स्प्रेल और सदरलैंड द्वारा प्रस्तावित किया गया था। इस एल्गोरिथ्म का सॉफ्टवेयर कार्यान्वयन सदरलैंड-कोहेन एल्गोरिदम की तुलना में धीमा है, लेकिन हार्डवेयर कार्यान्वयन तेज है, क्योंकि हार्डवेयर में बुनियादी संचालन बहुत कुशलता से लागू किया जाता है।


यह विधि ऊपर वर्णित चार-बिट कोड का भी उपयोग करती है। इन कोड की मदद से, तुच्छ दृश्यता (ए) और तुच्छ अदृश्यता (बी) के मामलों का आसानी से पता लगाया जा सकता है। शेष (गैर-तुच्छ) खंडों को दो समान भागों में विभाजित किया जाता है, और दो नए प्राप्त खंडों के लिए चेक किए जाते हैं। डिवीजन और चेक तब तक किए जाएंगे जब तक खिड़की के किनारे वाले एक चौराहे का पता नहीं लग जाता है, या जब तक कोई रेखा एक बिंदु में नहीं आती है। खंड के पतन के बाद, हम इसकी दृश्यता निर्धारित करते हैं और, परिणाम के आधार पर, या तो वर्तमान में आकर्षित होते हैं या नहीं।
खंड c पर विचार करें। जाहिर है, यह खंड पूरी तरह से खिड़की के बाहर है, लेकिन इसे तुरंत अस्वीकार नहीं किया जा सकता है। यही कारण है कि हम आधा विभाजन करते हैं और खंड के कुछ हिस्सों को बाहर करते हैं। विभाजन उस समय समाप्त होता है जब खंड एक बिंदु में बदल जाता है। यह सुनिश्चित करने के बाद कि परिणामी बिंदु अदृश्य है, हम यह निष्कर्ष निकालते हैं कि पूरे खंड को खींचा नहीं जाना चाहिए।
खंड d को भी तुच्छ रूप से परिभाषित नहीं किया गया है। दो हिस्सों (बिंदु 3) में इसका विभाजन दोनों हिस्सों के लिए समान परिणाम की ओर जाता है। खंड (3; 2) को आधा बिंदु 4 से विभाजित किया गया है। सैद्धांतिक रूप से, आप पहले से ही खंड (3; 4) को आकर्षित कर सकते हैं, लेकिन यह बहुत प्रभावी नहीं है। पॉइंट 4 से सबसे दूर के दृश्यमान बिंदु के रूप में बिंदु 4 को याद रखना अधिक सही है, और खंड (4; 2) को विभाजित करना जारी रखें, जब तक कि यह खिड़की की निचली सीमा के साथ न हो जाए। परिणामी बिंदु को बिंदु 1 से सबसे दूर का दिखाई देने वाला बिंदु माना जाएगा। खंड 3; 1 को उसी तरह से संसाधित किया जाता है, और दृश्य बिंदु स्थित होता है, बिंदु 2 से सबसे दूर। फिर, इन दो बिंदुओं के बीच, ड्राइंग किया जाता है।
प्रकार के खंडों के लिए, खंड के सिरों से सबसे दूर दिखाई देने वाले बिंदुओं की दो द्विआधारी खोजों का प्रदर्शन किया जाना चाहिए। प्रकार ई के खंडों के लिए, द्विआधारी खोजों में से एक अब आवश्यक नहीं है।

किरुस-बेक एलगोरिदम

किरस-बेक एल्गोरिथ्म के काम में, अंतराल के पैरामीट्रिक प्रतिनिधित्व का उपयोग किया जाता है: P _s (t) = P ₁ + (P ₂ -P ₁ ) * t; t∈ [0; 1]। यह एल्गोरिथ्म न केवल एक आयताकार खिड़की से, बल्कि किसी भी उत्तल बहुभुज द्वारा कतरन की अनुमति देता है।
काटने वाले बहुभुज के एक अलग किनारे पर विचार करें। हम इस किनारे को सामान्य रूप से काटने वाले बहुभुज के बाहर की ओर उन्मुख करते हैं। हम यह भी मानते हैं कि कटिंग बहुभुज वामावर्त को दरकिनार करता है। फिर, यदि किनारे सदिश P _{(E (i 1 ) )} P _{E i 2 है} , तो सामान्य N _{E I} आनुपातिक होगा (y _{E i 2} -y _{E i 1} ; x _{E i 1} -x _{E i 2} )।
उस रेखा को निरूपित करें जिस पर धार L _i द्वारा निहित है। फिर क्षेत्र को सीधी रेखा से काट दिया जाता है L _i , बिंदु P से मेल खाती है जिसके लिए वैक्टर (PP _{E i} ) और N _{E i का} स्केलर उत्पाद 0 से अधिक है (P _{E i} , किनारे E _i का कोई बिंदु है)। उस रेखा के प्रतिच्छेदन का बिंदु जिस पर खंड कट-ऑफ लाइन L _{i के साथ} स्थित है, समीकरण से पाया जाता है ((P _s (t) -P _{E i} , N _{E i} = 0. इस समीकरण को हल करते हुए, हम t पाते हैं।
वर्णित एल्गोरिथ्म के लिए, यह भी महत्वपूर्ण है कि किस दिशा में (खिड़की के अंदर या बाहर) पी ₁ से पी ₂ से एक खंड के साथ आगे बढ़ने पर बिंदु गुजरता है। यह संकेत द्वारा निर्धारित किया जाता है ((पी ₂ पी ₁ ), एन _{ई i} । हम इस तरह के चौराहे बिंदुओं को निरूपित करेंगे:



निर्देशांक के बाद सभी संभावित चौराहों के लिए लाइनों की गणना की गई है L _{i के साथ} , किसी को संभावित आवक से अधिकतम समन्वय चुनना चाहिए और संभावित आउटगोइंग से न्यूनतम होना चाहिए (t _VxMax ; t _OutMin )। यदि वह रेखा जिस पर खंड P ₁ P ₂ स्थित है, कट-ऑफ बहुभुज को काटता है, तो _{B BMMax} <t _OutMin । इस स्थिति में, यदि चौराहा [t ₁ , t ₂ ] = [t _InxMax , t _OutMin ] 1 [0,1] गैर- _{रिक्त} है, तो P _s (t ₁ ) P _s (t ₂ ) वांछित कट-ऑफ सेगमेंट होगा, अन्यथा इस मामले में, यह खंड पूरी तरह से कट-ऑफ क्षेत्र के बाहर है।

कतरन विषय, निश्चित रूप से, इन एल्गोरिदम पर समाप्त नहीं होता है। एक अलग मुद्दा बहुभुज कतरन एल्गोरिदम है। यदि विषय हब्रोसैक्विटी के लिए दिलचस्प होगा, तो मैं निश्चित रूप से इस विषय को प्रकट करूंगा।