इस आलेख में स्टीरियो विजन में प्रयुक्त गणितीय उपकरण के बारे में बुनियादी जानकारी है। यह लिखने के बारे में विचार तब आया जब मैंने स्टीरियो विज़न विधियों के साथ काम करना शुरू किया, विशेष रूप से, ओपनसीवी में लागू एल्गोरिदम का उपयोग करते हुए। ये एल्गोरिदम अक्सर विभिन्न अवधारणाओं को संदर्भित करते हैं, जैसे कि "मौलिक मैट्रिक्स", "एपीपोलर ज्यामिति", "ट्राइंगुलेशन"। कंप्यूटर दृष्टि पर बहुत अच्छी किताबें हैं, जो वर्णन करती हैं, जिसमें स्टीरियो दृष्टि और सभी आवश्यक अवधारणाएं शामिल हैं, लेकिन वे अक्सर एक शुरुआत के लिए बहुत अधिक जानकारी रखते हैं। यहाँ, संक्षिप्त रूप में, स्टीरियो विज़न कैसे काम करता है और इसके साथ जुड़ी बुनियादी आवश्यक अवधारणाओं के बारे में बुनियादी जानकारी:

• अनुमानित ज्यामिति और वर्दी निर्देशांक
• कैमरा मॉडल
• एपिपोलर ज्यामिति (एपिपोरल जियोमेटी), मौलिक और आवश्यक मैट्रिक्स (फंडामेंटल मैट्रिक्स, आवश्यक मैट्रिक्स)
• अंकों के एक स्टीरियो जोड़ी की त्रिकोणासन
• गहराई का नक्शा, असमानता का नक्शा और इसकी गणना के पीछे का विचार

इस लेख की लगभग सभी सामग्री हार्टले, आरआई और ज़िसरमैन, ए। की पुस्तक "मल्टीपल व्यू ज्योमेट्री इन कंप्यूटर विज़न" पर आधारित है, और एक गहन मानचित्र बनाने वाले खंड का वर्णन ग्रेग ब्रैडस्की, एड्रियन केहलर द्वारा लर्निंग ओपनसीवी की सामग्री के आधार पर किया गया है ।

लेख की सामग्री को समझने के लिए, विश्लेषणात्मक ज्यामिति और रैखिक बीजगणित का एक सामान्य विचार होना पर्याप्त है: यह जानने के लिए कि मैट्रिक्स, वेक्टर, स्केलर और वेक्टर उत्पाद क्या हैं।

1 प्रक्षेप्य ज्यामिति और सजातीय निर्देशांक

स्टैक्टिव विज़न ज्यामिति में प्रोजेक्टिव ज्योमेट्री एक महत्वपूर्ण भूमिका निभाती है । प्रायोगिक ज्यामिति के कई दृष्टिकोण हैं: ज्यामितीय (यूक्लिडियन ज्यामिति, स्वयंसिद्ध और ज्यामितीय वस्तुओं की अवधारणा को पेश करने के लिए और एक प्रक्षेप्य स्थान के सभी गुणों को प्राप्त करने के लिए), विश्लेषणात्मक (निर्देशांक में सब कुछ पर विचार करने के लिए, यूक्लिडियन ज्यामिति के लिए एक विश्लेषणात्मक दृष्टिकोण के रूप में)।

आगे की चर्चा के लिए, हमें मुख्य रूप से प्रोजेक्टिव ज्यामिति के लिए विश्लेषणात्मक दृष्टिकोण की समझ की आवश्यकता होगी, और यह वह है जो नीचे प्रस्तुत किया गया है।

प्रक्षेप्य तल के बिंदु। द्वि-आयामी प्रक्षेप्य स्थान पर विचार करें (जिसे एक प्रक्षेपवक्र विमान भी कहा जाता है)। जबकि एक नियमित यूक्लिडियन विमान पर, बिंदुओं को निर्देशांक ( x , y ) ^T की एक जोड़ी द्वारा वर्णित किया जाता है, एक प्रक्षेप्य तल पर, बिंदुओं को तीन-घटक वेक्टर ( x , y , w ) ^T द्वारा वर्णित किया जाता है ^। इसके अलावा, किसी भी नॉनजेरो संख्या a के लिए , वैक्टर ( x , y , w ) ^T और ( ax , ay , aw ) ^T एक ही बिंदु के अनुरूप हैं। और शून्य वेक्टर (0,0,0) ^टी किसी भी बिंदु के अनुरूप नहीं है और इसे विचार से बाहर कर दिया जाता है। समतल बिंदुओं के इस तरह के विवरण को सजातीय निर्देशांक कहा जाता है।

प्रक्षेप्य तल के बिंदुओं को साधारण यूक्लिडियन विमान के बिंदुओं के साथ जोड़ा जा सकता है। समन्वय वेक्टर ( x , y , w ) ^{T के} लिए w we 0 के लिए, हम यूक्लिडियन विमान के बिंदु को निर्देशांक ( x / w , y / w ) ^{T से जोड़ते हैं।} यदि w = 0, अर्थात निर्देशांक वेक्टर का रूप ( x , y , 0 ^T ) है, तो हम कहते हैं कि यह बिंदु अनंत पर है। इस प्रकार, अनुमानित विमान को अनंत काल के बिंदुओं द्वारा पूरक एक यूक्लिडियन विमान माना जा सकता है।

आप सजातीय निर्देशांक ( x , y , w ) ^T से सामान्य यूक्लिडियन निर्देशांक से अंतिम घटक द्वारा समन्वयित वेक्टर को विभाजित कर सकते हैं और फिर इसे ( x , y , w ) ^T → ( x / w , y / w ) ^{T से हटा सकते हैं।} और यूक्लिडियन निर्देशांक ( x , y ) ^{T से} हम एक के साथ समन्वय वेक्टर के पूरक द्वारा सजातीय पर जा सकते हैं: ( x , y ) ^T → ( x , y , 1) ^T

प्रक्षेप्य तल पर रेखाएँ। प्रक्षेपक तल पर किसी भी रेखा का वर्णन तीन घटक वेक्टर l = ( a , b , c ) ^T द्वारा एक बिंदु की तरह किया जाता है ^। फिर से, रेखा का वर्णन करने वाला वेक्टर एक गैर-अक्षीय कारक तक निर्धारित होता है। इस स्थिति में, रेखा के समीकरण का रूप होगा: l ^T x = 0।

मामले में जब एक ² + बी ² case 0, हमारे पास सामान्य सीधी रेखा कुल्हाड़ी का एक एनालॉग + बाइ + सी = 0. होता है और वेक्टर (0,0, w ) अनंत पर पड़ी एक सीधी रेखा से मेल खाती है।

त्रि-आयामी प्रक्षेप्य स्थान। प्रक्षेप्य समतल के अनुरूप, त्रि-आयामी प्रक्षेप्य स्थान के बिंदु समरूप निर्देशांक ( x , y , z , w ) ^T के चार घटक सदिश द्वारा निर्धारित किए जाते हैं ^। फिर से, किसी भी नॉनजेरो संख्या a के लिए , समन्वित वैक्टर ( x , y , z , w ) ^T और ( ax , ay , az , aw ) ^T एक ही बिंदु के अनुरूप होते हैं।

जैसा कि प्रक्षेपी विमान के मामले में, तीन आयामी यूक्लिडियन अंतरिक्ष और तीन आयामी प्रक्षेप्य स्थान के बिंदुओं के बीच एक पत्राचार स्थापित किया जा सकता है। सजातीय निर्देशांक का सदिश ( x , y , z , w ) ^{T के} लिए w inates 0 निर्देशांक के साथ यूक्लिडियन स्थान में एक बिंदु से मेल खाती है ( x / w , y / w , z / w ) ^T। और फॉर्म ( x , y , z , 0) ^T के सजातीय निर्देशांक के वेक्टर के साथ एक बिंदु के बारे में वे कहते हैं कि यह अनंत पर स्थित है।

प्रक्षेप्य परिवर्तन। एक और चीज जो आगे की प्रस्तुति के लिए आवश्यक होगी वह है प्रोजैक्टिव ट्रांसफॉर्मेशन (होमोग्राफी, प्रोजक्टिव ट्रांसफॉर्मेशन - अंग्रेजी साहित्य में)। एक ज्यामितीय दृष्टिकोण से, एक प्रक्षेपी परिवर्तन एक प्रक्षेपी विमान (या स्थान) का एक प्रतिवर्ती रूपांतरण है जो सीधी रेखाओं को सीधी रेखाओं में परिवर्तित करता है। निर्देशांक में, प्रक्षेपी परिवर्तन को गैर-अध: पतन वर्ग मैट्रिक्स H के रूप में व्यक्त किया जाता है, जबकि निर्देशांक सदिश x निम्नलिखित सूत्र के अनुसार समन्वय सदिश x 'में जाता है: x ' = H x ।

2 प्रोजेक्टिव कैमरा मॉडल

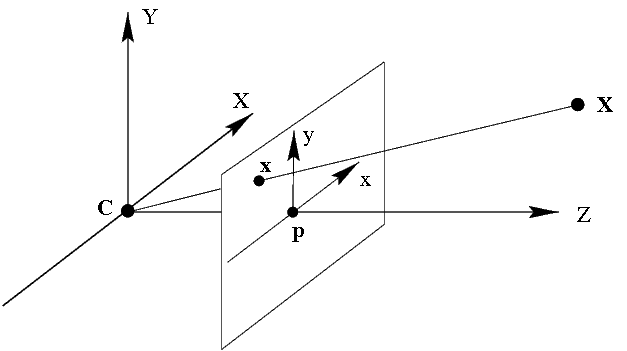
चित्र 1: कैमरा मॉडल। C कैमरे का केंद्र है, Cp कैमरे का मुख्य अक्ष है। तीन आयामी अंतरिक्ष के बिंदु X को बिंदु x - छवि तल पर प्रक्षेपित किया जाता है।

आधुनिक सीसीडी कैमरों को निम्नलिखित मॉडल का उपयोग करके अच्छी तरह से वर्णित किया जाता है, जिसे एक प्रोजेक्टिव कैमरा, पिनहोल कैमरा कहा जाता है। प्रोजेक्टिव कैमरा को कैमरे के केंद्र , मुख्य अक्ष - कैमरे के केंद्र में शुरू होने वाले बीम और जहां कैमरा देख रहा है, वहां से निर्देशित किया जाता है, छवि विमान - जिस विमान पर अंक लगाए जाते हैं, और इस विमान पर समन्वय प्रणाली। इस तरह के एक मॉडल में, अंतरिक्ष एक्स में एक मनमाना बिंदु छवि विमान पर खंड सीएक्स पर झूठ बोलने वाले बिंदु पर अनुमानित होता है, जो शुरुआती बिंदु एक्स (छवि 1 देखें) के साथ कैमरा सी के केंद्र को जोड़ता है।

प्रक्षेपण सूत्र में समरूप निर्देशांक में एक सरल गणितीय संकेतन है:

एक्स = पी एक्स

जहाँ X अंतरिक्ष में एक बिंदु के सजातीय निर्देशांक हैं, x विमान में एक बिंदु के सजातीय निर्देशांक हैं, P 3 × 4 कैमरा मैट्रिक्स है।

मैट्रिक्स P को P = KR [ I | - c ] = के [ R | t ], जहां K एक 3 × 3 कैमरा के आंतरिक मापदंडों का ऊपरी त्रिकोणीय मैट्रिक्स है (एक विशिष्ट दृश्य नीचे दिया गया है), R एक 3 × 3 ऑर्थोगोनल मैट्रिक्स है जो वैश्विक समन्वय प्रणाली के सापेक्ष कैमरे के रोटेशन को निर्धारित करता है, मैं एक 3 × 3 पहचान मैट्रिक्स, वेक्टर हूं सी - कैमरे के केंद्र के निर्देशांक, और टी = - आर सी ।

यह ध्यान दिया जाना चाहिए कि कैमरा मैट्रिक्स एक निरंतर नॉनज़रो फैक्टर तक निर्धारित होता है, जो सूत्र x = P X का उपयोग करके प्रोजेक्टिंग पॉइंट के परिणामों को नहीं बदलेगा। हालांकि, यह स्थिर कारक आमतौर पर चुना जाता है ताकि कैमरा मैट्रिक्स में ऊपर वर्णित रूप हो।

सरलतम स्थिति में, जब कैमरा का केंद्र मूल में होता है, तो कैमरे का मुख्य अक्ष Cz अक्ष के साथ संरेखित होता है, कैमरा प्लेन पर समन्वित अक्षों का स्केल (जो वर्ग पिक्सेल के बराबर होता है) होता है, और छवि के केंद्र में शून्य निर्देशांक होते हैं, कैमरा मैट्रिक्स P = K होगा [ मैं | ० ], कहाँ

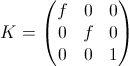
वास्तविक सीसीडी कैमरों में, पिक्सेल आमतौर पर वर्ग वाले से थोड़ा अलग होते हैं, और छवि के केंद्र में गैर-शून्य निर्देशांक होते हैं। इस स्थिति में, आंतरिक मापदंडों का मैट्रिक्स रूप लेगा:

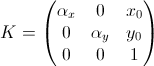
गुणांक f , α _x , α _y - को कैमरे की फोकल लंबाई (क्रमशः, सामान्य और x और y कुल्हाड़ियों के साथ) कहा जाता है।

इसके अलावा, प्रकाशिकी की अपूर्ण प्रकृति के कारण, कैमरों से प्राप्त छवियों में विकृति विकृतियां होती हैं। इन विकृतियों का एक ग़ैर-गणितीय रिकॉर्ड है:

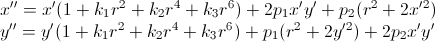
जहां k ₁ , k ₂ , p ₁ , p ₂ , k ₃ विकृति गुणांक हैं, जो ऑप्टिकल सिस्टम के पैरामीटर हैं; r ² = x ' ² + y ' ² ; ( x ', y ') - वर्ग पिक्सेल के साथ छवि के केंद्र और विरूपण की अनुपस्थिति के सापेक्ष एक बिंदु के प्रक्षेपण के निर्देशांक; ( x coord , y y ) - वर्ग पिक्सेल में छवि के केंद्र के सापेक्ष बिंदु के विकृत निर्देशांक।

विकृतियां ऑब्जेक्ट की दूरी पर निर्भर नहीं करती हैं, बल्कि केवल उन बिंदुओं के निर्देशांक पर निर्भर करती हैं, जिस पर ऑब्जेक्ट के पिक्सल का अनुमान लगाया जाता है। तदनुसार, विकृतियों की भरपाई के लिए, आमतौर पर कैमरे से प्राप्त मूल छवि को परिवर्तित किया जाता है। यह परिवर्तन कैमरे से प्राप्त सभी छवियों के लिए समान होगा, बशर्ते कि फोकल लंबाई स्थिर (गणितीय रूप से, आंतरिक मापदंडों के समान मैट्रिक्स) हो।

ऐसी स्थिति में जहां कैमरे के आंतरिक मापदंडों को जाना जाता है और विरूपण गुणांक कहते हैं कि कैमरा कैलिब्रेटेड है।

3 जोड़ी कैमरे

कम से कम दो कैमरे होने पर, प्रेक्षित बिंदुओं के त्रि-आयामी निर्देशांक निर्धारित करने के बारे में बात कर सकते हैं।

कैमरों की एक जोड़ी के अंश, अंशांकन। आज्ञा देना दो कैमरों को उनके मैट्रिक्स P और P द्वारा परिभाषित किया गया है कुछ समन्वय प्रणाली में। इस मामले में, वे कहते हैं कि कैलिब्रेटेड कैमरों की एक जोड़ी है। यदि कैमरों के केंद्र संयोग नहीं करते हैं, तो कैमरों की इस जोड़ी का उपयोग प्रेक्षित बिंदुओं के त्रि-आयामी निर्देशांक को निर्धारित करने के लिए किया जा सकता है।

अक्सर, समन्वय प्रणाली को चुना जाता है ताकि कैमरा मैट पी = के [ I | 0] के रूप में हो, P '= K ' [ R '| टी ']। यह हमेशा किया जा सकता है यदि आप उस मूल का चयन करते हैं जो पहले कैमरे के केंद्र के साथ मेल खाता है और इसके ऑप्टिकल अक्ष के साथ जेड अक्ष को निर्देशित करता है।

कैमरों का कैलिब्रेशन आमतौर पर किया जाता है, एक अंशांकन टेम्पलेट की कई शूटिंग के कारण, मुख्य बिंदुओं को आसानी से उस छवि में पहचाना जा सकता है जिसके लिए अंतरिक्ष में उनके सापेक्ष स्थान ज्ञात हैं। अगला, समीकरणों के सिस्टम संकलित और हल किए गए हैं (लगभग), अनुमानों के निर्देशांक, कैमरा मैट्रिक्स और अंतरिक्ष में टेम्पलेट के बिंदुओं की स्थिति को जोड़ते हैं।

आमतौर पर अंशांकन एल्गोरिदम के उपलब्ध कार्यान्वयन होते हैं, जैसे कि मैटलैब कैलिब्रेशन टूलबॉक्स । OpenCV लाइब्रेरी में कैमरों को कैलिब्रेट करने और छवि में अंशांकन टेम्पलेट की खोज के लिए एल्गोरिदम भी शामिल हैं।

एपीपोलर ज्यामिति। अंकों के त्रि-आयामी निर्देशांक की गणना करने की वास्तविक विधि के वर्णन के लिए आगे बढ़ने से पहले, मैं कुछ महत्वपूर्ण ज्यामितीय गुणों का वर्णन करूंगा जो दोनों कैमरों से छवियों पर तीन-आयामी अंतरिक्ष के एक बिंदु के अनुमानों से संबंधित हैं।

चित्रा 2: एपिपोलर ज्यामिति

बता दें कि दो कैमरे हैं, जैसा कि चित्र 2 में दिखाया गया है। सी पहले कैमरे का केंद्र है, सी 'दूसरे कैमरे का केंद्र है। स्पेस X के बिंदु को बाएं कैमरे के इमेज प्लेन पर x और 'सही कैमरे के इमेज प्लेन पर' x पर प्रोजेक्ट किया जाता है। बाएँ कैमरे की छवि में बिंदु x का प्रोटोटाइप किरण xX है । इस बीम को एक सीधी रेखा l 'में दूसरे कक्ष के तल पर प्रक्षेपित किया जाता है, जिसे एपीपोलर रेखा कहा जाता है। दूसरे कैमरे के इमेज प्लेन पर बिंदु X की छवि अनिवार्य रूप से एपिपोलर लाइन l 'पर स्थित है।

इस प्रकार, बाएं कैमरे की छवि में प्रत्येक बिंदु x सही कैमरा की छवि में एक एपिपोलर लाइन l से मेल खाता है। इस मामले में, सही कैमरे की छवि में x के लिए जोड़ी केवल संबंधित एपिपोलर लाइन पर झूठ हो सकती है। इसी प्रकार, दाईं ओर की छवि में प्रत्येक बिंदु x 'बाईं ओर एक एपिपोलर लाइन l से मेल खाता है।

एपीपोलर ज्योमेट्री का उपयोग स्टीरोपॉपर्स की खोज के लिए किया जाता है, और यह सत्यापित करने के लिए कि अंकों की एक जोड़ी एक स्टीरियोपेयर (यानी, अंतरिक्ष में कुछ बिंदु का एक प्रक्षेपण) हो सकती है।

निर्देशांक में एपिपोलर ज्यामिति की एक बहुत ही सरल संकेतन है। आज्ञा देना एक जोड़ी कैमरों की हो, और x एक कैमरे की छवि में बिंदु के समान निर्देशांक हो, और x 'दूसरे की छवि में हो। एक 3 × 3 मैट्रिक्स F मौजूद है, जैसे कि x , x 'की एक जोड़ी एक स्टीरियो जोड़ी है यदि और केवल यदि:

x ' T F x = 0

मैट्रिक्स F को मूलभूत मैट्रिक्स कहा जाता है। इसकी रैंक 2 है, यह एक नॉनजेरो फैक्टर तक निर्धारित है और केवल स्रोत कैमरों पी और पी 'के मेट्रिसेस पर निर्भर करता है।

मामले में जब कैमरे के सरणियों में फॉर्म P = K [ I | 0], P '= K ' [ R होता है t ] मूलभूत मैट्रिक्स की गणना सूत्र द्वारा की जा सकती है:

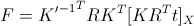
जहाँ वेक्टर के लिए संकेतन [ e ] _{X की} गणना की जाती है

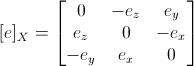
मौलिक मैट्रिक्स का उपयोग करते हुए, एपिपोलर लाइनों के समीकरणों की गणना की जाती है। बिंदु x के लिए , एपिपोलर लाइन को परिभाषित करने वाले वेक्टर में फॉर्म l '= F x होगा , और एपिपोलर लाइन के समीकरण में l ' ^T x '= 0 होगा। इसी प्रकार पॉइंट x के लिए, एपिलेटर लाइन को परिभाषित करने वाले वेक्टर का फॉर्म l = होगा। एफ ^टी एक्स ’।

मौलिक मैट्रिक्स के अलावा, एक आवश्यक मैट्रिक्स के रूप में ऐसी चीज है: ई = के ' ^टी एफ के । मामले में जब आंतरिक मापदंडों के मैट्रिक्स एकता होते हैं, तो आवश्यक मैट्रिक्स मौलिक के साथ मेल खाएगा। आवश्यक मैट्रिक्स का उपयोग करके, आप पहले के सापेक्ष दूसरे कैमरे की स्थिति और रोटेशन को पुनर्स्थापित कर सकते हैं, इसलिए इसका उपयोग उन कार्यों में किया जाता है जिसमें आपको कैमरे की गति निर्धारित करने की आवश्यकता होती है।

अंकों का त्रिकोणासन (त्रिकोणासन)। अब आइए इसके बिंदुओं के निर्देशांक से एक बिंदु के तीन आयामी निर्देशांक को कैसे निर्धारित किया जाए। इस प्रक्रिया को साहित्य में त्रिकोणासन कहा जाता है।

बता दें कि मैट्रिसेस पी ₁ और पी _{2 के} साथ दो कैलिब्रेटेड कैमरे हैं। x ₁ और x ₂ , अंतरिक्ष X के एक बिंदु के सजातीय प्रक्षेपण निर्देशांक हैं। तब आप समीकरणों की निम्न प्रणाली बना सकते हैं:

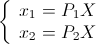
व्यवहार में, इस प्रणाली को हल करने के लिए निम्नलिखित दृष्टिकोण लागू किया जाता है। सदिश रूप से पहले समीकरण को x _{1 से} गुणा करें, दूसरे को x _{2 से} , रैखिक रूप से निर्भर समीकरणों से छुटकारा पाएं और सिस्टम को A X = 0 के रूप में लाएं, जहां A का आकार 4 × 4 है। फिर हम या तो उससे आगे बढ़ सकते हैं कि वेक्टर X बिंदु के समरूप निर्देशांक है, इसका अंतिम घटक 1 के बराबर है और तीन अज्ञात के साथ 3 समीकरणों के परिणामस्वरूप प्रणाली को हल करता है। एक वैकल्पिक तरीका यह है कि सिस्टम ए एक्स = 0 का कोई भी नॉनजेरो सॉल्यूशन लिया जाए, उदाहरण के लिए, मैट्रिक्स ए की सबसे छोटी एकवचन संख्या के अनुरूप एक विलक्षण वेक्टर के रूप में गणना की जाती है ।

4 गहराई का नक्शा बनाना

एक गहराई का नक्शा एक छवि है, जिस पर प्रत्येक पिक्सेल के लिए, रंग के बजाय, कैमरे के लिए इसकी दूरी संग्रहीत होती है। गहराई का नक्शा एक विशेष गहराई वाले कैमरे का उपयोग करके प्राप्त किया जा सकता है (उदाहरण के लिए, किनेक्ट सेंसर इस तरह का एक कैमरा है), और इसका निर्माण छवियों के एक स्टीरियो जोड़े का उपयोग करके भी किया जा सकता है।

एक स्टीरियो जोड़ी का उपयोग करके एक गहन मानचित्र बनाने के पीछे का विचार बहुत सरल है। एक छवि में प्रत्येक बिंदु के लिए, यह दूसरी छवि में बिंदुओं की एक जोड़ी की खोज करता है। और इसी बिंदुओं की एक जोड़ी से, आप त्रिभुज प्रदर्शन कर सकते हैं और तीन आयामी अंतरिक्ष में उनकी उलटा छवि के निर्देशांक निर्धारित कर सकते हैं। प्रोटोटाइप के तीन आयामी निर्देशांक को जानने के बाद, गहराई को कैमरे के विमान की दूरी के रूप में गणना की जाती है।

युग्मित बिंदु को एपिपोलर लाइन पर मांगना चाहिए। तदनुसार, खोज को सरल बनाने के लिए, छवियों को गठबंधन किया जाता है ताकि सभी एपिपोलर लाइनें छवि के किनारों (आमतौर पर क्षैतिज) के समानांतर हों। इसके अलावा, छवियों को संरेखित किया जाता है ताकि निर्देशांक ( x ₀ , y ₀ ) के साथ एक बिंदु के लिए इसी एपिपोलर लाइन को समीकरण x = x ₀ द्वारा दिया जाता है, फिर प्रत्येक बिंदु के लिए इसी जोड़ी को दूसरे के साथ छवि में एक ही पंक्ति में खोजा जाना चाहिए कैमरा। छवि संरेखण की इस प्रक्रिया को सुधार कहा जाता है। आमतौर पर, सुधार को फिर से इमेजेटिंग द्वारा किया जाता है और विरूपण से छुटकारा मिलता है। आयतित चित्रों का एक उदाहरण चित्र 3 में दिखाया गया है, चित्रों को चित्रों के एक डेटाबेस से लिया गया है जो गहराई के नक्शे http://vision.middlebury.edu/stereo के निर्माण के लिए विभिन्न तरीकों की तुलना करता है।

चित्र 3: सुधारा गया चित्रों का एक उदाहरण है, और उनके संबंधित विषमता का नक्शा।

छवियों को सुधारने के बाद, बिंदुओं के संबंधित जोड़े की खोज करें। सबसे सरल विधि चित्र 4 में दी गई है और इसमें निम्नलिखित शामिल हैं। निर्देशांक ( x ₀ , y ₀ ) के साथ बाईं छवि के प्रत्येक पिक्सेल के लिए, एक पिक्सेल खोज सही छवि पर की जाती है। यह माना जाता है कि सही तस्वीर में पिक्सेल में निर्देशांक ( x ₀ - d , y ₀ ) होना चाहिए, जहां d को असमानता कहा जाता है। संबंधित पिक्सेल की खोज प्रतिक्रिया फ़ंक्शन की अधिकतम गणना करके की जाती है, जो उदाहरण के लिए, पिक्सेल पिक्सेल का सहसंबंध हो सकता है। परिणाम एक असमानता मानचित्र है, जिसका एक उदाहरण अंजीर में दिखाया गया है। 3।

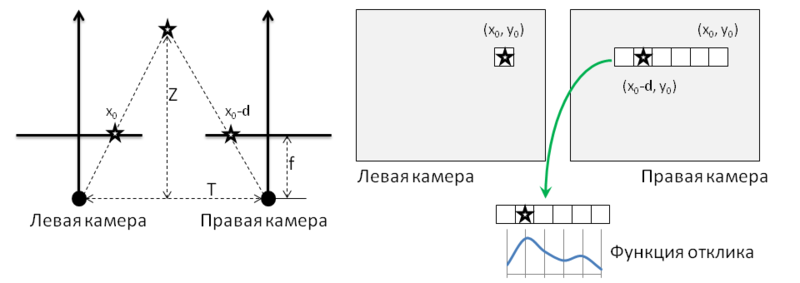
चित्र 4: गहराई के नक्शे की गणना।

वास्तविक गहराई मूल्य पिक्सेल विस्थापन के परिमाण के विपरीत आनुपातिक हैं। यदि हम चित्र 4 के बाएं आधे भाग पर अंकन का उपयोग करते हैं, तो असमानता और गहराई के बीच संबंध निम्नलिखित तरीके से व्यक्त किए जा सकते हैं:

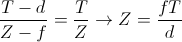
गहराई और विस्थापन के बीच व्युत्क्रम संबंध के कारण, इस विधि के आधार पर काम करने वाले स्टीरियो विज़न सिस्टम का रिज़ॉल्यूशन कम दूरी पर बेहतर होता है और दूर की दूरी पर बदतर होता है।