👐🏾 👨🏿‍🤝‍👨🏻 🔡 गेम डेवलपर्स के लिए रैखिक बीजगणित 🎱 👩🏽‍⚕️ 💾

यह लेख एक चार-लेख श्रृंखला का अनुवाद है, गेम डेवलपर्स के लिए रेखीय बीजगणित, रैखिक बीजगणित पर डेविड रोसेन द्वारा लिखित और खेल के विकास में इसका अनुप्रयोग। मूल लेख यहां देखे जा सकते हैं: भाग 1 , भाग 2 , भाग 3 और भाग 4 मैंने अलग-अलग विषयों में अनुवाद प्रकाशित नहीं किए, लेकिन सभी लेखों को एक में जोड़ दिया। मुझे लगता है कि सामग्री को समझना और उसके साथ काम करना अधिक सुविधाजनक होगा। तो चलिए शुरू करते हैं।

हमें रैखिक बीजगणित की आवश्यकता क्यों है?

रैखिक बीजगणित में दिशाओं में से एक वैक्टर का अध्ययन है। यदि आपका गेम ऑन-स्क्रीन बटन की स्थिति, कैमरा और इसकी दिशा, ऑब्जेक्ट की गति के साथ काम करता है, तो आपको वैक्टर से निपटना होगा। जितना बेहतर आप रैखिक बीजगणित को समझते हैं, उतना अधिक नियंत्रण आपको वैक्टर के व्यवहार पर मिलता है और इसलिए, आपके खेल पर।

वेक्टर क्या है?

खेलों में, स्थानों, दिशाओं और गति को संग्रहीत करने के लिए वैक्टर का उपयोग किया जाता है। निम्नलिखित एक दो आयामी वेक्टर का एक उदाहरण है:

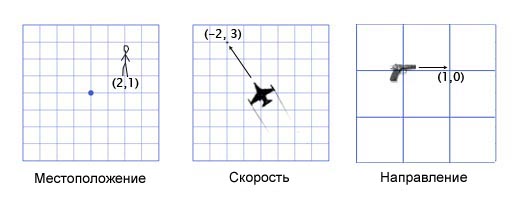
स्थान वेक्टर (जिसे "त्रिज्या वेक्टर" भी कहा जाता है) इंगित करता है कि एक व्यक्ति प्रारंभिक बिंदु से दो मीटर पूर्व और एक मीटर उत्तर में है। वेग वेक्टर से पता चलता है कि समय की एक इकाई के लिए विमान तीन किलोमीटर ऊपर और दो किलोमीटर बाईं ओर चलता है। दिशा वेक्टर हमें बताता है कि बंदूक सही ओर इशारा कर रही है।

जैसा कि आप देख सकते हैं, वेक्टर केवल संख्याओं का एक सेट है जो संदर्भ के आधार पर एक या किसी अन्य अर्थ पर ले जाता है। उदाहरण के लिए, वेक्टर (1, 0) दोनों हथियार के लिए दिशा हो सकता है, जैसा कि चित्र में दिखाया गया है, और संरचना का निर्देशांक आपकी वर्तमान स्थिति से एक मील पूर्व में है। या एक घोंघा की गति जो 1 मील प्रति घंटे की गति से सही चलती है ( अनुवादक का ध्यान दें: घोंघे के लिए बहुत तेज़, प्रति सेकंड 44 सेंटीमीटर )।

इकाइयों पर नज़र रखना महत्वपूर्ण है। मान लीजिए कि हमारे पास एक वेक्टर V (3,5,2) है। यह हमें कम बताता है। तीन क्यों, पाँच क्यों? हमारे अतिवृद्धि खेल में, मीटर में दूरी और प्रति सेकंड मीटर में गति का संकेत दिया जाता है। इस सदिश में पहली संख्या पूर्व दिशा है, दूसरी ऊपर की दिशा है, तीसरी उत्तर दिशा है। नकारात्मक संख्याएं विपरीत दिशाओं, पश्चिम, नीचे और दक्षिण को दर्शाती हैं। वेक्टर V (3,5,2) द्वारा परिभाषित स्थान पूर्व में तीन मीटर, शीर्ष पर पांच मीटर और उत्तर में दो मीटर की दूरी पर स्थित है, जैसा कि नीचे दी गई तस्वीर में दिखाया गया है।

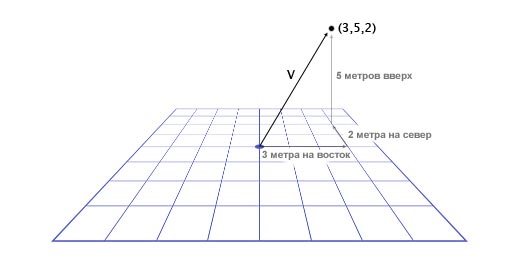
इसलिए, हमने वैक्टर के साथ काम करने की मूल बातें सीख ली हैं। अब हम सीखते हैं कि वैक्टर का उपयोग कैसे करें।

वेक्टर जोड़

वैक्टर जोड़ने के लिए, हमें बस उनके प्रत्येक घटक को एक दूसरे से जोड़ना होगा। उदाहरण के लिए:

(0, 1, 4) + (3, -2, 5) = (0 + 3, 1-2, 4 + 5) = (3, -1, 9)

हमें वैक्टर जोड़ने की आवश्यकता क्यों है? अधिकांश समय, खेलों में वेक्टर जोड़ का उपयोग शारीरिक एकीकरण के लिए किया जाता है। किसी भी भौतिक वस्तु में स्थान, गति और त्वरण के लिए वैक्टर होंगे। प्रत्येक फ्रेम के लिए (आमतौर पर एक सेकंड का एक छठा), हमें दो वैक्टर को एकीकृत करना चाहिए: गति में गति और गति में गति को जोड़ना।

आइए मारियो जंपिंग उदाहरण देखें। यह स्थिति (0, 0) से शुरू होता है। फिलहाल कूद शुरू होता है, इसकी गति (1, 3), यह जल्दी से ऊपर और दाईं ओर बढ़ता है। इसका त्वरण (0, -1) है, क्योंकि गुरुत्वाकर्षण इसे नीचे खींचता है। चित्र में दिखाया गया है कि उसका कूदना कैसा दिखता है, सात फ्रेम में टूट गया। ब्लैक टेक्स्ट प्रत्येक फ्रेम में अपनी गति दिखाता है।

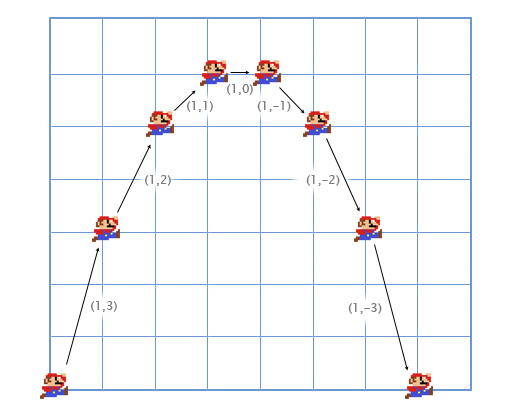
आइए यह समझने के लिए कि कैसे सब कुछ होता है, पहले फ्रेम को और अधिक विस्तार से देखें।

पहले फ्रेम के लिए, हम मारियो (1, 3) की गति को इसके स्थान (0, 0) में जोड़ते हैं और इसके नए निर्देशांक (1, 3) प्राप्त करते हैं। फिर हम इसकी गति (1, 3) के साथ त्वरण (0, -1) जोड़ते हैं और मारियो की गति (1, 2) के लिए एक नया मूल्य प्राप्त करते हैं।

दूसरे फ्रेम के लिए भी ऐसा ही करें। गति (1, 2) को स्थान (1, 3) में जोड़ें और निर्देशांक (2, 5) प्राप्त करें। फिर हम त्वरण (0, -1) को इसकी गति (1, 2) में जोड़ते हैं और एक नई गति (1, 1) प्राप्त करते हैं।

आमतौर पर, खिलाड़ी कीबोर्ड या गेमपैड का उपयोग करके खेल चरित्र के त्वरण को नियंत्रित करता है, और खेल बदले में, भौतिक जोड़ (वैक्टर के अलावा) के माध्यम से गति और स्थान के लिए नए मूल्यों की गणना करता है। यह वही समस्या है जो अभिन्न कलन में हल होती है , हम इसे अपने खेल के लिए बहुत सरल करते हैं। मैंने ध्यान दिया कि अभिन्न कलन पर व्याख्यान को ध्यान से सुनना मेरे लिए बहुत आसान है, इसके व्यावहारिक अनुप्रयोग के बारे में सोचना, जिसे हमने अभी वर्णित किया है।

वैक्टर का घटाव

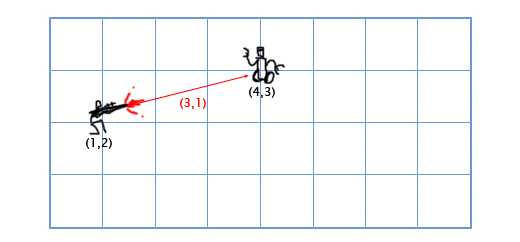
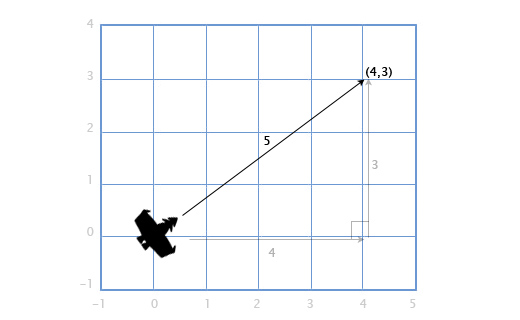
घटाव की गणना उसी सिद्धांत के अनुसार की जाती है - हम वैक्टर के संगत घटकों को घटाते हैं। वेक्टर को घटाना एक वेक्टर प्राप्त करने के लिए सुविधाजनक है जो एक स्थान से दूसरे स्थान पर दिखाता है। उदाहरण के लिए, मान लीजिए कि एक खिलाड़ी एक लेजर गन के साथ निर्देशांक (1, 2) पर स्थित है, और एक शत्रु रोबोट निर्देशांक (4, 3) पर स्थित है। रोबोट को हिट करने वाले लेजर बीम के मोशन वेक्टर को निर्धारित करने के लिए, हमें खिलाड़ी के स्थान को रोबोट के स्थान से घटाना होगा। हमें मिलता है:

(४, ३) - (१, २) = (४-१, ३-२) = (३, १)।

एक वेक्टर को स्केलर द्वारा गुणा करना

जब हम वैक्टर के बारे में बात करते हैं, तो हम व्यक्तिगत संख्या को स्केलर कहते हैं। उदाहरण के लिए (3, 4) एक सदिश राशि है, और 5 एक अदिश राशि है। खेलों में, अक्सर एक वेक्टर को एक संख्या (स्केलर) से गुणा करना आवश्यक होता है। उदाहरण के लिए, प्रत्येक फ्रेम में खिलाड़ी की गति को 0.9 से गुणा करके सरल वायु प्रतिरोध का अनुकरण करना। ऐसा करने के लिए, हमें वेक्टर के प्रत्येक घटक को एक स्केलर द्वारा गुणा करना होगा। यदि खिलाड़ी की गति (10, 20) है, तो नई गति होगी:

0.9 * (10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18)।

वेक्टर लंबाई

यदि हमारे पास एक वेग वेक्टर वी (4, 3) के साथ एक जहाज है, तो हमें यह भी पता लगाना होगा कि स्क्रीन स्पेस की आवश्यकता की गणना करने के लिए कितना तेज चलता है या कितना ईंधन की आवश्यकता है। ऐसा करने के लिए, हमें वेक्टर वी की लंबाई (मॉड्यूल) खोजने की आवश्यकता है। वेक्टर की लंबाई ऊर्ध्वाधर रेखाओं द्वारा इंगित की जाती है, हमारे मामले में वेक्टर V की लंबाई के रूप में चिह्नित किया जाएगा। V |

हम पक्षों 4 और 3 के साथ एक सही त्रिकोण के रूप में वी का प्रतिनिधित्व कर सकते हैं और, पायथागॉरियन प्रमेय का उपयोग करते हुए, अभिव्यक्ति से कर्ण प्राप्त कर सकते हैं: x ² + y ² = h ²

हमारे मामले में, हमें वर्गाकार रूट (वर्ग ² (x ² + ^{2 2} )) से घटकों (x, y) के साथ वेक्टर H की लंबाई मिलती है।

तो, हमारे जहाज की गति है:

| वी | = sqrt (4 ² + 3 ² ) = sqrt (25) = 5

इस दृष्टिकोण का उपयोग तीन आयामी वैक्टर के लिए भी किया जाता है। घटकों (x, y, z) के साथ वेक्टर की लंबाई की गणना sqrt (x ² + y ² + z ² ) के रूप में की जाती है

दूरी

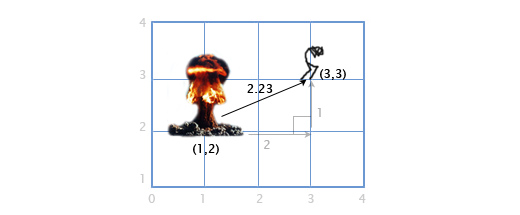
यदि खिलाड़ी P बिंदु (3, 3) पर है, और निर्देशांक (1, 2) द्वारा बिंदु E पर विस्फोट हुआ है, तो हमें खिलाड़ी और विस्फोट के बीच की दूरी को निर्धारित करने की आवश्यकता है ताकि खिलाड़ी को हुए नुकसान की डिग्री की गणना की जा सके। ऊपर वर्णित दो ऑपरेशनों को मिलाकर यह करना आसान है: वैक्टर और उनकी लंबाई घटाना।
हम उनके बीच वेक्टर पाने के लिए P - E को घटाते हैं। और फिर हम इस वेक्टर की लंबाई निर्धारित करते हैं, जो हमें वांछित दूरी प्रदान करता है। ऑपरेंड का क्रम यहां कोई मायने नहीं रखता है। ई - पी | वही परिणाम देगा।

दूरी = | पी - ई | = | (3, 3) - (1, 2) | = | (2, 1) | = sqrt (2 ² +1 ² ) = sqrt (5) = 2.23

मानकीकरण

जब हम दिशाओं (स्थानों और गति के विपरीत) के साथ काम कर रहे हैं, तो यह महत्वपूर्ण है कि दिशा वेक्टर की लंबाई एक के बराबर हो। यह हमारे जीवन को बहुत सरल करता है। उदाहरण के लिए, मान लें कि एक बंदूक (1, 0) दिशा में तैनात है और 20 मीटर प्रति सेकंड की गति से प्रक्षेप्य को फायर करती है। प्रक्षेप्य के लिए इस मामले में वेग वेक्टर क्या है?

चूंकि दिशा वेक्टर की एकता के बराबर लंबाई है, हम प्रक्षेप्य के वेग से दिशा को गुणा करते हैं और वेग वेक्टर (20, 0) प्राप्त करते हैं। यदि, हालांकि, दिशा वेक्टर की एकता के अलावा एक लंबाई है, तो हम ऐसा नहीं कर सकते। प्रक्षेप्य या तो बहुत तेज़ या बहुत धीमा होगा।

एक वेक्टर जिसकी लंबाई एक के बराबर होती है उसे "सामान्यीकृत" कहा जाता है। वेक्टर को सामान्य कैसे बनाया जाए? बहुत ही सरल। हम वेक्टर के प्रत्येक घटक को उसकी लंबाई से विभाजित करते हैं। यदि, उदाहरण के लिए, हम वेक्टर वी को घटकों (3, 4) के साथ सामान्य करना चाहते हैं, तो हम बस प्रत्येक घटक को उसकी लंबाई से विभाजित करते हैं, अर्थात 5 से, और हम प्राप्त करते हैं (3/5, 4/5)। अब, पाइथागोरस प्रमेय का उपयोग करते हुए, हम यह सुनिश्चित करेंगे कि इसकी लंबाई एकता के बराबर हो:

(३/५) ^२ + (४/५) ^२ = ९ / २५ + १६/२५ = २५/२५ = १

वैक्टर का स्केलर उत्पाद

अदिश उत्पाद क्या है (• के रूप में लिखा है)? दो वैक्टर के स्केलर उत्पाद की गणना करने के लिए, हमें उनके घटकों को गुणा करना होगा, और फिर परिणामों को एक साथ जोड़ना होगा

(a1, a2) • (b1, b2) = a1b1 + a2b2

उदाहरण के लिए: (3, 2) • (1, 4) = 3 * 1 + 2 * 4 = 11. पहली नज़र में यह बेकार लगता है, लेकिन इस पर एक करीब से नज़र डालें:

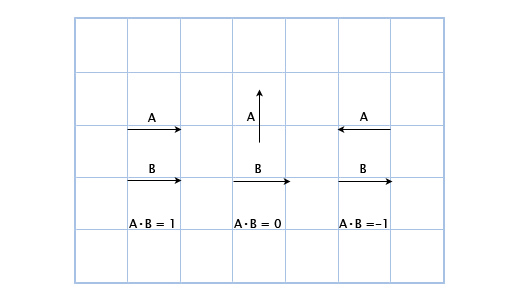
यहां हम देख सकते हैं कि यदि वैक्टर एक दिशा में इंगित करते हैं, तो उनका स्केलर उत्पाद शून्य से अधिक है। जब वे एक दूसरे के लंबवत होते हैं, तो स्केलर उत्पाद शून्य होता है। और जब वे विपरीत दिशाओं में इंगित करते हैं, तो उनका स्केलर उत्पाद शून्य से कम होता है।
असल में, वैक्टर के स्केलर उत्पाद का उपयोग करके, आप गणना कर सकते हैं कि उनमें से कितने एक दिशा में इंगित करते हैं। और यद्यपि यह स्केलर उत्पाद की संभावनाओं का केवल एक छोटा सा हिस्सा है, लेकिन यह हमारे लिए पहले से ही बहुत उपयोगी है।

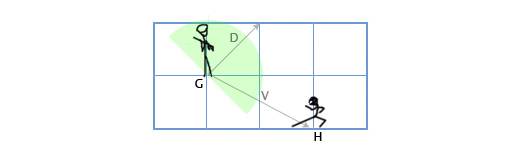
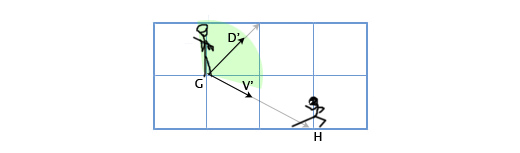
मान लीजिए कि हमारे पास G (1, 3) में स्थित एक गार्ड है जो 180 डिग्री के देखने के कोण के साथ दिशा D (1,1) में देख रहा है। खेल का मुख्य चरित्र एच (3, 2) की स्थिति से उस पर जासूसी करता है। यह कैसे निर्धारित किया जाए कि नायक गार्ड की दृष्टि के क्षेत्र में है या नहीं? हम वैक्टर डी और वी (गार्ड से मुख्य चरित्र के लिए निर्देशित एक वेक्टर) के स्केलर उत्पाद के माध्यम से ऐसा करेंगे। हम निम्नलिखित प्राप्त करते हैं:

वी = एच - जी = (3, 2) - (1, 3) = (3-1, 2-3) = (2, -1)
डी • वी = (1, 1) • (2, -1) = 1 * 2 + 1 * -1 = 2-1 = 1

चूंकि इकाई शून्य से अधिक है, इसलिए मुख्य चरित्र गार्ड की दृष्टि के क्षेत्र में है।

हम पहले से ही जानते हैं कि स्केलर उत्पाद वैक्टर की दिशा निर्धारित करने से संबंधित है। और इसकी अधिक सटीक परिभाषा क्या है? वैक्टर के स्केलर उत्पाद की गणितीय अभिव्यक्ति इस तरह दिखती है:

A • B = | A || B | cosΘ

जहाँ Where (उच्चारण "थीटा") वैक्टर A और B के बीच का कोण है।

यह हमें अभिव्यक्ति का उपयोग करके Θ (कोण) खोजने की अनुमति देता है:

Θ = एकोस ([एबी] / [| ए || बी |])

जैसा कि मैंने पहले कहा था, वैक्टर का सामान्यीकरण हमारे जीवन को सरल बनाता है। और यदि A और B को सामान्यीकृत किया जाता है, तो अभिव्यक्ति इस प्रकार सरल हो जाती है:

Θ = एसीस (एबी)

आइए फिर से गार्ड के परिदृश्य को देखें। बता दें कि अब गार्ड का एंगल 120 डिग्री के बराबर होगा। हम गार्ड (डी ') की निगरानी के लिए और गार्ड से मुख्य चरित्र (वी') के लिए सामान्यीकृत वैक्टर प्राप्त करते हैं। फिर हम उनके बीच के कोण को निर्धारित करते हैं। यदि कोण 60 डिग्री (देखने के कोण का आधा) से अधिक है, तो नायक गार्ड की दृष्टि से बाहर है।

D '= D / | D | = (1, 1) / sqrt (1 ² + 1 ² ) = (1, 1) / sqrt (2) = (0.71, 0.71)
V '= V / | V | = (2, -1) / sqrt (2 ² + (-1) ² ) = (2, -1) / sqrt (5) = (0.89, -0.45)

Θ = एकड़ (D'V ') = एकड़ (0.71 * 0.89 + 0.71 * (- 0.45)) = एकड़ (0.31) = 72

गार्ड के दृष्टि क्षेत्र और नायक के स्थान के बीच का कोण 72 डिग्री है, इसलिए गार्ड उसे नहीं देखता है।

मैं समझता हूं कि यह जटिल लगता है, लेकिन यह इसलिए है क्योंकि हम सब कुछ मैन्युअल रूप से करते हैं। कार्यक्रम में, यह सब बहुत सरल है। निम्नलिखित दिखाता है कि मैंने अपने ओवरग्राउथ गेम में सी ++ वेक्टर पुस्तकालयों का उपयोग करके कैसे किया था जो मैंने लिखा था:

//  vec2 guard_pos = vec2(1,3); vec2 guard_facing = vec2(1,1); vec2 hero_pos = vec2(3,2); //   vec2 guard_facing_n = normalize(guard_facing); vec2 guard_to_hero = normalize(hero_pos - guard_pos); //  float angle = acos(dot(guard_facing_n, guard_to_hero));

वेक्टर कलाकृति

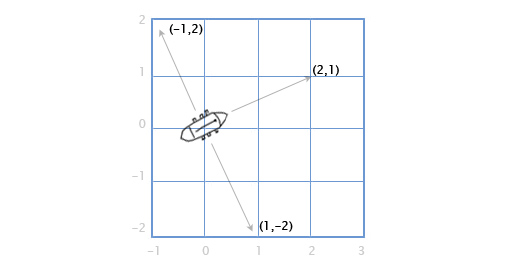
मान लीजिए कि हमारे पास तोपों के साथ एक जहाज है जो पाठ्यक्रम के दाएं और बाएं तरफ शूट करता है। मान लें कि नाव दिशा वेक्टर (2, 1) के साथ स्थित है। अब किस दिशा में बंदूकें चल रही हैं?

यह दो-आयामी ग्राफिक्स में काफी सरल है। दिशा को 90 डिग्री पर दक्षिणावर्त घुमाने के लिए, बस वेक्टर के घटकों को स्वैप करें, और फिर दूसरे घटक के संकेत को बदलें।
(ए, बी) में बदल जाता है (बी, -ए)। इसलिए, वेक्टर (2, 1) के साथ स्थित जहाज पर, स्टारबोर्ड की तरफ की बंदूकें दिशा (1, -2) में गोली मारेंगी, और बंदरगाह की तरफ की बंदूकें विपरीत दिशा में शूट करेंगी। हम वेक्टर के घटकों के संकेतों को बदलते हैं और प्राप्त करते हैं (-1, 2)।

लेकिन क्या होगा अगर हम तीन आयामी ग्राफिक्स के लिए यह सब गणना करना चाहते हैं? जहाज के उदाहरण पर विचार करें।
हमारे पास मस्तूल वेक्टर M है जो सीधे (0, 1, 0) और हवा की दिशा: उत्तर-उत्तर-पूर्व W (1, 0, 2) को निर्देशित करता है। और हम सबसे अच्छे तरीके से "हवा को पकड़ने" के लिए, पाल एस की दिशा वेक्टर की गणना करना चाहते हैं।

इस समस्या को हल करने के लिए, हम वेक्टर उत्पाद का उपयोग करते हैं: एस = एम एक्स डब्ल्यू।

A ( ₁ , ₂ , ₃ ) और B (b ₁ , b ₂ , b ₃ ) का वेक्टर उत्पाद समान होगा:

(एक ₂ बी ₃ -ए ₃ बी ₂ , एक ₃ बी ₁ -ए ₁ बी ₃ , एक ₁ बी ₂ -ए ₂ बी ₁ )

अब हम उन मूल्यों को प्रतिस्थापित करेंगे जिनकी हमें आवश्यकता है:

S = MxW = (0, 1, 0) x (1, 0, 2) = ([1 * 2 - 0 * 0], [0 * 1 - 0 * 2], [0 * 0 - 1 * 1] ) = (2, 0, -1)

मैन्युअल गणनाओं के लिए, यह काफी कठिन है, लेकिन ग्राफ़िकल और गेमिंग अनुप्रयोगों के लिए, मैं नीचे दिए गए संकेत के समान एक फ़ंक्शन लिखने की सलाह देता हूं और अब ऐसी गणनाओं के विवरण में नहीं जाना चाहिए।

 vec3 cross(vec3 a, vec3 b) { vec3 result; result[0] = a[1] * b[2] - a[2] * b[1]; result[1] = a[2] * b[0] - a[0] * b[2]; result[2] = a[0] * b[1] - a[1] * b[0]; return result; }

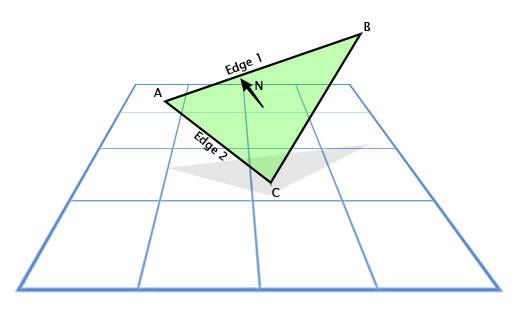
सतह के मानदंडों की गणना करने के लिए एक वेक्टर उत्पाद अक्सर खेलों में उपयोग किया जाता है। दिशाएँ जिसमें यह या वह सतह "दिखता है"। उदाहरण के लिए, वर्टिकल A, B और C. के वैक्टर के साथ एक त्रिभुज पर विचार करें। हम उस दिशा को कैसे खोजते हैं जिसमें त्रिभुज "दिखता है", यानी दिशा अपने तल पर लंबवत है? यह जटिल लगता है, लेकिन हमारे पास इस समस्या को हल करने के लिए एक उपकरण है।

हम ए से सी (सी - ए) से दिशा निर्धारित करने के लिए घटाव का उपयोग करते हैं, इसे "फेस 1" (एज 1) और ए से बी (बी - ए) की दिशा निर्धारित करते हैं, इसे "फेस 2" (एज 2) होने दें। । और फिर हम वेक्टर उत्पाद को उन दोनों के लिए लंबवत खोजने के लिए लागू करते हैं, अर्थात्, त्रिकोण के विमान के लंबवत, जिसे "विमान को सामान्य" भी कहा जाता है।

यह कोड में कैसा दिखता है:

 vec3 GetTriangleNormal(vec3 a, vec3 b, vec3 c) { vec3 edge1 = ba; vec3 edge2 = ca; vec3 normal = cross(edge1,edge2); return normal; }

खेलों में, रोशनी की मुख्य अभिव्यक्ति एन • एल के रूप में लिखी जाती है, जहां एन रोशन सतह के लिए सामान्य है, और एल प्रकाश की सामान्यीकृत दिशा वेक्टर है। नतीजतन, सतह उज्ज्वल दिखती है जब प्रकाश सीधे उस पर गिरता है, और अंधेरा जब यह नहीं होता है।

अब हम गेम डेवलपर्स के लिए "परिवर्तन मैट्रिक्स" (परिवर्तन मैट्रिक्स) के रूप में इस तरह के एक महत्वपूर्ण अवधारणा पर विचार करते हैं।

शुरू करने के लिए, हम परिवर्तन मैट्रिक्स के "बिल्डिंग ब्लॉक्स" का अध्ययन करेंगे।

बेस वेक्टर

मान लीजिए कि हम बहुत पुराने हार्डवेयर पर क्षुद्रग्रह खेल लिख रहे हैं और हमें एक सरल द्वि-आयामी अंतरिक्ष यान की आवश्यकता है जो स्वतंत्र रूप से अपने विमान में घूम सकता है। जहाज मॉडल इस तरह दिखता है:

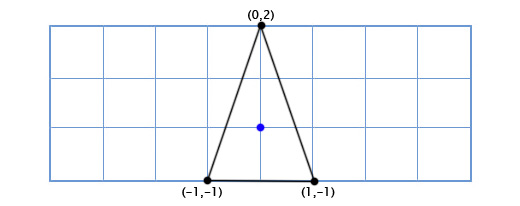
जब कोई खिलाड़ी इसे मनमाने तरीके से डिग्री में बदल देता है, तो हम 49 डिग्री के वामावर्त में जहाज कैसे खींचते हैं। त्रिकोणमिति का उपयोग करते हुए, हम एक दो-आयामी रोटेशन फ़ंक्शन लिख सकते हैं जो बिंदु के निर्देशांक और रोटेशन के कोण को लेता है, और ऑफसेट बिंदु के निर्देशांक लौटाता है:

 vec2 rotate(vec2 point, float angle){ vec2 rotated_point; rotated_point.x = point.x * cos(angle) - point.y * sin(angle); rotated_point.y = point.x * sin(angle) + point.y * cos(angle); return rotated_point; }

इस फ़ंक्शन को सभी तीन बिंदुओं पर लागू करते हुए, हमें निम्न चित्र मिलता है:

साइन और कॉशन के साथ संचालन धीरे-धीरे काम करता है, लेकिन चूंकि हम केवल तीन बिंदुओं के लिए गणना करते हैं, यह पुराने हार्डवेयर पर भी ठीक काम करेगा ( अनुवादक का ध्यान दें: ऐसे मामलों में जहां त्रिकोणमितीय कार्यों का गहन उपयोग गणनाओं को गति देने के लिए किया जाता है, मेमोरी टेबल को प्रत्येक फ़ंक्शन के लिए व्यवस्थित किया जाता है और उस समय की गणना की जाती है जब एप्लिकेशन लॉन्च किया जाता है, फिर जब एक त्रिकोणमितीय फ़ंक्शन की गणना करता है, तो एक टेबल को बस एक्सेस किया जाता है )।

अब हमारे जहाज को इस तरह देखें:

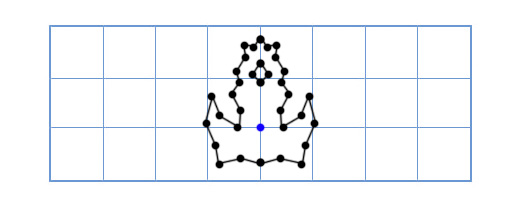
अब पुराना दृष्टिकोण बहुत धीमा हो जाएगा, क्योंकि यह काफी बड़ी संख्या में बिंदुओं को घुमाने के लिए आवश्यक होगा। इस समस्या का एक सुंदर समाधान इस तरह से सुनाई देगा: "क्या होगा यदि जहाज के मॉडल के प्रत्येक बिंदु को मोड़ने के बजाय, हम अपने मॉडल के समन्वय ग्रिड को चालू करते हैं?"

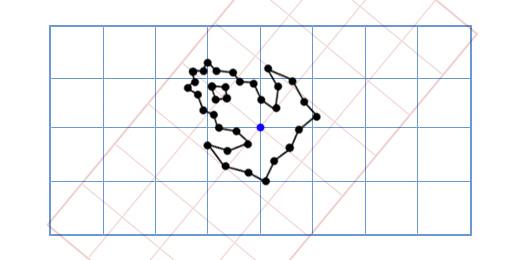
यह कैसे काम करता है? आइए निर्देशांक क्या हैं, इस पर करीब से नज़र डालते हैं।
जब हम निर्देशांक (3, 2) के साथ एक बिंदु के बारे में बात करते हैं, तो हम कहते हैं कि इसका स्थान X समन्वय अक्ष के साथ संदर्भ बिंदु से तीन कदम है, और Y निर्देशांक अक्ष के साथ संदर्भ बिंदु से दो कदम है।

डिफ़ॉल्ट रूप से, समन्वय अक्ष को निम्नानुसार व्यवस्थित किया जाता है: समन्वय अक्ष X (1, 0) के वेक्टर, समन्वय अक्ष Y (0, 1) के वेक्टर। और हमें स्थान मिलता है: 3 (1, 0) + 2 (0, 1)। लेकिन समन्वित कुल्हाड़ियों को उस स्थिति में होना जरूरी नहीं है। यदि हम समन्वय अक्षों को घुमाते हैं, उसी समय हम समन्वय ग्रिड में सभी बिंदुओं को घुमाएंगे।

घुमाए गए कुल्हाड़ियों एक्स और वाई प्राप्त करने के लिए, हम त्रिकोणमितीय कार्यों का उपयोग करते हैं जो ऊपर उल्लिखित थे। यदि हम 49 डिग्री तक घूमते हैं, तो नया समन्वय अक्ष X वेक्टर (0, 1) को 49 डिग्री से घुमाकर प्राप्त किया जाएगा, और नया समन्वय अक्ष Y को वेक्टर (0, 1) को 49 डिग्री से घुमाकर प्राप्त किया जाएगा। तो नए अक्ष X का वेक्टर (0.66, 0.75) के बराबर होगा, और नए अक्ष Y का वेक्टर (-0.75, 0.66) होगा। आइए इसे अपने सरल तीन-बिंदु मॉडल के लिए मैन्युअल रूप से करें ताकि यह सुनिश्चित हो सके कि यह काम करना चाहिए:

शीर्ष बिंदु के निर्देशांक (0, 2) हैं, जिसका अर्थ है कि इसका नया स्थान 0 पर नया (घुमाया) X अक्ष पर और 2 नए Y अक्ष पर है:

0 * (0.66.0.75) + 2 * ((0.75, 0.66) = (-1.5, 1.3)

नीचे का बायां बिंदु (-1, -1) है, जिसका अर्थ है कि इसका नया स्थान -1 घुमाए गए एक्स-अक्ष पर, और -1 घुमाए गए Y- अक्ष पर है:

-1 * (0.66.0.75) + -1 * ((0.75, 0.66) = (0.1, -1.4)

नीचे दाईं ओर बिंदु (1, -1) है, जिसका अर्थ है कि इसका नया स्थान घुमाए गए X अक्ष पर 1 पर है, और घूर्णन Y अक्ष पर -1 है

1 * (0.66.0.75) + -1 * ((0.75, 0.66) = (1.4, 0.1)

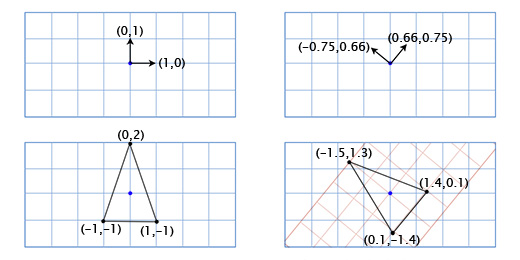
हमने दिखाया कि कैसे जहाज के निर्देशांक एक अन्य समन्वित ग्रिड में घुमाए गए अक्षों (या "बेस वैक्टर") के साथ प्रदर्शित होते हैं। यह हमारे मामले में सुविधाजनक है, क्योंकि यह हमें जहाज मॉडल के प्रत्येक बिंदु पर त्रिकोणमितीय परिवर्तनों को लागू करने से बचाता है।

हर बार जब हम आधार वैक्टर (1, 0) और (0, 1) से (ए, बी) और (सी, डी) में परिवर्तन करते हैं, तो बिंदु (x, y) के नए समन्वय को अभिव्यक्ति का उपयोग करके पाया जा सकता है:

x (a, b) + y (c, d)

आमतौर पर आधार वेक्टर होते हैं (1, 0) और (0, 1) और हम सिर्फ x (1, 0) + y (0, 1) = (x, y) प्राप्त करते हैं, और इसके आगे ध्यान रखने की कोई आवश्यकता नहीं है। हालांकि, यह याद रखना महत्वपूर्ण है कि जब हम इसकी आवश्यकता होती है तो हम अन्य आधार वैक्टर का उपयोग कर सकते हैं।

मैट्रिक्स

मैट्रिक्स द्वि-आयामी वैक्टर के समान हैं। उदाहरण के लिए, एक विशिष्ट 2x2 मैट्रिक्स इस तरह दिख सकता है:

    [Acbd]

जब आप एक वेक्टर द्वारा एक मैट्रिक्स को गुणा करते हैं, तो आप प्रत्येक पंक्ति के स्केलर उत्पाद को वेक्टर के साथ जोड़ते हैं जिसके द्वारा गुणा होता है। उदाहरण के लिए, यदि हम एक वेक्टर (x, y) द्वारा उपरोक्त मैट्रिक्स को गुणा करते हैं, तो हम प्राप्त करते हैं:

(ए, सी) • (एक्स, वाई) + (बी, डी) • (एक्स, वाई)

अलग तरह से लिखे जाने पर, यह अभिव्यक्ति इस तरह दिखती है:

x (a, b) + y (c, d)

परिचित लगता है, है ना? यह ठीक वैसी ही अभिव्यक्ति है जिसका इस्तेमाल हम आधार वैक्टर को बदलने के लिए करते थे। इसका मतलब है कि 2x2 मैट्रिक्स को दो-आयामी वेक्टर से गुणा करना, हम इस प्रकार आधार वैक्टर को बदलते हैं। उदाहरण के लिए, यदि हम मैट्रिक्स के कॉलम में मानक आधार वैक्टर (1, 0) और (0, 1) सम्मिलित करते हैं, तो हमें मिलेगा:

 [१ ० 
  0 1]

यह पहचान मैट्रिक्स है जो उस प्रभाव का उत्पादन नहीं करता है जो हम संकेतित तटस्थ आधार वैक्टर से उम्मीद कर सकते हैं। अगर, हालांकि, हम आधार वैक्टर को 49 डिग्री तक घुमाते हैं, तो हम प्राप्त करते हैं:

 [०.६६-०. 0.५ 
  0.75 0.66]

यह मैट्रिक्स दो आयामी वेक्टर को 49 डिग्री वामावर्त घुमाएगा। हम अपने Asteriods गेम के लिए कोड को इस तरह से मैट्रिसेस का उपयोग करके अधिक सुरुचिपूर्ण बना सकते हैं। उदाहरण के लिए, हमारे जहाज का रोटेशन फंक्शन इस तरह दिख सकता है:

 void RotateShip(float degrees){ Matrix2x2 R = GetRotationMatrix(degrees); for(int i=0; i<num_points; ++i){ rotated_point[i] = R * point[i]; } }

हालाँकि, हमारा कोड और भी अधिक सुरुचिपूर्ण होगा यदि हम इस मैट्रिक्स को अंतरिक्ष में जहाज की आवाजाही में शामिल कर सकते हैं। फिर हमारे पास एक एकल डेटा संरचना होगी जिसमें ऑब्जेक्ट के उन्मुखीकरण और अंतरिक्ष में इसके स्थान के बारे में जानकारी शामिल होगी।

सौभाग्य से, इसे प्राप्त करने का एक तरीका है, हालांकि यह बहुत सुरुचिपूर्ण नहीं दिखता है। यदि हम वेक्टर (ई, एफ) का उपयोग करना चाहते हैं, तो हम इसे केवल अपने परिवर्तन मैट्रिक्स में शामिल करते हैं:

 [acebdf 0 0 1]

और हम प्रत्येक वेक्टर के अंत में एक अतिरिक्त इकाई जोड़ते हैं जो ऑब्जेक्ट के स्थान को निर्धारित करता है, उदाहरण के लिए:

[xy 1]

अब, जब हम उन्हें गुणा करते हैं, तो हम प्राप्त करते हैं:

(ए, सी, ई) • (एक्स, वाई, 1) + (बी, डी, एफ) • (एक्स, वाई, 1) + (0, 0, 1) • (एक्स, वाई, 1)

जो, बदले में, के रूप में लिखा जा सकता है:

x (a, b) + y (c, d) + (e, f)

अब हमारे पास एक मैट्रिक्स में संलग्न पूर्ण रूपांतरण तंत्र है। यह महत्वपूर्ण है यदि आप कोड की लालित्य को ध्यान में नहीं रखते हैं, क्योंकि इसके साथ अब हम सभी मानक मैट्रिक्स जोड़तोड़ का उपयोग कर सकते हैं। उदाहरण के लिए, वांछित प्रभाव जोड़ने के लिए मैट्रिसेस को गुणा करें, या हम ऑब्जेक्ट की सटीक विपरीत स्थिति प्राप्त करने के लिए मैट्रिक्स को उल्टा कर सकते हैं।

3 डी मेट्रिक्स

त्रि-आयामी अंतरिक्ष में मेट्रिक्स दो-आयामी में समान कार्य करते हैं। मैंने द्वि-आयामी वैक्टर और मैट्रिस के साथ उदाहरण दिए, क्योंकि वे एक दो-आयामी चित्र दिखाने वाले डिस्प्ले का उपयोग करके प्रदर्शित करना आसान है। हमें बस दो के बजाय आधार वैक्टर के लिए तीन कॉलम को परिभाषित करने की आवश्यकता है। यदि आधार वैक्टर (ए, बी, सी), (डी, ई, एफ) और (जी, एच, आई) हैं, तो हमारा मैट्रिक्स इस तरह दिखेगा:

 [Adgbehcfi]

यदि हमें स्थानांतरित करने की आवश्यकता है (जे, के, एल), तो हम एक अतिरिक्त कॉलम और पंक्ति जोड़ते हैं, जैसा कि उन्होंने पहले कहा था:

 [adgjbehkcfil 0 0 0 1]

और वेक्टर में यूनिट [1] को यहां जोड़ें:

[xyz 1]

द्वि-आयामी रोटेशन

चूंकि हमारे मामले में हमारे पास केवल एक रोटेशन अक्ष (प्रदर्शन पर स्थित) है, केवल एक चीज जिसे हमें जानना आवश्यक है वह है कोण। मैंने पहले इस बारे में बात की थी, जिसका उल्लेख करते हुए कि हम इस तरह के द्वि-आयामी रोटेशन कार्यों को लागू करने के लिए त्रिकोणमितीय कार्यों का उपयोग कर सकते हैं:

 vec2 rotate(vec2 point, float angle){ vec2 rotated_point; rotated_point.x = point.x * cos(angle) - point.y * sin(angle); rotated_point.y = point.x * sin(angle) + point.y * cos(angle); return rotated_point; }

इसे मैट्रिक्स रूप में अधिक सुरुचिपूर्ण ढंग से व्यक्त किया जा सकता है। मैट्रिक्स का निर्धारण करने के लिए, हम इस फ़ंक्शन को कोण to के लिए कुल्हाड़ियों (1, 0) और (0, 1) पर लागू कर सकते हैं और फिर हमारे मैट्रिक्स के कॉलम में परिणामी अक्षों को शामिल कर सकते हैं। तो, चलो समन्वय अक्ष X (1, 0) से शुरू करते हैं। यदि हम अपने कार्य को उस पर लागू करते हैं, तो हम प्राप्त करते हैं:

(1 * cos (Θ) - 0 * sin (,), 1 * sin (cos) + 0 * cos (() = = (cos (Θ), sin (Θ))

फिर, हम समन्वय अक्ष Y (0, 1) को शामिल करते हैं। हमें मिलता है:

(0 * cos (Θ) - 1 * sin (,), 0 * sin (cos) + 1 * cos (()) = (-sin (,), cos (Θ))

हम मैट्रिक्स में प्राप्त समन्वित कुल्हाड़ियों को शामिल करते हैं, और हम दो आयामी रोटेशन मैट्रिक्स प्राप्त करते हैं:

 [cos ([) -sin (() 
  sin (Θ) cos (Θ)]

इस मैट्रिक्स को सुसनाह में लागू करें, ब्लेंडर ग्राफिक्स पैकेज से बंदर। रोटेशन का कोण 45 45 डिग्री दक्षिणावर्त है।

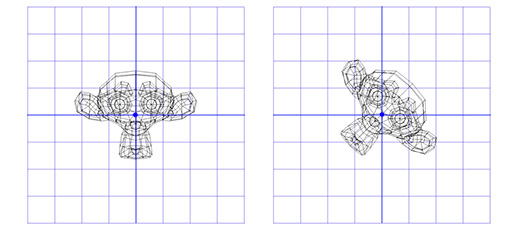
जैसा कि आप देख सकते हैं, यह काम करता है। लेकिन क्या होगा अगर हमें (0, 0) के अलावा किसी बिंदु पर घूमने की आवश्यकता हो?
उदाहरण के लिए, हम बंदर के सिर को उसके कान में स्थित बिंदु के चारों ओर घुमाना चाहते हैं:

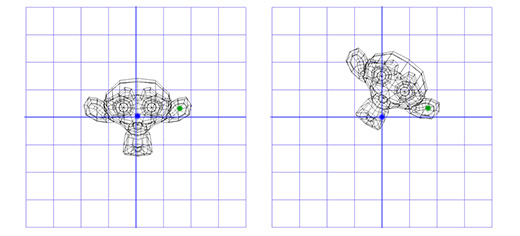
ऐसा करने के लिए, हम एक अनुवाद मैट्रिक्स टी बनाकर शुरू कर सकते हैं, जो ऑब्जेक्ट को शुरुआती बिंदु से बंदर के कान में रोटेशन बिंदु तक ले जाता है, और रोटेशन मैट्रिक्स आर, प्रारंभिक बिंदु के चारों ओर ऑब्जेक्ट को घुमाने के लिए। अब, कान में स्थित एक बिंदु के चारों ओर घूमने के लिए, हम सबसे पहले कान में शुरुआती बिंदु की जगह पर ले जा सकते हैं, टी ^{-1 के} रूप में लिखे मैट्रिक्स टी को इन्वर्ट करके। फिर, हम मैट्रिक्स आर का उपयोग करके शुरुआती बिंदु के चारों ओर ऑब्जेक्ट को घुमाते हैं, और फिर रोटेशन बिंदु को अपनी मूल स्थिति में वापस लाने के लिए मैट्रिक्स टी को लागू करते हैं।
नीचे वर्णित चरणों में से प्रत्येक का एक चित्रण है:

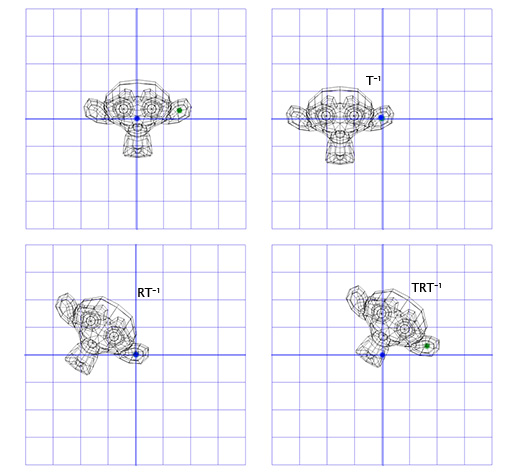
यह एक महत्वपूर्ण टेम्प्लेट है जिसे हम बाद में लागू करेंगे - दो विपरीत परिवर्तनों के लिए रोटेशन का उपयोग हमें ऑब्जेक्ट को दूसरे "स्पेस" में घुमाने की अनुमति देता है। जो बहुत सुविधाजनक और उपयोगी है।

अब तीन आयामी रोटेशन पर विचार करें।

3 डी रोटेशन

Z अक्ष के चारों ओर घूर्णन दो-आयामी अंतरिक्ष में रोटेशन के समान सिद्धांत पर काम करता है। हमें केवल एक अतिरिक्त कॉलम और पंक्ति जोड़कर अपने पुराने मैट्रिक्स को बदलना होगा:

 [cos (0) -sin (() ० 
  sin (cos) cos (cos) ० 
  0 0 1]

हम इस मैट्रिक्स को सुज़ाना के तीन आयामी संस्करण पर लागू करते हैं, ब्लेंडर पैकेज से बंदर। रोटेशन कोण Θ 45 डिग्री के दक्षिणावर्त के बराबर होना चाहिए।

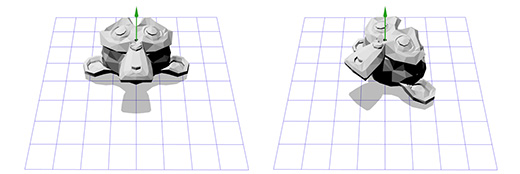
वही बात। केवल Z अक्ष के चारों ओर घूमना हमें सीमित करता है, एक मनमानी अक्ष के चारों ओर घूमने के बारे में कैसे?

एक्सिस-कोण रोटेशन

अक्ष और कोण द्वारा परिभाषित रोटेशन का प्रतिनिधित्व घातीय निर्देशांक में रोटेशन के रूप में भी जाना जाता है, दो मात्राओं के रोटेशन द्वारा पैरामीटर। एक वेक्टर जो गाइड अक्ष के रोटेशन (सीधी रेखा) और एक कोण को परिभाषित करता है जो इस अक्ष के चारों ओर रोटेशन की मात्रा का वर्णन करता है। दाहिने हाथ के नियम के अनुसार रोटेशन किया जाता है।

तो, रोटेशन को दो मापदंडों (अक्ष, कोण) द्वारा परिभाषित किया गया है, जहां अक्ष रोटेशन के अक्ष का वेक्टर है, और कोण रोटेशन का कोण है। यह तकनीक काफी सरल है और कई अन्य रोटेशन ऑपरेशंस के लिए एक शुरुआती बिंदु प्रदान करता है, जिनके साथ मैं काम करता हूं। अक्ष और कोण द्वारा निर्धारित रोटेशन को व्यावहारिक रूप से कैसे लागू करें?

मान लें कि हम रोटेशन की धुरी के साथ काम कर रहे हैं, नीचे दिए गए चित्र में दिखाया गया है:

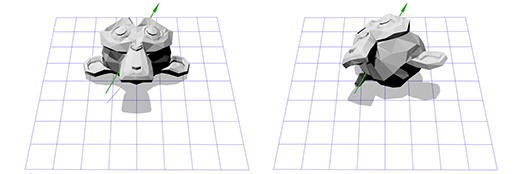
हम Z अक्ष के चारों ओर किसी वस्तु को घुमाना जानते हैं, और हम जानते हैं कि किसी वस्तु को अन्य स्थानों में कैसे घुमाना है। तो, हमें बस एक ऐसी जगह बनाने की जरूरत है जहां हमारे रोटेशन की धुरी Z अक्ष होगी। और यदि यह अक्ष Z अक्ष है, तो X और Y अक्ष क्या होगा? अब गणना करते हैं।

नई कुल्हाड़ियों एक्स और वाई बनाने के लिए हमें केवल दो वैक्टर का चयन करना होगा जो नए Z अक्ष के लंबवत और एक दूसरे के लंबवत हों। हम पहले से ही वेक्टर गुणन के बारे में बात कर चुके हैं, जो दो वैक्टर लेता है और एक वेक्टर देता है जो उनके लिए लंबवत है।

हमारे पास अब एक वेक्टर है, यह रोटेशन अक्ष है, इसे ए कहते हैं। अब चलो एक यादृच्छिक अन्य वेक्टर बी लेते हैं, जो वेक्टर ए के समान दिशा में नहीं है। उदाहरण के लिए इसे (0, 0, 1) होने दें।

अब हमारे पास एक घूर्णन अक्ष ए और एक यादृच्छिक वेक्टर बी है, हम वेक्टर उत्पाद ए और बी सी के माध्यम से सामान्य सी प्राप्त कर सकते हैं। ए और बी के लिए लंबवत है। अब हम वेक्टर बी को उनके वेक्टर उत्पाद के लिए लंबवत ए और सी बनाते हैं। और यह हमारे लिए आवश्यक सभी समन्वय अक्ष हैं।

शब्दों में, यह जटिल लगता है, लेकिन यह कोड में या चित्रों में दिखाए जाने पर बहुत सरल लगता है।
निम्नलिखित दिखाता है कि यह कोड में कैसा दिखता है:

 B = (0,0,1); C = cross(A,B); B = cross(C,A);

यहाँ प्रत्येक चरण के लिए एक चित्रण है:

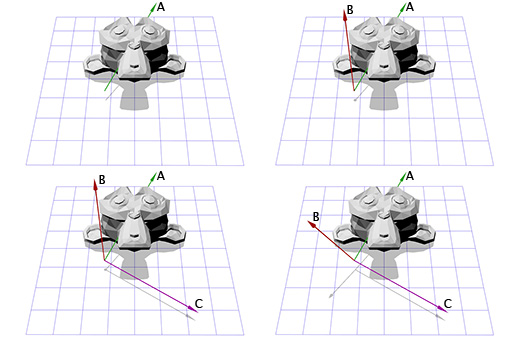
अब जब हमारे पास नए समन्वय अक्षों के बारे में जानकारी है, तो हम इस मैट्रिक्स में एक कॉलम के रूप में प्रत्येक अक्ष को शामिल करके मैट्रिक्स एम की रचना कर सकते हैं। हमें यह सुनिश्चित करने की आवश्यकता है कि वेक्टर ए तीसरा स्तंभ है ताकि यह हमारा नया समन्वय अक्ष Z हो।

 [बी ० सी ० ए ० 
  बी 1 सी 1 ए 1 
  बी 2 सी 2 ए 2]

अब यह वैसा ही है जैसा हमने द्वि-आयामी अंतरिक्ष में घूमने के लिए किया था। हम एक नई निर्देशांक प्रणाली में जाने के लिए उल्टे मैट्रिक्स M का उपयोग कर सकते हैं, फिर Z अक्ष के चारों ओर ऑब्जेक्ट को घुमाने के लिए मैट्रिक्स R के अनुसार घुमा सकते हैं, फिर मूल समन्वय स्थान पर लौटने के लिए मैट्रिक्स M को लागू कर सकते हैं।

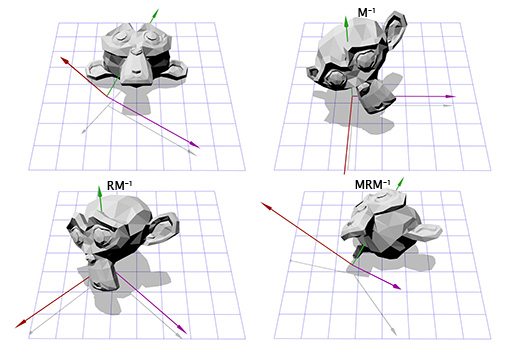
अब हम ऑब्जेक्ट को एक मनमाना अक्ष के चारों ओर घुमा सकते हैं। अंत में, हम केवल मैट्रिक्स टी = टी = एम ^-1 आरएम बना सकते हैं और इसे कई बार उपयोग कर सकते हैं, बिना हमारी ओर से कोई अतिरिक्त प्रयास किए। मैट्रिक्स और कोणों द्वारा परिभाषित घुमावों को मैट्रिक्स द्वारा परिभाषित घुमावों में परिवर्तित करने के अधिक कुशल तरीके हैं। हमारे द्वारा बताए गए दृष्टिकोण से पता चलता है कि हमने पहले क्या बात की थी।

अक्ष और कोण द्वारा परिभाषित रोटेशन शायद सबसे सहज तरीका है। इसका उपयोग करना, कोने पर संकेत बदलकर रोटेशन को उल्टा करना बहुत आसान है, और कोण को प्रक्षेपित करके प्रक्षेपित करना आसान है। हालांकि, एक गंभीर सीमा है, और यह इस तथ्य में निहित है कि इस तरह के रोटेशन एक योग नहीं है। अर्थात्, आप अक्ष और कोण द्वारा परिभाषित दो घूर्णन को जोड़ नहीं सकते।
अक्ष और कोण द्वारा परिभाषित रोटेशन शुरू करने का एक अच्छा तरीका है, लेकिन इसे और अधिक जटिल मामलों में उपयोग किए जाने के लिए कुछ और में परिवर्तित किया जाना चाहिए।

यूलर कोण

एयुलर एंगल्स रोटेशन के दूसरे तरीके का प्रतिनिधित्व करते हैं, जिसमें एक्स, वाई और जेड एक्सिस के सापेक्ष तीन नेस्टेड घुमाव शामिल हैं। आप उन खेलों में उनके उपयोग का सामना कर सकते हैं जहां कैमरा पहले व्यक्ति में या तीसरे व्यक्ति में कार्रवाई दिखाता है।

मान लीजिए कि आप पहले व्यक्ति का शूटर खेलते हैं और आपने बाईं ओर 30 डिग्री घुमाया, और फिर 40 डिग्री तक देखा। अंत में, वे आप पर गोली मारते हैं, आपको मारते हैं, और झटका के परिणामस्वरूप, कैमरा अपनी धुरी पर 45 डिग्री से घूमता है। यूलर एंगल्स (30, 40, 45) का उपयोग करके रोटेशन को नीचे दिखाया गया है।

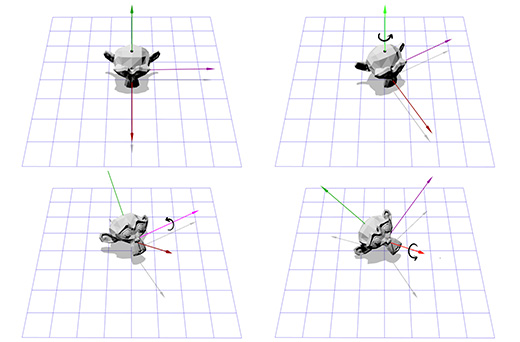
यूलर एंगल्स एक सुविधाजनक और उपयोग में आसान उपकरण है। लेकिन इस विधि में दो कमियां हैं।

पहले एक स्थिति की संभावना है जिसे "अक्ष लॉक" या "जिम्बल लॉक" कहा जाता है । पहले व्यक्ति के शूटर को खेलने की कल्पना करें जहां आप बाएं, दाएं, ऊपर और नीचे देख सकते हैं, या दृश्य अक्ष के चारों ओर कैमरा घुमा सकते हैं। अब कल्पना करें कि आप सीधे ऊपर देख रहे हैं। इस स्थिति में, बाएं या दाएं देखने की कोशिश कैमरे को घुमाने की कोशिश के समान होगी। इस मामले में हम जो कुछ भी कर सकते हैं, वह है कि आप अपनी धुरी के चारों ओर कैमरा घुमाएँ, या नीचे देखें। जैसा कि आप कल्पना कर सकते हैं, यह सीमा उड़ान सिमुलेटरों में यूलर कोणों का उपयोग करने के लिए अव्यावहारिक है।

रोटेशन के दो यूलर कोणों के बीच दूसरा - प्रक्षेप उनके बीच सबसे छोटा रास्ता नहीं देता है।
उदाहरण के लिए, आपके पास दो समान घुमावों के बीच दो प्रक्षेप हैं। पहला Eulerian angle प्रक्षेप का उपयोग करता है, दूसरा सबसे छोटा रास्ता खोजने के लिए गोलाकार रैखिक प्रक्षेप (SLERP) का उपयोग करता है।

तो, रोटेशन को प्रक्षेपित करने के लिए अधिक उपयुक्त क्या है? शायद मेट्रिसेस?

मैट्रिक्स रोटेशन

जैसा कि हमने पहले कहा था, रोटेशन मेट्रिक्स तीन अक्षों के बारे में जानकारी संग्रहीत करते हैं। इसका मतलब है कि दो मैट्रिक्स के बीच प्रक्षेप केवल प्रत्येक अक्ष को रैखिक रूप से प्रक्षेपित करता है। नतीजतन, यह हमें एक प्रभावी तरीका देता है, यह नई समस्याओं का भी परिचय देता है। उदाहरण के लिए, दो घुमाव और एक प्रक्षेपित अर्ध-घुमाव यहां दिखाए गए हैं: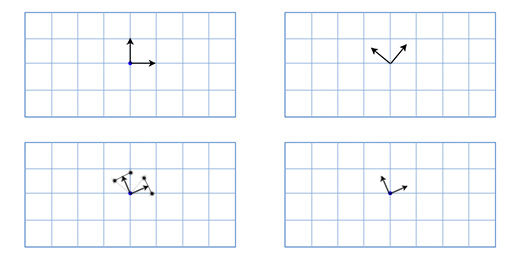

जैसा कि आप देख सकते हैं, प्रक्षेपित घुमाव किसी भी मूल घुमाव की तुलना में बहुत छोटा है, और दो अक्ष अब एक दूसरे के लंबवत नहीं हैं। यह तर्कसंगत है, अगर आप इसके बारे में सोचते हैं - क्षेत्र के मध्य में किसी भी दो बिंदुओं को जोड़ने वाले क्षेत्र के मध्य क्षेत्र के केंद्र के करीब स्थित होगा।

यह बदले में कंकाल एनीमेशन का उपयोग करते समय प्रसिद्ध कैंडी आवरण प्रभाव को जन्म देता है। नीचे हमारे अतिवृद्धि खेल से खरगोश के उदाहरण का उपयोग करके इस आशय का एक प्रदर्शन है।( नोट अनुवादक: खरगोश के शरीर के मध्य भाग पर ध्यान दें )।

मैट्रिक्स ऑपरेशन पर आधारित रोटेशन बहुत उपयोगी है, क्योंकि वे बिना किसी समस्या के रोटेशन को जमा कर सकते हैं, जैसे कि जिम्बल लॉक, और दृश्य में बिंदुओं पर बहुत प्रभावी ढंग से लागू किया जा सकता है। यही कारण है कि मैट्रिक्स रोटेशन समर्थन ग्राफिक्स कार्ड में बनाया गया है। किसी भी प्रकार के त्रि-आयामी ग्राफिक्स के लिए, मैट्रिक्स रोटेशन प्रारूप हमेशा अंतिम लागू विधि है।

हालांकि, जैसा कि हम पहले से ही जानते हैं, मैट्रिस बहुत अच्छी तरह से प्रक्षेपित नहीं हैं, और वे इतने सहज नहीं हैं।

तो, केवल एक मुख्य रोटेशन प्रारूप बचा है। अंतिम, लेकिन फिर भी महत्वपूर्ण है।

quaternions

चतुर्धातुक क्या हैं? संक्षेप में, यह अक्ष-कोण (अक्ष-कोण रोटेशन) के आधार पर एक वैकल्पिक घुमाव है जो अंतरिक्ष में मौजूद है।

मैट्रिसेस की तरह, वे घुमावों को जमा कर सकते हैं, अर्थात्, आप उनसे रोटेशन की एक श्रृंखला बना सकते हैं, बिना किसी डर के, जिम्बल लॉक प्राप्त कर सकते हैं। और एक ही समय में, मैट्रिस के विपरीत, उन्हें एक स्थिति से दूसरे स्थान पर अच्छी तरह से प्रक्षेपित किया जा सकता है।

क्या चतुर्भुज अन्य रोटेशन स्वरूपों की तुलना में बेहतर समाधान हैं?
आज वे अन्य रोटेशन विधियों की सभी शक्तियों को जोड़ते हैं। लेकिन उनकी दो कमजोरियां हैं, जिनकी जांच की गई है, हम इस निष्कर्ष पर पहुंचे हैं कि मध्यवर्ती रोटेशन के लिए quaternions का सबसे अच्छा उपयोग किया जाता है। तो क्या खदानों के नुकसान हैं।

सबसे पहले, चतुर्भुज को त्रि-आयामी अंतरिक्ष में प्रदर्शित करना आसान नहीं है। और हम रोटेशन को हमेशा सरल तरीके से लागू करने के लिए मजबूर होते हैं, और फिर इसे परिवर्तित करते हैं। दूसरे, quaternions प्रभावी ढंग से अंक नहीं घुमा सकते हैं, और हम उन्हें अंकों की एक महत्वपूर्ण संख्या को घुमाने के लिए मैट्रिसेस में परिवर्तित करने के लिए मजबूर हैं।

इसका मतलब है कि आप सबसे अधिक संभावना quaternions का उपयोग करके घुमावों की एक श्रृंखला को शुरू या समाप्त नहीं करेंगे। लेकिन उनकी मदद से, किसी भी अन्य दृष्टिकोण की तुलना में मध्यवर्ती घुमाव को अधिक कुशलता से लागू किया जा सकता है।

चतुर्धातुक तंत्र की "आंतरिक रसोई" मेरे लिए बहुत स्पष्ट और दिलचस्प नहीं है। और यह आपके लिए दिलचस्प नहीं हो सकता, जब तक कि आप गणितज्ञ न हों। और मैं आपको उन पुस्तकालयों को खोजने की सलाह देता हूं जो आपकी मदद से आपकी समस्याओं को हल करने के लिए quaternions के साथ काम करते हैं।

बुलेट या ब्लेंडर गणित पुस्तकालय शुरू करने के लिए एक अच्छी जगह है।

गेम डेवलपर्स के लिए रैखिक बीजगणित