अप्रैल-मई 2011 में, यैंडेक्स ने
यैंडेक्स इंटरनेट मठ प्रतियोगिता का एक और दौर आयोजित किया। दौरे का विषय: "छवियों की दृश्य समानता का निर्धारण।"
मैंने
विजेताओं की
घोषणा के बारे में समाचार प्रकाशित किया और जल्द ही हमारी टीम - लुकलाइक द्वारा कार्य के समाधान का वर्णन करने का वादा किया, जिसने अंतिम रेटिंग में 12 वां स्थान प्राप्त किया।
और अब, समय बिल्कुल सही नहीं है!
परिचय
यैंडेक्स इंटरनेट मठ यैंडेक्स द्वारा आयोजित प्रतियोगिताओं की एक श्रृंखला है, जो 2011 में पांचवीं बार आयोजित की गई थी। प्रतियोगिता की मुख्य सामग्री वास्तविक आंकड़ों के आधार पर वास्तविक समस्याओं को हल करने के लिए प्रतिस्पर्धा है। 2011 में प्रतियोगिता के लिए एक कार्य के रूप में, चित्रमाला की एक श्रृंखला में अतिरिक्त फ्रेम निर्धारित करने के लिए छवियों की दृश्य समानता का विश्लेषण चुना गया था। यह लेख समस्या के विवरण, कार्यप्रणाली और इसके समाधान के लिए दृष्टिकोण का वर्णन करेगा, जो हमारे द्वारा प्रतियोगिता के ढांचे में लागू किए गए थे, साथ ही परिणामों का विश्लेषण भी।
प्रतियोगिता के डेटा Yandex.Maps सेवा के मनोरम चित्रों से प्राप्त चित्र थे। प्रतियोगिता को दो चरणों में विभाजित किया गया था - प्रशिक्षण चरण, जिसमें 5 छवियों के 6,000 एपिसोड थे (प्रत्येक छवि आयाम 300x300 पिक्सल था), और अंतिम चरण, जिसमें 5 छवियों के 6,000 एपिसोड का एक और सेट था। प्रत्येक श्रृंखला का आधार आंशिक ओवरलैप (संभवतः गलत क्रम में) के साथ एक पैनोरमा के क्रमिक टुकड़े हैं। कुछ श्रृंखलाओं में अन्य नयनाभिराम श्रृंखलाओं से एक या दो अतिरिक्त शॉट होते हैं। श्रृंखला में अतिरिक्त फ़्रेम निर्धारित करने के लिए प्रतिभागियों का कार्य स्वचालित तरीकों का उपयोग कर रहा था। प्रशिक्षण सेट की 6000 श्रृंखलाओं में से 1000 एक प्रशिक्षण सेट था जिसके लिए यह संकेत दिया गया था कि कौन सी तस्वीरें अनावश्यक थीं।
श्रृंखला के उदाहरण:
प्रतियोगिता पद्धति इस प्रकार थी। टीमों ने इस सवाल का जवाब दिया: प्रशिक्षण चरण में 5000 श्रृंखलाओं के लिए 5 तस्वीरों की प्रत्येक श्रृंखला में कौन सी तस्वीरें बहुत अधिक हैं (1001 से 6000 तक, क्योंकि पहले 1000 श्रृंखलाएं शैक्षिक थीं और उत्तर इसके लिए जाने जाते थे)। यह उत्तर एक पाठ फ़ाइल के रूप में बनाया गया था, जिसने प्रत्येक श्रृंखला के लिए अतिरिक्त चित्रों का संकेत दिया था। इस फ़ाइल के आधार पर, यैंडेक्स सर्वर ने विश्लेषण परिणामों के सार्वजनिक मूल्यांकन की गणना की। अंतिम चरण में, 6,000 पूर्व अज्ञात श्रृंखला का एक सेट प्रस्तावित किया गया था। प्रारंभिक चरण 2 महीने तक चला, अंतिम चरण ठीक एक दिन (16 मई से 17 मई, 2011 तक) रहा।
परिणामों के मूल्यांकन के लिए मुख्य मीट्रिक सही ढंग से वर्गीकृत तस्वीरों का अनुपात है (दो वर्गों पर विचार किया जाता है: ऐसे चित्र जो पैनोरमा और शानदार बनाते हैं)। सूत्र के अनुसार मूल्यांकन किया गया था:
(Tp + Tn) / (P + N), जहां P चित्रमाला से संबंधित छवियों की संख्या है, N अतिरिक्त छवियों की संख्या है, Tp छवियों की संख्या है जो सिस्टम सही तरीके से चित्रमाला को सौंपे गए हैं, Tn उन चित्रों की संख्या है जिन्हें सिस्टम सही ढंग से असाइन किया गया है शानदार वर्ग। इस प्रकार, यदि सिस्टम बिल्कुल सही ढंग से सभी तस्वीरों को पैनोरमा कक्षाओं और शानदार में विभाजित करता है, तो रेटिंग 1 होगी।
मीट्रिक का विश्लेषण करने के बाद, यह स्पष्ट हो जाता है कि एक श्रृंखला में त्रुटि विभिन्न तरीकों से परिणाम के समग्र मूल्यांकन को प्रभावित कर सकती है। चित्र 1 में दिखाई गई श्रृंखला पर विचार करें। यदि सिस्टम कहता है कि 2,3,4,5 चित्र एक ही पैनोरमा में हैं, और 1 एक शानदार है, तो अनुमान होगा (3 + 1) / (3 + 2) = 4/5। यदि सिस्टम यह परिणाम देता है कि 2, 3 और 4 के चित्र एक ही पैनोरमा में हैं, और 1 और 5 अतिरेकपूर्ण हैं, तो अनुमान होगा (1 + 0) / (3 + 2) = 1/5। जैसा कि इससे देखा जा सकता है, कुछ प्रकार की त्रुटियां दूसरों की तुलना में समग्र स्कोर को काफी खराब कर सकती हैं, जिसे सिस्टम को डिज़ाइन करते समय ध्यान में रखा जाना चाहिए।
समस्या को हल करने के लिए एक प्रणाली विकसित करने में मुख्य कार्य मेट्रिक्स को निर्धारित करना था, जिसके आधार पर यह निर्धारित करना संभव है कि क्या दो चित्र एक ही पैनोरमा के हिस्से हैं और एक निर्णय उपतंत्र बनाते हैं, जो इन मैट्रिक्स के आधार पर, प्रत्येक श्रृंखला के लिए परिणामी उत्तर का निर्माण करेगा।
मैट्रिक्स
यह निर्धारित करने के लिए कि क्या दो चित्र एक ही पैनोरमा के हैं, हमने कई प्रकार के मैट्रिक्स विकसित किए हैं जो विभिन्न स्थितियों में उपयोग किए जाते हैं। एक श्रृंखला में छवियों की तुलना जोड़े में की जाती है। आइए इन मैट्रिक्स पर अधिक विस्तार से विचार करें।
1. ओवरले मीट्रिक
समस्या के बयान में यह शर्त है कि एक चित्रमाला से छवियों का आंशिक ओवरलैप होना चाहिए। यह हमेशा मामला नहीं होता है, लेकिन ज्यादातर मामलों में, वास्तव में, ओवरलैप हुआ है।
आंशिक ओवरलैप वाली छवियों को निर्धारित करने के लिए, हमने एक विधि विकसित की, जिसका सार इस प्रकार था। दो छवियां एक दूसरे को ओवरलैप करती हैं, जिसमें 50 पिक्सेल की चौड़ाई होती है।
परिणामी विंडो में, प्रत्येक पिक्सेल के लिए, अंतर को RGB घटकों की गणना की जाती है, जिसके बाद पिक्सेल की सापेक्ष संख्या की गणना की जाती है, जिसके लिए R, G और B के मूल्यों में अंतर प्रत्येक घटक के लिए 20 से कम है - हम इन पिक्सेल को "काला" कहेंगे। यह संख्या दर्शाती है कि पिक्सल एक दूसरे पर सुपरइम्पोज़ किए गए रंग कितने करीब थे और इस तरह यह पहली और दूसरी छवि के सुपरिंपोज्ड हिस्से की निकटता की डिग्री निर्धारित करता है।
उसके बाद, विंडो को 6 पिक्सेल द्वारा स्थानांतरित किया जाता है और प्रक्रिया को दोहराया जाता है जब तक कि ओवरले विंडो की चौड़ाई 150 पिक्सल (आधी छवि) तक बढ़ जाती है। एक ही प्रक्रिया एक ही छवियों के लिए दोहराई जाती है जिसमें विपरीत पक्षों (पहले, दूसरे के बाईं ओर पहली छवि के दाईं ओर, और फिर, इसके विपरीत, पहले के बाईं ओर दूसरी छवि के दाईं ओर) को दोहराया जाता है।
उदाहरण के लिए, छवियों पर विचार करें:
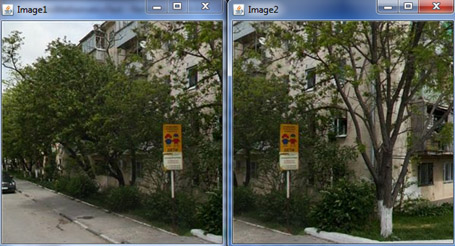
हम इन छवियों की पुनरावृत्ति ओवरले प्रक्रिया और ओवरले विंडो में पिक्सेल अंतर की गणना दिखाते हैं:
ओवरले की पुनरावृत्ति के आधार पर डार्क पिक्सलों की सापेक्ष संख्या में परिवर्तन का ग्राफ:
जैसा कि आप देख सकते हैं, 13 वें पुनरावृत्ति पर, हमें एक महत्वपूर्ण शिखर मिला, जिसका अर्थ है कि हम ओवरलैप को यथासंभव सटीक रूप से प्राप्त करते हैं, जो कि चित्रण द्वारा भी पुष्टि की जाती है।
इस प्रक्रिया के बाद, श्रृंखला में प्रत्येक जोड़ी की छवियों के लिए, हमारे पास "ब्लैक" पिक्सल के सापेक्ष संख्या के मूल्यों के साथ दो वैक्टर हैं और उनमें से अधिकतम की तलाश करें। यह उनके आंशिक ओवरलैप द्वारा दो छवियों की निकटता का मीट्रिक है। दूसरे शब्दों में, हम यह निर्धारित करते हैं कि ओवरलैपिंग करते समय दो छवियां कितनी मेल खाती हैं।
इस मीट्रिक की स्पष्ट समस्याएं शुरू में अंधेरे चित्र (रात पैनोरमा, आदि) हैं, क्योंकि एक अंधेरे क्षेत्र को एक अंधेरे क्षेत्र में लागू करने के बाद, आर, जी, बी के मूल्यों में अंतर छोटा होगा, इस तथ्य के बावजूद कि छवियां वास्तविक ओवरलैप नहीं हो सकती हैं। । इस समस्या को हल करने के लिए, प्रक्रिया शुरू करने से पहले, प्रत्येक छवि के लिए अंधेरे पिक्सेल की कुल संख्या की जांच की जाती है, और यदि यह काफी बड़ा है (छवि का 70% से अधिक), तो इस मीट्रिक का उपयोग करके ऐसी श्रृंखला का विश्लेषण नहीं किया जाता है। ऐसी श्रृंखला का एक उदाहरण:
इस तरह की मीट्रिक को लागू करते समय दूसरी समस्या छवि है, जिसका ओवरलैप सटीक नहीं है, लेकिन कुछ विकृतियां हैं:
-perspektivnye:
ओवरलैप में वस्तु (कार) की उपस्थिति:
ओवरलैप (पेड़ों, इमारतों पर जटिल बनावट, चकाचौंध) पर अत्यधिक विस्तृत वस्तुओं की उपस्थिति जो आदर्श रूप से एक-दूसरे को "ओवरलैप" नहीं कर सकती हैं और ऊपर वर्णित प्रक्रिया को लागू करते समय "ब्लैक" पिक्सल की एक उच्च सापेक्ष राशि देते हैं:
इसके अलावा, इस तथ्य के बावजूद कि समस्या के विवरण में आंशिक ओवरलैप का उल्लेख किया गया था, उसी पैनोरमा से तस्वीरों के लिए एक शर्त के रूप में, वहाँ काफी बड़ी संख्या में एपिसोड थे जहां तस्वीरों में ओवरलैप नहीं था:
इस मामले में, शोधन मेट्रिक्स का उपयोग किया गया था, जिसे बाद में वर्णित किया जाएगा।
ओवरले मीट्रिक से जुड़ी तीसरी समस्या मीट्रिक थ्रेसहोल्ड (दो पक्षों से ओवरले गुजरते समय "ब्लैक" पिक्सल की अधिकतम संख्या) का निर्धारण था, जब हम कह सकते हैं कि दो छवियों में आंशिक ओवरलैप है या नहीं।
इस समस्या का प्रारंभिक समाधान एक स्थिर सीमा का विकल्प था, जिसके मूल्य को प्रशिक्षण के नमूने में एक निश्चित चरण के साथ एक निश्चित सीमा में अनुभवजन्य चयन द्वारा चुना गया था। इस प्रकार, हमने स्थैतिक सीमा का एक निश्चित मूल्य प्राप्त किया, जिस पर प्रशिक्षण नमूने पर सार्वजनिक मूल्यांकन का परिणाम अधिकतम था। हालांकि, यह स्पष्ट है कि यह दृष्टिकोण पर्याप्त रूप से प्रभावी नहीं है, क्योंकि एक ही सीमा अलग-अलग तस्वीरों की श्रृंखला में अच्छी तरह से फिट नहीं होती है (उदाहरण के लिए, श्रृंखला ए में, दो तस्वीरों में एक अतिव्याप्त ओवरलैप है और मीट्रिक 95% का परिणाम देता है; अत्यधिक विस्तृत वस्तु है और मीट्रिक ने 70% का परिणाम दिया है, जो श्रृंखला ए से 95% की तुलना में काफी छोटा है, लेकिन श्रृंखला बी के भीतर अन्य तस्वीरों की तुलना में बहुत बड़ा हो सकता है)। इसके अलावा, प्रशिक्षण नमूना जिस पर हमने सीमा का चयन किया था वह छोटा था और पर्याप्त प्रतिनिधि नहीं था।
इन समस्याओं के संबंध में, यह निर्णय लिया गया कि ओवरले मीट्रिक द्वारा निकटता का निर्धारण करने के लिए सीमा को प्रत्येक श्रृंखला के लिए अलग से गणना की जानी चाहिए। सबसे पहले, मीट्रिक मूल्य को श्रृंखला में सभी तस्वीरों के लिए जोड़े में गणना की जाती है, जिसके बाद इन अनुमानों का औसत-वर्ग निर्धारित किया जाता है। मूल-माध्य-वर्ग मान को इस विचार से चुना गया था कि बहुत अधिक या बहुत कम मान अभिव्यंजक हैं और बताते हैं कि दो तस्वीरें एक ही चित्रमाला से संबंधित हैं या, इसके विपरीत, उनका अंतर बहुत बड़ा है, इसलिए इन चोटियों का आरोही द्वारा श्रृंखला के औसत स्कोर पर एक मजबूत प्रभाव होना चाहिए। वर्ग जब औसत स्कोर की गणना। उसके बाद, प्रत्येक रेटिंग की तुलना औसत रेटिंग के साथ की जाती है और अगर यह उससे कुछ बड़ा होता है (कुछ मार्जिन के साथ), तो फोटो को उसी पैनोरमा से संबंधित माना जाता है। यदि ऐसा कोई आरक्षित नहीं है, तो इसका मतलब है कि श्रृंखला के सभी चित्रों में लगभग समान मूल्य हैं, जिसका अर्थ यह हो सकता है कि इस श्रृंखला में कोई अतिरिक्त चित्र नहीं हैं, या यह कि मीट्रिक काम नहीं किया है और परिणाम को आगे स्पष्ट करना आवश्यक है।
प्रत्येक श्रृंखला के लिए गतिशील दहलीज निर्धारण दृष्टिकोण का उपयोग करते हुए, सार्वजनिक मूल्यांकन के परिणाम में दो दहाई से अधिक सुधार हुआ।
2. स्पेक्ट्रम सहसंबंध मीट्रिक
इस मीट्रिक का उपयोग श्रृंखला के लिए किया गया था जिसमें एक पैनोरमा से छवियों पर ओवरलैप स्पष्ट नहीं था और एक ओवररिक मीट्रिक का उपयोग करके खराब रूप से निर्धारित किया गया था। पर्याप्त रूप से बड़ी संख्या में एपिसोड श्रृंखला में, चित्रमाला और अतिरिक्त छवियों की तस्वीरें पूरी तरह से अलग-अलग परिस्थितियों (मौसम, दिन के समय, दृश्य संरचना (भवन और वन, उदाहरण के लिए), आदि) के तहत खींची गईं, जो रंगों के वितरण में उनके बीच एक महत्वपूर्ण अंतर देती हैं और छवियों में चमक।
इसलिए, रंगों के वितरण में समानता / अंतर का मूल्यांकन करने के लिए, हमने श्रृंखला से प्रत्येक चित्र को 10 मूल्यों के एक स्पेक्ट्रम (हिस्टोग्राम) में रखा: इंद्रधनुष के रंग (लाल, नारंगी, पीला, हरा, नीला, नीला, बैंगनी) और तटस्थ रंग: सफेद, ग्रे और काला। इंद्रधनुष के रंगों के लिए, ह्यू घटक के साथ HSV रंग स्थान का उपयोग किया गया था, जो 0-360 की सीमा में है और पिक्सेल के स्वर को दर्शाता है। हालांकि, इस दृष्टिकोण के साथ, रंग रेंज के तहत प्रत्येक में चमक घटक पर विचार किए बिना, हम सफेद, ग्रे और काले रंगों को शामिल करेंगे, जैसा कि आंकड़े में दिखाया गया है:
इसलिए, सफेद, ग्रे और काले रंग को बाहर करने के लिए, आरजीबी अंतरिक्ष में प्रत्येक पिक्सेल के घटकों को पहले इन रंगों की श्रेणियों से संबंधित के लिए जाँच की जाती है (सफेद के लिए, सभी घटक सीमा में होना चाहिए: 225-255, ग्रे के लिए: 125-225, काले के लिए - 0- 30)।
स्पेक्ट्रम के प्रत्येक घटक का अर्थ है छवि में एक या किसी अन्य उप-श्रेणी के रंगों की सापेक्ष संख्या, दूसरे शब्दों में, छवि में रंगों के वितरण को दर्शाता है। यह कुछ इस तरह दिखता है:
चूंकि प्रत्येक स्पेक्ट्रम 10 मानों का एक सदिश राशि है, पियरसन सहसंबंध गुणांक का उपयोग किसी श्रृंखला में छवियों की एक जोड़ी के स्पेक्ट्रा के बीच संबंध के अस्तित्व को निर्धारित करने के लिए किया गया था:
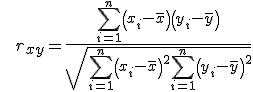
इस दृष्टिकोण ने खुद को बहुत अच्छी तरह से साबित कर दिया है, और सहसंबंध का मूल्य उन छवियों के लिए तेजी से बढ़ गया है जिनका रंग वितरण समान था।
इस मीट्रिक की एक महत्वपूर्ण समस्या यह है कि ओवरले मीट्रिक की तरह, थ्रेशोल्ड की परिभाषा जो दो छवियों के लिए सहसंबंध गुणांक के मूल्य को पार करना चाहिए ताकि यह कहा जा सके कि वे एक ही चित्रमाला से संबंधित हैं। इस समस्या को हल करने के लिए, हमने श्रृंखला में माध्य वर्ग सहसंबंध मान द्वारा प्रत्येक श्रृंखला के लिए सीमा के गतिशील निर्धारण के साथ एक विधि का उपयोग किया।
दूसरी समस्या यह है कि ऐसी श्रृंखलाएं हैं जिनमें एक पैनोरमा फोटो और एक शानदार एक के पास रंगों का एक बहुत करीब वितरण होता है (उदाहरण के लिए, आकाश और हरियाली का रंग), जो झूठी सकारात्मकता देता है।
तीसरी समस्या एक चित्रमाला से छवियां हैं, जिनमें से एक पर एक बड़ी वस्तु दिखाई देती है (उदाहरण के लिए, एक गुजरती हुई कार), जो कभी-कभी आधी छवि तक पहुंच जाती है। इस मामले में, ऐसी छवि के लिए वर्णक्रमीय वितरण नाटकीय रूप से बदल जाता है (बहुत नीला दिखाई देता है, उदाहरण के लिए, जो चित्रमाला में अन्य छवियों में नहीं था) और सहसंबंध अन्य वर्णमाला चित्रों के वर्णक्रम के साथ अपने स्पेक्ट्रम की निर्भरता नहीं दिखा सकता है।
3. सर्फ़ डिस्क्रिप्टिव मेट्रिक
SURF (स्पीड अप रोबस्ट फीचर्स) विधि छवियों को पहचानने और उनकी समानता का निर्धारण करने के लिए सबसे कुशल और सबसे तेज़ आधुनिक एल्गोरिदम में से एक है।
विधि का मुख्य बिंदु छवि पर कुछ प्रमुख बिंदुओं और उनके आसपास के छोटे क्षेत्रों को उजागर करना है। मुख्य बिंदु को एक ऐसा बिंदु माना जाता है जिसमें कुछ संकेत होते हैं जो इसे बिंदुओं के थोक से महत्वपूर्ण रूप से अलग करते हैं। उदाहरण के लिए, यह लाइनों के किनारों, छोटे हलकों, रोशनी में तेज बदलाव, कोण, आदि हो सकता है। अंकों के आसपास के छोटे क्षेत्रों का चयन किया जाता है क्योंकि छवि का एक छोटा क्षेत्र परिप्रेक्ष्य और बड़े पैमाने पर विकृतियों के लिए अतिसंवेदनशील है, लेकिन बहुत छोटे क्षेत्र भी उपयुक्त नहीं हैं, क्योंकि वे बहुत कम जानकारी रखते हैं।
SURF पद्धति हेसियन मैट्रिक्स का उपयोग करते हुए एकवचन बिंदुओं की खोज करती है, जो निर्धारक चमक ढाल में अधिकतम परिवर्तनों के बिंदुओं पर एक चरम सीमा तक पहुंचती है और स्पॉट, कोण और रेखाओं के किनारों का अच्छी तरह पता लगाती है। प्रमुख बिंदुओं के उदाहरण:
यह विधि पैमाने पर अपरिवर्तनीय है, छवि तल में घूमती है, शोर करती है, अन्य वस्तुओं के साथ ओवरलैप करती है, चमक और विपरीत में परिवर्तन करती है। यही है, यह उन श्रृंखलाओं के लिए आदर्श है जो पहले दो मैट्रिक्स के लिए समस्याग्रस्त थे।
दो छवियों की तुलना करते समय मीट्रिक मूल्य सामान्य कुंजी बिंदुओं की संख्या थी। हमने देखा कि दस से अधिक अंकों की संख्या के साथ, अधिकांश मामलों में दो छवियों में सामान्य वस्तुएं हैं, इसलिए इस मीट्रिक के लिए एक स्थिर सीमा का उपयोग किया गया था, जो व्यावहारिक रूप से गलत सकारात्मकता नहीं देता था।
इस मीट्रिक ने हमें उन तस्वीरों को निर्धारित करने की अनुमति दी जो 360 डिग्री पैनोरमा में स्केल की गई थीं, जहां देखने के कोण बहुत अधिक बदलते हैं और बड़े परिप्रेक्ष्य और ज्यामितीय विकृतियां होती हैं, लेकिन एक ही समय में ऑब्जेक्ट बने रहते हैं और प्रमुख बिंदु रहते हैं। उदाहरण के लिए, ऐसी श्रृंखला में:
इस पद्धति का मुख्य नुकसान उच्च कम्प्यूटेशनल भार है, और, परिणामस्वरूप, लंबे समय तक संचालन समय। हालांकि, हमने इसे एक स्पष्टकर्ता के रूप में इस्तेमाल किया और सबसे अधिक समस्याग्रस्त और विवादास्पद स्थितियों में गणना की, इसलिए यह गणना की संख्या को कम करने के लिए निकला।
विधि के कार्यान्वयन के रूप में, OpenSURF 2.0 पुस्तकालय का उपयोग किया गया था।
आप एक उल्लेखनीय लेख में SURF विधि के बारे में अधिक पढ़ सकते हैं,
निरंतर छवि विशेषताओं का पता लगाना: SURF विधि , जहाँ से हमने
विधि के चित्रण और विवरण को स्पष्ट रूप से उधार लिया है :)
निर्णय तर्क
एक निश्चित श्रृंखला के भीतर छवियों की तुलना करने और उनके फायदे और नुकसान का विश्लेषण करने के साथ-साथ एक प्रशिक्षण नमूने पर परीक्षणों की एक श्रृंखला का निर्माण करने के लिए विकसित मेट्रिक्स होने के बाद, हमने एक निर्णय लेने वाला सबसिस्टम बनाया जो इन मैट्रिक्स के आधार पर उत्तर तैयार करना चाहिए: फोटो इस श्रृंखला में बहुत ही शानदार हैं।
पहले, श्रृंखला के लिए संभावित विकल्पों पर विचार करें:
1) एक चित्रमाला में 3 तस्वीरों की एक श्रृंखला में और 2 तस्वीरें बहुत ही कम हैं;
क) एक चित्रमाला में अतिरिक्त तस्वीरें;
ख) विभिन्न पैनोरमा से अतिरिक्त तस्वीरें;
2) एक चित्रमाला में 4 तस्वीरों की एक श्रृंखला में और 1 तस्वीर शानदार है;
3) कोई ज़रूरत से ज़्यादा नहीं हैं;
तस्वीरों की एक श्रृंखला को ध्यान में रखते हुए, सिस्टम चित्रों के साथ दो सेट बनाता है: pl 1 और pl 2। प्रारंभ में, एल्गोरिथ्म इन सेटों पर चित्र वितरित करता है, जो आपस में ओवरले मीट्रिक द्वारा गतिशील सीमा से अधिक होते हैं। उसके बाद, इन सेटों पर छवियों को वितरित करने के लिए निम्नलिखित तार्किक विकल्प संभव हैं। हम इन विकल्पों के लिए क्रियाओं का वर्णन करते हैं:
1) (0) (0) - यह विकल्प संभव नहीं है, क्योंकि डायनेमिक थ्रेशोल्ड का उपयोग करते समय, हमेशा ऐसी छवियां होंगी जिनमें ओवरलैप मीट्रिक इस श्रृंखला के अंदर द्विघात माध्य से अधिक होता है (यदि ओवरले मीट्रिक में "मार्जिन" को पार नहीं किया जाता है, तो श्रृंखला को विभाजित किया जाएगा। वर्णक्रमीय सहसंबंध मीट्रिक का उपयोग करके सेट, जिसमें "मार्जिन" प्रदान नहीं किया गया है)
2) (2) (2) - इस विकल्प का अर्थ है कि एल्गोरिथ्म ने निर्धारित किया है कि दो चित्र एक पैनोरमा में हैं, दो अन्य में हैं, लेकिन पांचवें के बारे में कुछ भी नहीं कह सकते हैं। इस मामले में, निम्नलिखित विकल्प संभव हैं:
A) पांचवा बहुवचन 1 में जाएगा, और बहुवचन 2 बहुरंगी हो जाएगा;
बी) पांचवा बहुवचन 2 में जाएगा, और बहुवचन 1 अतिरेक बन जाएगा;
सी) पांचवें दोनों सेटों में जाएंगे, फिर कोई अतिश्योक्ति नहीं होगी;
ई) कोई भी मीट्रिक यह निर्धारित नहीं कर सकता है कि कौन सा सेट पांचवीं तस्वीर का है, इसलिए, इस चित्र के सहसंबंध गुणांक का सबसे बड़ा मूल्य पहले सेट, दूसरे सेट की तस्वीरों के साथ है, और साथ ही सेट 1 और सेट 2 से चित्रों के सहसंबंध गुणांक का विश्लेषण किया जाता है। संयोजन सबसे बड़ा गुणांक मान के अनुसार होता है। स्पेक्ट्रा के सहसंबंध:- बहुवचन 1 और बहुवचन 2 संयुक्त हैं और 5 वीं तस्वीर शानदार होगी;- पीएल 1 और 5 वीं तस्वीर संयुक्त हो जाएगी और पीएल 2 शानदार होगा;- बहुवचन 2 और 5 वीं तस्वीर एकजुट होगी और बहुवचन 1 अतिरेक होगा।सभी शोधन स्पेक्ट्रम सहसंबंध गुणांक और सुर विधि के मीट्रिक के अनुसार होते हैं3) (3) (2) - यह अनुभवजन्य रूप से देखा गया है कि अधिकांश मामलों में प्रशिक्षण के नमूने में यह विकल्प तुरंत सही है और स्पष्टीकरण की आवश्यकता नहीं है (pl। 2 - अनावश्यक)। मामले में जब ऐसा नहीं होता है, तो त्रुटि बहुत स्थूल नहीं होगी और परिणाम के समग्र मूल्यांकन को बहुत प्रभावित नहीं करेगी;4) (2) (3) - पिछले पैराग्राफ के समान (pl। 1 - सुपरफ्लस);5) (3) (0) - इस मामले में, निम्नलिखित विकल्प संभव हैं:ए) दोनों चित्र बेमानी हैं (विकल्प (3) (2));बी) पैनोरमा में दो चित्रों में से एक को शामिल किया गया है, और पांचवां सुपरफ्लुअस (विकल्प (4) (1)) है;सी) दोनों चित्र पैनोरमा में शामिल किए गए हैं, कोई भी अति सुंदर नहीं हैं (विकल्प (5) (0));सभी शोधन स्पेक्ट्रम सहसंबंध गुणांक और SURF विधि6) (4) (0) के अनुसार होते हैं - इस मामले में, निम्नलिखित विकल्प संभव हैं:क) पैनोरमा में 5 वें चित्र को शामिल नहीं किया गया है, अर्थात, 5 वीं तस्वीर बहुत बढ़िया है;बी) 5 वें चित्र को पैनोरमा में शामिल किया गया है, इसमें कोई अतिश्योक्ति नहीं है;सभी शोधन स्पेक्ट्रम सहसंबंध गुणांक और एसयूआरएफ पद्धति7) (5) (0) - विकल्प के बिना मीट्रिक के अनुसार होते हैं। उत्तर कोई अतिरिक्त नहीं है।परिणामों का मूल्यांकन
धीरे-धीरे सार्वजनिक मूल्यांकन के मूल्य में वृद्धि करते हुए, अधिक से अधिक जटिल दृष्टिकोणों को लागू करते हुए, समस्या को पुनरावृत्त रूप से हल किया गया था।उच्चतम परिणाम ऊपर वर्णित निर्णय द्वारा प्राप्त किया गया था और प्रारंभिक सार्वजनिक मूल्यांकन में 0.945 की राशि थी। अंतिम परिणाम बढ़कर 0.967 हो गया। अंतिम नमूने में विजेता का परिणाम 0.994 था।एक श्रृंखला के विश्लेषण का समय लगभग 20 सेकंड था।अंतिम नमूने में परिणाम में इतनी तेज वृद्धि का मुख्य कारण, हमारी राय में, यह है कि श्रृंखला के अंतिम सेट को अधिक सावधानीपूर्वक जांचा गया था और संकलक में व्यावहारिक रूप से कोई त्रुटि नहीं थी, जो अक्सर प्रारंभिक चरण की श्रृंखला में पाए जाते थे।चूंकि यह मीट्रिक बहुत स्पष्ट नहीं है और इसका अर्थ बहुत स्पष्ट नहीं है, वास्तविक मान्यता परिणाम वे आंकड़े हैं जो हमें प्रशिक्षण नमूने पर प्राप्त हुए हैं (इस तरह के आंकड़े केवल उस पर प्राप्त किए जा सकते हैं, क्योंकि इसके उत्तर ज्ञात थे):बिल्कुल सही उत्तर: 85, 3%; विभिन्न प्रकार की त्रुटियों के साथ गलत उत्तर: 14.7%।यह परिणाम काफी अधिक है। त्रुटियों में पाई जाने वाली श्रृंखला का विश्लेषण करते समय, हम अक्सर इस तथ्य पर आते हैं कि हम स्वयं सही उत्तर (या सही एक, हमारी राय में, यैंडेक्स के साथ मेल नहीं खाते) निर्धारित नहीं कर सकते थे।उदाहरण के लिए, श्रृंखला में:
1 और 4 अतिरेक हैं (हालांकि छवियों 2, 3 और 5 के बीच बहुत कम समानता है)।और इस श्रृंखला में:
केवल पहली तस्वीर को ही शानदार माना जाता है। हमारी राय में, चौथा फोटोग्राफ 2,3 और 5 के साथ एक चित्रमाला में प्रवेश कर सकता है, और वहां प्रवेश नहीं करता है और यह निर्धारित करता है कि यह अवास्तविक है।परिणामों का विश्लेषण करने के बाद, वर्णित निर्णय के मुख्य नुकसान, हम मैट्रिक्स की अपर्याप्त संख्या और निर्णय लेने की एक कठोर तार्किक संरचना पर विचार करते हैं। वास्तव में, प्रशिक्षण के नमूने का उपयोग केवल एक विशेष पद्धति का त्वरित मूल्यांकन प्राप्त करने और आंकड़े एकत्र करने के लिए किया गया था; सिस्टम में कोई मशीन सीखने की सुविधा नहीं दी गई थी। हालांकि, कई अग्रणी टीमों ने, जो प्रारंभिक चरण में पहले 5-की में जगह ले ली थीं, अंतिम नमूना (0.975 से 0.941 तक) में इस तथ्य के कारण काफी कम हो गया कि उनकी प्रणाली प्रारंभिक प्रारंभिक सेट पर बहुत अधिक मुकर गई थी।मुझे आशा है कि आप रुचि रखते थे और आप इस लेख के अंत में आ गए :)। अन्य समाधानों (विजेताओं के निर्णय सहित) का विवरण यहां पाया जा सकता है: यैंडेक्स क्लब ।