प्राइम फाइंडिंग प्राइम के बारे में एक बार

यह नोट प्राइम नंबर खोजने के लिए चलनी एल्गोरिदम पर चर्चा करता है। हम एराटोस्थनीज की शास्त्रीय छलनी पर एक नज़र डालेंगे , लोकप्रिय प्रोग्रामिंग भाषाओं में इसके कार्यान्वयन की विशेषताएं, समांतरिकरण और अनुकूलन, और फिर अधिक आधुनिक और तेज Atkin चलनी का वर्णन करेंगे । यदि Eratosthenes की छलनी के बारे में सामग्री प्राथमिक रूप से शुरुआती लोगों को रेक पर चलने से बचाने के लिए है, तो Atkin चलनी एल्गोरिथ्म पहले Habrahabr पर वर्णित नहीं किया गया था।

यह तस्वीर स्टैनफोर्ड विश्वविद्यालय के परिसर में स्थापित अमूर्त अभिव्यक्तिवादी मार्क डि सुवरो "द सिव ऑफ एरटोस्थनीज" की मूर्ति को दिखाती है।

परिचय

स्मरण करो कि एक संख्या को अभाज्य कहा जाता है यदि इसके दो भिन्न भाजक हैं: एक और स्वयं। अधिक संख्या में विभाजकों वाली संख्याओं को यौगिक कहा जाता है। इस प्रकार, यदि हम कारकों में संख्याओं को विघटित कर सकते हैं, तो हम सरलता के लिए संख्याओं की जांच भी कर सकते हैं। उदाहरण के लिए, कुछ इस तरह:

function isprime(n){ if(n==1) // 1 -    return false; //     2  sqrt(n) for(d=2; d*d<=n; d++){ //   ,   if(n%d==0) return false; } //    ,   return true; } 

(इसके बाद, जब तक कि अन्यथा निर्दिष्ट न हो, एक जावास्क्रिप्ट-जैसा छद्म कोड प्रदान किया जाता है)
इस तरह के टेस्ट का रनिंग टाइम जाहिर तौर पर O ( n a ) होता है, यानी यह बिट लेंथ n के संबंध में तेजी से बढ़ता है। इस परीक्षण को विभाजक जाँच कहा जाता है ।

अप्रत्याशित रूप से, अपने भाजक को खोजे बिना किसी संख्या की सादगी का परीक्षण करने के कई तरीके हैं। यदि बहुपद फैक्टराइजेशन एल्गोरिथ्म एक अप्राप्य सपना है (जिस पर RSA एन्क्रिप्शन की ताकत आधारित है), तो 2004 में विकसित AKS सादगी परीक्षण [ 1 ] बहुपद समय में पूरा होता है। विभिन्न प्रभावी सादगी परीक्षण [2] में पाए जा सकते हैं।

यदि अब हमें पर्याप्त रूप से व्यापक अंतराल पर सभी अपराधों को खोजने की आवश्यकता है, तो पहला आवेग संभवतः अंतराल से प्रत्येक संख्या को व्यक्तिगत रूप से जांचना होगा। सौभाग्य से, अगर हमारे पास पर्याप्त मेमोरी है, तो आप तेज (और सरल) चलनी एल्गोरिदम का उपयोग कर सकते हैं । इस लेख में हम उनमें से दो पर चर्चा करेंगे: एराटोस्थनीज की शास्त्रीय छलनी, जिसे प्राचीन यूनानियों द्वारा भी जाना जाता है, और एटकिन छलनी, इस परिवार का सबसे आधुनिक आधुनिक एल्गोरिदम है।

एराटोस्थनीज की छलनी

प्राचीन ग्रीक गणितज्ञ इरेटोस्थनीज ने सभी एल्गोरिदम को खोजने के लिए निम्नलिखित एल्गोरिदम का प्रस्ताव दिया था जो किसी दिए गए संख्या n से अधिक नहीं है । लंबाई n की एक सरणी S लें और इसे इकाइयों के साथ भरें ( इसे अपरिवर्तित चिह्नित करें )। अब हम क्रमिक रूप से S [ k ] के तत्वों को देखेंगे, जो k = 2. से शुरू होते हैं। यदि S [ k ] = 1 है, तो सभी बाद की कोशिकाओं में शून्य ( क्रॉस आउट या वेट आउट ) से भरें जिनकी संख्या k के गुणक हैं । नतीजतन, हमें एक सरणी मिलती है जिसमें सेल 1 होते हैं और केवल अगर सेल नंबर एक प्राइम है।

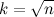
यदि आप नोटिस करते हैं कि आप बहुत समय बचा सकते हैं, क्योंकि n से कम एक समग्र संख्या के लिए, कम से कम एक भाजक से अधिक नहीं होना चाहिए , बुवाई की प्रक्रिया खत्म होने के लिए पर्याप्त है । यहाँ एराटोस्थनीज की छलनी का एक एनीमेशन है, जिसे विकिपीडिया से लिया गया है:



कुछ और संचालन को बचाया जा सकता है, यदि इसी कारण से, आप कश्मीर के गुणकों को पार करना शुरू करते हैं, तो 2k से नहीं , बल्कि संख्या k ^{2 से} ।



कार्यान्वयन निम्नलिखित रूप लेगा:

 function sieve(n){ S = []; S[1] = 0; // 1 -    //    for(k=2; k<=n; k++) S[k]=1; for(k=2; k*k<=n; k++){ //  k -  ( ) if(S[k]==1){ //    k for(l=k*k; l<=n; l+=k){ S[l]=0; } } } return S; } 

एराटोस्थनीज की छलनी की प्रभावशीलता आंतरिक चक्र की अत्यधिक सादगी के कारण होती है: इसमें सशर्त संक्रमण नहीं होता है, साथ ही विभाजन और गुणा जैसे "भारी" संचालन होते हैं।

हम एल्गोरिथ्म की जटिलता का अनुमान लगाते हैं। पहली स्ट्राइक के लिए N / 2 क्रियाओं की आवश्यकता होती है, दूसरी - n / 3, तीसरी - n / 5, आदि।

इसलिए ओ ( एन लॉग लॉग एन ) संचालन को एराटोस्थनीज की छलनी के लिए आवश्यक है। मेमोरी की खपत O ( n ) होगी।

अनुकूलन और समानांतरकरण

पहली छलनी अनुकूलन को इरेटोस्थनीज ने खुद प्रस्तावित किया था: चूंकि सभी सम संख्याओं में से केवल 2 सरल है, तो चलो आधी मेमोरी और समय बचाते हैं और हम बाहर लिखेंगे और केवल विषम संख्याओं को बोएंगे। एल्गोरिथम के इस तरह के संशोधन के कार्यान्वयन के लिए केवल कॉस्मेटिक परिवर्तनों ( कोड ) की आवश्यकता होगी।

अधिक उन्नत अनुकूलन (तथाकथित पहिया कारक ) इस तथ्य पर आधारित है कि 2, 3 और 5 को छोड़कर सभी सरल, आठ अंकगणितीय प्रगति में से एक में निहित हैं: 30 k +1, 30 k +7, 30 k +11; 30 k +13, 30 k +17, 30 k +19, 30 k 13:30 और 30 k +29। N तक के सभी प्राइम को खोजने के लिए, हम पहले से सभी प्राइमों की गणना करते हैं । अब हम आठ सिरों की रचना करेंगे, जिनमें से प्रत्येक में संबंधित अंकगणितीय प्रगति के तत्व शामिल होंगे, n से कम, और हम उनमें से प्रत्येक को एक अलग स्ट्रीम में बोएंगे। यही है, आप लाभ उठा सकते हैं: हमने न केवल मेमोरी खपत और सीपीयू लोड (मूल एल्गोरिथ्म की तुलना में चार गुना) को कम किया, बल्कि एल्गोरिदम के संचालन को भी समानांतर किया।

प्रगति कदम और sieves की संख्या में वृद्धि करके (उदाहरण के लिए, 210 के प्रगति कदम के साथ, हमें 48 s की आवश्यकता है, जो n के विकास के समानांतर में अन्य 4% संसाधनों को बचाएगा), यह लॉग लॉग n बार एल्गोरिथ्म की गति को बढ़ाने के लिए संभव है।

विभाजन

अगर हमारी तमाम चालों के बावजूद, रैम पर्याप्त नहीं है और एल्गोरिथम "स्वैप" बेशर्मी से क्या करना है? आप छोटे छलनी के अनुक्रम के साथ एक बड़ी छलनी को बदल सकते हैं और प्रत्येक को व्यक्तिगत रूप से बो सकते हैं। जैसा कि ऊपर, हमें सरल की एक सूची तैयार करनी होगी अतिरिक्त स्मृति O ( n ^½-½ ) लेता है। हमें स्ट्रेनर्स को बोने की प्रक्रिया में पाए जाने वाले साधारण को स्टोर करने की आवश्यकता नहीं है - हम उन्हें तुरंत आउटपुट स्ट्रीम में दे देंगे।

समान ओ ( n ^ε- elements) तत्वों की तुलना में, छोटे को बहुत छोटा करने की आवश्यकता नहीं है। तो आप मेमोरी खपत के स्पर्शोन्मुख व्यवहार में कुछ हासिल नहीं करेंगे, लेकिन ओवरहेड के कारण, आप प्रदर्शन में अधिक से अधिक खोना शुरू कर देंगे।

एराटोस्थनीज छलनी और एकल रेखा

हब्रहाब ने पहले अलग-अलग प्रोग्रामिंग भाषाओं में एक पंक्ति में इरेटोस्थनीज एल्गोरिदम का एक बड़ा चयन प्रकाशित किया था (एकल-पंक्ति संख्या 10)। दिलचस्प बात यह है कि ये सभी वास्तव में एराटोस्थनीज छलनी नहीं हैं और बहुत धीमी एल्गोरिदम को लागू करते हैं।

तथ्य यह है कि सेट को स्थिति से फ़िल्टर करना (उदाहरण के लिए,

 primes = primes.select { |x| x == prime || x % prime != 0 } 

(रूबी में) या उर्फ ​​लिस्ट कॉम्प्रिहेंशन जनरेटर लिस्ट (उदा।

 let pgen (p:xs) = p : pgen [x|x <- xs, x `mod` p > 0] 

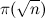
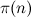
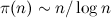
हास्केल पर) वे ठीक उसी प्रकार कहते हैं, जिसे चलनी एल्गोरिथ्म से बचने के लिए कहा जाता है, अर्थात्, विभाजन के तत्व-द्वारा-तत्व सत्यापन। नतीजतन, एल्गोरिथ्म की जटिलता कम से कम बढ़ जाती है (यह फ़िल्टरिंग की संख्या है) बार (फ़िल्टर्ड सेट के तत्वों की न्यूनतम संख्या), जहां - सरल की संख्या, n से अधिक नहीं, अर्थात, O ( n ^3/2-ε ) क्रियाओं तक।

सिंगल लाइन

 (n: Int) => (2 to n) |> (r => r.foldLeft(r.toSet)((ps, x) => if (ps(x)) ps -- (x * x to n by x) else ps)) 

स्कैला, इरेटोस्थनीज एल्गोरिथ्म के करीब है, जिसमें यह विभाजन की जांच से बचता है। हालांकि, सेट के अंतर के निर्माण की जटिलता उनमें से बड़े के आकार के आनुपातिक है, ताकि परिणाम एक ही ओ ( एन ^3/2-ε ) संचालन हो।

सामान्य तौर पर, इराटोस्थनीज की छलनी को प्रभावी रूप से अपरिवर्तनीय चर के कार्यात्मक प्रतिमान के ढांचे के भीतर लागू करना मुश्किल है। इस घटना में कि एक कार्यात्मक भाषा (उदाहरण के लिए, ओएसएएमएल) अनुमति देती है, यह नियमों का उल्लंघन करने और एक उत्परिवर्तित सरणी बनाने के लायक है। [ ३ ] में, यह चर्चा की गई कि कैसे आलसी लोगों की तकनीक का उपयोग करके हास्केल पर एराटोस्थनीज की छलनी को सही ढंग से लागू किया जाए।

Eratosthenes और PHP की चलनी

हम PHP में Eratosthenes एल्गोरिथ्म लिखते हैं। आपको निम्न जैसा कुछ मिलता है:

 define("LIMIT",1000000); define("SQRT_LIMIT",floor(sqrt(LIMIT))); $S = array_fill(2,LIMIT-1,true); for($i=2;$i<=SQRT_LIMIT;$i++){ if($S[$i]===true){ for($j=$i*$i; $j<=LIMIT; $j+=$i){ $S[$j]=false; } } } 

यहां दो समस्याएं हैं। इनमें से पहला डेटा प्रकार प्रणाली से संबंधित है और कई आधुनिक भाषाओं की विशेषता है। तथ्य यह है कि एराटोस्थनीज की छलनी उन परमाणु साइटों में सबसे प्रभावी रूप से लागू की जाती है जहां स्मृति में क्रमिक रूप से एक सजातीय सरणी की घोषणा करना संभव है। तब सेल S [i] के पते की गणना प्रोसेसर निर्देश के केवल एक जोड़े को ले जाएगी। PHP में एक सरणी वास्तव में एक विषम शब्दकोश है, अर्थात, यह मनमाने तार या संख्याओं द्वारा अनुक्रमित है और इसमें विभिन्न प्रकार के डेटा हो सकते हैं। इस स्थिति में, S [i] को ढूंढना अधिक समय लेने वाला कार्य हो जाता है।

दूसरी समस्या: PHP में सरणियाँ ओवरहेड पर भयानक हैं। मेरे 64-बिट सिस्टम पर, ऊपर के कोड से $ S का प्रत्येक तत्व 128 बाइट खाता है। जैसा कि ऊपर चर्चा की गई है, स्मृति में तुरंत पूरी छलनी को स्टोर करना आवश्यक नहीं है, आप इसे आंशिक रूप से संसाधित कर सकते हैं, लेकिन फिर भी, ऐसी लागतों को अस्वीकार्य के रूप में मान्यता दी जानी चाहिए।

इन समस्याओं को हल करने के लिए, यह अधिक उपयुक्त डेटा प्रकार चुनने के लिए पर्याप्त है - एक स्ट्रिंग!

 define("LIMIT",1000000); define("SQRT_LIMIT",floor(sqrt(LIMIT))); $S = str_repeat("\1", LIMIT+1); for($i=2;$i<=SQRT_LIMIT;$i++){ if($S[$i]==="\1"){ for($j=$i*$i; $j<=LIMIT; $j+=$i){ $S[$j]="\0"; } } } 

अब प्रत्येक तत्व ठीक 1 बाइट लेता है, और रनटाइम लगभग तीन गुना कम हो गया है। गति मापने की एक लिपि ।

एटकिन छलनी

1999 में, एटकिन और बर्नस्टीन ने समग्र संख्याओं की बुवाई का एक नया तरीका प्रस्तावित किया, जिसे एटकिन छलनी कहा जाता है। यह निम्नलिखित प्रमेय पर आधारित है।

प्रमेय। आज्ञा देना एक प्राकृतिक संख्या है जो किसी भी पूर्ण वर्ग द्वारा विभाज्य नहीं है। तो

1. यदि n को 4 k +1 के रूप में दर्शाया जा सकता है , तो यह सरल है अगर और केवल समीकरण 4 x ² + y ² = n के समीकरण के प्राकृतिक विलयनों की संख्या विषम है।
2. यदि n 6 k +1 के रूप में प्रतिनिधित्व करने योग्य है, तो यह सरल है अगर और केवल समीकरण 3 x ² + y ² = n समीकरण के प्राकृतिक समाधानों की संख्या विषम है।
3. यदि n को 12 k -1 के रूप में दर्शाया जा सकता है , तो यह सरल है अगर और केवल अगर समीकरण 3 x ² - y ² = n के प्राकृतिक समाधानों की संख्या, जिसके लिए x > y , विषम है।

प्रमाण [ 4 ] में पाया जा सकता है।

प्राथमिक संख्या सिद्धांत से यह निम्नानुसार है कि सभी सरल, बड़े 3, का फॉर्म 12 k +1 (केस 1), 12 k +5 (फिर 1), 12 k +7 (केस 2) या 12 k +11 (केस 3) है। ।

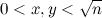
एल्गोरिथ्म को इनिशियलाइज़ करने के लिए, छलनी S को शून्य से भरें। अब प्रत्येक जोड़ी ( x , y ) के लिए, जहां , कोशिकाओं में मूल्यों को बढ़ाएँ S [4 x ² + y ² ], S [3 x ² + y ² ], और, अगर x > y , तो S [3 x ² - y ² ] में भी। गणनाओं के अंत में, फार्म 6 k odd 1 की कोशिकाओं की संख्या विषम संख्या वाले या तो primes हैं या उन्हें primes के वर्गों में विभाजित किया गया है।

अंतिम चरण के रूप में, हम क्रमिक रूप से सरल संख्याओं के माध्यम से जाएंगे और उनके वर्गों के गुणकों को पार करेंगे।

इस विवरण से देखा जा सकता है कि एटकॉस्टेनेस एल्गोरिथ्म में एन लॉग लॉग एन के बजाय एटकिन छलनी की जटिलता आनुपातिक है।

लेखक का सी में अनुकूलित कार्यान्वयन, प्राइमेन के रूप में प्रस्तुत किया गया है, एक सरलीकृत संस्करण विकिपीडिया पर है । हब्रहाब पर C # में Atkin चलनी प्रकाशित हुई थी ।

जैसा कि इरेटोस्थनीज छलनी में, पहिया कारक और विभाजन का उपयोग करते हुए, हम लॉग लॉग एन में असममित जटिलता को कम कर सकते हैं, और मेमोरी खपत - ओ ( एन ^{½ + ओ (1)} ) तक।

लघुगणक के लघुगणक के बारे में

वास्तव में, कारक लॉग एन बहुत बढ़ रहा है। धीरे-धीरे। उदाहरण के लिए, लॉग लॉग 10 ¹⁰⁰⁰⁰ Therefore 10. इसलिए, व्यावहारिक दृष्टिकोण से, इसे निरंतर माना जा सकता है, और एराटोस्थनीज एल्गोरिथ्म की जटिलता रैखिक है। यदि केवल साधारण लोगों की खोज आपके प्रोजेक्ट में महत्वपूर्ण कार्य नहीं है, तो आप एराटोस्थनीज की छलनी के मूल संस्करण का उपयोग कर सकते हैं (कुछ सम संख्याओं को बचाएं) और इस बारे में जटिल न हों। हालाँकि, बड़े अंतराल पर (2 ^{32 से} ) साधारण लोगों को खोजते समय, खेल मोमबत्ती के लायक होता है, Atkin के अनुकूलन और चलनी उत्पादकता बढ़ा सकते हैं।

पुनश्च ने सुंदरम छलनी के बारे में याद दिलाया। दुर्भाग्य से, यह केवल एक गणितीय जिज्ञासा है और हमेशा इरेटोस्थनीज और एटकिन की बहनों के लिए नीच है, या संपूर्ण विभाजक द्वारा जाँच करने के लिए।

साहित्य

[१] अग्रवाल एम।, कयाल एन।, सक्सेना एन। PRIMES पी में है। - एनाल्स ऑफ मैथ। 160 (2), 2004 ।-- पी। 781–793।
[२] क्रिप्टोग्राफी में वासिलेंको ओ.एन. संख्या-सिद्धांत संबंधी एल्गोरिदम। - एम।, आईसीएमएमओ, 2003 ।-- 328 पी।
[३] ओ'नील एमई इरावास्तीन की असली छलनी । - 2008।
[४] एटकिन एओएल, बर्नस्टीन डीजे प्राइम द्विआधारी द्विघात रूपों का उपयोग करके बैठता है । - गणित। अनि। 73 (246), 2003 ।-- पी। 1023-1030।