📺 🖖🏾 🚳 चेहरे की पहचान के लिए आधार के रूप में वायोला-जोन्स विधि 🧚🏾 💪 💅🏽

हालाँकि यह विधि 2001 में पॉल वियोला और माइकल जोन्स [1, 2] द्वारा विकसित और शुरू की गई थी, लेकिन वास्तविक समय की छवियों [2] में वस्तुओं की खोज के लिए मेरी पोस्ट लिखने के समय यह अभी भी मौलिक है। इस पद्धति के बारे में हैबरूस इंडालो विषय के निशान के बाद, मैंने खुद एक कार्यक्रम लिखने की कोशिश की, जो मेरे चेहरे पर भावना को पहचानता है, लेकिन, दुर्भाग्य से, मैंने उनके नाम निर्दिष्ट करने के अलावा, हेबर के कुछ एल्गोरिदम के संचालन के लापता सिद्धांत और विवरण को नहीं देखा। मैंने सब कुछ एक साथ एक जगह पर रखने का फैसला किया। मुझे तुरंत कहना होगा कि मैंने इन एल्गोरिदम का उपयोग करके सफलतापूर्वक अपना कार्यक्रम लिखा था। आपको उनके बारे में नीचे बात करने के लिए कैसे मिला, आप तय करते हैं, प्रिय हेब्रतचेटेली!

तो, इस बिंदु पर सही है।

वायोला जोन्स विधि विवरण

मूल सिद्धांत , जिस पर विधि आधारित है, इस प्रकार है:

चित्र अभिन्न प्रतिनिधित्व में उपयोग किए जाते हैं, जो आपको आवश्यक वस्तुओं की जल्दी से गणना करने की अनुमति देता है;
Haar के संकेतों का उपयोग किया जाता है , जिसकी मदद से वांछित वस्तु (इस संदर्भ में, चेहरे और इसकी विशेषताओं) की खोज होती है;
बूस्टिंग का उपयोग किया जाता है (अंग्रेजी से। बढ़ावा - सुधार, लाभ) छवि के दिए गए हिस्से में वांछित वस्तु के लिए सबसे उपयुक्त सुविधाओं का चयन करने के लिए;
सभी संकेत क्लासिफायरियर के इनपुट पर जाते हैं, जो परिणाम "सही" या "गलत" देता है;
सुविधाओं के कैस्केड का उपयोग उन खिड़कियों को जल्दी से करने के लिए किया जाता है जहां एक चेहरा नहीं पाया जाता है।

क्लासिफायर का प्रशिक्षण बहुत धीमा है, लेकिन चेहरे की खोज के परिणाम बहुत तेज हैं , यही वजह है कि छवि में चेहरे की पहचान का यह तरीका चुना गया था। वियोला जोन्स मान्यता दक्षता / गति के अनुपात के मामले में सर्वश्रेष्ठ में से एक है। इसके अलावा, इस डिटेक्टर में चेहरे की झूठी पहचान की बेहद कम संभावना है। एल्गोरिथ्म भी अच्छी तरह से काम करता है और लगभग 30 डिग्री तक एक मामूली कोण पर चेहरे की विशेषताओं को पहचानता है। 30 डिग्री से अधिक के झुकाव कोण के साथ, हिरासत का प्रतिशत तेजी से गिरता है। और यह मानक कार्यान्वयन में किसी व्यक्ति के मनमाने कोण पर एक ऐसे चेहरे का पता लगाने की अनुमति नहीं देता है, जो आधुनिक उत्पादन प्रणालियों में एल्गोरिथ्म का उपयोग करने में बहुत जटिल हो जाता है या असंभव हो जाता है, उनकी बढ़ती जरूरतों को ध्यान में रखता है।
उन सिद्धांतों का एक विस्तृत विश्लेषण जिस पर वायोला-जोन्स एल्गोरिथ्म आधारित है, की आवश्यकता है। सामान्य तौर पर यह तरीका स्कैनिंग विंडो के सामान्य सिद्धांत के अनुसार चेहरे और चेहरे की विशेषताओं के लिए दिखता है।

स्कैनिंग विंडो सिद्धांत

सामान्य तौर पर, डिजिटल छवि में किसी व्यक्ति के चेहरे और चेहरे की विशेषताओं का पता लगाने का कार्य इस तरह दिखता है:

एक छवि है जिस पर वांछित वस्तुएं हैं । यह आकार w * h के दो-आयामी मैट्रिक्स द्वारा दर्शाया गया है, जिसमें प्रत्येक पिक्सेल का एक मूल्य है:
- 0 255 अगर यह एक काली और सफेद छवि है;
- 0 255 ³ यदि यह एक रंग छवि है (घटक आर, जी, बी)।
अपने काम के परिणामस्वरूप, एल्गोरिथ्म को चेहरे और उनकी विशेषताओं को निर्धारित करना चाहिए और उन्हें चिह्नित करना चाहिए - खोज को आयताकार संकेतों के साथ छवि के सक्रिय क्षेत्र में किया जाता है, जिसकी सहायता से पाया गया चेहरा और इसकी विशेषताएं वर्णित हैं:
rectangle _i = {x,y,w,h,a}, (1.1)
जहाँ x, y, i-वें आयत के केंद्र के निर्देशांक हैं, w चौड़ाई है, h ऊँचाई है, आयत का झुकाव छवि के ऊर्ध्वाधर अक्ष में कोण है।

दूसरे शब्दों में, ड्राइंग और तस्वीरों के संबंध में, स्कैनिंग विंडो पर आधारित दृष्टिकोण का उपयोग किया जाता है : छवि को खोज विंडो (तथाकथित स्कैनिंग विंडो) द्वारा स्कैन किया जाता है, और फिर प्रत्येक स्थिति में क्लासिफायर लागू किया जाता है। प्रशिक्षण प्रणाली और सबसे महत्वपूर्ण विशेषताओं का चयन पूरी तरह से स्वचालित है और इसमें मानव हस्तक्षेप की आवश्यकता नहीं है, इसलिए यह दृष्टिकोण जल्दी से काम करता है।
इस सिद्धांत का उपयोग करके एक छवि में चेहरे खोजने और खोजने का कार्य अक्सर विशेषता विशेषताओं को पहचानने के तरीके पर अगला कदम होता है, उदाहरण के लिए, किसी व्यक्ति को किसी मान्यता प्राप्त चेहरे से सत्यापित करना या चेहरे के भावों को पहचानना।

एकीकृत छवि प्रतिनिधित्व

डेटा के साथ किसी भी क्रिया को करने के लिए, छवियों [3] का अभिन्न प्रतिनिधित्व वियोला-जोन्स विधि में किया जाता है। इस प्रतिनिधित्व को अक्सर अन्य तरीकों में उपयोग किया जाता है, उदाहरण के लिए, तरंग परिवर्तन, एसयूआरएफ और कई अन्य पार्स एल्गोरिदम में। एकीकृत प्रतिनिधित्व आपको किसी दिए गए चित्र में एक मनमानी आयत की कुल चमक की जल्दी से गणना करने की अनुमति देता है, और कोई भी आयत नहीं है, गणना समय स्थिर है।
एक छवि का अभिन्न प्रतिनिधित्व एक मैट्रिक्स है जो मूल छवि के समान आकार है । इसका प्रत्येक तत्व इस तत्व के बाईं ओर और ऊपर सभी पिक्सेल की तीव्रता का योग करता है । मैट्रिक्स तत्वों की गणना निम्न सूत्र का उपयोग करके की जाती है:

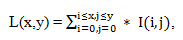(1.2)
जहाँ मैं (i, j) मूल छवि के पिक्सेल की चमक है।
मैट्रिक्स एल [x, y] का प्रत्येक तत्व आयत में पिक्सल का योग (0,0) से (x, y), अर्थात। प्रत्येक पिक्सेल का मूल्य (x, y) दिए गए पिक्सेल (x, y) के ऊपर और ऊपर सभी पिक्सेल के मूल्यों के योग के बराबर है। मैट्रिक्स की गणना रैखिक समय लेती है, छवि में पिक्सेल की संख्या के अनुपात में, इसलिए एकीकृत छवि की गणना एक पास में की जाती है।
मैट्रिक्स की गणना 1.3 सूत्र द्वारा संभव है:
L(x,y) = I(x,y) – L(x-1,y-1) + L(x,y-1) + L(x-1,y) (1.3)
इस तरह के अभिन्न मैट्रिक्स का उपयोग करके, आप बहुत जल्दी एक मनमाना आयत के पिक्सल की राशि की गणना कर सकते हैं, एक मनमाना क्षेत्र।
आयत ABCD में ऑब्जेक्ट D को हमारे लिए रूचि होने दें:

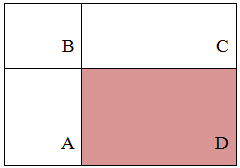
आकृति से यह स्पष्ट है कि आयत के अंदर का योग निम्नलिखित सूत्र के अनुसार समकोण और समीप आयतों के अंतर के रूप में व्यक्त किया जा सकता है:
S(ABCD) = L(A) + L() — L(B) — L(D) (1.4)
नीचे दिए गए चित्र में एक अनुमानित मिसकॉल दिखाया गया है:

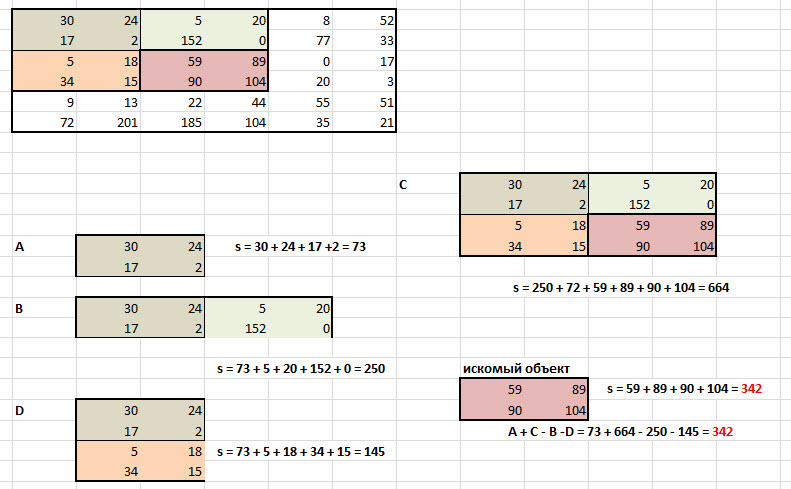
हर की निशानी

संकेत मानचित्रण f: X => D _{f है} , जहाँ D _f चिन्ह के स्वीकार्य मानों का समुच्चय है। यदि संकेत f ₁ , ..., f _{n दिए गए हैं} , तो संकेत x = (f ₁ (x), ..., f _n (x)) के वेक्टर को ऑब्जेक्ट x ∈ X का चारित्रिक वर्णन कहा जाता है। वस्तुओं के साथ वर्णनात्मक वर्णनात्मक पहचान करना संभव है। इसके अलावा, सेट X = D _f1 * ... * D _fn को फीचर स्पेस [1] कहा जाता है।
संकेत डी सेट के आधार पर निम्न प्रकारों में विभाजित हैं:

बाइनरी साइन, डी _एफ = {0,1};
नाममात्र विशेषता: डी _एफ - परिमित सेट;
क्रमिक विशेषता: डी _एफ - परिमित आदेश सेट;
मात्रात्मक विशेषता: डी _एफ - वास्तविक संख्याओं का समूह।

स्वाभाविक रूप से, विभिन्न प्रकार के संकेतों के साथ लागू समस्याएं हैं, सभी विधियां उन्हें हल करने के लिए उपयुक्त नहीं हैं।
मानक वियोला-जोन्स विधि में, नीचे की आकृति में दिखाए गए आयताकार विशेषताओं का उपयोग किया जाता है, उन्हें हरर प्राइमेटरी कहा जाता है:

OpenCV लाइब्रेरी में प्रयुक्त उन्नत वायोला-जोन्स विधि में, अतिरिक्त सुविधाओं का उपयोग किया जाता है:

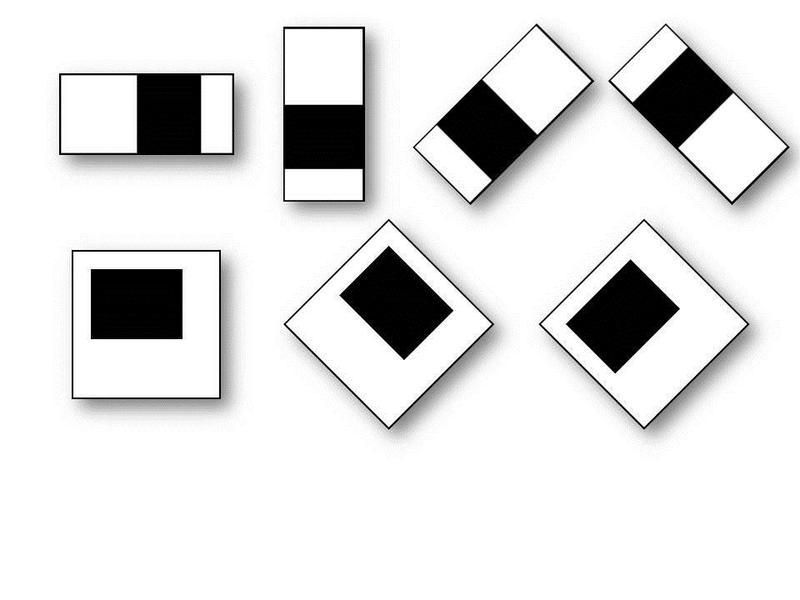
ऐसी सुविधा का परिकलित मान होगा
F = XY , (1.5)
जहाँ X चिन्ह के प्रकाश भाग द्वारा बंद किए गए बिंदुओं के चमक मानों का योग है, और Y चिन्ह के अंधेरे भाग द्वारा बंद किए गए बिंदुओं के चमक मूल्यों का योग है। उनकी गणना करने के लिए, हम ऊपर चर्चा की गई एक एकीकृत छवि की अवधारणा का उपयोग करते हैं।
Haar के संकेत क्रमशः X और Y अक्ष के साथ चमक ड्रॉप का एक मान देते हैं ।

विंडो स्कैन

कार्यक्रम में स्कैनिंग विंडो का दृश्य:

संकेत के साथ एक खिड़की को स्कैन करने के लिए एल्गोरिथ्म इस तरह दिखता है:

एक जांच की गई छवि है, एक स्कैन विंडो चयनित है, उपयोग की गई सुविधाओं का चयन किया जाता है;
इसके अलावा, स्कैनिंग विंडो छवि में क्रमिक रूप से 1 विंडो सेल के वेतन वृद्धि में ले जाना शुरू करती है (उदाहरण के लिए, विंडो का आकार 24 * 24 सेल है);
प्रत्येक विंडो में एक छवि को स्कैन करते समय, संकेतों के स्थान के लिए लगभग 200,000 विकल्पों की गणना स्कैनिंग विंडो में संकेतों के पैमाने और उनकी स्थिति को बदलकर की जाती है;
स्कैनिंग विभिन्न तराजू के लिए क्रमिक रूप से किया जाता है;
छवि को स्वयं नहीं बढ़ाया गया है, लेकिन स्कैनिंग विंडो (सेल का आकार बदलता है);
सभी पाए गए संकेत क्लासिफायर में आते हैं, जो "एक फैसले का प्रतिपादन करता है"।

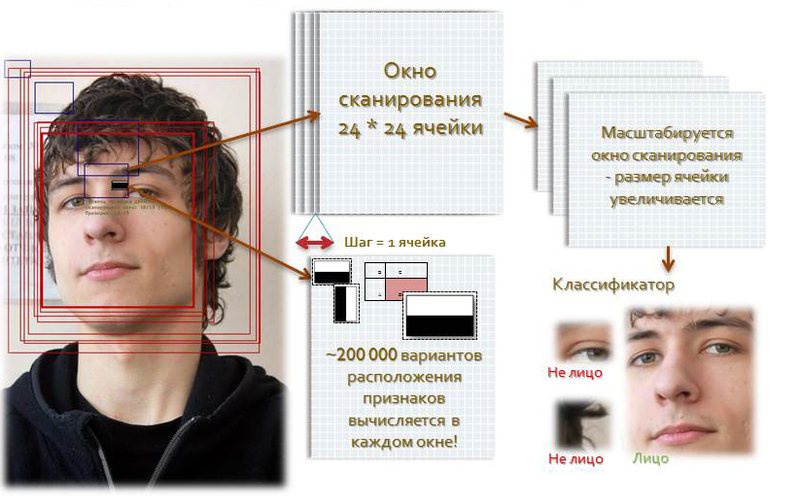
कम-शक्ति डेस्कटॉप पीसी पर सभी संकेतों की गणना करने के लिए खोज प्रक्रिया में बस अवास्तविक है। नतीजतन, क्लासिफायर केवल सभी विशेषताओं के एक विशिष्ट, आवश्यक सबसेट का जवाब देना चाहिए। यह पूरी तरह से तर्कसंगत है कि किसी विशिष्ट उपसमूह द्वारा व्यक्तियों को खोजने में क्लासिफायर के प्रशिक्षण की आवश्यकता है। यह कंप्यूटर को स्वचालित रूप से प्रशिक्षित करके किया जा सकता है।

एल्गोरिथ्म में प्रयुक्त मशीन लर्निंग मॉडल

मशीन प्रशिक्षण एक मॉड्यूल द्वारा नए ज्ञान प्राप्त करने की प्रक्रिया है। इस प्रक्रिया के लिए एक मान्यता प्राप्त परिभाषा है:

"मशीन लर्निंग एक विज्ञान है जो कंप्यूटर एल्गोरिदम का अध्ययन करता है जो आपके काम करते समय स्वचालित रूप से सुधार करता है।" (मिशेल, 1996)

। नीचे मशीन सीखने की प्रक्रिया है:

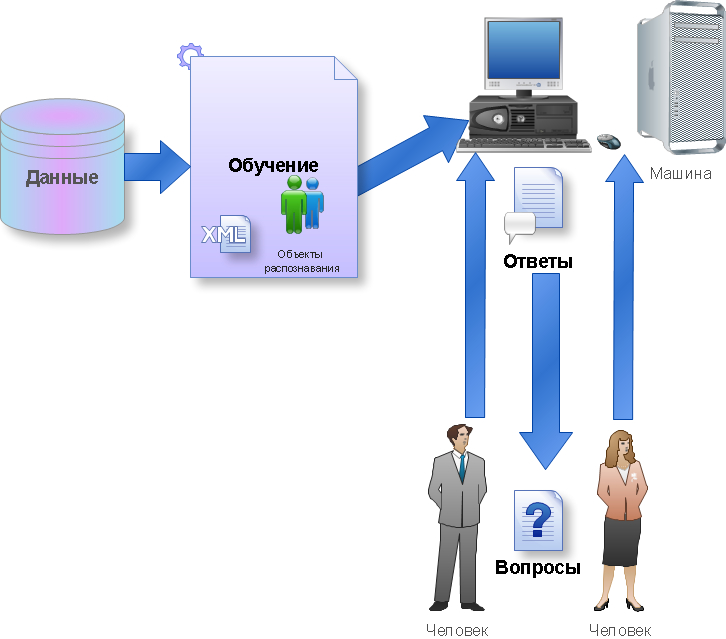
यह प्रक्रिया एक अवधारणा और प्रौद्योगिकी का हिस्सा है जिसे डेटा माइनिंग ( डेटा माइनिंग और डेटा माइनिंग) कहा जाता है, जिसमें मशीन लर्निंग के अलावा, डेटाबेस थ्योरी, आर्टिफिशियल इंटेलिजेंस, एल्गोरिथम, पैटर्न रिकग्निशन और अन्य जैसे विषय शामिल हैं।
वियोला-जोन्स पद्धति में मशीन सीखने से वर्गीकरण जैसी समस्या का समाधान होता है ।

वियोला-जोन्स विधि में क्लासिफायर ट्रेनिंग

एल्गोरिथ्म के संदर्भ में, कई ऑब्जेक्ट्स (चित्र) किसी तरह से कक्षाओं में विभाजित हैं। छवियों का एक सीमित सेट दिया गया है, जिसके लिए यह ज्ञात है कि वे किस वर्ग से संबंधित हैं (उदाहरण के लिए, यह वर्ग "नाक की ललाट स्थिति" हो सकती है)। इस सेट को ट्रेनिंग सेट कहा जाता है। शेष वस्तुओं की वर्गीय संबद्धता ज्ञात नहीं है। प्रारंभिक सेट [4] से एक मनमानी वस्तु को वर्गीकृत करने में सक्षम एल्गोरिथ्म का निर्माण करना आवश्यक है।
किसी वस्तु को वर्गीकृत करने का अर्थ उस संख्या (या वर्ग नाम) को इंगित करना है जिससे यह वस्तु संबंधित है।
किसी वस्तु का वर्गीकरण - इस विशिष्ट वस्तु के लिए इसके अनुप्रयोग के परिणामस्वरूप वर्गीकरण एल्गोरिथम द्वारा जारी वर्ग संख्या या नाम।
क्लासिफायर - वर्गीकरण समस्याओं में, यह एक अनुमानित कार्य है जो यह निर्णय करता है कि यह ऑब्जेक्ट किस वर्ग का है।
एक प्रशिक्षण सेट डेटा की एक सीमित संख्या है।
मशीन लर्निंग में, वर्गीकरण कार्य शिक्षक के साथ सीखने के खंड को संदर्भित करता है जब कक्षाएं विभाजित होती हैं । पैटर्न मान्यता अनिवार्य रूप से छवियों और संकेतों का एक वर्गीकरण है। पहचान और चेहरे की पहचान के लिए वायोला-जोन्स एल्गोरिथ्म के मामले में, वर्गीकरण दो-वर्ग है ।
वर्गीकरण इस प्रकार है:
एक्स - वह सेट है जिसमें वस्तुओं का विवरण संग्रहीत किया जाता है, वाई - वर्गों से संबंधित संख्याओं का परिमित सेट। उनके बीच एक संबंध है - मैपिंग Y *: X => Y. प्रशिक्षण नमूना का प्रतिनिधित्व X _m = {(x ₁ ,y ₁ ), …, (x _m ,y _m )} । फ़ंक्शन वेक्टर का निर्माण फीचर वेक्टर X से किया गया है, जो X के किसी भी संभावित अवलोकन के लिए एक उत्तर देता है और ऑब्जेक्ट x .X को वर्गीकृत करने में सक्षम है। यह सरल नियम नए डेटा पर अच्छी तरह से काम करना चाहिए।

AdaBoost बूस्टिंग और विकास एल्गोरिथ्म में इस्तेमाल किया

इस तरह के एक जटिल प्रशिक्षण की समस्या को हल करने के लिए, एक बढ़ावा देने वाली तकनीक है।
बूस्टिंग एक ऐसा तरीका है जो विश्लेषणात्मक मॉडलों की सटीकता को बढ़ाने में योगदान देता है। एक प्रभावी मॉडल जो कुछ वर्गीकरण त्रुटियों की अनुमति देता है उसे "मजबूत" कहा जाता है। "कमजोर" , इसके विपरीत, मज़बूती से कक्षाओं को अलग करने या सटीक भविष्यवाणियां करने की अनुमति नहीं देता है, काम में बड़ी संख्या में त्रुटियां करता है। इसलिए, अंग्रेजी से (बूस्टिंग - बूस्टिंग - बढ़ते, मजबूत, सुधार) को बढ़ावा देने का शाब्दिक अर्थ है "कमजोर" मॉडल का "मजबूत करना" [5] मशीन सीखने के एल्गोरिदम की क्रमिक रूप से निर्माण के लिए एक प्रक्रिया है, जब प्रत्येक बाद का एल्गोरिथ्म सभी पिछले एल्गोरिदम की रचना की कमियों की भरपाई करना चाहता है।
90 के दशक के उत्तरार्ध में रॉबर्ट शेपायर द्वारा बढ़ावा देने के विचार को प्रस्तावित किया गया था [6], जब एक अच्छा पाने के लिए बहुत सारे बुरे (यादृच्छिक से अलग) लर्निंग एल्गोरिदम की समस्या का हल खोजना आवश्यक था। इस तरह के एक विचार का आधार सहपाठियों की एक श्रृंखला (पहनावा) [5, 6] का निर्माण है, जिसे कैस्केड कहा जाता है, जिनमें से प्रत्येक (पहले को छोड़कर) पिछले एक की गलतियों से सीखता है । उदाहरण के लिए, पहले बूस्टिंग एल्गोरिदम में से एक Boost1 ने 3 मॉडलों का एक कैस्केड का उपयोग किया, जिनमें से पहला संपूर्ण डेटा सेट पर प्रशिक्षित किया गया, दूसरा उदाहरणों के नमूने पर, जिसमें से आधे ने सही उत्तर दिए, और तीसरा उदाहरण "उत्तर" पर दिया। पहले दो भाग। इस प्रकार, क्लासिफ़ायर के एक कैस्केड द्वारा उदाहरणों का अनुक्रमिक प्रसंस्करण होता है, और इसलिए कि प्रत्येक बाद के लिए कार्य अधिक कठिन हो जाता है। परिणाम सरल मतदान द्वारा निर्धारित किया जाता है: उदाहरण उस वर्ग को संदर्भित करता है जो कैस्केड के अधिकांश मॉडलों द्वारा जारी किया जाता है।
बूस्टिंग एक लालची एल्गोरिथ्म है - एक लालची एल्गोरिथ्म - एक एल्गोरिथ्म जो हर कदम पर स्थानीय रूप से इस उम्मीद में सबसे अच्छा विकल्प बनाता है कि अंतिम समाधान इष्टतम होगा। वर्गीकरण गुणवत्ता के संदर्भ में निर्णय पेड़ों पर बूस्टिंग को सबसे प्रभावी तरीकों में से एक माना जाता है। कई प्रयोगों में, संरचना बढ़ने के साथ एक स्वतंत्र परीक्षण नमूने पर त्रुटि दर में लगभग असीमित कमी देखी गई थी। इसके अलावा, पूरे प्रशिक्षण नमूने की त्रुटि-मुक्त मान्यता प्राप्त करने के बाद भी परीक्षण नमूने की गुणवत्ता में अक्सर सुधार होता रहा। इसने लंबे समय से आयोजित विश्वास को पलट दिया है कि सामान्यीकरण क्षमता को बढ़ाने के लिए एल्गोरिदम की जटिलता को सीमित करना आवश्यक है। बढ़ावा देने के उदाहरण का उपयोग करते हुए, यह स्पष्ट हो गया कि मनमाने ढंग से जटिल रचनाओं की गुणवत्ता अच्छी हो सकती है यदि वे ठीक से ट्यून किए गए हों [5]।
गणितीय रूप से, बूस्टिंग इस प्रकार है:
सेट X और Y के साथ, एक सहायक सेट R, जिसे अनुमान स्थान कहा जाता है , पेश किया गया है। हम एल्गोरिदम को एक सुपरपोज़िशन (x) = C (b (x)) का रूप मानते हैं, जहाँ फ़ंक्शन b: X → R को एल्गोरिथम ऑपरेटर कहा जाता है, और फ़ंक्शन C: R → Y निर्णय नियम है ।
कई वर्गीकरण एल्गोरिदम में बस ऐसी संरचना होती है: पहले, कक्षाओं के लिए किसी ऑब्जेक्ट के अनुमान की गणना की जाती है, फिर एक निर्णय नियम इन अनुमानों को एक वर्ग संख्या में अनुवाद करता है। मूल्यांकन के मूल्य, एक नियम के रूप में, वर्गीकरण के आत्मविश्वास की डिग्री की विशेषता है।
एल्गोरिथम रचना - a: X → Y एल्गोरिथ्म का रूप
a(x) = C(F(b ₁ (x), . . . , b _T (x)), x ∈ X (1.6)
एल्गोरिथम ऑपरेटरों से बना b _t : X → R, t = 1, ..., T, सही संचालन F: R ^T → R और निर्णय नियम C: R → Y.
बुनियादी एल्गोरिदम कार्यों को एक _टी (एक्स) = सी (बी _टी (एक्स)), और एक निश्चित निर्णय नियम सी के लिए, ऑपरेटरों बी _टी (एक्स) को निरूपित करते हैं।
फॉर्म एफ (बी ₁ , ..., बी _टी ) के सुपरस्पेशिएशन एक्स से आर तक मैपिंग हैं, जो कि, फिर से, एल्गोरिथम ऑपरेटर हैं।
दो असमान वर्गों में वर्गीकृत करने की समस्याओं में, वास्तविक संख्याओं का एक सेट आमतौर पर अनुमानों के स्थान के रूप में उपयोग किया जाता है। निर्णायक नियमों में विन्यास योग्य पैरामीटर हो सकते हैं। तो, वियोला-जोन्स एल्गोरिथ्म में, एक थ्रेशोल्ड निर्णय नियम का उपयोग किया जाता है , जहां, एक नियम के रूप में, ऑपरेटर को पहले शून्य मान पर बनाया जाता है, और फिर इष्टतम मूल्य का चयन किया जाता है। बुनियादी एल्गोरिदम के अनुक्रमिक प्रशिक्षण की प्रक्रिया का उपयोग, शायद, सबसे अधिक बार रचनाओं के निर्माण में किया जाता है।
कार्य की बारीकियों के आधार पर, शटडाउन मानदंड का उपयोग अलग-अलग किया जा सकता है; कई मानदंडों का एक साथ भी उपयोग किया जा सकता है:

बुनियादी एल्गोरिदम टी की एक पूर्व निर्धारित संख्या का निर्माण किया जाता है;
प्रशिक्षण सेट पर सटीकता प्राप्त की जाती है;
नियंत्रण नमूने में प्राप्त सटीकता को पिछले कुछ चरणों में एक निश्चित एल्गोरिदम पैरामीटर के साथ सुधार नहीं किया जा सकता है।

इस दृष्टिकोण का विकास एडॉबस्ट बूस्टिंग एल्गोरिदम ( एडाप्टिव बूस्टिंग ) के एक अधिक उन्नत परिवार का विकास था, जो 1999 में जोआब फ्रंड और रॉबर्ट शेपायर द्वारा प्रस्तावित था [9], जो मनमाने ढंग से कक्षावार संख्या का उपयोग कर सकता है और एक सेट पर प्रशिक्षण प्रदान कर सकता है। उदाहरण, उन्हें अलग-अलग चरणों में वैकल्पिक रूप से लागू करना।
हम वर्गीकरण समस्या को दो वर्गों में मानते हैं, Y = {,1, + 1}। उदाहरण के लिए, बुनियादी एल्गोरिदम भी केवल दो उत्तर and1 और +1 लौटाते हैं, और निर्णय नियम तय होता है: C (b) = चिन्ह (b)। वांछित एल्गोरिथम रचना का रूप है:

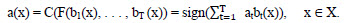(1.7)
संरचना Q _t की गुणवत्ता के कार्य को प्रशिक्षण सेट में इसके द्वारा की गई त्रुटियों की संख्या के रूप में परिभाषित किया गया है:

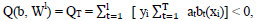(1.8)
जहाँ W ^l = (w ₁ , ..., w _l ) वस्तुओं के भार का सदिश है।
AdaBoosting समस्या को हल करने के लिए, थ्रेशोल्ड लॉस फंक्शन [z <0] की एक घातीय सन्निकटन की जरूरत है, जिसमें एक्सपोर्टर E ^z = e ^-z (नीचे दिए गए AdaBoost के कार्य को दर्शाने वाली आकृति में देखा गया है)।
तो, सामान्य अनुकूली लाभ एल्गोरिथ्म, AdaBoost, इस प्रकार है:

:
Y = {−1,+1}, b ₁ (x), . . . , b _T (x) −1 + 1, X ^l – .

: Y = {−1,+1}, b ₁ (x), . . . , b _T (x) −1 + 1, X ^l – .
: Y = {−1,+1}, b ₁ (x), . . . , b _T (x) −1 + 1, X ^l – .
: Y = {−1,+1}, b ₁ (x), . . . , b _T (x) −1 + 1, X ^l – .

:
Y = {−1,+1}, b ₁ (x), . . . , b _T (x) −1 + 1, X ^l – .

:
1. :
w _i := 1/ℓ, i = 1, . . . , ℓ; (1.9)
t = 1, . . . , T, :
2 .  (1.10)
2 .  (1.11)
3. . .  , b _t , , b _t x _i . , , :
 (1.12)
4. :
 (1.13)

तैयारी के चरणों में AdaBoost का कार्यान्वयन, दूसरा चरण, 12 वीं और 642 वीं आकृति में दिखाया गया है। एक निश्चित संख्या में बुनियादी एल्गोरिदम (कहते हैं, दसियों के एक जोड़े) के निर्माण के बाद, आपको वस्तुओं के भार के वितरण का विश्लेषण करने की आवश्यकता है। सबसे बड़े वजन वाले ऑब्जेक्ट्स w _मैं संभवतः शोर उत्सर्जन है जिसे नमूना से बाहर रखा जाना चाहिए, और फिर फिर से रचना का निर्माण शुरू करना चाहिए।

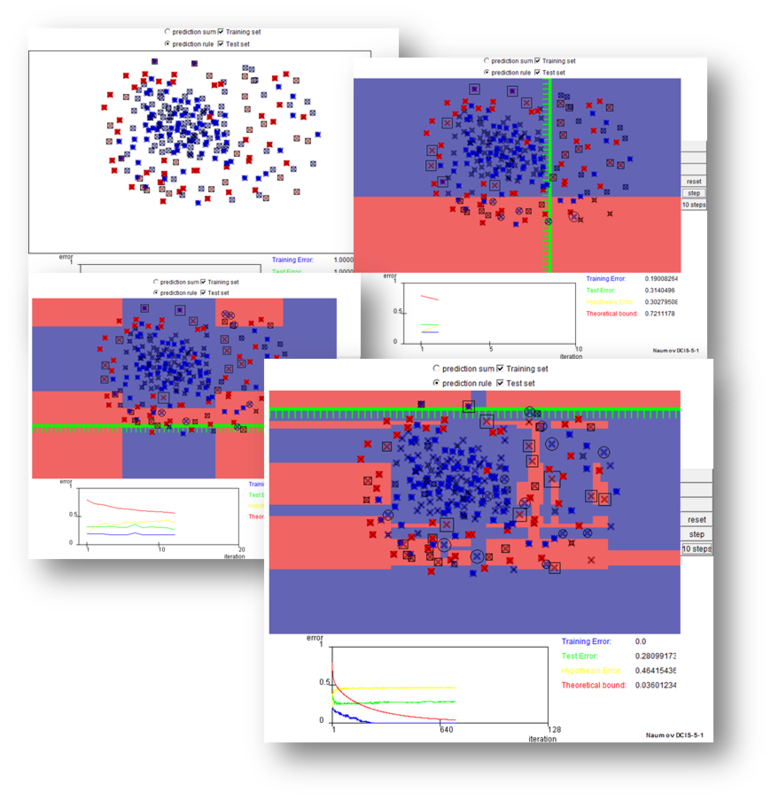
AdaBoost लाभ:

अच्छी सामान्यीकरण क्षमता। वास्तविक जीवन की समस्याओं में, बुनियादी एल्गोरिदम की गुणवत्ता में श्रेष्ठ रचनाएँ लगभग हमेशा निर्मित होती हैं। सामान्य एल्गोरिदम की संख्या बढ़ने पर सामान्यीकरण क्षमता में सुधार हो सकता है;
कार्यान्वयन में आसानी;
बूस्टिंग का अपना ओवरहेड छोटा होता है। किसी रचना का निर्माण करने का समय लगभग पूरी तरह से उस समय तक निर्धारित होता है, जिसमें बुनियादी एल्गोरिदम सीखने में समय लगता है;
ध्वनि उत्सर्जन की वस्तुओं की पहचान करने की क्षमता। ये सबसे "मुश्किल" वस्तुएं हैं x _i , जिसके लिए, संरचना के निर्माण की प्रक्रिया में, सबसे अधिक मानों को तौलता है।

AdaBoost विपक्ष:

डेटा में एक महत्वपूर्ण शोर स्तर की उपस्थिति में रिट्रेनिंग है। घातीय नुकसान फ़ंक्शन "सबसे कठिन" वस्तुओं के वजन को बहुत अधिक बढ़ाता है, जिस पर कई बुनियादी एल्गोरिदम गलत हैं। हालांकि, यह ऐसी वस्तुएं हैं जो अक्सर शोर उत्सर्जन के रूप में निकलती हैं। नतीजतन, AdaBoost शोर करने के लिए ट्यून करना शुरू कर देता है, जो पीछे हटने की ओर जाता है। समस्या को उत्सर्जन को हटाकर या कम "आक्रामक" नुकसान कार्यों का उपयोग करके हल किया जाता है। विशेष रूप से, जेंटलबॉस्ट एल्गोरिथ्म का उपयोग किया जाता है;
AdaBoost को पर्याप्त रूप से लंबे प्रशिक्षण नमूनों की आवश्यकता होती है। अन्य रैखिक सुधार विधियां, विशेष रूप से बैगिंग में, छोटे डेटा नमूनों से तुलनीय गुणवत्ता के एल्गोरिदम का निर्माण करने में सक्षम हैं;
बुनियादी एल्गोरिदम के गैर-इष्टतम सेट का निर्माण होता है। रचना को बेहतर बनाने के लिए, आप समय-समय पर पहले से निर्मित एल्गोरिदम पर लौट सकते हैं और उन्हें फिर से प्रशिक्षित कर सकते हैं।
बूस्टिंग सैकड़ों एल्गोरिदम से मिलकर भारी रचनाओं का निर्माण कर सकती है। इस तरह की रचनाएं एक सार्थक व्याख्या की संभावना को बाहर करती हैं, बुनियादी एल्गोरिदम को संग्रहीत करने के लिए बड़ी मात्रा में स्मृति की आवश्यकता होती है और वर्गीकरण की गणना पर महत्वपूर्ण समय खर्च होता है।

आजकल, सरल क्लासिफायर को मजबूत करने का दृष्टिकोण एक लोकप्रिय और संभवत: काम की उच्च गति और दक्षता और कार्यान्वयन की सापेक्ष आसानी के कारण सबसे प्रभावी वर्गीकरण विधि है।

विकसित एल्गोरिदम में निर्णय के पेड़ के सिद्धांत

निर्णय वृक्ष एक पेड़ है जिसकी पत्तियों में वस्तुनिष्ठ फ़ंक्शन के मान हैं, और अन्य नोड्स में संक्रमण की स्थिति है (उदाहरण के लिए, चेहरे पर एक मुस्कुराहट है) जो यह निर्धारित करती है कि किस किनारे पर जाना है। यदि इस अवलोकन के लिए स्थिति सही है, तो झूठ को किनारे पर ले जाया जाता है, अगर झूठ दाईं ओर है [4]। उदाहरण के लिए, पेड़ को निम्नलिखित आकृति में दिखाया गया है:

निर्णय वृक्ष बनाने के लिए एक उदाहरण एल्गोरिथ्म नीचे दिया गया है:

function Node = _( {(x,y)} ) {
if {y}
return _(y);
test = __( {(x,y)} );
{(x0,y0)} = {(x,y) | test(x) = 0};
{(x1,y1)} = {(x,y) | test(x) = 1};
LeftChild = _( {(x0,y0)} );
RightChild = _( {(x1,y1)} );
return _(test, LeftChild, RightChild);
}
//
function main() {
{(X,Y)} = __();
TreeRoot = _( {(X,Y)} );
}

ऐसे निर्णायक पेड़ों के फायदे दृश्यता हैं, उनके साथ काम में आसानी, गति। इसके अलावा, वे कई वर्गों के साथ कार्यों के लिए आवेदन करना आसान है।

विकसित एल्गोरिथम का कैस्केड मॉडल

मेरे दृष्टिकोण से चेहरे को खोजने के लिए बूस्टिंग एल्गोरिथ्म इस प्रकार है:
1. आयताकार संकेतों के लिए कमजोर क्लासिफायर की परिभाषा;
2. स्कैनिंग विंडो के प्रत्येक आंदोलन के लिए, प्रत्येक उदाहरण पर एक आयताकार विशेषता की गणना की जाती है;
3. प्रत्येक सुविधा के लिए सबसे उपयुक्त सीमा का चयन किया जाता है;
4. सबसे अच्छे संकेत और सर्वोत्तम उपयुक्त सीमा का चयन किया जाता है;
5. नमूना reweighed है।

– , , , . , , , . , .
, , . :

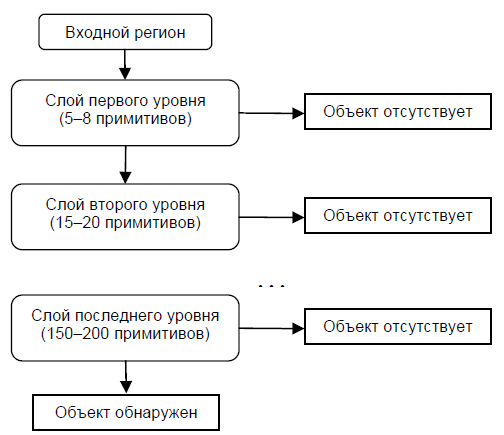
(xyz), x , y z .
, :
1. «» – «» ;
2. , ;
3. , ;
4. , .

:
1. ( ) – detection false positive rates – detection , false positive rates ;
2. , , , :
एक। ;
ख। AdaBoost , ;
3. false positive rates , ;
4. .

:

a) f ( ) d ( )
b) F _target
c) P –
d) N –
e) F ₀ = 1,0; D ₀ = 1,0; i = 0
f) while ( F _i > F _target )
i = i+1; n _i = 0; F _i = F _i-1
while (F _i = f * F _i-1 )
n _i = n _i + 1
AdaBoost(P, N, n _i )
F _i D _i ;
i- , d*D _i -1 ( F _i ) ;
g) N = Ø;
h) F _i > F _target , , , N.

निष्कर्ष

- (Viola-Jones). , — .

संदर्भ:

1. P. Viola and MJ Jones, «Rapid Object Detection using a Boosted Cascade of Simple Features», proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR 2001), 2001
2. P. Viola and MJ Jones, «Robust real-time face detection», International Journal of Computer Vision, vol. 57, no. 2, 2004., pp.137–154
3. ., ., « », ISBN 5-94836-028-8, -: , , 2005. – 1072 .
4. . ., « », , , , 2002–2004., . 42 – 44
5. Jan ˇSochman, Jiˇr´ı Matas, «AdaBoost», Center for Machine Perception, Czech Technical University, Prague, 2010
6. Yoav Freund, Robert E. Schapire, «A Short Introduction to Boosting», Shannon Laboratory, USA, 1999., pp. 771-780

PS , , 2 , , . !

चेहरे की पहचान के लिए आधार के रूप में वायोला-जोन्स विधि