🔹 🧦 🎑 एक तारकीय क्षेत्र के रोटेशन के केंद्र की गणना करने के लिए ऑक्टेव का उपयोग करना 📰 👨🏿‍🌾 👩🏻‍🎓

मैंने पहले ही ऑक्टेव में FITS फाइलों के साथ काम करने के बारे में आंशिक रूप से बात की है । अब मैं विशिष्ट डेटा को संसाधित करने के लिए इस गणितीय पैकेज के आवेदन के बारे में बात करूँगा, अर्थात्: एक निश्चित अंतराल के साथ प्राप्त छवियों के सेट से एक तारकीय क्षेत्र के रोटेशन के केंद्र की गणना करने के लिए।

ज्यामितीय परिवर्तन

एक शुरुआत के लिए, आइए गणितीय भाग पर स्पर्श करें। वेक्टर-मैट्रिक्स रूप में गणितीय रूप से ज्यामितीय परिवर्तनों का प्रतिनिधित्व करना सुविधाजनक है। इसलिए, उदाहरण के लिए, यदि हमारे पास एक त्रिज्या वेक्टर है जो किसी दिए गए छवि बिंदु को चिह्नित करता है, तो एक प्रदर्शन बिंदु के त्रिज्या वेक्टर को प्राप्त करने के लिए, r ' r : r' = A · r द्वारा आपको ज्यामितीय परिवर्तन मैट्रिक्स, ए को गुणा करना होगा। सरलतम मामले में, ए दो-आयामी 2x2 मैट्रिक्स है। हालांकि, जटिल परिवर्तनों के लिए इसे 3x3 आयामों तक विस्तारित करने की आवश्यकता है: उदाहरण के लिए, छवि विस्थापन का वर्णन करने के लिए।

सामान्य स्थिति में, वैक्टर आर और आर ' तीन तत्वों के कॉलम वैक्टर हैं: बिंदु और इकाई के निर्देशांक। 3x3 परिवर्तन मैट्रिक्स में केवल छह महत्वपूर्ण तत्व (ऊपरी दो पंक्तियाँ) हैं, और इसकी तीसरी पंक्ति में दो शून्य और एक इकाई है।
इस मामले में, मैट्रिक्स रूप में कोण matrix द्वारा मूल के सापेक्ष रोटेशन का परिवर्तन इस प्रकार लिखा जाता है:

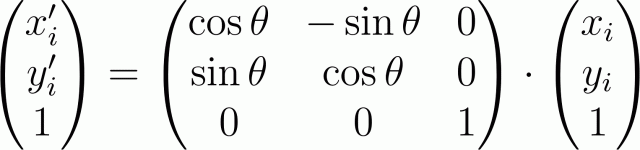
ज्यामितीय परिवर्तन मैट्रिक्स के महत्वपूर्ण सदस्यों के निम्नलिखित अर्थ हैं: ऊपरी बाएं कोने का 2x2 सबमेट्रिक्स रूपांतरणों को दर्शाता है जो बिंदु के निर्देशांक (उदाहरण के लिए, रोटेशन, स्केलिंग) पर निर्भर करता है, और सबसे दाईं ओर के ऊपरी दो सदस्य परिवर्तनों का प्रतिनिधित्व करते हैं जो निर्देशांक (ऑफसेट) पर निर्भर नहीं होते हैं।

इस प्रकार, उदाहरण के लिए, एक कोण पर उत्पत्ति के चारों ओर रोटेशन मैट्रिक्स, वेक्टर टी द्वारा इस बदलाव के बाद ऐसा दिखेगा:

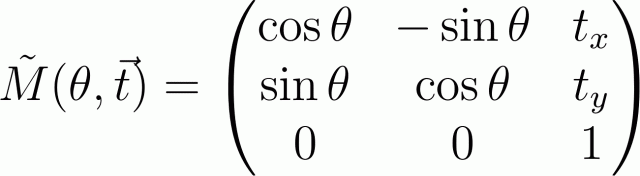
अधिक जटिल परिवर्तन का वर्णन करने वाले एक मैट्रिक्स को प्राप्त करने के लिए, हमें इस गति को प्राथमिक लोगों (रोटेशन, विस्थापन, स्केलिंग) में विघटित करना होगा और संबंधित मैट्रिक्स को गुणा करना होगा। जिन लोगों ने ओपनजीएल के साथ काम किया है, उन्हें ऐसा करने में कोई परेशानी नहीं होगी। केवल यह याद रखना आवश्यक है कि यदि परिवर्तन A, B, C के क्रम में किए जाते हैं, तो उन्हें "पीछे की ओर" गुणा करना होगा: परिणामस्वरूप मैट्रिक्स M = C · B · A (क्योंकि परिवर्तन A पहली बार A · r के गुणन द्वारा किया जाता है, परिणामस्वरूप वेक्टर परिवर्तन बी और इतने पर से गुजरता है।

एक मनमाना बिंदु के चारों ओर घूमना तीन प्राथमिक परिवर्तनों में विघटित हो जाता है: छवि को स्थानांतरित करना ताकि मूल रोटेशन बिंदु पर हो (यानी यदि रोटेशन का केंद्र बिंदु (x, y) पर है, तो आपको इसे वेक्टर (-x, -y) द्वारा स्थानांतरित करने की आवश्यकता है) ; कोण θ और रिवर्स शिफ्ट द्वारा वेक्टर (x, y) द्वारा इसका रोटेशन। इस गुणन के परिणामस्वरूप, परिवर्तन मैट्रिक्स का रूप होगा

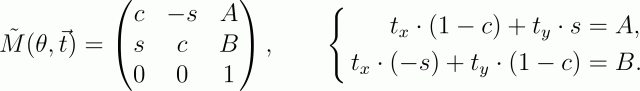
(अंकन को सरल बनाने के लिए, मैंने पाप sin को s और cos c के साथ c) से बदल दिया।

यदि हम मैट्रिक्स आर के रूप में रोटेशन मैट्रिक्स के महत्वपूर्ण शब्दों को निरूपित करते हैं, तो समीकरणों की अंतिम प्रणाली को मैट्रिक्स रूप (IR) · t = AB में दर्शाया जा सकता है, जहां AB अंतिम परिवर्तन मैट्रिक्स के ए और बी से कॉलम वेक्टर है।
यहां से आप वेक्टर टी को छवि के केंद्र को चिह्नित कर पा सकते हैं: t = (IR) \ AB , जहां बैकस्लैश "बाएं" डिवीजन (मैटलाब और ऑक्टेव द्वारा अपनाई गई प्रविष्टि) के संचालन को दर्शाता है: बीजगणित में, यह नोटेशन t = (IR) ^{-1 के समान है} एबी ( मैं पहचान मैट्रिक्स हूं )।

यदि रोटेशन छोटे विस्थापन के साथ होता है, तो वेक्टर AB में एडिटिव टर्म ड्र शामिल होगा, जो गणना में एक महत्वपूर्ण त्रुटि का परिचय देगा (चूंकि छोटे कोणों के माध्यम से घूर्णन करते समय वेक्टर एबी का रोटेशन छोटा होता है)। इस विस्थापन को गणितीय रूप से निर्धारित करना असंभव है, केवल हाथ में कुछ जोड़े हैं। हालांकि, अगर हमारे पास महत्वपूर्ण संख्या में चित्र हैं, तो हम रोटेशन के केंद्र के औसत मूल्य की गणना कर सकते हैं, और इसे जानने से पहले ही छोटे विस्थापन को निर्धारित करना आसान होगा।

ऑक्टेव में कार्यान्वयन

तो, हमारे पास स्टार फ़ील्ड की छवियों का एक सेट है (यह, वैसे, मज़बूती से प्रतिष्ठित संदर्भ क्षेत्रों के साथ एक मनमानी छवि हो सकती है) और इस क्षेत्र के रोटेशन के केंद्र की गणना करना आवश्यक है।

शुरू करने के लिए, हमें सितारों (सामान्य स्थिति, संदर्भ बिंदुओं) का चयन करने की आवश्यकता है। विशिष्ट मामले में, यह किसी दिए गए सीमा पर सरल द्वैतकरण द्वारा हल किया जाता है (थ्रेशोल्ड को उपयोगकर्ता द्वारा निर्दिष्ट मूल्य के अधिकतम के रूप में चुना जाता है और छवि में औसत दर्जे के तीव्रता मानों का योग प्लस मानक विचलन का एक चौथाई)। इसके अलावा, परिणामस्वरूप द्विआधारी छवि में, 8-कनेक्टिविटी के साथ क्षेत्रों का पता लगाया जाता है और पता लगाने के क्रम में क्रमांकित किया जाता है। नतीजतन, हमें मास्क का एक सेट मिलता है जिसके साथ आप वस्तुओं के केंद्रों की गणना कर सकते हैं (सरलतम मामले में, गुरुत्वाकर्षण के प्राथमिक केंद्र के रूप में)।

अगला, हमें उन वस्तुओं को उजागर करने की आवश्यकता है जो सभी छवियों में मौजूद हैं। मैंने इस समस्या को "हेड-ऑन" हल किया: प्रत्येक छवि के लिए वैक्टर का एक सेट का निर्माण किया जाता है - प्रत्येक वस्तु के सापेक्ष ध्रुवीय प्रणाली में ज्ञात वस्तुओं के निर्देशांक (जो कि एन बिंदुओं के एक सेट के लिए हमें एन · (एन -1) वेक्टर मिलते हैं)। पहचान के लिए, पहली और i-th छवि के लिए वैक्टर के सभी सेट को क्रमबद्ध किया जाता है। प्रत्येक सेट को एक अनुमान दिया जाता है - उपयोगकर्ता द्वारा परिभाषित त्रुटि dr, d defined तक के बिंदुओं के त्रिज्या वैक्टर के संयोग की संख्या। तब उच्चतम रेटिंग वाले सेटों की एक जोड़ी का चयन किया जाता है और पहली छवि के ऑब्जेक्ट्स के क्रम के अनुसार आई-वें छवि की वस्तुओं को गिना जाता है। पहली छवि की वस्तुओं का पता लगाने के लिए प्रत्येक प्रक्रिया के बाद, पहली छवि की पहचान की गई वस्तुओं के अनुरूप काउंटरों का मान ith मूल्य पर बढ़ता है। समानांतर में, ज्ञात वस्तुओं के निर्देशांक संचित होते हैं।

यह "हेड-ऑन" समाधान गणनाओं को बहुत धीमा कर देता है और बड़ी संख्या में पता चला वस्तुओं और बड़ी संख्या में छवियों के मामले में बहुत अधिक मेमोरी का उपभोग करता है, इसलिए विधि को सरल बनाया जा सकता है। उदाहरण के लिए, आप पहले और अंतिम छवि की तुलना कर सकते हैं, अंक के एक सेट पर निर्णय लिया है (जो मेमोरी की खपत और पुनरावृत्तियों की संख्या को कम करेगा); पहली छवि की केवल दो या तीन वस्तुओं के संबंध में ही खोज की जा सकती है (केवल एक सेट की तुलना का उपयोग करना असंभव है, क्योंकि एक विशिष्ट वस्तु को ith छवि में नहीं पाया जा सकता है)।

वस्तुओं की खोज के बाद, हमें काउंटरों की एक सरणी मिलती है। यदि ऑब्जेक्ट सभी छवियों में मौजूद है, तो संबंधित काउंटर का मान M-1 के बराबर होना चाहिए (M छवियों की संख्या है)। वह सभी डेटा जिसके लिए काउंटर M-1 के बराबर नहीं है, हटा दिया गया है। अगला, आपको केवल जोड़े में सभी छवियों के लिए वस्तुओं के निर्देशांक की तुलना करने की आवश्यकता है, उपरोक्त सूत्र का उपयोग करके प्रत्येक जोड़ी के लिए रोटेशन के केंद्र की गणना करना (परिवर्तन मैट्रिक्स की गणना सबसे कम वर्गों द्वारा की जाती है)। केंद्र निर्देशांक की एक सरणी संचित होने के बाद, हम सभी निर्देशांक के मध्य के रूप में रोटेशन का वास्तविक केंद्र पाते हैं।

अपनी विधि के अलावा, मुझे इस लेख में एक और विधि मिली (मैककेन एट अल।)। यह विधि सुविधाजनक है कि इसे कम से कम चौकोर विधि द्वारा परिवर्तन मैट्रिक्स को खोजने की आवश्यकता नहीं है। यह इस तथ्य पर आधारित है कि एक मनमाना बिंदु के चारों ओर रोटेशन को अधिक सरल रूप से दर्शाया जा सकता है: मूल के सापेक्ष रोटेशन और बाद में विस्थापन। लेखकों ने पूरे सिस्टम के रोटेशन के कोण को निर्धारित करने के लिए परिवर्तन मैट्रिक्स की गणना करने के बजाय प्रस्तावित किया (जो कि वस्तुओं के गुरुत्वाकर्षण के केंद्र के सापेक्ष ध्रुवीय समन्वय प्रणाली में वस्तुओं के निर्देशांक के प्रतिनिधित्व का उपयोग करना आसान है)। रोटेशन कोण से, रोटेशन मैट्रिक्स आर की गणना की जाती है। पहली छवि की वस्तुओं के त्रिज्या वैक्टर द्वारा इस मैट्रिक्स को गुणा करते हुए, हम विस्थापन वेक्टर, v (i-वें छवि की वस्तुओं के त्रिज्या वैक्टर के अंतर के मध्य और प्राप्त त्रिज्या वैक्टर के रूप में) पाते हैं। रोटेशन के केंद्र की गणना समान सूत्र t = (IR) ^-1 v का उपयोग करके की जाती है।

बड़ी मात्रा में सांख्यिकीय सामग्री पर, दोनों विधियों ने समान परिणाम दिए। एक विधि या किसी अन्य की पसंद कार्यान्वयन द्वारा निर्धारित की जाती है: ओक्टेव में, उदाहरण के लिए, मेरी विधि की गणना तेजी से की जाती है, और दोनों विधियों का कार्यान्वयन सरल है; एल्गोरिथ्म को C में लागू करते समय, McKein टीम के साथी का रास्ता आसान हो जाएगा।

यहां केंद्रों के पाया निर्देशांक बिखरा हुआ है:

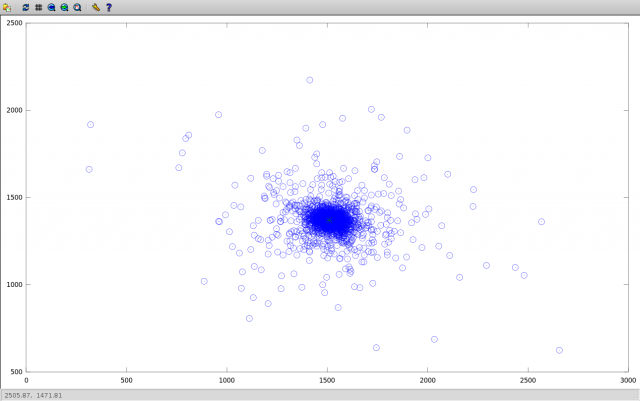
आउटलेर्स को इस तथ्य से समझाया जाता है कि पड़ोसी छवियों की तुलना करते समय (जिसके लिए रोटेशन कोण छोटा है) हमें विस्थापन की गणना में एक बहुत ही उच्च त्रुटि मिलती है, वस्तुओं के निर्देशांक की गणना करने में त्रुटि के बराबर। मध्यिका के सापेक्ष पाए जाने वाले निर्देशांक का पूर्ण विचलन ऊपर दर्शाया गया है:

(करीब छवियों के उत्सर्जन विशिष्ट तो तेजी से रोटेशन कोण के साथ कमी)। मेडियन औसत आपको इन आउटलेयर को छोड़ने की अनुमति देता है।

हां, मैं लगभग एक स्टार फील्ड की छवि का उदाहरण देना भूल गया। यहाँ यह है:

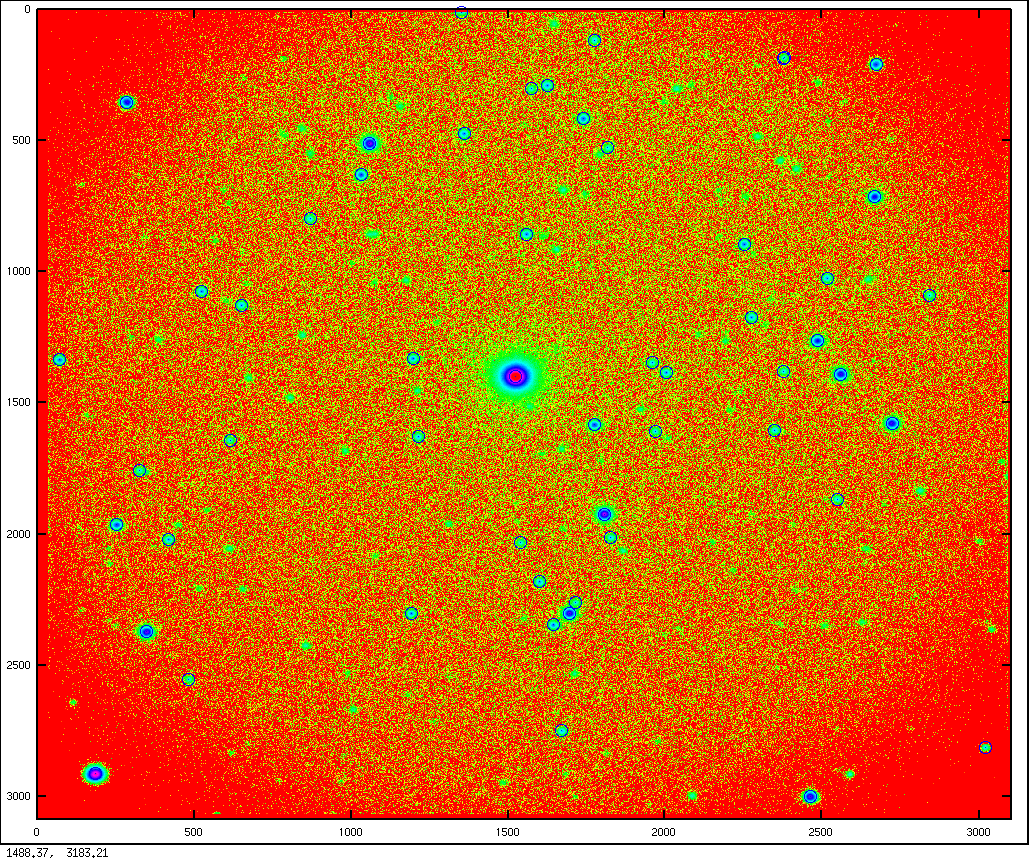
स्रोत कोड

FITS फाइलें पढ़ना:

function [image header] = fits_read(filename) % %  FITS-      %  y    ! % (   flipdim,   ) % % : % read_fits_image (  fits) % image = []; printf("Read file %s ... ", filename); fflush(1); % ,         : [ sem ] = stat(filename); if(e != 0 || !S_ISREG(s.mode)) printf("No such file!\n"); fflush(1); return; endif [ image header ] = read_fits_image(filename); if(!isempty(image)) image = flipdim(image',1); % ,    printf("OK!\n"); else printf("Bad image!\n"); endif fflush(1); endfunction

वस्तुओं के केंद्रों की गणना:

 function [ xc, yc ] = find_centers(Img, treshold) % [ xc, yc ] = find_centers(Img, treshold) %     Img    treshold % xc, yc -   % tmp = zeros(size(Img)); mm = mean2(Img) + std2(Img)/4; %    tres1 = max(mm, treshold); printf("\nTreshold: %g\n", tres1); fflush(stdout); tmp(find(Img > tres1)) = 1; tmp = medfilt2(logical(tmp)); [ Labels, Nlabels ] = bwlabel(tmp); if(Nlabels < 1) printf(stderr, "\nError! There's no spots!!!\n\n"); return endif [yy, xx] = ndgrid(1:size(Img,1),1:size(Img,2)); xc = []; yc = []; for i = [1 : Nlabels] idxs = find(Labels == i); Is = sum(Img(idxs)); xc = [ xc sum(Img(idxs) .* xx(idxs)) / Is ]; yc = [ yc sum(Img(idxs) .* yy(idxs)) / Is ]; end endfunction

ऑब्जेक्ट नंबर N के सापेक्ष वस्तुओं के निर्देशांक की गणना:

 function coords = find_tree(xc, yc, N) % % coords = find_tree(xc, yc, N) %     , xc  yc,     %   N       . %  ,     -   % ,  -  . % if(size(xc, 1)) == 1 % ,      xc = xc'; endif if(size(yc, 1)) == 1 yc = yc'; endif if(size(xc) != size(yc) || N > size(xc, 1)) %   coords = []; endif xn = xc(N); yn = yc(N); %  N-  Dx = xc - xn; Dy = yc - yn; %     N- R = sqrt(Dx.^2+Dy.^2); %   Phi = atan2(Dy,Dx)*180/pi; %   coords = [R Phi]; endfunction

किसी दिए गए चित्र के लिए वस्तुओं के सभी सापेक्ष निर्देशांक का एक सेट बनाना:

 function [Tree xc yc] = get_tree(treshold, i) % % [Tree xc yc] = get_tree(treshold, i) %            % : % treshold -      % i -     % : % Tree -      ,   % *   -      % *   -       % *   -      % xc, yc -   % % : % fits_read % find_tree % find_centers % Tree = []; xc = []; yc = []; name = sprintf("object_%04d.fit", i); II = fits_read(name); if(isempty(II)) return; endif printf("Find centers of %s ... ", name); fflush(1); [xc, yc] = find_centers(II, treshold); for j = 1:size(xc,2) Tree(:,:,j) = find_tree(xc, yc, j); endfor printf("done (%d vectors)!\n", size(Tree, 1)); endfunction

दो छवियों पर वस्तु संख्याओं का पत्राचार प्राप्त करना:

 function coord_indexes = find_cluster_c(CC, CC1, dR, dPhi) % % coord_indexes = find_cluster_c(CC, CC1, dR, dPhi) %      CC   CC1 % : % CC, CC1 -       % dR -   R ( |r1-r0| < dR, ,  r1 == r0) % dPhi -      % : % coord_indexes -      [1 2; ...] % Ncc = size(CC, 3); Ncc1 = size(CC1, 3); % -      Cluster = []; %   : - , 1, 2,   for jj = 1 : Ncc %      Nnear = []; % ,     -      PhiMed = []; %    r0 = CC(:,1,jj); phi0 = CC(:,2,jj); for ii = 1 : Ncc1 %      r1 = CC1(:,1,ii); phi1 = CC1(:,2,ii); points = {}; %      (  1;     2) dphi_s = []; % ,         for i = 1:size(r0); %      d = abs(r1-r0(i)); %    idx = find(d < dR); %     r if(isempty(idx)) continue; endif; %   -   points = [ points; {i, idx} ]; %     endfor for i = 1:size(points, 1) dphi = abs(phi1(points{i,2}) - phi0(points{i,1})); dphi_s = [dphi_s; dphi]; endfor if(isempty(dphi_s)) continue; endif; dphi = median(dphi_s); %     2  1 n = size(find(abs(dphi_s-dphi)<dPhi), 1); Nnear = [ Nnear, n ]; %   PhiMed = [ PhiMed, dphi ]; endfor idx = find(Nnear == max(Nnear))(1); %   ,    jj- Cluster = [ Cluster; Nnear(idx) jj idx PhiMed(idx) ]; endfor %       n = max(Cluster(:,1)); %   idx = find(Cluster(:,1) == n)(1); %       first = Cluster(idx, 2); %     1 second = Cluster(idx, 3); % -//- 2 Phi = Cluster(idx, 4); %   2  1 r0 = CC(:,1,first); phi0 = CC(:,2,first); r1 = CC1(:,1,second); phi1 = CC1(:,2,second); coord_indexes = []; for i = 1:size(r0); %      d = abs(r1-r0(i)); %    idx = find(d < dR); %     r if(isempty(idx)) continue; endif; %   -   dphi = abs(abs(phi1(idx) - phi0(i)) - Phi); if(size(idx, 1) != 1) %   n = find(dphi == min(dphi))(1); %     idx = idx(n); dphi = dphi(n); endif if(dphi > dPhi) continue; endif; %   -   coord_indexes = [ coord_indexes; i idx ]; endfor endfunction

पहली छवि पर उनकी संख्या के अनुसार सभी छवियों पर वस्तुओं के निर्देशांक के सरणियों को प्राप्त करना:

 function [XY] = get_centers(i0, i1, treshold, dR, dPhi) % % [XY] = get_centers(i0, i1, treshold, dR, dPhi) %    X,Y       %  % : % i1, in -      % treshold -     % dR, dPhi -     (   ) % : % X, Y -      %         %   -   %     -       % % : % get_tree -> fits_read, find_tree, find_centers % find_cluster_c % n = 1; %   +     X,Y i_start = i0; %      CS = []; printf("\nimage 1\n", i); do [CC xc yc] = get_tree(treshold, i_start); im1 = i_start; i_start++; until(!isempty(CC) || i_start > i1) X = xc'; Y = yc'; %   -   Counters = zeros(size(X)); %       for i = i_start:i1 [CC1 xc1 yc1] = get_tree(treshold, i); if(isempty(CC1)) continue; endif printf("\nimage %d, ", ++n); %       indexes = find_cluster_c(CC, CC1, dR, dPhi); printf("%d points\n\n", size(indexes, 1)); %  : X(indexes(:,1),n) = xc1(indexes(:,2)); Y(indexes(:,1),n) = yc1(indexes(:,2)); %       Counters(indexes(:,1))++; endfor %  ,      idx = find(Counters != n-1); X(idx,:) = []; Y(idx,:) = []; endfunction

रोटेशन का केंद्र हो रहा है:

 function [Xc Yc] = matr_center(X, Y) % % [Xc Yc] = matr_center(X, Y) %    ,     % : % X, Y -     (  get_centers) % : % Xc, Yc -    % Xc = []; Yc = []; imax = size(X,2); for i = 1:imax-1 for j = i+1:imax %    X0 = X(:,i)'; X1 = X(:,j)'; Y0 = Y(:,i)'; Y1 = Y(:,j)'; %      ( -   ) vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0); vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1); %    ,        %phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X); %%    2,    -pi+a -> pi-b %phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi; %dphi = median(phi1 - phi0); %     %R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; %   %RR1 = R * [vec0X;vec0Y]; % ,       0 %dR = sqrt((vec1X-RR1(1,:)).^2+(vec1Y-RR1(2,:)).^2); %      %idx = find(dR < median(dR)+std(dR)); %    %if(size(idx,2) < 3) %    %printf("Image %d: too much bad data\n", i); %continue; %endif %X0 = X0(idx); X1 = X1(idx);Y0 = Y0(idx); Y1 = Y1(idx); %     A = [X1;Y1;ones(size(X1))]/[X0;Y0;ones(size(X1))]; %     CRDS = (eye(2)-A(1:2,1:2)) \ A(1:2,3); Xc = [Xc CRDS(1)]; Yc = [Yc CRDS(2)]; %   endfor endfor Xmed = median(Xc) Ymed = median(Yc) endfunction

वही, लेकिन मैककेन एसोसिएट्स विधि द्वारा:

 function [Xc Yc] = matr_center_notmine(X, Y) % % [Xc Yc] = matr_center(X, Y) %    ,     % : % X, Y -     (  get_centers) % : % Xc, Yc -    % Xc = []; Yc = []; imax = size(X,2); for i = 1:imax-1 for j = i+1:imax %    X0 = X(:,i)'; X1 = X(:,j)'; Y0 = Y(:,i)'; Y1 = Y(:,j)'; %      ( -   ) vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0); vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1); phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X); %    2,    -pi+a -> pi-b phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi; dphi = median(phi1 - phi0); %     R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; %   %   v v = median(R * [X0; Y0] - [X1; Y1], 2); %     CRDS = (eye(2)-R) \ v; %printf("Center: (%g, %g)\n", CRDS(1), CRDS(2)); Xc = [Xc -CRDS(1)]; Yc = [Yc -CRDS(2)]; %   endfor endfor Xmed = median(Xc) Ymed = median(Yc) endfunction

एक तारकीय क्षेत्र के रोटेशन के केंद्र की गणना करने के लिए ऑक्टेव का उपयोग करना

ज्यामितीय परिवर्तन

ऑक्टेव में कार्यान्वयन

स्रोत कोड

More articles: