परिचय
[1]एक भग्न (अव्य। "फ्रैक्टस" - कुचल, टूटा हुआ, टूटा हुआ) आत्म-समानता की संपत्ति के साथ एक जटिल ज्यामितीय आकृति है, अर्थात। कई भागों से बना है, जिनमें से प्रत्येक पूरे आंकड़े के समान है। एक व्यापक अर्थ में, फ्रैक्टल का मतलब यूक्लिडियन अंतरिक्ष में बिंदुओं के सेट होते हैं जिनमें एक मध्यवर्ती (आंशिक) मीट्रिक आयाम (हॉसडॉर्फ आयाम) होता है।
मीट्रिक अंतरिक्ष में सेट के आयाम को निर्धारित करने के लिए हॉसडॉर्फ आयाम एक प्राकृतिक तरीका है। हौसडॉर्फ आयाम उन मामलों में आयाम की हमारी सामान्य धारणाओं के अनुरूप है जहां ये साधारण धारणाएं मौजूद हैं। उदाहरण के लिए, तीन-आयामी यूक्लिडियन अंतरिक्ष में, एक परिमित सेट का हॉसडॉर्फ़ आयाम शून्य है, एक चिकनी वक्र का आयाम एक है, एक चिकनी सतह का आयाम दो है और नोज़ेरो वॉल्यूम के एक सेट का आयाम तीन है।
भग्न कई प्रकार के होते हैं:
- ज्यामितीय भग्न भग्न का सबसे दृश्य वर्ग है। दो-आयामी अंतरिक्ष में, उन्हें कुछ टूटी हुई रेखा (या तीन-आयामी अंतरिक्ष में सतह) की सहायता से प्राप्त किया जाता है, जिसे एक जनरेटर कहा जाता है। एल्गोरिथ्म के एक चरण में, धनुष-तरंग बनाने वाले प्रत्येक सेगमेंट को टूटी-रेखा जनरेटर द्वारा एक उपयुक्त पैमाने पर बदल दिया जाता है। इस प्रक्रिया के अंतहीन दोहराव के परिणामस्वरूप, एक ज्यामितीय भग्न प्राप्त होता है।
- बीजगणितीय भग्न भग्न का सबसे बड़ा समूह है। वे एन-डायमेंशनल स्पेस में नॉनलाइनियर प्रक्रियाओं का उपयोग करके प्राप्त किए जाते हैं। द्वि-आयामी प्रक्रियाएं सबसे अधिक अध्ययन की जाती हैं। असतत गतिशील प्रणाली के रूप में एक नॉनलाइनियर पुनरावृत्ति प्रक्रिया की व्याख्या करना, कोई इन प्रणालियों के सिद्धांत की शब्दावली का उपयोग कर सकता है: चरण चित्र, स्थिर राज्य प्रक्रिया, अट्रैक्टर, आदि। यह ज्ञात है कि nonlinear डायनेमिक सिस्टम में कई स्थिर अवस्थाएँ होती हैं। जिस राज्य में डायनेमिक सिस्टम एक निश्चित संख्या में पुनरावृत्तियों के बाद खुद को पाता है वह अपनी प्रारंभिक स्थिति पर निर्भर करता है। इसलिए, प्रत्येक स्थिर स्थिति (या, जैसा कि वे कहते हैं, एक आकर्षित करने वाला) के पास प्रारंभिक राज्यों का एक निश्चित क्षेत्र है, जहां से सिस्टम आवश्यक रूप से विचार के तहत अंतिम राज्यों में गिर जाएगा। इस प्रकार, सिस्टम के चरण स्थान को आकर्षण के क्षेत्र में विभाजित किया जाता है। यदि चरण स्थान एक दो-आयामी स्थान है, तो विभिन्न रंगों के साथ आकर्षण के क्षेत्रों को रंगकर, आप इस प्रणाली (पुनरावृत्ति प्रक्रिया) का एक रंग चरण चित्र प्राप्त कर सकते हैं। रंग चयन एल्गोरिथ्म को बदलकर, आप फैंसी बहु-रंग पैटर्न के साथ जटिल भग्न पैटर्न प्राप्त कर सकते हैं। गणितज्ञों के लिए आश्चर्य की बात यह थी कि बहुत जटिल गैर-तुच्छ संरचनाओं को उत्पन्न करने के लिए आदिम एल्गोरिदम का उपयोग करने की संभावना थी।
- स्टोचैस्टिक फ्रैक्टल्स फ्रैक्टल्स का एक और जाना-माना वर्ग है, जो प्राप्त होता है यदि पुनरावृत्ति प्रक्रिया में इसके किसी भी पैरामीटर को बेतरतीब ढंग से बदल दिया जाता है। यह प्राकृतिक वस्तुओं के समान वस्तुओं का उत्पादन करता है - विषम पेड़, बीहड़ समुद्र तट आदि। इलाके और समुद्र की सतह को मॉडल करने के लिए दो आयामी स्टोकेस्टिक फ्रैक्टल का उपयोग किया जाता है।
इनके अतिरिक्त, ये भी हैं:
- मानव निर्मित भग्न
- प्राकृतिक फ्रैक्चर
- नियतात्मक भग्न
- गैर-निर्धारक भग्न
इस लेख के ढांचे में, हम इन भग्न बनाने के तरीकों पर विचार करेंगे: एल-सिस्टम और पुनरावृत्त कार्यों की प्रणाली।
1. Iterated फ़ंक्शन सिस्टम
परंपरागत रूप से गणित में, रिक्त स्थान और सेट में अंक होते हैं। हालांकि, ऐसे स्थान हैं जिनमें "अंक" स्वयं सेट होते हैं। गणितीय दृष्टिकोण से, एक बिंदु से अमूर्तता की गरिमा समानता को प्राप्त करना है।
इसका एक उदाहरण है संकुचन मैपिंग और संबंधित अभिसरण सिद्धांत। संपीड़न मैपिंग को मीट्रिक रिक्त स्थान में मैपिंग के रूप में परिभाषित किया जाता है जो अंकों के बीच की दूरी को कम करते हैं। संपीड़न मैपिंग में एक महत्वपूर्ण संपत्ति है। यदि हम कोई बिंदु लेते हैं और पुनरावृत्ति को उसी संकुचन मानचित्र पर लागू करना शुरू करते हैं: f (f (f (f ... f (x))), तो परिणाम हमेशा एक ही बिंदु होगा। जितना अधिक बार हम आवेदन करेंगे, उतने ही सटीक रूप से हम इस बिंदु को पाएंगे। इसे एक निश्चित बिंदु कहा जाता है और प्रत्येक कंप्रेसिव मैपिंग के लिए यह मौजूद है, और केवल एक। Iterated Function Systems (IFS) इस सिद्धांत का एक उदाहरण हैं।
१.१ परिभाषा
पुनरावृत्त फ़ंक्शंस की प्रणाली फ़ंक्शंस का एक सीमित सेट है: मीट्रिक स्पेस X में X -> X। उनमें से प्रत्येक का विस्तार Fi: H (X) -> H (X) से है, जहाँ H (X) वह स्थान है जहाँ से अंक ग़ैर-रिक्त हैं X के संपीड़ित सबसेट। यदि आप हौसडॉर्फ मीट्रिक का उपयोग करते हैं, तो X पूरा होने पर H (X) पूर्ण है। इसके अलावा, FiX X कंप्रेशन्स H (X) पर भी कंप्रेस रहता है। साथ में, {Fi} निम्नलिखित सूत्र के अनुसार, एक नया संकुचन F: H (X) -> H (X) परिभाषित करते हैं: प्रत्येक A :H (X), F (A) = ∪Fi (A) के लिए। सामान्य सिद्धांत से, एक पूर्ण मीट्रिक स्पेस X के लिए, F में एक निश्चित बिंदु AF: F (AF) = AF है, जिसे किसी भी प्रारंभिक बिंदु से क्रमिक अनुमान द्वारा प्राप्त किया जा सकता है। फिक्स्ड IFS पॉइंट्स को कभी-कभी आकर्षित करने वाले या आक्रमणकारी कहा जाता है।
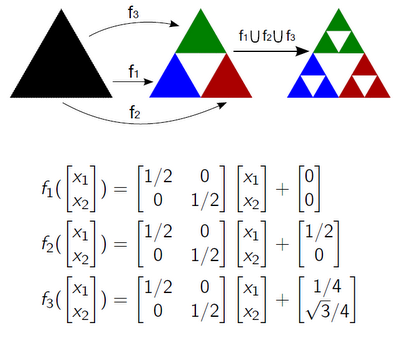
चित्रा 6. IFS का उपयोग कर Sierpinski त्रिकोण के निर्माण का एक उदाहरण।
इस प्रकार, दो कार्य उत्पन्न होते हैं। पहले किसी दिए गए IFS का एक आकर्षित करनेवाला है। दूसरी समस्या पहले के विपरीत है: दिए गए सेट A (H (X) के लिए, IFS {Fi} ढूंढें, जिसके लिए A एक अट्रैक्टर है।
1.2 नियतात्मक एल्गोरिथम
पहली समस्या का निर्धारण एक नियतात्मक एल्गोरिथ्म का उपयोग करके किया जाता है।
हम सेट A0∈H (X) से शुरू करते हैं और क्रमिक रूप से गणना करना शुरू करते हैं
Ak = (Fi (Ak-1) = F (Ak-1), k> 1. श्रृंखला {Ak) k के लिए attractor AF में कनवर्ट करता है।
1.3 रैंडम Iteration एल्गोरिथम
एक वैकल्पिक एल्गोरिदम का गणित - यादृच्छिक पुनरावृत्ति एल्गोरिथ्म, अधिक जटिल है, लेकिन इसका आवेदन सरल है। हम सकारात्मक आवृत्तियों की तुलना मैपिंग फाई से करते हैं। हम एक मनमाना बिंदु x0∈X से शुरू करते हैं। प्रत्येक चरण k + 1 पर, हम सेट {Fi (xk)} से xk + 1 चुनते हैं। Fj (xk) का चयन प्रायिकता pj / pi के साथ किया जाता है। अनुक्रम [5] {xk} एएफ में परिवर्तित होता है। अभ्यास में, कंप्यूटर पर AF सन्निकटन को प्रदर्शित करने के लिए, स्क्रीन पर अनुक्रम बिंदु प्रदर्शित किए जाते हैं। {Pi} नंबर किसी भी तरह से AF को नहीं बदलते हैं, लेकिन इसके सन्निकटन को प्रदर्शित करने की प्रक्रिया को महत्वपूर्ण रूप से प्रभावित करते हैं।
1.4 कोलाज प्रमेय
उलटा समस्या लगभग कोलाज प्रमेय द्वारा हल की गई है। एम। बार्न्सली को उद्धृत करते हुए: "प्रमेय हमें बताता है कि किसी दिए गए सेट के लिए" I समान "के समान IFS को खोजने के लिए, कुछ बड़े सेट के संकुचन मानचित्रण का एक सेट खोजना आवश्यक है, जिसमें इसका सबसेट, मूल सेट, जैसे कि यूनियन, या कोलाज, इस सेट के मैपिंग का सन्निकटन है। मूल सेट होगा। "
1.5 का उपयोग करें
[2]IFS का मुख्य दायरा छवि संपीड़न है। फ्रैक्चर्स के विपरीत मनमानी छवियां आत्म-समान नहीं हैं, इसलिए यह कार्य इतनी आसानी से हल नहीं होता है। यह कैसे करने के लिए 1992 में अर्नोल्ड जैक्विन द्वारा आविष्कार किया गया था, उस समय - स्नातक छात्र माइकल बार्न्सले।
आत्म-समानता आवश्यक है - अन्यथा अपनी क्षमताओं में सीमित होने वाले रूपांतरणों को छवियों को वास्तविकता के करीब लाने में सक्षम नहीं किया जाएगा। और अगर यह भाग और पूरे के बीच नहीं है, तो आप भाग और भाग के बीच खोज कर सकते हैं।
एक सरलीकृत कोडिंग योजना इस प्रकार है:
- छवि को छोटे गैर-अतिव्यापी वर्ग क्षेत्रों में विभाजित किया जाता है जिसे रैंक ब्लॉक कहा जाता है।
- सभी संभावित अतिव्यापी ब्लॉकों का एक पूल बड़े रैंक-ओ - डोमेन ब्लॉकों से चार गुना बनाया जा रहा है।
- प्रत्येक रैंक ब्लॉक के लिए, हम बदले में "डोमेन ब्लॉक" पर प्रयास करते हैं और एक परिवर्तन की तलाश करते हैं जो डोमेन ब्लॉक को वर्तमान रैंक एक के समान बनाता है।
- "रूपांतरण - डोमेन ब्लॉक" जोड़ी, जो आदर्श के पास पहुंच गई, रैंक ब्लॉक के साथ पत्राचार में डाल दी गई है। रूपांतरण गुणांक और डोमेन ब्लॉक के निर्देशांक को एन्कोडेड छवि में संग्रहीत किया जाता है। हमें डोमेन ब्लॉक की सामग्री की आवश्यकता नहीं है - आपको याद है, हम इस बात की परवाह नहीं करते हैं कि किस बिंदु से शुरुआत करें।
तस्वीर में, रैंकिंग ब्लॉक पीले रंग में चिह्नित किया गया है, जो लाल रंग में एक ही डोमेन है। रूपांतरण और परिणाम के चरणों को भी दिखाया गया है।
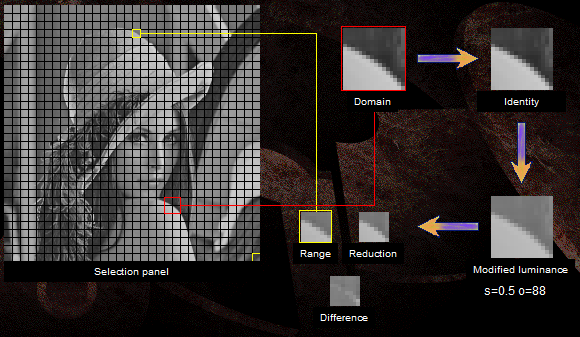
चित्र 7. छवि संपीड़न का एक उदाहरण।
इष्टतम परिवर्तन को प्राप्त करना एक अलग मुद्दा है, लेकिन यह कोई बड़ी बात नहीं है। लेकिन सर्किट का एक और दोष नग्न आंखों को दिखाई देता है। दो मेगापिक्सेल छवि में 32x32 डोमेन ब्लॉक की एक बड़ी संख्या होगी। प्रत्येक रैंक ब्लॉक के लिए उनकी संपूर्ण खोज इस प्रकार की संपीड़न की मुख्य समस्या है - कोडिंग में बहुत लंबा समय लगता है। वे विभिन्न ट्रिक्स का उपयोग करके इससे जूझ रहे हैं, जैसे कि खोज क्षेत्र को कम करना या डोमेन ब्लॉक का प्रारंभिक वर्गीकरण।
डिकोडिंग सरल और काफी त्वरित है। हम किसी भी छवि को लेते हैं, इसे रैंकिंग क्षेत्रों में विभाजित करते हैं, क्रमिक रूप से उन्हें इसी डोमेन क्षेत्र में संबंधित परिवर्तन को लागू करने के परिणाम के साथ प्रतिस्थापित करते हैं (जो भी इस समय इसमें शामिल हैं)। कई पुनरावृत्तियों के बाद, मूल छवि स्वयं की तरह दिखाई देगी:

चित्रा 8. एक संकुचित छवि वसूली का एक उदाहरण।
2. लिंडेनमेयर सिस्टम
[3]पौधों की सुंदरता ने सदियों से गणितज्ञों का ध्यान आकर्षित किया है। पौधों के दिलचस्प ज्यामितीय गुण, जैसे केंद्रीय अक्ष के सापेक्ष पत्ती समरूपता, रेडियल फूल समरूपता और शंकु में बीज की सर्पिल व्यवस्था, सबसे सक्रिय रूप से अध्ययन किया गया। "सौंदर्य समरूपता से संबंधित है" (एच। वीइल। समरूपता)। जीवित जीवों के विकास के दौरान, विशेष रूप से पौधों, नियमित रूप से बहुकोशिकीय संरचनाओं को दोहराते हुए स्पष्ट रूप से देखा जा सकता है। मिश्रित पत्तियों के मामले में, उदाहरण के लिए, छोटे पत्ते जो एक बड़े वयस्क पत्ते का हिस्सा होते हैं, उनका आकार उसी तरह का होता है जैसा कि पूरे पत्ते के गठन के प्रारंभिक चरण में था।
1968 में हंगेरियन जीवविज्ञानी और वनस्पतिशास्त्री अरिस्टिड लिंडेनमेयर ने सरल बहुकोशिकीय जीवों के विकास का अध्ययन करने के लिए एक गणितीय मॉडल का प्रस्ताव रखा, जिसे बाद में विस्तारित किया गया और जटिल शाखाओं वाली संरचनाओं - विभिन्न पेड़ों और फूलों का उपयोग किया गया। इस मॉडल को लिंडेनमायर सिस्टम या केवल एल-सिस्टम कहा जाता है।
२.१ प्रमुख विचार
एल-सिस्टम का मुख्य विचार स्ट्रिंग तत्वों का निरंतर पुनर्लेखन है। यह किस बारे में है? इस मामले में, पुनर्लेखन कुछ नियमों के अनुसार सरल प्रारंभिक वस्तु के कुछ हिस्सों को बदलकर जटिल वस्तुओं को प्राप्त करने का एक तरीका है। एक उत्कृष्ट उदाहरण कोच का सपना है। चित्रा में, सर्जक प्रारंभिक वस्तु है, जिनमें से चेहरे को जनरेटर ऑब्जेक्ट द्वारा बदल दिया जाता है। इसके बाद, नई वस्तु के साथ एक ही काम किया जाता है।

चित्रा 1. कोच हिमपात का एक खंड।
एल-सिस्टम पर लौटना और फ्रैक्टल्स के साथ एक सादृश्य ड्राइंग करना, हम कह सकते हैं कि एल-सिस्टम विशेष नियमों के अनुसार वर्णों की एक स्ट्रिंग के साथ संचालित होता है, जो शुरुआती सरल स्वयंसिद्ध के साथ शुरू होता है। इस प्रकार, एल-सिस्टम एक गणितीय व्याकरण है। लेकिन एल-सिस्टम और औपचारिक व्याकरण के बीच मूलभूत अंतर यह है कि नियम प्रत्येक पंक्ति में एक साथ प्रत्येक वर्ण पर लागू होते हैं, साथ ही टर्मिनल और गैर-टर्मिनल वर्णों की कोई अवधारणा नहीं है। यही है, इस व्याकरण पर "निष्कर्ष" अनिश्चित काल तक चल सकता है।
निम्नलिखित चित्र चॉम्स्की पदानुक्रम में संदर्भ-मुक्त (ओएल), संदर्भ-निर्भर (आईएल) एल-सिस्टम और अन्य औपचारिक व्याकरण के बीच संबंध को दर्शाता है।

चित्रा 2. चॉम्स्की पदानुक्रम।
2.2 सरलतम एल-सिस्टम
साथ ही, चॉम्स्की के वर्गीकरण की तरह, एल-सिस्टम का सरल से जटिल और शक्तिशाली से अपना वर्गीकरण है।
सबसे सरल उदाहरण नियतात्मक संदर्भ-मुक्त एल-सिस्टम, या संक्षेप में डीओएल हैं। मुझे औपचारिक व्याकरण की परिभाषाएँ पसंद नहीं हैं, इसलिए मैं इसे केवल अपने शब्दों में कहूँगा। वर्णों का एक निश्चित समूह है - वर्णमाला। यह वर्णमाला उस रेखा को रिकॉर्ड करती है जिसके साथ एल-सिस्टम काम करता है। एक स्वयंसिद्ध है - एक या एक से अधिक अक्षरों की प्रारंभिक स्ट्रिंग और प्रपत्र के नियमों का एक सेट → एब। एल्गोरिथ्म के प्रत्येक पुनरावृत्ति के दौरान, नियम को वर्तमान लाइन से एक पत्र पर लागू करना, यह (अक्षर) अक्षरों के सेट द्वारा तीर के दाईं ओर प्रतिस्थापित किया जाता है। बहुकोशिकीय जीव अनाबेना कैटेनुला के विकास के एक विशिष्ट उदाहरण पर विचार करना आसान है, जिसे लिंडेनमीयर ने एल-सिस्टम के एक मॉडल का प्रस्ताव करते समय अध्ययन किया था।
हमारी वर्णमाला में निम्नलिखित वर्ण शामिल हैं, जिनमें से प्रत्येक एक निश्चित सेल को नामित करता है: अलार ब्ला ब्र।
Axiom में एक वर्ण होता है:
ω: अर
और चार नियम।
p1: ar → अलब्र
P2: al → blar
p3: br → ar
p4: bl → अल
नियम कहते हैं कि जीव के विकास की प्रक्रिया में कौन से प्रतीक बदलते हैं। चित्र दिखाता है कि, नियमों को लागू करने से, हम कोशिकाओं और विकास के "विभाजन" का पालन करते हैं।

चित्रा 3. एल-प्रणाली अनाबेना कैटेनुला के विकास का अनुकरण करती है।
2.4 लोगो का उपयोग करना
अब तक हमने देखा है कि एक आयामी जीवाणु को कैसे आकर्षित किया जाए, लेकिन प्रसिद्ध बच्चों की प्रोग्रामिंग भाषा लोगो की मदद से, जो एक कछुए को नियंत्रित करने और स्क्रीन पर फाई-गर्स खींचने का प्रस्ताव रखता है, पहले से ही दो-आयामी और तीन-आयामी फ्रैक्टल और दोहराई जाने वाली संरचनाओं को खींचना संभव होगा। कैसे? सब कुछ सरल है। हम वर्णमाला लेते हैं जिसमें प्रत्येक प्रतीक का मतलब दो आयामी या तीन आयामी कछुए के लिए एक कमांड है:
- एफ - आगे बढ़ना और एक रेखा खींचना
- f - बिना कुछ खींचे आगे बढ़ें
- + - बाएँ मुड़ें
- - - ठीक है
- & - ठुकरा दें
- ^ - बारी
- \ - बाईं ओर झुकें
- / - दाईं ओर झुकें
- | - 180 डिग्री के आसपास बारी
ये कमांड दो-आयामी और तीन-आयामी अंतरिक्ष के रोटेशन of, चरण लंबाई और बुनियादी वैक्टर के मानक मूल्यों का उपयोग करते हैं। दो आयामी भग्न और एल-सिस्टम के उदाहरण उन्हें उत्पन्न करते हुए निम्नलिखित चित्र में देखे जा सकते हैं:

चित्रा 4. एल-सिस्टम के उदाहरण।
2.5 पौधे और शाखाओं की संरचना
इससे पहले जो कुछ भी था, सामान्य रूप से, निरंतर घटता है। मॉडलिंग की यह विधि मॉडलिंग पौधों के लिए उनकी शाखीय टोपोलॉजी के साथ उपयुक्त नहीं है। ऐसा करने के लिए, प्रतीकों [और] को अल्फा-विट में जोड़ा गया, जो क्रमशः शाखा की शुरुआत और अंत का संकेत देते हैं। जब कछुआ प्रतीक का सामना करता है [, तो इसकी वर्तमान स्थिति स्टैक पर लिखी जाती है और जब प्रतीक मिलता है तो वहां से पुनर्प्राप्त किया जाता है]। पहले से ही इस तरह के एक सरल व्याकरण पेड़ों के समान काफी दिलचस्प दो आयामी और तीन आयामी वस्तुओं को उत्पन्न कर सकते हैं।

चित्रा 5. ब्रांचिंग एल-सिस्टम के उदाहरण।
2.6 स्टोचस्टिक एल-सिस्टम
स्टोचस्टिक एल-सिस्टम एक नियम के निष्पादन की संभावना को निर्दिष्ट करने की क्षमता को जोड़ते हैं, और सामान्य स्थिति में नियतात्मक नहीं होते हैं, क्योंकि विभिन्न नियमों में बाईं ओर एक ही प्रतीक हो सकता है। यह परिणामी संरचनाओं में यादृच्छिकता के कुछ तत्व का परिचय देता है।
2.7 संदर्भ के प्रति संवेदनशील एल-सिस्टम
औपचारिक व्याकरण में प्रासंगिक निर्भरता की तरह, एल-सिस्टम में नियमों का वाक्य विन्यास जटिल है और प्रतिस्थापित चरित्र के वातावरण को ध्यान में रखता है।
2.8 पैरामीट्रिक एल-सिस्टम
एक चर पैरामीटर (संभवतः एक नहीं) प्रत्येक प्रतीक में जोड़ा जाता है, जो, उदाहरण के लिए, + और - के लिए रोटेशन के कोण के मूल्य को दर्शाता है, चरण लंबाई और रेखा मोटाई, नियम लागू करने के लिए शर्तों की जांच, पुनरावृत्तियों की संख्या की गिनती और "सिग्नल" को आगे और पीछे प्रेषित करता है। । पैरामीट्रिक एल-सिस्टम का एक उदाहरण।
2: बी (2) ए (4, 4)
p1: A (x, y): y <= 3 → A (x x 2, x + y)
P2: A (x, y): y> 3 → B (x) A (x / y, 0)
p3: B (x): x <1 → C
p4: B (x): x> = 1 → B (x - 1)
पैरामीट्रिक संदर्भ-संवेदनशील एल-सिस्टम आपको बहुकोशिकीय जीवों और पौधों के विकास को अनुकरण करने की अनुमति देता है, जैव रासायनिक प्रक्रियाओं और पर्यावरण को ध्यान में रखता है।
2.9 का उपयोग करें
80 के दशक के उत्तरार्ध में, एल-सिस्टम का उपयोग संयंत्र मॉडल की कल्पना करने के लिए किया गया था। अब कंप्यूटर की संभावनाएं बहुत आगे निकल गई हैं। कई गेम और 3 डी मॉडलिंग टूल एल-सिस्टम सहित प्रक्रियात्मक सामग्री निर्माण का उपयोग करते हैं। जैसा कि आप देख सकते हैं, सरल नियमों के एक सेट से आप विभिन्न पौधों की एक बड़ी संख्या प्राप्त कर सकते हैं और उनके साथ पूरे खेत लगा सकते हैं।