नमस्कार, वाचालता!
हबल पर कई दिलचस्प डेटा संरचनाओं का वर्णन है, जैसे कि खंड के पेड़, दुचा, आदि। यदि आप जटिल डेटा संरचनाओं में रुचि रखते हैं, तो बिल्ली में आपका स्वागत है!
अपनी लेख श्रृंखला में, मैं विभिन्न प्रकार के ढेरों को देखूंगा और उन्हें अभ्यास में कैसे लाऊंगा:
1)
द्विपद ढेर2)
बायां ढेर3)
फाइबोनैचि गुच्छा4)
इन डेटा संरचनाओं को अभ्यास में लानासमस्या कथन:एक डेटा संरचना बनाने के लिए जिसमें हमारी बहुत सी वस्तुओं को संग्रहीत किया जाएगा (कार्य के आधार पर अलग-अलग), प्रत्येक ऑब्जेक्ट में एक महत्वपूर्ण फ़ील्ड होगा जिसके द्वारा हम न्यूनतम तत्व को जल्दी से पा सकते हैं। इस संरचना के लिए निम्नलिखित संचालन संभव होने चाहिए:
Make - एक नया खाली ढेर बनाएं,
Insert - ढेर में एक नया तत्व
Insert ,
Minimum - न्यूनतम कुंजी,
ExtractMin - न्यूनतम निष्कर्षण,
Merge - 2 ढेर में विलय,
Decrease - मुख्य कमी,
Delete - किसी वस्तु को हटाना।
कई लोग इस संरचना को लागू करने के सबसे सरल तरीकों से परिचित हैं, जैसे कि एक सरणी :) और एक बाइनरी ढेर। मैं उनकी सादगी और सामान्य ज्ञान के कारण उन पर विस्तार से ध्यान नहीं दूंगा।
जैसा कि आप जानते हैं, एक
बाइनरी हीप के लिए, उपरोक्त संचालन का स्पर्शोन्मुख व्यवहार इस प्रकार है:
Make - O (1)
Merge - O (N)
Insert - ओ (लॉग एन) - जहां एन ढेर में तत्वों की संख्या है।
Minimum - O (1)
ExtractMin - O (लॉग एन)
Decrease - O (लॉग एन)
Delete - O (लॉग एन)
मैं बाइनरी हीप के एल्गोरिथ्म का वर्णन नहीं करूंगा, क्योंकि यह हर जगह बार-बार वर्णित किया गया है, जिसमें हैबे भी शामिल है। उन लोगों के लिए जो बाइनरी हीप से परिचित नहीं हैं, मैं निरंतर पढ़ने से पहले अपने आप को इसके साथ परिचित करने की सलाह दूंगा।
इसके बाद, एक और दिलचस्प डेटा संरचना पर विचार करें जिसे
द्विपद ढेर कहा जाता है।
द्विपद ढेरएक द्विपद ढेर कुछ सीमाओं के साथ
द्विपद पेड़ों का एक सेट है। हम उन्हें थोड़ा बाद में परिचय देंगे।
एक द्विपद वृक्ष एक पेड़ है जिसे पुनरावर्ती रूप से परिभाषित किया गया है:
B
i , B
i - 1 है , जिसमें पेड़ B
i - 1 को जड़ का बायाँ पुत्र बनाया
गया था ।
B
0 केवल शीर्ष है।
बी
0 , बी
2 , बी
3 के उदाहरण:
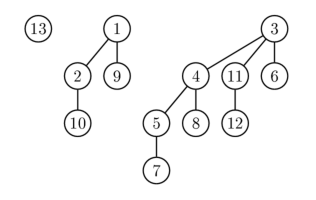
द्विपद वृक्ष (B
k ) में कई रोचक
गुण हैं :
T.1। 2
कश्मीर चोटियों
T.2। पेड़ की ऊँचाई k
T.3। C
i k गहराई के कोने (इसलिए उन्हें द्विपद कहा जाता है: C
i k एक द्विपद गुणांक है)।
T.4। इस क्रम में मूल के बच्चे B, B
k - 2 , ..., B
0 हैं ।
T.5। द्विपद वृक्ष हे (लॉग एन) में अधिकतम शीर्ष ऊंचाई
गुण प्रेरण द्वारा
सिद्ध होते हैं। पेड़ों की बेहतर समझ के लिए मैं पाठकों को स्वयं प्रमाण देने के लिए आमंत्रित करता हूं।
तो, अब वापस
द्विपद हीप में ।
एक द्विपद ढेर द्विपद पेड़ों का एक समूह है, जिसमें निम्नलिखित प्रतिबंध हैं:
1) प्रत्येक द्विपद पेड़ों में, ढेर संपत्ति संरक्षित है।
2) एक ही आकार के दो पेड़ नहीं
3) पेड़ों को आकार के आधार पर ऑर्डर किया जाता है।
आइए बात करते हैं कि कार्यक्रम में द्विपद ढेर कैसे संग्रहीत किया जाएगा। हम "बाएं बेटे - दाएं भाई" विधि का उपयोग करेंगे। हम रूट सूची (
root_list ) को संग्रहीत करेंगे, इसकी लंबाई
root_list.length , जिसमें बढ़ती ऊंचाई के क्रम में द्विपदीय पेड़ों की जड़ें होंगी। प्रत्येक शीर्ष पर निम्नलिखित क्षेत्र होंगे:
data - डेटा जो शीर्ष पर संग्रहीत होता है (जिसके द्वारा हम न्यूनतम पाते हैं)
right - सही भाई
child - बायां बेटा
degree - वर्टेक्स की डिग्री (जाहिरा तौर पर इस क्षेत्र में द्विपद ढेर के पेड़ों का आदेश दिया जाता है)
तुरंत सूचना:संपत्ति H.1:
root_list.length = O (लॉग एन) की लंबाई, जहां N ढेर में तत्वों की संख्या है।
प्रमाण के लिए, यह ध्यान देने के लिए पर्याप्त है कि T.1 के कारण संख्या के बाइनरी अंकन में पेड़ B
k की उपस्थिति है।
आइए उन ऑपरेशनों के विवरण पर चलते हैं जो द्विपद ढेर के साथ किए जा सकते हैं:
मेककार्य : एक खाली ढेर बनाएँ।
एल्गोरिथम : एक खाली
root_list ।
कठिनाई : जाहिर है, चलने का समय ओ (1) है।
मर्जकार्य : 1 में 2 ढेर मिलाएं।
एल्गोरिथ्म : सबसे पहले, 1 रूट सूची में ढेर रूट सूचियों को मिलाएं, डिग्री ऑर्डर को बनाए रखें। एल्गोरिथ्म मर्ज में 2 सरणियों के विलय के समान है:
हम पॉइंटर को सूचियों की शुरुआत में संग्रहीत करते हैं और परिणामी सूची में उनमें से न्यूनतम लिखते हैं, जिसमें से हमने अभी लिखा था उसे अगले में स्थानांतरित कर दिया गया है। इसके बाद, हम नई प्राप्त रूट सूची के अंत से शुरुआत तक जाते हैं और एक ही आकार के पेड़ों को मिलाते हैं। 1. कुछ मामले हो सकते हैं:
1) एक ही आकार के केवल 2 पेड़। फिर उन्हें मिलाएं।
2) एक ही आकार के 3 पेड़। अंतिम 2 को मिलाएं।
दो पेड़ों को मिलाते समय, आपको केवल उस जड़ को देखना होगा, जिसमें से एक में छोटी चाबी हो और दूसरे पेड़ को इस पेड़ की जड़ का बायां बेटा बना दे।
दो ढेर के संयोजन के बाद क्या होता है, इसका एक उदाहरण:
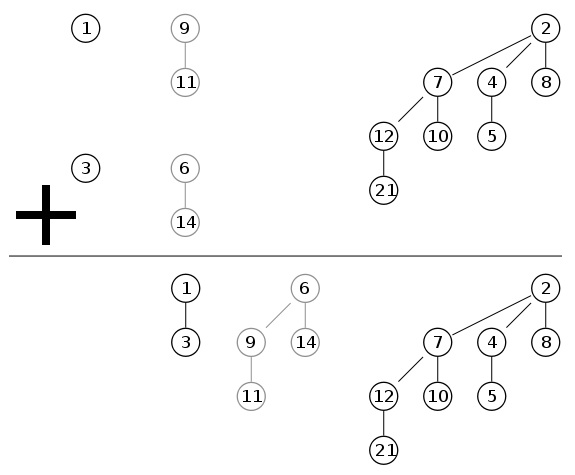जटिलता : ऑपरेटिंग समय O (
root_list1.length ) + O (
root_list2.length ) = (संपत्ति
root_list2.length द्वारा) = O (लॉग एन)।
एक पास (O (लॉग एन)) में हमें संयुक्त द्विपद वृक्ष मिलता है। हमें लगता है कि कुल जटिलता हे (लॉग एन) है।
सम्मिलित करेंकार्य : ढेर में एक नया आइटम डालें।
एल्गोरिथ्म : एक तत्व का एक गुच्छा बनाएं और हमारे गुच्छा के साथ संयोजन करें।
कठिनाई : ओ (1) + ओ (लॉग (एन)) = ओ (लॉग (एन))।
कम से कमकार्य : ढेर पर न्यूनतम खोजें।
एल्गोरिथ्म : जाहिर है, न्यूनतम रूट सूची में है, अर्थात, इसे खोजने के लिए आपको रूट सूची से गुजरना होगा।
कठिनाई : O (
root_list.length ) = O (लॉग (N))।
ExtractMinकार्य : न्यूनतम तत्व को हटा दें।
एल्गोरिथम : इसे
Minimum का उपयोग करके खोजें। इसे रूट लिस्ट से हटा दें। अपने बच्चों की उलटी सूची से, नए ढेर (एच
1 ) के लिए रूट_लिस्ट बनाएं और एच
1 के साथ मूल ढेर को मिलाएं।
कठिनाई : ओ (लॉग एन) के लिए एक न्यूनतम काम निकालने में प्रत्येक ऑपरेशन के बाद से: ओ (लॉग एन) + ओ (लॉग एन) + ओ (लॉग एन) = ओ (लॉग एन)
घटाएँकार्य : इस शीर्ष पर डेटा मान को कम करें।
एल्गोरिथम : शीर्ष पर मान को कम करें। फिर ढेर संपत्ति को संभवतः हमारे शिखर और इसके पूर्वजों के लिए उल्लंघन किया जाएगा, फिर हम उनके स्थानों को बदल देंगे। हम तब तक इस प्रक्रिया को जारी रखते हैं जब तक कि हमारी चोटी "चबूतरे" की जगह पर न हो जाए। एल्गोरिथ्म बाइनरी हीप में एक के समान काम करता है।
कठिनाई : सबसे खराब स्थिति में, हमारा शीर्ष जड़ तक पहुंच जाएगा, अर्थात, हम O (लॉग एन) क्रियाएँ करेंगे (प्रत्येक चरण में शीर्ष बिंदु "एक स्तर ऊपर चबूतरे" और द्विपद वृक्ष की ऊँचाई टी ओ (लॉग एन) है)
हटाएंकार्य : एक मनमाना तत्व निकालें।
एल्गोरिथ्म : सबसे पहले, वर्टेक्स में मूल्य को कम से कम संभव करने के लिए घटाएं का उपयोग करें। और फिर हीप (
ExtractMin ) पर न्यूनतम हटाएं।
कठिनाई : ओ (लॉग एन) + ओ (लॉग एन) = ओ (लॉग एन)
निष्कर्ष।हमने द्विपद ढेर के डेटा संरचना की जांच की और इसके विषम व्यवहार को साबित किया।
अगले लेख में, द्विपद हीप पर आधारित, हम एक और अधिक जटिल डेटा संरचना का निर्माण करेंगे, अर्थात् फिबोनाची ढेर।
आप
बारिश में द्विपद ढेर के साथ खेल सकते हैं
।ifmo.ru /
cat /
view.php /
vis/ heaps/binomial-
2001आप T.Kormen में अधिक विस्तार से पढ़ सकते हैं "एल्गोरिदम: निर्माण और विश्लेषण।"
ध्यान देने के लिए आप सभी का धन्यवाद, और जल्द ही मिलते हैं!