🛸 💤 🍩 हम हिल्बर्ट वक्र का उपयोग करके चित्र बनाते हैं 🍋 🖖🏿 💈

पिछले हफ्ते शनिवार को, "यह शाम थी, कुछ करने के लिए नहीं था," और सॉसर हबरेज़र और मैंने स्पष्ट रूप से बात की कि किस बारे में। और किसी कारण से, हम अपनी अभिव्यक्ति द्वारा किसी फ़ंक्शन के ग्राफ़ के निर्माण के कार्य के उलट समस्या के बारे में बात कर रहे थे। यही है, उदाहरण के लिए, हमारे पास अभिव्यक्ति y ( x ) = (cos ^0.5 x x cos 200 x + | | ^0.5 - 0.7) (4 - x ² ) ^{0.01 है} । इस तरह के समारोह का ग्राफ कुछ हद तक दिल की याद दिलाता है।

लेकिन हम विपरीत सवाल में रुचि रखते थे, कैसे, उदाहरण के लिए, दिल की एक छवि होने, एक फ़ंक्शन के लिए एक अभिव्यक्ति कैसे प्राप्त करें जिसका ग्राफ खुद यह दिल होगा।

मैं किसी फूरियर श्रृंखला को याद नहीं करना चाहता था, लेकिन मैं कुछ सरल और सुंदर चाहता था। हम इस मुद्दे के बारे में जानने वाले परिणामों को याद करने लगे। परिणाम एक ऐसा कार्यक्रम था जो छवि में एक टूटी हुई रेखा उत्पन्न करता है, कुछ हद तक मूल छवि की याद दिलाता है। वूफ़ नामक बिल्ली के बच्चे के उदाहरण का उपयोग करते हुए, यह कुछ इस तरह दिखता है (दूर से बेहतर दिखना):

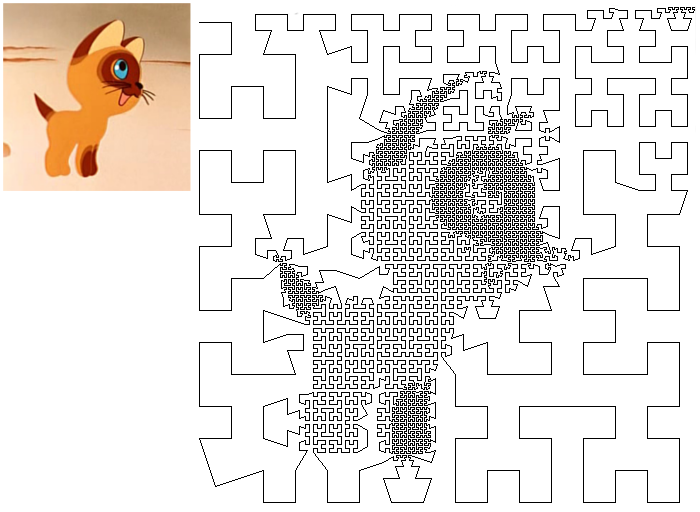
यदि आप इसे करने के तरीके में रुचि रखते हैं, साथ ही साथ हेम्प फॉर्मूला के बारे में भी सीखते हैं, तो एक ऐसा फॉर्मूला जिसका ग्राफ एक ही फॉर्मूला है, तो हैबरकट पर आपका स्वागत है। (कई तस्वीरें होंगी)

तो, चलिए कुछ परिणामों को याद करते हैं।

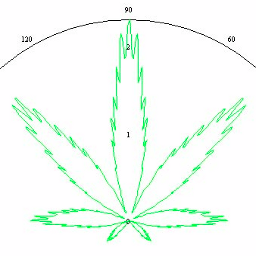
भांग का सूत्र । 2005 के आसपास, भांग सूत्र सक्रिय रूप से विकसित और चर्चा की गई थी । फार्म के ध्रुवीय निर्देशांक में सरल सूत्र

R ( t ) = (1 + sin t ) (1 + 0.9 t cos 8 t ) (1 + 0.1, cos 24 t ),
R ( t ) = (1 + sin t ) (1 - 0.9 sin | sin 4t |) ⋅ (0.9 + 0.05 0.0 cos 200 t ),
R ( t ) = (1 + sin t ) (1 + 0.9 t cos 8 t ) (1 + 0.1 (cos 24 t ) (0.5 + 0.05 140 cos 140 t )

बेशक उनके पास अच्छे ग्राफिक्स हैं, लेकिन यह सब एंटोन सुखिनोव के परिणाम की तुलना में कुछ भी नहीं है।

एंटोन सुखिनोव ने क्या किया? तरबूज मंच पर 2005 में उन्होंने निम्नलिखित जटिल सूत्र का प्रस्ताव किया (यदि टाइप करते समय मुझसे गलती नहीं हुई):

फिर, केवल उन बिंदुओं को आरेखित करें जिसके लिए F ( a , r )> 0 और फ़ंक्शन के मान के आधार पर एक रंग का चयन करते हुए, हम निम्नलिखित छवि प्राप्त करते हैं:

पागल हो, है ना?

टॅपर फार्मूला । असमानता पर विचार करें

, और नंबर k हो
48584506361897134235820959624942020445814005879832445494830930850619347
04708809928450644769865524364849997247024915119110411605739177407856919
75432657185544205721044573588368182982375413963433822519945219165128434
83329051311931999535024137587652392648746133949068701305622958132194811
13685339535565290850023875092856892694555974281546386510730049106723058
93358605254409666435126534936364395712556569593681518433485760526694016
12512669514215505395545191537854575257565907405401579290017659679654800
64427829131488548259914721248506352686630476300।

यह पता चला है कि इस असमानता को संतुष्ट करने वाले बिंदुओं ( x , y - k ) का सेट और इस तरह 0 and x ≤ 106 और k ≤ y + k + 17 इस प्रकार है:

और यह असमानता ही है। यह स्पष्ट है कि बेशक, छवि बस के बीच एन्क्रिप्टेड है, लेकिन फिर भी परिणाम बहुत सुंदर है और यह स्पष्ट नहीं है कि इस तरह का आविष्कार कैसे किया जा सकता था।
अधिक विवरण विकिपीडिया पर पाया जा सकता है: ट्यूपर का आत्म-संदर्भ सूत्र , और हम विशेष परिणामों से बड़े पैमाने पर तरीकों पर आगे बढ़ेंगे।

चलने योग्य कार्यों की प्रणाली। संभवतः हर कोई जिसके पास कम से कम फ्रैक्टल्स के साथ थोड़ा सा अनुभव है, वह जानता है कि चलने योग्य कार्यों की प्रणाली क्या है। CIF दर्जनों पत्तियों के जोड़े का उपयोग करके वास्तविक पत्तियों, पेड़ों, शाखाओं के समान चित्र प्राप्त करने की अनुमति देता है:

विचार है कि आप उलटा समस्या को हल करने की कोशिश कर सकते हैं - एक दी गई छवि से सीआईएफ का वर्णन करने वाली संख्याओं का एक सेट प्राप्त करने के लिए, माइकल बार्न्सले को भग्न संपीड़न के साथ आने की अनुमति दी। भग्न संपीड़न के बारे में बात करने का कुछ प्रयास पहले से ही एक हब पर किया गया है: भग्न छवि संपीड़न के मूल । लेकिन जो लोग विस्तार से समझना चाहते हैं, उनके लिए मैं एस। वेलस्टीड की पुस्तक "फर्स्टल्स एंड वेवलेट्स फॉर कम्प्रेसिंग इमेजेज इन एक्शन" की पहली छमाही की सिफारिश करूंगा।

भग्न रेखाएँ । वास्तव में, फ्रैक्टल कम्प्रेशन अल्गोरिद्म इसमें उपयोग करने योग्य कार्यों की प्रणालियों का उपयोग नहीं करता है, लेकिन आंशिक चलने योग्य कार्यों की तथाकथित प्रणाली। फिर भी, छवियों का एक वर्ग है, जिसके लिए सीआईएफ के साथ आना आसान है, जिसके आकर्षण वे हैं। ऐसी छवियां भग्न रेखाएं हैं। एक भग्न रेखा एक शब्द है, जिसके प्रत्येक अक्षर में दिए गए शब्द की कम प्रतियां शामिल हैं, और इसी तरह। "HABR" शब्द के उदाहरण पर यह कुछ इस तरह दिखता है:

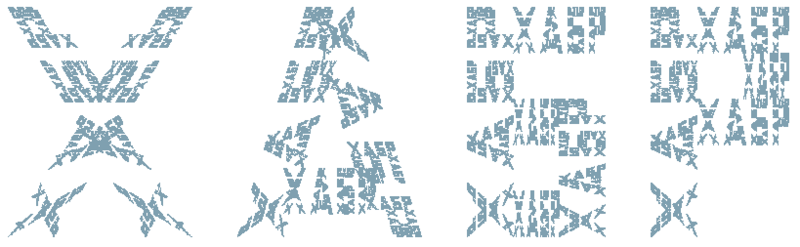
यह समझना आसान है कि एक मनमाने शब्द के लिए यह कैसे करना है, प्रत्येक शब्द को समांतर चतुर्भुज के रूप में प्रस्तुत करने के लिए थोड़ा समय बिताने के लिए पर्याप्त है। कम से कम पांच साल पहले ऐसा किया गया था। एक विस्तृत विवरण और कोड लेख फ्रैक्टल पंक्तियों में पाया जा सकता है।

वी। जे। Møller। फ्रैक्टल्स, कैओस, पावर लॉज़ पुस्तक के माध्यम से पत्ता। अनंत स्वर्ग "एम। श्रोएडर से लघुचित्र, आप निम्नलिखित चित्र पर ठोकर खा सकते हैं:

यह बहुत अच्छा लग रहा है, और यह स्पष्ट है कि यह एक मनमाना छवि के साथ किया जा सकता है। पुस्तक यह नहीं बताती है कि इसे कैसे चित्रित किया गया था, लेकिन अपने लिए अनुमान लगाना मुश्किल नहीं है।

सबसे पहले आपको हिल्बर्ट वक्र के निर्माण के लिए एल्गोरिथ्म लेने की आवश्यकता है। लेकिन किसी एल-सिस्टम की मदद से नहीं, बल्कि एक ईमानदार पुनरावर्ती एल्गोरिदम। और फिर हम इसे निम्नानुसार संशोधित करते हैं। यदि वर्ग की चमक निर्दिष्ट दहलीज से अधिक है और इसके चार उप-वर्गों में वक्र खींचना आवश्यक नहीं है, तो हम मानते हैं कि वर्ग में ही वक्र खींचना आवश्यक नहीं है। हालांकि नीचे दिए गए कोड से इसे समझना शायद आसान है।

Point2D[] drawHilbertCurve(Point2D p, double size, int d) { Point2D q = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2), p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2)); if (size <= 2) { if (blockIsWhite(p, q)) { return null; } else { Point2D cc = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 2, p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 2); return new Point2D[]{cc, cc}; } } else { Point2D cl = new Point2D.Double( p.getX() + size * cos(PI * (d + 1) / 2) / 2, p.getY() + size * sin(PI * (d + 1) / 2) / 2); Point2D cc = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 2, p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 2); Point2D br = new Point2D.Double( p.getX() + size * cos(PI * d / 2), p.getY() + size * sin(PI * d / 2)); Point2D[] p1 = drawHilbertCurve(cl, size / 2, d - 1); Point2D[] p2 = drawHilbertCurve(cl, size / 2, d); Point2D[] p3 = drawHilbertCurve(cc, size / 2, d); Point2D[] p4 = drawHilbertCurve(br, size / 2, d + 1); if (p1 == null && p2 == null && p3 == null && p4 == null && blockIsWhite(p, q)) { return null; } else { if (p1 == null) { p1 = new Point2D[2]; p1[0] = p1[1] = new Point2D.Double( cl.getX() + size * sqrt(2) * cos(PI * (d - 0.5) / 2) / 4, cl.getY() + size * sqrt(2) * sin(PI * (d - 0.5) / 2) / 4); } if (p2 == null) { p2 = new Point2D[2]; p2[0] = p2[1] = new Point2D.Double( cl.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 4, cl.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 4); } if (p3 == null) { p3 = new Point2D[2]; p3[0] = p3[1] = new Point2D.Double( cc.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 4, cc.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 4); } if (p4 == null) { p4 = new Point2D[2]; p4[0] = p4[1] = new Point2D.Double( br.getX() + size * sqrt(2) * cos(PI * (d + 1.5) / 2) / 4, br.getY() + size * sqrt(2) * sin(PI * (d + 1.5) / 2) / 4); } drawLine(p1[0], p2[0]); drawLine(p2[1], p3[0]); drawLine(p3[1], p4[1]); } return new Point2D[]{p1[1], p4[0]}; } }

 boolean blockIsWhite(Point2D p, Point2D q) { int l = (int) min(p.getX(), q.getX()); int r = (int) max(p.getX(), q.getX()); int t = (int) min(p.getY(), q.getY()); int b = (int) max(p.getY(), q.getY()); double c = 0; for (int i = l; i < r; ++i) { for (int j = t; j < b; ++j) { c += (srcImage.getRGB(i, j) & 0x0000FF) / 255.0; } } return c / ((b - t) * (r - l)) > threshold * (1 - log(2) / log(b - t)); }

छवि को कार्यक्रम में खिलाए जाने से पहले, इसे ग्रे के रंगों में अनुवाद किया गया था और प्रयोगात्मक रूप से चमक और इसके विपरीत समायोजित किया गया था। उदाहरण के लिए, कार्यक्रम के टक्स पर सेट होने पर यहां क्या हुआ:

कार्यक्रम का स्रोत कोड ।

यदि कोई चर्चा किए गए क्षेत्र से कुछ अन्य सुंदर परिणामों को जानता है, तो कृपया टिप्पणियों में इस बारे में लिखें।

हम हिल्बर्ट वक्र का उपयोग करके चित्र बनाते हैं

More articles: