🙇🏼 👐🏽 🏡 दो आयामी पैकेजिंग के बारे में: ऑफ़लाइन एल्गोरिदम 🌁 💇🏼 ⏏️

आज, प्रिय हेबर, मैं आपको कॉम्बीनेटरियल अनुकूलन के बारे में एक कहानी बताऊंगा।
प्राचीन काल से (कम से कम पिछली शताब्दी की शुरुआत से), गणितज्ञों ने सोचा कि कैसे एक बैकपैक में आवश्यक और उपयोगी वस्तुओं की एक निश्चित मात्रा में ~~बीयर~~ को बेहतर तरीके से ~~रखा~~ जाए। थप्पड़ और उसके उपप्रकार की समस्या तैयार की गई थी - उनमें से हजारों! - जिसमें रुचि रखते हैं कंप्यूटर वैज्ञानिक, क्रिप्टोग्राफर और यहां तक कि भाषाविद भी।

कंटेनरों में पैकिंग का कार्य ( बिन पैकिंग समस्या ), जिनमें से एक किस्में दो-आयामी पैकेजिंग (2-आयामी बिन पैकिंग) की समस्या है, जो नैकपैक समस्या से जुड़ी है। कई विविधताओं को फिर से त्यागने के बाद, हम अंत में एक अर्ध-सीमित पट्टी (2-आयामी स्ट्रिप पैकिंग, 2DSP) में दो आयामी पैकिंग के लिए आते हैं। महसूस करें कि पर्दे के पीछे पहले से कितना दिलचस्प है? लेकिन हमने वर्गीकरण के माध्यम से वैडिंग समाप्त नहीं की है। 2DSP में दो इनपुट विकल्प होते हैं: जब पैक वस्तुओं का सेट अग्रिम (ऑफलाइन समस्या) में जाना जाता है और जब डेटा बैचों (ऑनलाइन समस्या) में आता है।

यह आलेख ऑफ़लाइन-वैरिएंट 2DSP को हल करने के लिए एल्गोरिदम पर चर्चा करता है। कट के नीचे, रंगीन वर्गों के साथ थोड़ा सा मैटरियल और बहुत सारे चित्र हैं।

वास्तव में, समस्या क्या है?

द्वि-आयामी पैकिंग समस्या के एक विशेष मामले के रूप में, 2DSP में एक विशेष आकार की वस्तुओं को एक विशेष आकार के कंटेनरों की परिमित संख्या में इस तरह से पैक किया जाता है कि उपयोग किए जाने वाले कंटेनरों की संख्या सबसे छोटी या वस्तुओं की संख्या या मात्रा (पैक) सबसे बड़ी होती है। दो-आयामी पैकेजिंग के साथ अंतर यह है कि केवल एक कंटेनर है, और कंटेनरों की संख्या को कम करने के बजाय, हम एक की ऊंचाई को कम करते हैं। यदि आप चाहते हैं तो हम अधिकतम पैकिंग घनत्व प्रदान करते हैं।

चूंकि समस्या एनपी-हार्ड है, अनुसंधान मुख्य रूप से अनुमानित समाधान एल्गोरिदम विकसित करने पर केंद्रित है। ( आनुवंशिक एल्गोरिथ्म Habré पर उल्लेख किया गया था)। अनुमानित एल्गोरिदम एक निश्चित सटीकता के साथ इष्टतम समाधान ढूंढते हैं, लेकिन किसी भी डेटा सेट के लिए इष्टतम पैकेजिंग की गारंटी नहीं देते हैं। इस मामले में, इष्टतमता की कसौटी इस पर निर्भर करती है कि आपने क्या अनुकूलन करने की कोशिश की थी।
मैं सबसे सरल रणनीतियों के बारे में बात करूंगा और यह सब जीवन में लागू होता है (बीयर के साथ एक बैकपैक को छोड़कर)।

तो, हमारे पास एक निश्चित चौड़ाई W और अनंत ऊंचाई के साथ n आयतों का एक सेट और एक अर्ध-सीमित कंटेनर-ग्लास है। चौड़ाई में प्रत्येक आयत डब्ल्यू से अधिक नहीं है। कार्य आयतों को ओवरले और चौराहों के बिना ग्लास में डालना है ताकि ग्लास जितना संभव हो उतना छोटा हो जाए। मान लेते हैं कि सभी आयतों को ऑर्थोगोनली पैक किया जाना चाहिए, उन्हें घुमाया नहीं जा सकता।


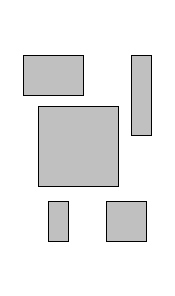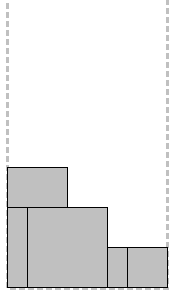स्रोत डेटा (XX सदी की शुरुआत, घनवाद)	अर्ध-सीमित लेन	पैकेजिंग विकल्प (बदतर)	पैकेजिंग विकल्प (बेहतर)

यह देखा जा सकता है कि समस्या का एक आदर्श समाधान है जिसमें पैक्ड आयतों की ऊंचाई पट्टी की चौड़ाई से विभाजित उनके कुल क्षेत्रफल के बराबर है।

चिड़ियाघर एल्गोरिदम

2DSP के ऑफ़लाइन संस्करण के लिए, सभी पैक किए गए आयतों का आकार तुरंत ज्ञात है, इसलिए उन्हें एक विशिष्ट मानदंड के अनुसार चुना जा सकता है, समूहीकृत या उपयुक्त स्थानों में टकराया जा सकता है। अधिकांश एल्गोरिदम इस पर आधारित हैं:

स्तर (स्तर)
शेल्फ (शेल्फ)
समतल (समतल)

फ्लैट एल्गोरिदम आयतों को सख्ती से एक दूसरे के करीब रखते हैं, लेकिन यह सबसे सफल रणनीति नहीं है, क्योंकि यह पहली नज़र में लग सकता है। स्तर वाले पट्टी को चयनित आयतों में से एक के बराबर ऊंचाई के स्तर में विभाजित करते हैं, और एक निश्चित मानदंड के अनुसार सभी अन्य को विशिष्ट स्तर पर रखते हैं। शेल्फ एक साथ कई अलमारियों (अलमारियों) को पूर्व निर्धारित करती है, और उनके साथ आयतों को धक्का देती है, यह व्यवहार ऑनलाइन-एल्गोरिदम के लिए विशिष्ट है, और यह पूरी तरह से अलग कहानी है।

सामान्य शब्दों का विस्तार करने के लिए, यह क्रम में सब कुछ के बारे में बेहतर है।

अगला फिट घटाना

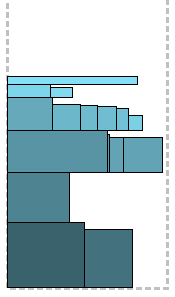
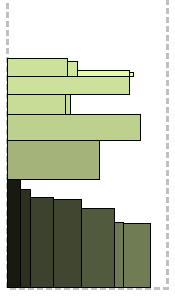
एल्गोरिथ्म, जैसा कि वे कहते हैं, "माथे में।" आयताकार गैर-बढ़ती ऊंचाई (घटते उच्च संकेत) द्वारा क्रमबद्ध होते हैं, उच्चतम पट्टी के निचले बाएं कोने में स्थित होता है, जिससे ऊंचाई में पहले स्तर के बराबर स्तर शुरू होता है। शेष आयताकार बाएं से दाएं स्थित हैं, जबकि वर्तमान स्तर पर जगह है। एक आयत जो एक स्तर पर फिट नहीं होती है उसे अगले स्तर पर बनाने के लिए शीर्ष पर रखा जाता है, और इसी तरह।
प्रत्येक एल्गोरिथ्म के लिए चित्र निम्न दो उदाहरणों के लिए बनाए जाएंगे: स्पष्टता के लिए, बाएं में, आयतों का आकार लम्बी हो जाता है, दाएं में - अधिक चौकोर।

NFDH एल्गोरिथम

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम 
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: स्तर = 0;  h (स्तर) = 0;  w (स्तर) = 0;  मैं = १
  2: गैर-बढ़ती ऊंचाई के क्रम में आयतों को क्रमबद्ध करें जैसे कि h (L1) (h (L2) (... ≥ h (Ln)
  3: पैक आयत ली बाईं पट्टी के तल पर औचित्य
  4: एच (स्तर) = एच (ली);  w (स्तर) = w (Li)
  5: i = 2. के लिए
  6: यदि डब्ल्यू - डब्ल्यू (स्तर) if डब्ल्यू (ली) तब
  7: आयत Li-1 के दाईं ओर आयत Li पैक कीजिए
  8: w (स्तर) + = w (Li)
  9: और [डब्ल्यू - डब्ल्यू (स्तर) <w (ली)]
 10: पिछले एक से ऊपर एक नया स्तर बनाएं और आयत ली को नए स्तर पर पैक करें
 11: स्तर ++;  w (स्तर) = w (Li);  एच (स्तर) = एच (स्तर -1) + एच (ली)
 12: अंत यदि
 13: के लिए अंत
 14: प्रिंट H = h (स्तर)

पहले फिट घटते-बढ़ते

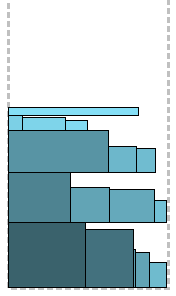
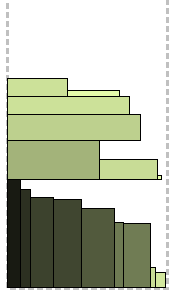
पिछले एल्गोरिथम के समान, इस अंतर के साथ कि प्रत्येक अगली आयत के लिए न केवल अंतिम स्तर पर खोज की जाती है, बल्कि सबसे कम से शुरू होती है। इसलिए "पहले फिट" - आयत को नीचे से पहले उपयुक्त स्तर पर रखा गया है। सहज रूप से, पैकेजिंग बेहतर होगी। एक और महत्वपूर्ण अंतर प्रदर्शन में है, क्योंकि सबसे खराब स्थिति में, आपको हर स्तर पर नीचे से सभी स्तरों पर विचार करना होगा।

एफएफडीएच एल्गोरिथम

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: स्तर = 0;  h (स्तर) = 0;  i = 1;  LevelNum = 1
  2: गैर-बढ़ती ऊंचाई के क्रम में आयतों को क्रमबद्ध करें जैसे कि h (L1) (h (L2) (... ≥ h (Ln)
  3: पैक आयत ली बाईं-पट्टी के निचले हिस्से में बांधा हुआ;  एच (स्तर + 1) = एच (ली)
  4: i = 2. के लिए
  5: पर्याप्त स्थान के साथ निम्नतम के लिए सभी स्तरों (नीचे से) खोजें
  6: यदि ऐसा स्तर मौजूद है तो
  7: पैक आयत ली उस स्तर पर उचित है
  8: और [सभी मौजूदा स्तरों में अपर्याप्त जगह है]
  9: LevelNum ++;  स्तर = LevelNum;  एच (स्तर) = एच (स्तर -1) + एच (ली)
 10: नए स्तर पर आयत ली पैक करें
 11: अंत यदि
 12: के लिए अंत
 13: प्रिंट H = h (स्तर)

सबसे अच्छा फिट कम हो रही है

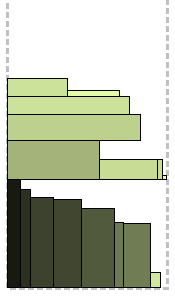
पिछले एल्गोरिथ्म का संशोधन। इसका सार अगले आयत को पैक करने के लिए उपयुक्त स्तरों का है, न कि पहला, लेकिन सबसे अच्छा चुना जाता है। सबसे अच्छा स्तर वह है जहां वर्तमान आयत को पैक करने के बाद न्यूनतम स्थान होगा। सीधे शब्दों में कहें तो न्यूनतम उपयुक्त स्थान को चुना जाता है, जो स्तरों को बेहतर तरीके से भरने में योगदान देता है।

बीएफडीएच एल्गोरिथम

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: स्तर = 0;  h (स्तर) = 0;  i = 1;  LevelNum = 1
  2: गैर-बढ़ती ऊंचाई के क्रम में आयतों को क्रमबद्ध करें जैसे कि h (L1) (h (L2) (... ≥ h (Ln)
  3: पैक आयत ली बाईं-पट्टी के निचले हिस्से में बांधा हुआ;  एच (स्तर + 1) = एच (ली)
  4: i = 2. के लिए
  5: पर्याप्त स्थान के साथ स्तर के लिए सभी स्तरों की खोज करें और न्यूनतम अवशिष्ट स्थान है
  6: यदि ऐसा स्तर मौजूद है तो
  7: पैक आयत ली उस स्तर पर उचित है
  8: और [सभी मौजूदा स्तरों में अपर्याप्त जगह है]
  9: शीर्ष-स्तर के ऊपर एक नया स्तर बनाएं और आयत ली को पैक करें
 10: LevelNum ++;  स्तर = LevelNum;  एच (स्तर) = एच (स्तर -1) + एच (ली)
 11: अंत यदि
 12: के लिए अंत
 13: प्रिंट H = h (स्तर)

नैकपैक 0-1

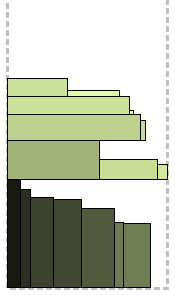
यह अधिक विस्तार से रहने के लायक है। नैकपैक 0-1 नैकपैक समस्या का एक विशेष मामला है; यह उल्लेखनीय है कि मुख्य प्रश्न का उत्तर देने के अलावा (नहीं, 42 नहीं, लेकिन परिणामस्वरूप पैकेजिंग की मात्रा) यह एक समाधान भी देता है - उन वस्तुओं की एक सूची जो पैक किए जाने की आवश्यकता है। प्रक्रिया निम्नानुसार है: आयताकार गैर-बढ़ती ऊंचाई द्वारा क्रमबद्ध हैं; पहला आयत एक नए स्तर पर पैक किया गया है; इस स्तर के लिए नैकपैक 0-1 समस्या का एक समाधान है, जो हमें क्षेत्र में अधिकतम आयतों की एक सूची देता है। चयनित आयतों को अनपैक्ड सूची से पैक और निकाला जाता है, स्तर बंद होता है और एक नया खुलता है - प्रारंभिक रूप से, शेष के पहले (उच्चतम)। जब तक आयतें न हों तब तक दोहराएं।

एल्गोरिथ्म KP01

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: गैर-बढ़ती ऊंचाई के क्रम में आयतों को क्रमबद्ध करें जैसे कि h (L1) (h (L2) (... ≥ h (Ln)
  2: स्तर = 0
  3: जबकि वहाँ अनपैक आयतें हैं
  4: पैक पहले अनपैक आयत, ली कहते हैं
  5: एच (स्तर) + = एच (ली)
  6: KP01 उदाहरण को हल करें
  7: चयनित आयतों को पैक करें
  8: स्तर = स्तर + 1
  9: जबकि अंत
 10: प्रिंट H = h (स्तर)

विभाजन फिट है

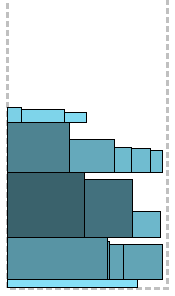
एल्गोरिथ्म को "फूट डालो और जीतो" के सिद्धांत पर FFDN में सुधार करने के लिए डिज़ाइन किया गया है। शुरुआत के लिए, आयताकार जो आधे से अधिक चौड़ी हैं पट्टी का चयन किया जाता है। उन्हें पहले पैक किया जाएगा। इनमें से, यहां तक कि व्यापक लोगों को चुना जाता है - पट्टी के 2/3 से अधिक; वे एफएफडीएच एल्गोरिथ्म के साथ पैक किए गए हैं। उनके ऊपर, अगले स्तर से शुरू करते हैं (चलो इसे स्तर आर कहते हैं), शेष लोगों को पैक किया जाता है, जो अभी भी 1/2 से अधिक व्यापक हैं, लेकिन पहले से ही 2/3। उन्हें एफएफडीएच का उपयोग करके भी पैक किया जाता है। यह पृथक्करण केवल पैक किए गए आर के स्तर पर 1/3 की चौड़ाई के साथ एक मुक्त क्षेत्र बनाता है, आर के स्तर पर शुरू होता है और पैकेज की वर्तमान शीर्ष सीमा के साथ समाप्त होता है (अर्थात, यह आयतों के ऊपर 1/2 <चौड़ाई <= 2/3) का विस्तार नहीं करता है। सभी शेष आयतें, जो 1/2 पट्टियों की तुलना में संकरी हैं, समान FFDH का उपयोग करके सभी को पहले निर्मित क्षेत्र में पैक किया जाता है, और यदि वे फिट नहीं होते हैं, तो ऊपर से। यह शब्दों में बोझिल लगता है, चित्र स्पष्ट होना चाहिए। और उन लोगों के लिए जो पहले से ही मेरे साहित्यिक अभ्यास से थक चुके हैं - एक छद्मकोश:

एसएफ एल्गोरिथ्म

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
 1: चलो m: 1 सबसे बड़ा पूर्णांक है जिसके लिए L में सभी आयतें हैं
    चौड़ाई अधिकतम 1 = मी
 2: आयतों L की सूची को दो उपविभागों L1 और L2 में विभाजित करें
    ऐसा है कि L1 चौड़ाई की आयतों की एक सूची से अधिक है
    1 / (m + 1), जबकि L2 सबसे अधिक 1 / (m + 1) चौड़ाई की आयतों की एक सूची है
 3: FFDH एल्गोरिथ्म का उपयोग करते हुए L1 आयतों को पट्टी में पैक करें
 4: इस पैकिंग के ब्लॉक को फिर से व्यवस्थित करें, जैसे कि चौड़ाई के
    चौड़ाई से अधिक (m + 1) / (m + 2) नीचे हैं
    सबसे अधिक (m + 1) / (m + 2)
 5: क्षेत्र आर में अधिकतम 1 / (m + 2) पर चौड़ाई के आयताकार पैक करें
    FFDH एल्गोरिथ्म का उपयोग करना, जैसे कि कोई आयत शीर्ष को ओवरलैप नहीं करता है
    R और R में फिट होने में विफल रहने वालों को L1 की पैकिंग के ऊपर पैक किया जाता है
 6: प्रत्येक स्तर की ऊंचाई जोड़कर, पट्टी की ऊंचाई का उत्पादन

शामिल हों

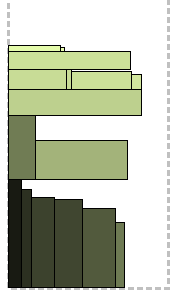
जाहिर है, यह एल्गोरिथ्म इनपुट डेटा की एक निश्चित प्रकृति के लिए कैद था, ठीक है, किसी भी व्यावहारिक स्थिति को अस्तित्व का अधिकार है। अब आप खुद ही सब कुछ समझ जाएंगे। आयताकार क्रमबद्ध, हमेशा की तरह, गैर-बढ़ती ऊंचाइयों द्वारा जोड़े में जोड़ दिए जाते हैं ताकि जोड़ी में ऊंचाई का अंतर किसी दिए गए अंश से अधिक न हो, आमतौर पर 0-10%। एक और शर्त यह है कि उनकी कुल चौड़ाई पट्टी में फिट होती है। परिणामस्वरूप "सुपर-आयताकार" NFDH और FFDH का उपयोग करके एक जोड़ी के बिना शेष के साथ मिलकर पैक किया जाता है, सबसे अच्छा समाधान चुना जाता है।
इस एल्गोरिथ्म की एक भिन्नता है जब आयतों को चौड़ाई द्वारा क्रमबद्ध किया जाता है और लंबवत रूप से संयोजित किया जाता है, एक ही संख्या में प्रतिशत में चौड़ाई की अधिकतम विचलन के लिए एक ही स्थिति के साथ।

एल्गोरिथ्म में शामिल हों

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  एच (ली)}, एक के रूप में निरंतर गामा
        प्रतिशत और स्ट्रिप चौड़ाई W
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: गैर-बढ़ती ऊंचाई के क्रम में आयतों को क्रमबद्ध करें जैसे कि h (L1) (h (L2) (... ≥ h (Ln)
  2: j = 1
  3: जबकि j + 1 do n करते हैं
  4: if (h (Lj) - h (Lj + 1)) / h (Lj) * 100 <गामा
          और w (Lj) + w (Lj + 1) L W तब
  5: w (Lj) + = w (Lj + 1)
  6: j + = 2
  7: और
  8: j ++
  9: अंत अगर
 10: जबकि अंत
 11: आयतों को पैक करने के लिए NFDH और FFDH एल्गोरिदम निष्पादित करें
 12: सबसे अच्छा समाधान से, मूल उदाहरण की एक संभव पैकिंग का निर्माण करें
 13: प्रत्येक स्तर की ऊंचाई जोड़कर, पट्टी की ऊंचाई का उत्पादन

फ्लोर सीलिंग नो रोटेशन

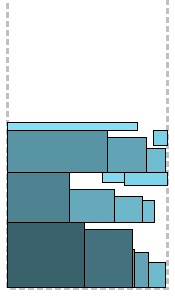
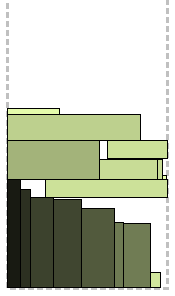
यदि आप अभी भी अंतरिक्ष स्तरों पर शेष के बारे में चिंतित हैं, तो यह एल्गोरिथ्म आपके लिए है। रेक्टैंगल्स को गैर-बढ़ती ऊंचाइयों (अप्रत्याशित रूप से, हाँ?) द्वारा सॉर्ट किया जाता है और कुछ संशोधनों के साथ बीएफडीएच एल्गोरिथ्म लागू किया जाता है। प्रत्येक स्तर पर एक "मंजिल" और एक "छत" है। जब तक संभव हो, आयताकार "मंजिल" पर बाईं से दाईं ओर पैक किया जाता है। जब जगह समाप्त होती है, तो दाएं से बाएं ओर "छत" पर पैक करने का प्रयास किया जाता है; यदि छत पर जगह नहीं है, तो केवल एक नया स्तर शुरू होता है। बीएफडीएच की सर्वश्रेष्ठ परंपराओं में, हर कदम पर सभी स्तरों को देखा जाता है - सबसे पहले "मंजिल", फिर "छत" - सबसे उपयुक्त जगह के लिए। पैकेजिंग, जैसा कि आप देखते हैं, खराब नहीं है। विधि सफलतापूर्वक "छत" पर सबसे छोटी आयतों को पैक करती है।

FCNR एल्गोरिथम

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: गैर-बढ़ती ऊंचाई के क्रम में आयतों को क्रमबद्ध करें जैसे कि h (L1) (h (L2) (... ≥ h (Ln)
  2: i = 1. के लिए
  3: अगर ली सीलिंग संभव है
  4: न्यूनतम अवशिष्ट स्थान के साथ छत पर ली पैक करें
  5: और [ली छत संभव नहीं है]
  6: अगर ली मंजिल संभव है
  7: न्यूनतम अवशिष्ट स्थान के साथ फर्श पर ली पैक करें
  8: और [ली मंजिल संभव नहीं है]
  9: स्तर ++;
 10: अंत यदि
 11: अंत यदि
 12: के लिए अंत
 13: प्रत्येक स्तर की ऊंचाई जोड़कर, पट्टी की ऊंचाई एच का उत्पादन

Sleator

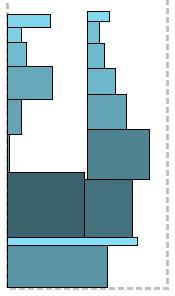
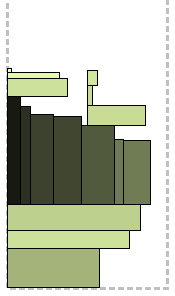
स्तरों में विभाजित किए बिना, "फ्लैट" एल्गोरिदम का समय आ गया है। स्लेटोर एल्गोरिथ्म एक बैकपैक को पैक करने के सहज सिद्धांत का उपयोग करता है: सबसे बड़ी वस्तुओं को नीचे की ओर मोड़ो और उन्हें छोटे लोगों के साथ भरें। यहाँ है कि यह कैसा दिखता है। आयतों से, चौड़ी पट्टी से चौड़ी, चौड़ी चुनी जाती है, आपने यह अनुमान लगाया है, और बेतरतीब ढंग से बाईं ओर संरेखण के साथ एक दूसरे के शीर्ष पर खड़ी है। शेष लोगों को गैर-बढ़ती ऊंचाइयों द्वारा सॉर्ट किया जाता है और पहले से ही रखी गई ऊपर से बाएं से दाएं एक के बाद एक स्टैक करना शुरू करते हैं। जैसे ही उनकी कुल चौड़ाई पट्टी की आधी चौड़ाई से अधिक हो जाती है, शेष सभी एक दूसरे पर या तो बाईं ओर (पट्टी के बाएं किनारे से शुरू होकर) या दाईं ओर (मध्य से), सिद्धांत के अनुसार "जहां फिलहाल कम है।" जैसा कि आंकड़ों से देखा जा सकता है, बक्से की तुलना में इस पद्धति के साथ पुस्तकों को ढेर करना अधिक सुविधाजनक है।

स्लाटर एल्गोरिथ्म

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: विभाजन एल में दो उपविदों L1 और L2 आयतों से मिलकर होते हैं
     चौड़ाई 1/2 से अधिक और क्रमशः 1/2 पर।
  2: एल 1 में सभी आयतों को ढेर छोड़ दें जो शीर्ष पर उचित हैं
     पट्टी के निचले भाग में एक दूसरे को शुरू करना।  कम्प्यूट हस्टैक
  3: पैकिंग Hstack के ऊपर जारी रहेगी
  4: गैर-बढ़ती ऊंचाई के अनुसार L2 में आयतों को क्रमबद्ध करें
     i <n के लिए ऐसा h (Li)) h (Li + 1)
  5: Htall L2 की सूची में सबसे ऊंची आयत की ऊंचाई है।
  6: आयतों को पैक करें, बाईं ओर से दाईं ओर बाईं ओर
     पट्टी के किनारे जब तक पैक करने के लिए अपर्याप्त स्थान नहीं है
     एक आयत या सभी आयतों को पैक किया गया है
  7: एक ऊर्ध्वाधर रेखा के साथ पट्टी को दो समान खंडों में विभाजित करें।
     संभवतः एक आयत है जिसका आंतरिक अवरोधन हो सकता है
     ऊर्ध्वाधर रेखा द्वारा।
  8: Hright और Hleft दाहिनी ओर आयत की ऊँचाई हो
     (आदर। बाएं) पट्टी का आधा हिस्सा जिसके बाएं (दाएं) दाएं किनारे हैं
     ऊर्ध्वाधर रेखा से सटा हुआ है या जिसका आंतरिक अवरोधन है
     ऊर्ध्वाधर रेखा द्वारा
  9: जबकि वहाँ अनपैक आयतें हैं
 10: लंबाई की क्षैतिज रेखाएँ आधी की ओर खींचें
       आयत जिनकी ऊँचाई Hleft और Hright है
 11: सभी बाद की पैकिंग या तो बाईं ओर होगी
       या पट्टी का दाहिना खंड
 12: न्यूनतम ऊंचाई और पैक वाले सेगमेंट का चयन करें
       पट्टी के किनारे से आयताकार तक
       सभी आयतों तक ऊर्ध्वाधर रेखा
       पैक या एक आयताकार है जो फिट नहीं है
 13: जबकि अंत
 14: H = max {Hleft;  Hright}

मना करना

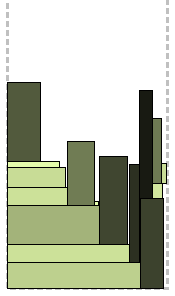
फिर एक स्तरहीन एल्गोरिथ्म जिसके लिए एक अतिरिक्त "ऊंचाई मानचित्र" पेश किया गया है:

 |  |  |  _ _ ___ |
 |  |  |  |  | _ | _ |  |  |
 |  |  | _ |  |  |  |  |
 | _ _ _ _ _ _ _ _ | |  .. | _ | _ | _ | _ _ | _ | _ _ |
  0 0 0 0 0 0 0 0 0 1 3 2 3 3 3 3

यह एक सरणी है जिसके द्वारा, पट्टी भर जाने के बाद, आप कम से कम भरे हुए क्षेत्रों और उनकी चौड़ाई को ट्रैक कर सकते हैं। शुरुआत में यह शून्य से भर जाता है। आयताकार गैर-बढ़ते, अचानक, चौड़ाई द्वारा क्रमबद्ध होते हैं। फिर, एल्गोरिथ्म के प्रत्येक चरण पर:
1. सबसे निचले क्षेत्र की स्थिति की गणना की जाती है - सरणी के न्यूनतम मूल्य का सूचकांक;
2. सबसे उपयुक्त आयत का चयन किया जाता है - सबसे पहले, यह इस क्षेत्र में फिट बैठता है, और दूसरी बात, यह इसे यथासंभव विस्तृत करता है;
3. यदि एक उपयुक्त आयत पाया जाता है, तो इसे इस क्षेत्र में एक तरीके से रखा जाता है:
3.1 क्षेत्र के बाएं किनारे पर;
3.2 एक उच्च पड़ोसी के करीब, अगर पड़ोसी में से एक पट्टी का किनारा है, तो किनारे के करीब;
3.3 कम पड़ोसी के करीब, अगर पड़ोसी में से एक पट्टी का किनारा है, तो किनारे से आगे। आयत की चौड़ाई के अनुरूप सरणी के मूल्यों के लिए, इसकी ऊंचाई को जोड़ा जाता है।
4. यदि कोई उपयुक्त आयत नहीं है, तो क्षेत्र को उसकी ऊंचाई को निकटतम किनारे की ऊंचाई तक समतल करके "भरा हुआ" है।
क्या आप पहले से ही इस एल्गोरिथ्म का उपयोग करके एक बॉट खेलने वाला टेट्रिस लिखना चाहते हैं?

बर्क एलगोरिदम

  इनपुट: आयत की संख्या n पैक की जाएगी,
        आयतों के आयाम
        {w (ली);  h (Li)} और स्ट्रिप चौड़ाई W।
 आउटपुट: पट्टी में प्राप्त पैकिंग की ऊंचाई।
  1: गैर-बढ़ती चौड़ाई के अनुसार आयतों को क्रमबद्ध करें जैसे कि w (Li) Li w (Li + 1) ≥ .. ≥ W (Ln)
  2: प्रत्येक प्लेसमेंट पॉलिसी के लिए
     (leftest, सबसे लंबा पड़ोसी, सबसे छोटा पड़ोसी) करते हैं
  3: जबकि आयताकार पैक नहीं करते हैं
  4: सबसे कम अंतर खोजें
  5: यदि w (Li) W गैपविथ तब
  6: प्लेसमेंट नीति का उपयोग करते हुए सर्वश्रेष्ठ फिटिंग आयत रखें
  7: उपयुक्त ऊंचाई तक सरणी के तत्वों को बढ़ाएं
  8: और
  9: सबसे कम पड़ोसी की ऊंचाई के लिए अंतराल बढ़ाएं
 10: अंत यदि
 11: जबकि अंत
 12: के लिए अंत
 13: सबसे बड़ी प्रविष्टि वाले सरणी के तत्व पैकिंग की कुल ऊंचाई देते हैं
 14: प्रत्येक प्लेसमेंट पॉलिसी द्वारा प्राप्त कुल पैकिंग हाइट्स की तुलना करें और सर्वश्रेष्ठ समाधान लौटाएं

कौन बेहतर है

प्रत्येक एल्गोरिदम का परिणाम बैंडविड्थ का स्तर है, कम बेहतर है। इसका अनुमान इसके इष्टतम के अनुपात से लगाया जा सकता है:

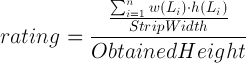
स्रोत डेटा के दो सेटों के परिणामों की तुलना करें:

	इष्टतम निर्णय	NFDH	FFDH	BFDH	KP01	एस एफ	शामिल हों	FCNR	Sleator	टिड्डी
1 सेट करें	149	0.65	0.71	0.71	0.71	0.75	0.61	0.83	0.68	0.72
2 सेट करें	140	0.66	0.77	0.77	0.78	0.77	0.70	0.84	0.51	0.71

हम देखते हैं कि फ्लोर सीलिंग एल्गोरिथ्म दोनों डेटासेट के लिए जीता है। यह ध्यान दिया जा सकता है कि स्लीटोर ने पहले सेट के लिए बहुत बेहतर परिणाम दिखाया, और इसके विपरीत, सम्मिलित हों, दूसरे के लिए अधिक उपयुक्त है। लेकिन यह सब आंकड़ों से ज्यादा कुछ नहीं है।

उपसंहार

अपने सरल सूत्रीकरण के कारण, द्विआधारी पैकेजिंग के कार्य को बड़ी संख्या में व्यावहारिक अनुप्रयोगों के लिए खींचा जा सकता है: सीधे वस्तुओं को काटना या सामग्री काटना, धन आवंटित करना, समूहों पर कार्य की योजना बनाना आदि। जीवन में कुछ परिष्कृत समस्याएं हैं, लेकिन कुछ स्थितियों को सीमित करके, आप एक खूबसूरत गणितीय मॉडल की स्थिति को कम कर सकते हैं जिसका एक अच्छा समाधान है, जो बहुपद समय में प्राप्य है। और एक बार, तितली प्रभाव के परिणामस्वरूप, परित्यक्त स्थितियां बहुत अधिक वजन ले जाएंगी और निर्णय सभी Nameless के लिए उड़ जाएगा। यह ऐसी धारणाओं के कारण है कि दुनिया अपूर्ण है।

कुछ मैं विचलित था। अगले भाग में मुझे कार्य और अपतटीय एल्गोरिदम के ऑनलाइन संस्करण के बारे में बात करने की उम्मीद है। अ छा!

प्रेरणा के स्रोत:
Nthabiseng Ntene 2 डी ओरिएंटेड स्ट्रिप पैकिंग समस्या के लिए एक एल्गोरिथम दृष्टिकोण
डेविड पिसिंगर नैकपैक समस्या
दो आयामी पैकिंग पर सर्वेक्षण
स्तर एल्गोरिथ्म और शेल्फ एल्गोरिदम (सावधानी, आंसू-नेत्र डिजाइन)

कोड (Qt):
एल्गोरिदम packager.h packager.cpp
गुई window.h window.cpp रेंडररी.ह रेंडरए.कापी । Main.cpp

UPD: ऑनलाइन एल्गोरिदम

दो आयामी पैकेजिंग के बारे में: ऑफ़लाइन एल्गोरिदम