सिंपलेक्स सियरपिन्स्की

यह लेख कंप्यूटर के बहुआयामी ग्राफिक्स के मूल गणितीय घटक से परिचित करने के लिए है। उदाहरण के रूप में सीरपिन्स्की सिंप्लेक्स का उपयोग करते हुए, लेख जटिल बहुआयामी ज्यामितीय आकृतियों के निर्माण, स्थानांतरित करने, पेश करने और प्रदर्शित करने के मुद्दों पर चर्चा करता है।
वहाँ भी चित्र, वीडियो, स्रोत हैं, और मैं आपको विश्वास दिलाता हूं कि सब कुछ बहुत सरल है, पढ़ें, में तल्लीन करें।

Sierpinski त्रिकोण क्या है, और Sierpinski पिरामिड क्या है , बहुत स्पष्ट है। लेकिन Sierpinski सिम्प्लेक्स क्या है? शुरू करने के लिए, उन लोगों के लिए जिन्होंने विकी पर नहीं पढ़ा है कि एक सिम्प्लेक्स क्या है - मैं सिर्फ इतना कहूंगा कि एक सिम्प्लेक्स एक एन-डायमेंशनल टेट्राहेड्रॉन है ( वीडियो देखें)। खैर, Sierpinski सिंप्लेक्स एक तरह का फ्रैक्टल है, जिसे त्रिकोण और Sierpinski tetrahedron के साथ सादृश्य द्वारा बनाया गया है।

एक समभुज सिंप्लेक्स का निर्माण

इस पर विश्वास न करें, लेकिन इस लेख (मेरे अनुमान के अनुसार) में यह सबसे कठिन है। लेकिन हम सभी की जरूरत n-1 आयामी अंतरिक्ष में एक दूसरे से और केंद्र से समान दूरी पर n अंक है। आगे पढ़ने से पहले, मैं दृढ़ता से यह सोचने की सलाह देता हूं कि आप ऐसे बिंदुओं का निर्माण कैसे करेंगे?

बेशक, हम ऐसे मामलों में रुचि रखते हैं जहां n> = 3, अन्यथा यह केवल दिलचस्प नहीं है। प्रत्येक nth बिंदु को पिछले सभी के आधार पर बनाया जाएगा। आरंभ करने के लिए, हमें एक नियमित समबाहु त्रिभुज बनाने की आवश्यकता है:


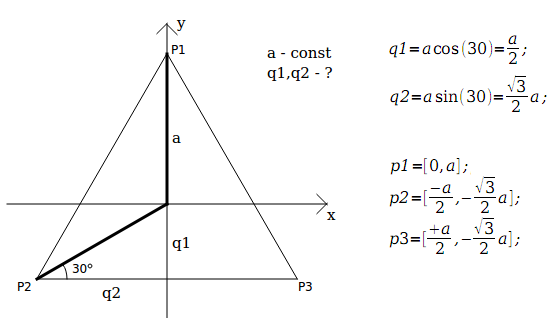
एक नया बिंदु जोड़ने के लिए, आपको एक नए आयाम (डब्ल्यू द्वारा चिह्नित) की आवश्यकता है। इस माप का परिचय देते हुए कि बिंदु अन्य सभी बिंदुओं के बराबर है, हम इस बिंदु Pn के लिए W अक्ष के साथ q1 और W अक्ष के साथ अन्य बिंदुओं के लिए -q2 सेट करते हैं। बिंदु Pn के लिए शेष अक्ष निर्देशांक शून्य छोड़ दिया जाएगा। यह क्या है? कि सभी बिंदु जो थे - एक दूसरे से और केंद्र से समान दूरी पर रहते हैं, और नया बिंदु अन्य सभी से समान है। यह केवल ऐसे q1, q2 को चुनने के लिए ही रहता है ताकि सभी बिंदु एक दूसरे से और केंद्र से समान हों।


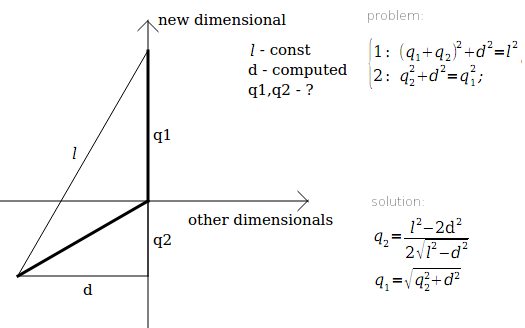
एल - बिंदुओं के बीच की दूरी - हमेशा की तरह, और त्रिकोण के निर्माण के बाद गणना की जाती है।
d - केंद्र से बिंदुओं की दूरी - परिवर्तन, और एक नया बिंदु जोड़ने से पहले गणना की जाती है।
पहला समीकरण इंगित करता है कि प्राप्त अंकों से नए तक की दूरी समान होनी चाहिए।
दूसरा यह है कि केंद्र की दूरियां समान होनी चाहिए।
दरअसल, इस तरह से हमें एक समभुज सिम्पलेक्स मिलता है।

सूत्रों का कहना है:

double c = r * sqrt(3) / 2; double l = c * 2; //distance between points points[0][0] = + 0; points[0][1] = + r; //first point points[1][0] = + c; points[1][1] = - r / 2; //second point points[2][0] = - c; points[2][1] = - r / 2; //3th point for (int i = 3; i <= dimensionalCount; i++) { double d = points[0].distanceToCenter(); double q2 = (l * l - 2 * d * d) / (2 * sqrt(l * l - d * d)); double q1 = sqrt(d * d + q2 * q2); for (int k = 0; k < i; k++) { points[k][i-1] = -q2; //set i-th dimension for all created points points[i][k] = 0; //set all calculated dimension for new point } points[i][i-1] = q1; } 

भग्न

यह नोटिस करना बहुत आसान है कि दोनों त्रिकोण (n = 2) और Sierpinski tetrahedron (n = 3) आधार आकृति से n + 1 के साथ आधार आकृति को बदलकर बनाए जाते हैं, लेकिन छोटे। प्रत्येक नए आंकड़े में, आधार आकृति के एक बिंदु को आधार के रूप में लिया जाता है, शेष बिंदु खंडों के द्रव्यमान के केंद्र होते हैं जिनमें यह बिंदु शामिल होता है। सिद्धांत रूप में, सब कुछ बहुत सरल और स्पष्ट है।

तो हम लिखते हैं:

 void rec(QVector<Simplex>& storage, const Simplex& current, int recursionDepth) { if (recursionDepth == maxRecursionDepth) storage.append(current); else { for (int i = 0; i <= n; i++) { Simplex newTriangle(current.dimensionsCount()); for (int k = 0; k <= n; k++) { if (i == k) newTriangle[k] = current[i]; else newTriangle[k] = (current[i] + current[k]) / 2.0; } rec(storage, newTriangle, recursionDepth + 1); } } } 

जैसा कि आप देख सकते हैं, अंतरिक्ष के आयाम पर भरोसा करने के लिए कहीं और नहीं है, और यह 2 डी और 3 डी दोनों के लिए सही ढंग से काम करता है:

घुमाएँ और प्रोजेक्शन

इसे घुमाना मुश्किल हो सकता है (चतुर्धातुक, मैट्रिक्स परिवर्तन), लेकिन यह बस संभव है ... हम सब कुछ बस करेंगे, क्रमिक रूप से प्रत्येक दो निर्देशांक के साथ घुमाएंगे। 2 डी के लिए, यह एक बिंदु के चारों ओर घुमाव के रूप में समझा जा सकता है, 3 डी के लिए - एक सीधी रेखा के आसपास, एनडी के लिए - (एन -2) के आसपास-आयामी स्थान। वास्तव में, रोटेशन सूत्र की गणना बहुत सरलता से की जाती है:


खैर, यह प्रोग्राम करना और भी आसान है:

  for (int i = 0; i < coordinates.count(); i++) for (int k = i + 1; k < coordinates.count(); k++) { ratio = sqrt(2 + i * coordinates.count() + k); p1 = temp[i] * cos(angle * ratio) - temp[k] * sin(angle * ratio); p2 = temp[k] * cos(angle * ratio) + temp[i] * sin(angle * ratio); temp[i] = p1; temp[k] = p2; } 

जहां अनुपात एक गुणांक है, ताकि विभिन्न दिशाओं में रोटेशन अलग-अलग गति पर हो, अधिमानतः छोरों के बिना। अस्थायी [i] - ith वर्तमान बिंदु का समन्वय।

प्रोजेक्शन बहुआयामी रिक्त स्थान के साथ काम करने का सबसे कठिन क्षण है। कई कारण हैं:
1. बहुआयामी ज्यामितीय वस्तुओं को समझने के लिए किसी का उपयोग नहीं किया जाता है।
2. भौतिकी का प्रकाशविज्ञान इस बारे में चुप है (जहाँ तक मुझे पता है)।
3. विभिन्न तरीकों का एक गुच्छा और हर कोई तस्वीर को ओवरलोड करता है, और यह स्पष्ट नहीं है कि अधिक सही क्या है।

हम सबसे सरल विधि - परिप्रेक्ष्य प्रक्षेपण लेंगे। हम (n-1) स्थान पर n-आयामी बिंदु प्रोजेक्ट करेंगे ... इस प्रकार, हर बार N को कम करने पर, हम इस बिंदु पर आते हैं कि बिंदु पहले से ही दो-आयामी या तीन-आयामी है और पहले से ही प्रदर्शित किया जा सकता है।

उदाहरण के रूप में 2 डी से 1 डी का उपयोग करते हुए, चलो परिप्रेक्ष्य प्रक्षेपण सूत्र की गणना करने का प्रयास करते हैं।


यह देखा जा सकता है कि 2 निर्देशांक और एक निश्चित स्थिर फोकस का उपयोग करके, आप 1 समन्वय बना सकते हैं। और सूत्र बहुत सरल है, जैसे कोड:

  for (int i = coordinates.count() - 1; i > 3; i--) for (int k = 0; k < i; k++) temp[k] *= focus / (focus + temp[i]); 

यह कितना सही है? आम तौर पर सही नहीं, एक बार नहीं, थोड़ा सा नहीं! लेकिन इंटरनेट पर जो है, उसे देखते हुए, कुछ इसी तरह का उपयोग अन्य प्रोग्रामर द्वारा किया जाता है। यहाँ, उदाहरण के लिए, इस प्रक्षेपण विधि द्वारा प्राप्त एक टेस्सेक्ट है :

प्रतिपादन

QPainter सबसे आसान तरीका है, जो कि विकास के वातावरण के मानक साधनों का उपयोग सामान्य रेखाओं के साथ सब कुछ खींचने के लिए होता है, बिना रोशनी के, त्रिकोण को भरने के आदि। मेरे स्रोतों में, यह डिफ़ॉल्ट रूप से चालू है, और जहां भी Qt है (विंडोज, लिनक्स, मैक ओएस ...) काम करेगा।

वास्तव में, यह है कि प्रतिपादन कोड कैसा दिखता है:

  QPoint center(this->width() / 2, this->height() / 2); foreach(const Simplex& simplex, simplexes) for (int i = 0; i < simplex.dimensionsCount() + 1; i++) for (int k = i+1; k < simplex.dimensionsCount() + 1; k++) p.drawLine(simplex[i].to2D(focus, angle) + center, simplex[k].to2D(focus, angle) + center); 

जैसा कि आप देख सकते हैं, कुछ भी सरल नहीं है ... लेकिन हमें सुंदर, सही होने की आवश्यकता है?

ओपनजीएल , डायरेक्टएक्स एक प्रगतिशील तरीका है जो आपको वास्तविक समय में हर चीज को खूबसूरती से प्रस्तुत करने की अनुमति देता है। लेकिन एक दुर्भाग्य है: पारदर्शिता के बिना कुछ भी सुंदर नहीं होगा, और इन दोनों राक्षसों की पारदर्शिता बताती है कि आपको दूर (z -> अधिकतम) से लेकर (z -> मिनट) तक प्रस्तुत करना होगा। इसके लिए, प्रत्येक फ्रेम, त्रिकोण को क्रमबद्ध करने की आवश्यकता होती है, और मेरे उदाहरण में लगभग 6000 हैं। खैर, इससे कोई फर्क नहीं पड़ता, परेशानी यह है कि सामान्य स्थिति में यह निर्धारित करना असंभव है कि कौन सा त्रिकोण करीब है और कौन सा आगे है। इसके अलावा, जब हम बहुआयामी अंतरिक्ष से प्रक्षेपण के बारे में बात करते हैं, तो हम कहते हैं कि त्रिकोण प्रतिच्छेद करते हैं। नतीजतन, उन्हें प्रत्येक पुनरावृत्ति को काटने और क्रमबद्ध करने की आवश्यकता होती है, जो पहले से ही बहुत मुश्किल है ...
मैंने इस पद्धति को लागू नहीं किया।

रे ट्रेसिंग जो डॉक्टर ने आदेश दिया है। यह तकनीक आपको अधिकतम गुणवत्ता की तस्वीर प्राप्त करने की अनुमति देगी और इसकी गति में केवल एक खामी है। लेकिन, वास्तव में, हमें वास्तविक समय की आवश्यकता नहीं है।

ट्रेसिंग के लिए, मैंने POV-Ray का उपयोग किया, जो इस कार्य के लिए आदर्श रूप से केवल इस तथ्य के लिए उपयुक्त था कि यह कमांड लाइन से चल सकता है, बिना किसी GUI के।
इस चमत्कार का उपयोग करने के लिए, मैंने एक निश्चित टेम्पलेट लिखा, जिसे प्रोग्राम आवश्यक बिंदुओं के साथ भरता है, और आउटपुट ट्रेसिंग के लिए .pov फ़ाइल तैयार है। बिंदुओं के एक सेट के आधार पर एक टेम्पलेट त्रिकोण और फ्रेम बनाता है, और इसकी संरचना में बहुत सरल है:

 #declare ppp = array[<<!!--count of points--!!>>] { <<!!--Main Array of points--!!>> }; #declare i = 0; #while(i < <<!!--count of points--!!>>) #if (vlength(ppp[i] - ppp[i+1])!=0) cylinder{ppp[i], ppp[i+1], 0.2 texture {pigment{color Gray}} } #end #if (vlength(ppp[i] - ppp[i+2])!=0) cylinder{ppp[i], ppp[i+2], 0.2 texture {pigment{color Gray}} } #end #if (vlength(ppp[i+1] - ppp[i+2])!=0) cylinder{ppp[i+1], ppp[i+2], 0.2 texture {pigment{color Gray}} } #end polygon {4 ppp[i], ppp[i+1], ppp[i+2] ,ppp[i] texture { Surface_Texture }} #declare i=i+3; #end 

दरअसल, इस टेम्पलेट के आधार पर, 1000 चित्रों को अलग-अलग मोड़ के साथ बनाया गया था, जिनसे बाद में यह वीडियो बनाया गया:


स्रोत कोड

लेख भारी धातु टीम फाइट विद फेट की लड़कियों को समर्पित है।