विकृत छवियों को पुनर्स्थापित करना छवि प्रसंस्करण कार्यों में सबसे दिलचस्प और महत्वपूर्ण समस्याओं में से एक है - दोनों सैद्धांतिक और व्यावहारिक दृष्टिकोण से। विशेष मामले अनुचित फोकस और धुंधलेपन के कारण धुंधला हो रहे हैं - ये दोष, जिनसे आप में से प्रत्येक परिचित हैं, सही करना बहुत मुश्किल है - वे लेख के विषय द्वारा चुने गए हैं। शेष विकृतियों (शोर, गलत प्रदर्शन, विरूपण) के साथ, मानव जाति ने प्रभावी ढंग से निपटना सीख लिया है, उपयुक्त उपकरण हर स्वाभिमानी फोटो संपादक में हैं।

ग्रीज़ और डिफोकस को खत्म करने के लिए व्यावहारिक रूप से कुछ भी क्यों नहीं है (अनशर मास्क की गिनती नहीं होती है) - शायद यह सिद्धांत रूप में असंभव है? वास्तव में, यह संभव है - संबंधित गणितीय उपकरण लगभग 70 साल पहले विकसित होना शुरू हुआ, लेकिन, कई अन्य छवि प्रसंस्करण एल्गोरिदम की तरह, यह सब हाल ही में व्यापक उपयोग पाया गया है। यहाँ, वाह प्रभाव के प्रदर्शन के रूप में, कुछ तस्वीरें:

मैंने यातना लीना का उपयोग नहीं किया, लेकिन वेनिस की मेरी तस्वीर मिली। सही छवि ईमानदारी से बाईं ओर से प्राप्त की जाती है, और 48-बिट प्रारूप (इस मामले में मूल छवि की 100% बहाली होगी) जैसी चाल का उपयोग किए बिना - बाईं तरफ सबसे आम पीएनजी है, कृत्रिम रूप से धुंधला। परिणाम प्रभावशाली है ... लेकिन व्यवहार में यह इतना सरल नहीं है। एक बिल्ली के तहत सिद्धांत और व्यावहारिक परिणामों की एक विस्तृत समीक्षा।
सावधानी, PNG छवियों का एक बहुत!

परिचय

चलो शुरू से। बहुत से लोग मानते हैं कि धुंधलापन एक अपरिवर्तनीय संचालन है और जानकारी अनियमित रूप से खो जाती है, क्योंकि प्रत्येक पिक्सेल एक स्पॉट में बदल जाता है, सब कुछ मिक्स हो जाता है, और एक बड़े ब्लर त्रिज्या के साथ हमें पूरी छवि में एक समान रंग मिलता है। यह पूरी तरह से सच नहीं है - सभी जानकारी बस कुछ कानून के अनुसार पुनर्वितरित की जाती है और कुछ आरक्षणों के साथ स्पष्ट रूप से बहाल की जा सकती है। धब्बा त्रिज्या की चौड़ाई के साथ एक अपवाद केवल छवि के किनारों है - वहां पूरी बहाली असंभव है।

हम इसे "उंगलियों पर" प्रदर्शित करेंगे, एक आयामी मामले के लिए एक छोटे से उदाहरण का उपयोग करते हुए - कल्पना करें कि हमारे पास मानों के साथ पिक्सेल की एक पंक्ति है:
x ₁ | x ₂ | x ₃ | x ₄ ... - मूल चित्र

विकृति के बाद, प्रत्येक पिक्सेल का मूल्य बाईं ओर के मूल्य के साथ अभिव्यक्त होता है, अर्थात। x ' _i = x _i + x _i-1 । सिद्धांत रूप में, हमें 2 से भी विभाजित होना चाहिए, लेकिन सरलता के लिए इसे छोड़ देना चाहिए। परिणामस्वरूप, हमारे पास पिक्सेल मूल्यों के साथ एक धुंधली छवि है:
x ₁ + x ₀ | x ₂ + x ₁ | x ₃ + x ₂ | x ₄ + x ₃ ... - धुंधली छवि

अब हम योजना के अनुसार श्रृंखला के अनुसार मूल्यों को क्रमिक रूप से घटाने, बहाल करने की कोशिश करेंगे - दूसरे पिक्सेल से पहला, तीसरे से दूसरा, चौथे से तीसरा और इसी तरह, हम प्राप्त करते हैं:
x ₁ + x ₀ | x ₂ - x ₀ | x ₃ + x ₀ | x ₄ - x ₀ ... - पुनर्प्राप्त की गई छवि

नतीजतन, एक धुंधली छवि के बजाय, हमें मूल छवि मिली, जिसमें पिक्सेल के लिए एक अज्ञात निरंतर x _{0 के} साथ एक वैकल्पिक संकेत जोड़ा गया था। यह पहले से ही बहुत बेहतर है - इस स्थिरांक को नेत्रहीन रूप से चुना जा सकता है, यह माना जा सकता है कि यह मूल्य x _{1 के} लगभग बराबर है, इसे स्वचालित रूप से इस तरह की कसौटी के साथ चुना जा सकता है कि पड़ोसी पिक्सल के मान "कूद" जितना संभव हो उतना कम हो, आदि। लेकिन जैसे ही हम शोर जोड़ते हैं (जो हमेशा वास्तविक छवियों में होते हैं) सब कुछ बदल जाता है। वर्णित योजना के साथ, प्रत्येक चरण में, कुल घटक को शोर का योगदान जमा होगा, जो अंत में पूरी तरह से अस्वीकार्य परिणाम दे सकता है, लेकिन, जैसा कि हमने देखा है, इस तरह के आदिम तरीके से भी बहाली काफी यथार्थवादी है।

विरूपण प्रक्रिया मॉडल

और अब चलो विकृति और बहाली की इन प्रक्रियाओं के एक अधिक औपचारिक और वैज्ञानिक विवरण पर चलते हैं। हम केवल स्केल-ब्लैक-एंड-व्हाइट छवियों को इस धारणा के तहत मानेंगे कि एक पूर्ण-रंग छवि को संसाधित करने के लिए, यह आरजीबी रंग चैनलों में से प्रत्येक के लिए सभी आवश्यक चरणों को दोहराने के लिए पर्याप्त है। हम निम्नलिखित संकेतन प्रस्तुत करते हैं:
f (x, y) - मूल अविरल छवि
h (x, y) एक विकृत कार्य है
n (x, y) - योजक शोर
जी (एक्स, वाई) विरूपण का परिणाम है, अर्थात। हम परिणाम के रूप में क्या देखते हैं (धुंधली या विकृत छवि)

हम विकृति प्रक्रिया का एक मॉडल बनाते हैं:
g (x, y) = h (x, y) * f (x, y) + n (x, y) (1)

विकृत छवि को पुनर्स्थापित करने का कार्य मूल छवि का सर्वश्रेष्ठ सन्निकटन f '(x, y) खोजना है। प्रत्येक घटक पर अधिक विस्तार से विचार करें। F (x, y) और g (x, y) के साथ सब कुछ बहुत स्पष्ट है। लेकिन फ़ंक्शन एच (एक्स, वाई ) के बारे में मुझे कुछ शब्द कहने की ज़रूरत है - यह कैसा है? विकृति की प्रक्रिया में, मूल छवि का प्रत्येक पिक्सेल डिफोकसिंग के मामले में और साधारण तेल के मामले के लिए एक सेगमेंट में बदल जाता है। या आप इसके विपरीत कह सकते हैं, कि विकृत छवि के प्रत्येक पिक्सेल को मूल छवि के एक निश्चित पड़ोस के पिक्सल से "इकट्ठा" किया जाता है। यह सब एक दूसरे पर आरोपित है और परिणामस्वरूप हमें एक विकृत छवि मिलती है। कि एक पिक्सेल को किस कानून के अनुसार नष्ट किया जाता है या एकत्र किया जाता है, इसे विकृति कार्य कहा जाता है। अन्य पर्यायवाची शब्द PSF (बिंदु प्रसार कार्य, अर्थात् एक बिंदु का वितरण कार्य), विकृत करने वाले ऑपरेटर का कोर, कर्नेल और अन्य हैं। इस फ़ंक्शन का आयाम, एक नियम के रूप में, स्वयं छवि के आयाम से कम है - उदाहरण के लिए, "उंगलियों पर" उदाहरण की प्रारंभिक परीक्षा में फ़ंक्शन का आयाम 2 था, क्योंकि प्रत्येक पिक्सेल दो से बना था।

कार्य विकृत करना

आइए देखें कि विशिष्ट विकृत कार्य क्या दिखते हैं। इसके बाद, हम Matlab टूल का उपयोग करेंगे, जो पहले से ही इस तरह के उद्देश्यों के लिए मानक बन गया है, इसमें कई प्रकार की छवि प्रसंस्करण प्रयोगों (और न केवल) के लिए आवश्यक सब कुछ शामिल है और आपको स्वयं को एल्गोरिदम पर ध्यान केंद्रित करने की अनुमति देता है, पुस्तकालयों को कार्य करने के लिए सभी नियमित काम को स्थानांतरित करता है। हालांकि, इसके लिए आपको प्रदर्शन के साथ भुगतान करना होगा। तो, पीएसएफ पर वापस, यहाँ अपनी तरह के उदाहरण हैं:

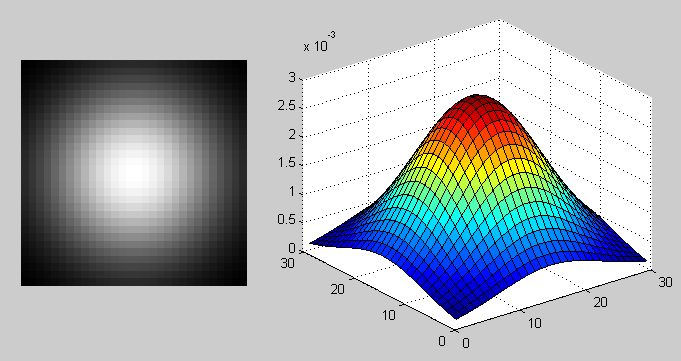विशिष्ट कार्य ('गौसियन', 30, 8) द्वारा गॉसियन कलंक के मामले में पीएसएफ;

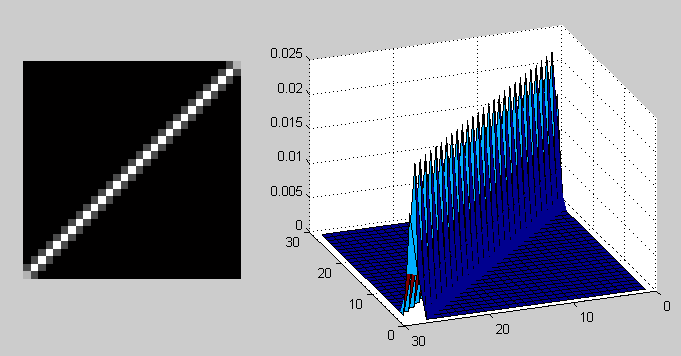विशिष्ट कार्य ('गति', 40, 45) के साथ स्नेहन के मामले में पीएसएफ;

किसी अन्य फ़ंक्शन (छवि के लिए, इस मामले में) में एक विकृत कार्य को लागू करने के संचालन को कन्वेंशन कहा जाता है, अर्थात। मूल छवि का कुछ क्षेत्र विकृत छवि के एक पिक्सेल में ढह जाता है। इसे ऑपरेटर "*" के माध्यम से निर्दिष्ट किया जाता है, सामान्य गुणा से भ्रमित होने की नहीं! आयाम M x N के साथ एक छवि f के लिए गणितीय रूप से और आयाम mxn के साथ एक विकृत कार्य h , यह इस प्रकार लिखा जाता है:

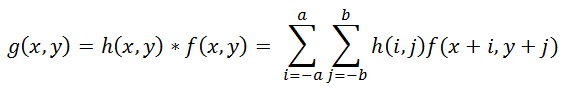
(2)

जहाँ a = (m - 1) / 2, b = (n - 1) / 2 । आक्षेप के विपरीत ऑपरेशन को विघटन कहा जाता है, और इस तरह की समस्या का समाधान बहुत ही निर्विवाद है।

शोर मॉडल

यह शोर के लिए जिम्मेदार अंतिम शब्द पर विचार करने के लिए बना हुआ है , सूत्र (1) में n (x, y )। डिजिटल सेंसर में शोर के कारण बहुत भिन्न हो सकते हैं, लेकिन मुख्य हैं थर्मल उतार-चढ़ाव और अंधेरे धाराएं। शोर मूल्य भी कई कारकों से प्रभावित होता है, जैसे कि आईएसओ मूल्य, मैट्रिक्स प्रकार, पिक्सेल आकार, तापमान, विद्युत चुम्बकीय हस्तक्षेप, आदि। ज्यादातर मामलों में, शोर गॉसियन है (जो दो मापदंडों द्वारा निर्धारित किया जाता है - औसत और फैलाव, और यह भी additive है, सहसंबंधित नहीं है) छवि के साथ और पिक्सेल के निर्देशांक पर निर्भर नहीं करता है। अंतिम तीन धारणाएं आगे के काम के लिए बहुत महत्वपूर्ण हैं।

बातचीत प्रमेय

हमें पुनर्प्राप्ति समस्या के प्रारंभिक सूत्रीकरण पर वापस लौटना चाहिए - हमें शोर को न भूलते हुए किसी तरह दृढ़ संकल्प को उलटने की आवश्यकता है। यह सूत्र (2) से देखा जा सकता है कि जी (एक्स, वाई) से एफ (एक्स, वाई) प्राप्त करना इतना आसान नहीं है - यदि आप तय करते हैं कि "हेड ऑन" क्या है, तो आपको समीकरणों की एक विशाल प्रणाली मिलती है। लेकिन फूरियर रूपांतरण हमारी सहायता के लिए आता है, हम इस पर विस्तार से ध्यान नहीं देंगे, इस विषय पर पहले ही बहुत कुछ कहा जा चुका है। तो, इस तरह के एक सजा प्रमेय है जो बताता है कि स्थानिक डोमेन में कनवल्शन ऑपरेशन आवृत्ति डोमेन में सामान्य गुणन के बराबर है (इसके अलावा, तत्व-वार गुणा, मैट्रिक्स गुणन नहीं है)। तदनुसार, उलटा कनवल्शन ऑपरेशन फ़्रीक्वेंसी डोमेन में विभाजन के बराबर है, अर्थात इसे इस प्रकार लिखा जा सकता है:

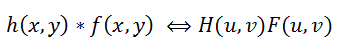
(3)

जहाँ H (u, v), F (u, v) संबंधित कार्यों के फूरियर चित्र हैं। तो सूत्र से विकृति प्रक्रिया (1) आवृत्ति डोमेन में फिर से लिखी जा सकती है:

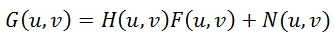
(4)

उलटा छानना

यह तुरंत इस समानता को H (u, v) में विभाजित करता है और मूल छवि का निम्नलिखित अनुमान F ^{^} (u, v) प्राप्त करता है :

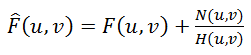
(5)
इसे उलटा फ़िल्टरिंग कहा जाता है, लेकिन व्यवहार में यह लगभग कभी काम नहीं करता है। ऐसा क्यों? इस प्रश्न का उत्तर देने के लिए, हम सूत्र (5) में अंतिम शब्द को देखते हैं - यदि फ़ंक्शन H (u, v) शून्य या शून्य के करीब मान लेता है, तो इस शब्द का योगदान प्रमुख होगा। यह लगभग हमेशा वास्तविक उदाहरणों में पाया जाता है - यह समझाने के लिए, हमें याद दिलाएं कि फूरियर रूपांतरण के बाद स्पेक्ट्रम कैसा दिखता है।

मूल छवि लें,

हम इसे ग्रेस्केल में बदल देते हैं और, मतलब का उपयोग करके, हमें स्पेक्ट्रम मिलता है:

% Load image I = imread('image_src.png'); figure(1); imshow(I); title(' '); % Convert image into grayscale I = rgb2gray(I); % Compute Fourier Transform and center it fftRes = fftshift(fft2(I)); % Show result figure(2); imshow(mat2gray(log(1+abs(fftRes)))); title('FFT -   ( )'); figure(3); imshow(mat2gray(angle(fftRes))); title('FFT -  ');

नतीजतन, हम दो घटक प्राप्त करते हैं: आयाम और चरण स्पेक्ट्रा। वैसे, कई लोग चरण के बारे में भूल जाते हैं। कृपया ध्यान दें कि आयाम स्पेक्ट्रम एक लघुगणकीय पैमाने पर दिखाया गया है, जैसा कि इसके मूल्य बहुत भिन्न होते हैं - परिमाण के कई आदेशों के अनुसार, केंद्र में अधिकतम मूल्य (लाखों के क्रम के) होते हैं और केंद्र से दूर जाते ही वे लगभग शून्य हो जाते हैं। यह इस वजह से है कि उलटा फ़िल्टरिंग केवल शून्य या लगभग शून्य शोर मूल्यों पर काम करेगा। आइए हम निम्नलिखित स्क्रिप्ट का उपयोग करते हुए इसे प्रदर्शित करते हैं:

 % Load image I = im2double(imread('image_src.png')); figure(1); imshow(I); title(' '); % Blur image Blurred = imfilter(I, PSF,'circular','conv' ); figure(2); imshow(Blurred); title(' '); % Add noise noise_mean = 0; noise_var = 0.0; Blurred = imnoise(Blurred, 'gaussian', noise_mean, noise_var); % Deconvolution figure(3); imshow(deconvwnr(Blurred, PSF, 0)); title('');

  शोर_वर = 0.0000001 शोर_वर = 0.000005

यह स्पष्ट रूप से देखा जाता है कि बहुत छोटे शोर के अलावा महत्वपूर्ण हस्तक्षेप होता है, जो विधि के व्यावहारिक अनुप्रयोग को बहुत सीमित करता है।

विघटन के लिए मौजूदा दृष्टिकोण

लेकिन ऐसे दृष्टिकोण हैं जो छवि में शोर की उपस्थिति को ध्यान में रखते हैं - सबसे प्रसिद्ध और बहुत पहले में से एक है वीनर फ़िल्टर। वह छवि और शोर को यादृच्छिक प्रक्रियाओं के रूप में मानता है और इस तरह के एक अनुमान f ' को अविभाजित छवि f के लिए खोजता है ताकि इन मूल्यों का मानक विचलन न्यूनतम हो। इस विचलन की न्यूनतम आवृत्ति डोमेन में फ़ंक्शन पर प्राप्त की जाती है:

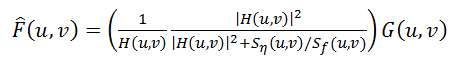
(6)
यह परिणाम 1942 में वीनर द्वारा प्राप्त किया गया था। हमने यहां एक विस्तृत निष्कर्ष नहीं दिया है, जो लोग रुचि रखते हैं वे इसे यहां देख सकते हैं। यहां फ़ंक्शन S, क्रमशः शोर और मूल छवि के ऊर्जा स्पेक्ट्रा को दर्शाता है - चूंकि इन मात्राओं को शायद ही कभी जाना जाता है, अंश S _n / S _{f को} कुछ निरंतर K द्वारा प्रतिस्थापित किया जाता है, जिसे लगभग संकेत-से-शोर अनुपात के रूप में वर्णित किया जा सकता है।

अगली विधि "एक लिंक के साथ कम से कम चौरसाई" चौरसाई है, अन्य नाम: "Tikhonov छानने", "Tikhonov नियमितीकरण"। उनका विचार मैट्रिक्स के रूप में समस्या को इसी अनुकूलन समस्या के आगे समाधान के साथ तैयार करना है। इस समाधान के रूप में लिखा है:

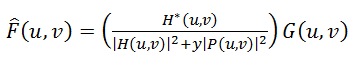
(7)
जहां y नियमितीकरण पैरामीटर है, और P (u, v) लैपलैस ऑपरेटर (3 * 3 मैट्रिसेस) का फूरियर रूपांतरण है।

एक और दिलचस्प दृष्टिकोण रिचर्डसन (1972) और लुसी (1974) द्वारा स्वतंत्र रूप से सुझाया गया था। विधि को "लुसी-रिचर्डसन विधि" कहा जाता है। इसकी विशिष्ट विशेषता यह है कि यह पहले तीन के विपरीत गैर-रैखिक है, जो संभावित रूप से सर्वोत्तम परिणाम दे सकता है। दूसरी विशेषता - विधि क्रमशः पुनरावृत्ति है, पुनरावृत्तियों को रोकने के लिए कसौटी के साथ कठिनाइयाँ उत्पन्न होती हैं। मूल विचार अधिकतम संभावना पद्धति का उपयोग करना है जिसके लिए यह माना जाता है कि छवि पॉइसन वितरण के अधीन है। फूरियर रूपांतरण का उपयोग किए बिना, गणना के लिए सूत्र काफी सरल हैं - सब कुछ स्थानिक डोमेन में किया जाता है:

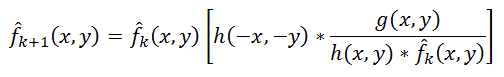
(8)
यहाँ, प्रतीक "*", पहले की तरह, सजा ऑपरेशन को दर्शाता है। खगोलीय तस्वीरों को संसाधित करने के लिए कार्यक्रमों में इस पद्धति का व्यापक रूप से उपयोग किया जाता है - उनमें डेकोवोल्यूशन का उपयोग (अनशर मास्क के बजाय, जैसा कि फोटो संपादकों में होता है) डी वास्तविक मानक है। एक उदाहरण एस्ट्रा इमेज है, यहां डिकॉन्वॉल्यूशन के उदाहरण हैं। विधि की कम्प्यूटेशनल जटिलता बहुत बड़ी है - एक औसत तस्वीर प्रसंस्करण, पुनरावृत्तियों की संख्या के आधार पर, कई घंटे और दिन भी लग सकते हैं।

विचाराधीन अंतिम विधि, या यों कहें, विधियों का एक पूरा परिवार, जो अब सक्रिय रूप से विकसित और विकसित हो रहा है, अंधा विघटन है। पिछले सभी तरीकों में, यह मान लिया गया था कि PSF का विकृत कार्य वास्तव में ज्ञात है, वास्तव में ऐसा नहीं है, आमतौर पर PSF को केवल दृश्य विकृतियों की प्रकृति से ही जाना जाता है। ब्लाइंड डीकनोवोल्यूशन इसे ध्यान में रखने का एक प्रयास है। सिद्धांत काफी सरल है, यदि आप विवरण में नहीं जाते हैं, तो पीएसएफ का पहला सन्निकटन चुना जाता है, फिर एक विधि का उपयोग करके डीकोनवोल्यूशन किया जाता है, जिसके बाद गुणवत्ता स्तर कुछ मानदंड द्वारा निर्धारित किया जाता है, पीएसएफ फ़ंक्शन को इसके आधार पर परिष्कृत किया जाता है, और वांछित परिणाम प्राप्त होने तक पुनरावृत्ति दोहराई जाती है।

अभ्यास

अब, सिद्धांत के साथ, सब कुछ - चलो अभ्यास पर आगे बढ़ते हैं, छवि पर सूचीबद्ध तरीकों की तुलना कृत्रिम धुंधला और शोर के साथ करते हैं।

 % Load image I = im2double(imread('image_src.png')); figure(1); imshow(I); title(' '); % Blur image PSF = fspecial('disk', 15); Blurred = imfilter(I, PSF,'circular','conv' ); % Add noise noise_mean = 0; noise_var = 0.00001; Blurred = imnoise(Blurred, 'gaussian', noise_mean, noise_var); figure(2); imshow(Blurred); title(' '); estimated_nsr = noise_var / var(Blurred(:)); % Restore image figure(3), imshow(deconvwnr(Blurred, PSF, estimated_nsr)), title('Wiener'); figure(4); imshow(deconvreg(Blurred, PSF)); title('Regul'); figure(5); imshow(deconvblind(Blurred, PSF, 100)); title('Blind'); figure(6); imshow(deconvlucy(Blurred, PSF, 100)); title('Lucy');

परिणाम:

वीनर फिल्टर

तिखोनोव नियमितीकरण

लुसी रिचर्डसन फ़िल्टर

अंधा विघटन

निष्कर्ष

और पहले भाग के अंत में, हम वास्तविक चित्रों के कुछ उदाहरणों को स्पर्श करेंगे। इससे पहले, सभी विकृतियां कृत्रिम थीं, जो निश्चित रूप से चलने और अध्ययन करने के लिए अच्छी है, लेकिन यह देखना बहुत दिलचस्प है कि यह सब वास्तविक तस्वीरों के साथ कैसे काम करेगा। कैनन 500D DSLR के साथ इस तरह की तस्वीर का एक उदाहरण यहां दिया गया है:

इसके बाद, एक साधारण स्क्रिप्ट चलाएँ:

 % Load image I = im2double(imread('IMG_REAL.PNG')); figure(1); imshow(I); title(' '); %PSF PSF = fspecial('disk', 8); noise_mean = 0; noise_var = 0.0001; estimated_nsr = noise_var / var(I(:)); I = edgetaper(I, PSF); figure(2); imshow(deconvwnr(I, PSF, estimated_nsr)); title('');

और हमें निम्नलिखित परिणाम मिलते हैं:

जैसा कि आप देख सकते हैं, छवि पर नए विवरण दिखाई दिए, स्पष्टता बहुत अधिक हो गई, हालांकि विपरीत सीमाओं पर "रिंगिंग" के रूप में हस्तक्षेप दिखाई दिया।

और वास्तविक तेल के साथ एक उदाहरण - इसके कार्यान्वयन के लिए, कैमरा एक तिपाई पर लगाया गया था, एक अपेक्षाकृत धीमी शटर गति सेट की गई थी और जिस समय शटर जारी किया गया था, एक समान गति प्राप्त की गई थी;

स्क्रिप्ट उसी के बारे में है, केवल PSF प्रकार अब "गति" है:

 % Load image I = im2double(imread('IMG_REAL_motion_blur.PNG')); figure(1); imshow(I); title(' '); %PSF PSF = fspecial('motion', 14, 0); noise_mean = 0; noise_var = 0.0001; estimated_nsr = noise_var / var(I(:)); I = edgetaper(I, PSF); figure(2); imshow(deconvwnr(I, PSF, estimated_nsr)); title('');

परिणाम:

गुणवत्ता, फिर से, स्पष्ट रूप से सुधार हुआ है - खिड़कियों और कारों पर फ्रेम अलग-अलग हो गए हैं। कलाकृतियां पहले से खराब हो चुके उदाहरण से अलग हैं।

इस दिलचस्प और पहले भाग को खत्म करने पर।
दूसरे भाग में, मैं वास्तविक छवियों के प्रसंस्करण की समस्याओं पर ध्यान केंद्रित करूँगा - पीएसएफ का निर्माण करना और उनका मूल्यांकन करना, अधिक जटिल और उन्नत डिकॉन्वोलुशन तकनीकों पर विचार करना, दोषों को समाप्त करने के तरीके, रिंगिंग की समीक्षा करना और मौजूदा सॉफ़्टवेयर की तुलना करना, और बहुत कुछ।

PS नहीं बहुत पहले फ़ोटोशॉप के नए संस्करण में धुंधली तस्वीरों को ठीक करने के बारे में हब पर एक लेख प्रकाशित हुआ था
जो लोग ग्रीस हटाने के लिए एक समान तकनीक के साथ खेलना चाहते हैं (शायद फ़ोटोशॉप में इसका उपयोग किया जाएगा), आप इस लिंक का उपयोग एप्लिकेशन के डेमो संस्करण को डाउनलोड करने , रिकवरी के उदाहरण देखने और ऑपरेशन के सिद्धांत के बारे में पढ़ने के लिए कर सकते हैं ।

साहित्य

गोंजालेज आर।, वुड्स आर। डिजिटल इमेज प्रोसेसिंग
MATLAB में गोन्डालेज आर।, वुड्स आर।, एडडिंस एस। डिजिटल इमेज प्रोसेसिंग

UPD: कंटीन्यूएशन लिंक

व्लादिमीर याज़िकोव

Defocused और धुंधली छवियों को पुनर्स्थापित करना