समय-समय पर, अस्थायी-बिंदु अंकगणित की जटिलताओं के बारे में
अद्भुत लेख हब पर दिखाई देते हैं। दरअसल, उल्लिखित प्रकाशन समस्या से निपटने की कोशिश करते समय पढ़े गए पहले स्रोतों में से एक था। यह तुरंत स्पष्ट नहीं हुआ, लेकिन फिर भी, तंत्रिका कनेक्शन का संगठन किसी तरह सुव्यवस्थित था। बिंदु पर पहुँचो।
समस्या एक परियोजना के ढांचे के भीतर गणनाओं और एक झरझरा माध्यम के हाइड्रोडायनामिक्स पर भविष्य के मास्टर की थीसिस के दौरान बनाई गई थी। मैं यह नहीं छिपाऊंगा कि मूल रूप से लेखक की व्यक्तिगत वक्रता में छिपी हुई हैं और छोटी संख्या के प्रसंस्करण के बारे में आम तौर पर ज्ञात सुझावों की उपेक्षा, लेकिन फिर भी, यह काफी दिलचस्प टिप्पणियों और विचारों का कारण बना।
यदि हम भौतिक सार को छोड़ देते हैं, तो समस्या को सात आंशिक अंतर समीकरणों की एक प्रणाली को हल करने की आवश्यकता है। जल्दी से नहीं कहा गया, कोई विशेष कठिनाई नहीं है - हम एक स्पष्ट परिमित-अंतर योजना लिखते हैं, इसे ओपनएमपी के साथ समानांतर करते हैं और अंतिम सिंटैक्टिक डिबगिंग और गति अनुकूलन के बाद
"मशीन सरसराहट करने लगती है ।
"कम्प्यूटिंग विन्यास: बोर्ड पर एक कोर 2 डुओ 1.8 गीगाहर्ट्ज के साथ एक एचपी 550 का प्रीव्यू, उबंटू 11.04 पर चल रहा है।
कम्पाइलर: gfortran 4.5.2 और इंटेल फोरट्रान कंपाइलर 12.1.0।
प्रारंभिक परिस्थितियों में, यह माना जाता है कि कम्प्यूटेशनल डोमेन के अंदर तरल अवस्था में पानी नहीं है - यह चरण परिवर्तनों की प्रक्रिया में प्रकट होता है। और यह अनुपस्थिति थी जिसने हमारे प्रदर्शन में एक प्रमुख भूमिका निभाई।
लिहाजा, इलाके में पानी नहीं है। प्रारंभिक स्थिति में आप क्या लिखना चाहते हैं? स्वाभाविक रूप से, 0.0D + 00 तुरंत लिखा गया था (कार्यक्रम वास्तविक संख्या की दोहरी सटीकता के साथ लिखा गया था)। प्रारंभिक चरणों में गणना मशीन शून्य के तत्काल आसपास के क्षेत्र में जाती है। परिणाम क्या हैं? आइए चार्ट को देखें:
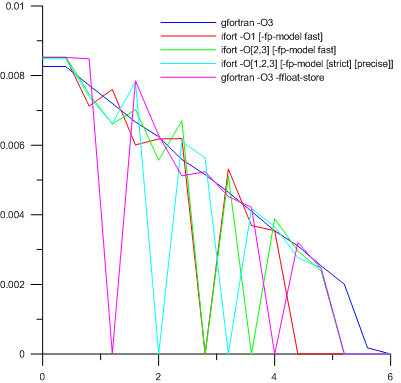
यह मॉडल के भौतिक समय के एक दिन बाद की तुलना में थोड़ा अधिक समय के बाद कम्प्यूटेशनल डोमेन के सबसे दिलचस्प हिस्से में समन्वय के साथ छिद्र जल संतृप्ति के वितरण को दर्शाता है।
चार्ट की किंवदंती में हस्ताक्षरों के बारे में आवश्यक विषयांतर: कुल मिलाकर, 18 अलग-अलग कुंजी संयोजनों का परीक्षण किया गया (6 गोरफरान और इफोर्ट के लिए 12), लेकिन उनमें से कई ने बिल्कुल समान परिणाम दिए, और इसलिए संयुक्त थे। किंवदंती में वर्ग कोष्ठक का मतलब है कि उनमें संलग्न किसी भी विकल्प को लिखा जा सकता है। उदाहरण के लिए, "एन्क्रिप्शन" -ओ [1,2,3] [-fp- मॉडल [सख्त] [सटीक]] का अर्थ है कि संकलक का उपयोग सभी संभावित स्तरों के अनुकूलन के साथ किया गया था, और एक फ़्लोटिंग-पॉइंट मॉडल को शामिल किया जा सकता है। (इसे शामिल नहीं किया जा सका)। तीन विकल्प (दो-एफपी-मॉडल और इसके बिना एक) तीन अनुकूलन स्तरों से गुणा किए जाते हैं - कुल नौ संयोजन। सब के सब बराबर हो गए।और अब परिणाम। IEEE 754 मानक (-ffloat-store key) के अनुपालन को सक्षम किए बिना केवल यथार्थवादी और शारीरिक रूप से कुछ संभव प्राप्त किया गया था। बाकी लाइनों की अव्यवस्था में भौतिक अर्थ की एक बूंद नहीं होती है, क्योंकि गणितीय रूप से भी समीकरण इसकी अनुमति नहीं देते हैं। अंतर योजना की प्रारंभिक संदिग्ध अस्थिरता उचित थी, क्योंकि इससे निपटने के किसी भी तरीके ने सफलता नहीं दिलाई।
यह देखा गया कि प्रारंभिक क्षण में पानी की उपस्थिति में स्कोर स्थिर रहता है और विकल्प और संकलक के बीच अंतर छठे महत्वपूर्ण अंक के आसपास के क्षेत्र में छिपे हुए हैं। और तब से प्राप्त ग्राफ़ों को देखते हुए, परिमाण के विशिष्ट आदेश 1.0e-2 के क्षेत्र में होने चाहिए, फिर एक निश्चित नॉनज़ेरो मूल्य, लेकिन बहुत छोटा, प्रारंभिक स्थिति में अंकित किया गया था। चयन यह स्थापित करने में कामयाब रहा कि 8-बाइट असली के लिए कम से कम 1.0e-21 होना चाहिए। और फिर:
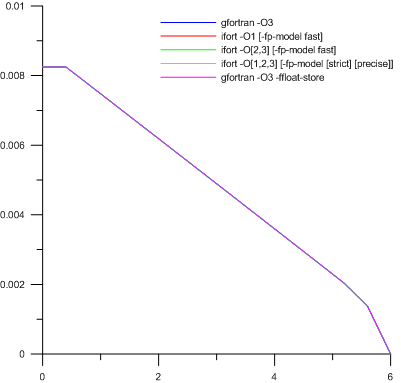
हां, यहां, जैसा कि किंवदंती में लिखा गया है, वास्तव में पांच रेखांकन हैं। बस यह है कि हम छठे महत्वपूर्ण अंक के भीतर बहुत अंतर पाते हैं।
कारणों? यह काफी स्पष्ट है। वे बड़ी और छोटी संख्या के एक साथ प्रसंस्करण की जटिलताओं में निहित हैं। और तथ्य यह है कि घटना इसके दायरे में बहुत महत्वपूर्ण है, सामान्य रूप से, अपेक्षित थी। लेकिन, सबसे पहले, इंटेल की ओर से वास्तव में एक उत्कृष्ट उपकरण की अस्थिरता 4.5.2 के सापेक्ष सफलता की पृष्ठभूमि के खिलाफ ब्याज की है। यह ध्यान देने योग्य है कि इसी तरह की समस्याएँ गफ़रन 4.1.2 के पुराने संस्करण पर गणना के दौरान भी पाई गई थीं, जिसमें ऑप्टिमाइज़ेशन सक्षम था और सुलभ क्लस्टर (स्लैमड64 रनिंग) पर स्थापित अन्य विकल्पों के बिना, लेकिन तब उन्हें ध्यान नहीं दिया गया था।
काफी हद तक, IEEE 754 के अनुपालन ने गैफरान के लिए महत्वपूर्ण भूमिका निभाई। इसके बिना, स्कोर काफी स्थिर और सटीक है। इंटेल के दिमाग की उपज के लिए, यह इतना महत्वपूर्ण नहीं था, क्योंकि यह वैसे भी सही ढंग से काम नहीं करता था।
इसलिए, उसने जो देखा उसके कारणों के बारे में निष्कर्ष और विचार।
- देखे गए गणना व्यवहार के कारण की भूमिका के लिए सबसे अधिक संभावना वाला उम्मीदवार गोल संख्याओं की सूक्ष्मता लगता है। क्योंकि मूल्य के प्रारंभिक वितरण में शून्य पर सेट किया जाता है, फिर पहले चरणों में गणना लगभग मशीन सटीकता की सीमा पर की जाती है। तदनुसार, यह ध्यान देने योग्य त्रुटियों के संचय की ओर जाता है, जो अंतिम परिणाम में दिखाई देते हैं।
- एल्गोरिथ्म में सटीकता के नुकसान भी होते हैं, जाहिर है, इस तथ्य से कि सात आंशिक अंतर समीकरणों की एक आयामी प्रणाली को हल किया जाता है, जिनमें से प्रत्येक में चर अपने स्वयं के विशिष्ट मूल्य होते हैं जो दूसरों से काफी भिन्न होते हैं। स्केल कारकों के सही विकल्प के साथ, समीकरणों के एक आयामहीन प्रणाली में, सभी चर के मूल्यों को प्राप्त करने के लिए, जो करीब हैं, कम से कम परिमाण के क्रम में, हालांकि डेरिवेटिव के सामने छोटे प्रारंभिक गुणांक प्रणाली को आयाम देने के शुरुआती प्रयासों के दौरान उत्पन्न हुए, जो इस प्रक्रिया को मना करने का कारण था।
- फ्लोइंग प्वाइंट मानक का पालन नहीं करने वाले गैफरान का प्रश्न स्वीकार्य परिणाम देने में सक्षम है, खुला रहता है। मानक से भिन्न कुछ स्वयं के गोल नियमों के अस्तित्व को मानना उचित है, जो एक स्थिर खाते के रखरखाव के साथ-साथ संकलक के विकास के दौरान उनके सुधार और शोधन को सुनिश्चित करते हैं। "गलतियों का नाजुक संतुलन" या दृष्टिकोण का विचारशील सुधार? काश, टूलकिट के बारे में ज्ञान के मेरे स्तर पर मुख्य रूप से संकलक के उपयोग के उद्देश्य से, उनका परीक्षण करने और गुणों का अध्ययन करने के बजाय, यह अज्ञात है। लेकिन यह आपको लगता है और एक विश्वविद्यालय में संख्यात्मक तरीकों में प्रशिक्षण के पहले चरणों में दिए गए कार्यक्रमों में कुछ स्थानों पर सटीकता की संभावित हानि के बारे में चेतावनी को याद करता है।
विलियम काहन द्वारा "फ्लोटिंग पॉइंट पैरानोया" के
फोरट्रान संस्करण का उपयोग करके IEEE 754 के अनुपालन के लिए कंपाइलरों का परीक्षण किया गया था।