पुनरावर्ती कार्य - अपना स्वयं का गणित (स्काला) बनाना

शुभ दोपहर, हब्र!

इस दिखावटी शीर्षक के साथ, मैं कई कलन मॉडल ( पुनरावर्ती मॉडल) - पुनरावर्ती कार्यों में से एक के बारे में एक लेख शुरू करना चाहता हूं। इस पोस्ट के पहले भाग में हम विश्लेषण करेंगे (संक्षेप में, क्योंकि विकिपीडिया पर सब कुछ विस्तृत है) इस मॉडल के सैद्धांतिक घटक (आदिम पुनरावर्तन), दूसरे भाग में हम स्काला भाषा का उपयोग करके इस मॉडल (आंशिक रूप से) को लागू करने का प्रयास करेंगे।

1. पुनरावर्ती कार्य - यह क्या है?

हर कोई वाक्यांश "ट्यूरिंग मशीन" जानता है - एक ब्रिटिश गणितज्ञ, तर्कशास्त्री, क्रिप्टोग्राफर और सिर्फ एक अच्छे व्यक्ति एलन ट्यूरिंग द्वारा बनाया गया एक कलन मॉडल। यह मॉडल कई के बीच सबसे प्रसिद्ध और लोकप्रिय कलन मॉडल में से एक है । हालाँकि, हाल ही में अन्य मॉडल जैसे लैम्ब्डा कैलकुलस और म्यू रिकर्सन को लोकप्रिय बनाया जाने लगा है।

और फिर भी, एक पुनरावर्ती कार्य क्या है?
कल्पना कीजिए कि आपके सामने एक अमूर्त कंप्यूटर है जो दो संख्याओं को जोड़ना, घटाना, अंतर करना और एकीकृत करने जैसे संचालन (अभी तक) नहीं जानता है। ऐसी मशीन के साथ कैसे काम करें? कैसे उसे गिनती करने के लिए सिखाने के लिए?
शुरू करने के लिए, हम उस बुनियादी कार्यक्षमता को परिभाषित करते हैं जो इस मशीन के पास होनी चाहिए:

• बुनियादी गणितीय कार्यों का एक सेट:
  
  - शून्य (x) = 0: प्रत्येक दिए गए तर्क x के लिए, फ़ंक्शन 0 देता है
  
  - Succ (x) = x + 1: प्रत्येक दिए गए x के लिए, फ़ंक्शन x + 1 देता है
  
  - प्रक्षेपण कार्यों का परिवार जहाँ 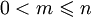: किसी भी n तर्क के लिए m स्थिति पर खड़ा होता है।
  
• उन कार्यों का एक सेट जो हम इन कार्यों पर लागू कर सकते हैं:
  
  - कार्यों की संरचना (सुपरपोजिशन): (f • g) (x) = f (g (x));
  
  - आदिम पुनरावर्तन: एन वेरिएबल्स का एक फ़ंक्शन f (X1, x2, ..., xn) हो और n / 2 वेरिएबल्स का फ़ंक्शन g (X1, X2, ..., Xn, Xn + 1, Xn + 2) हो। । तब हम n + 1 चर के फ़ंक्शन h (X1, X2, .... Xn, Xn + 1) को परिभाषित कर सकते हैं:
  
  h (X1, X2, ..., Xn, 0) = f (X1, X2, ..., Xn);
  h (X1, X2, ..., Xn, i + 1) = g (X1, X2, ..., Xn, i, h (X1, X2, ..., Xn, i));
  

वह सब जो हमारा अमूर्त कंप्यूटर कर सकता है। इस सूची में मुख्य बात, आपने अनुमान लगाया, यह आदिम पुनरावृत्ति है। इसे स्पष्ट करने के लिए, हमने अपने आप को कार्य निर्धारित किया है, उदाहरण के लिए, दो संख्याओं को जोड़ने के कार्य को कार्यान्वित करने के लिए a और b:

सम (ए, बी):
सम (a, 0) = I (a);
Sum (a, i + 1) = Succ (F (a, i, Sum (, i))) जहाँ F तीसरे तर्क का प्रक्षेपण है, अर्थात इस स्थिति में F, Sum (a, i) को लौटाएगा;

वह सब है! अब हम दो नंबर जोड़ सकते हैं और हम इस बारे में बहुत खुश हैं।
वैसे, शायद किसी के पास एक सवाल है, सुम (ए, आई + 1) को पेंट करना इतना मुश्किल क्यों है, और सिर्फ सुम (ए, आई + 1) = सुक (सु (ए, आई)) क्यों नहीं लिखना है। मैं उत्तर देता हूं: परिभाषा के अनुसार, एक पुनरावर्ती फ़ंक्शन में वांछित फ़ंक्शन के सभी तर्कों (पुनरावृत्तियों को छोड़कर) के रूप में होना चाहिए (हमारे मामले में, यह भी है), पुनरावृत्ति तर्क भी, एक (हमारे मामले में, यह i) से कम है, और वास्तव में पुनरावर्ती कॉल सम ( , मैं)। यह गैर-आदिम पुनरावृत्ति (दो या अधिक तर्कों का अनुसरण करता है) के साथ काम करने में सक्षम होने के लिए किया जाता है।

जैसा कि आप समझते हैं, उसी तरह हम निषेध, डिग्री आदि का कार्य बना सकते हैं। इन सभी उदाहरणों को विकिपीडिया पर बहुत अच्छी तरह से चित्रित किया गया है, और हम उन्हें लेख के दूसरे भाग में लागू करेंगे। किसी भी मामले में, हम पहले से ही आदिम पुनरावर्ती कार्यों के एक अनंत सेट को परिभाषित कर सकते हैं:

F = {f0, f1, f2, f3, ...} इस प्रकार परिभाषित कार्यों का एक अनंत गणनीय सेट है:

f0 (0, y) = Succ (y);
f [n + 1] (x, y): f [n + 1] (0, y) = y; f [n + 1] (i + 1, y) = fn (y, f [n + 1] (i, y));

यह आदिम पुनरावृत्ति है।
मैं गहराई से नहीं जीता और यह बताता हूं कि μ- पुनरावर्ती कार्य क्या है , विकिपीडिया पर सब कुछ बहुत अच्छी तरह से चित्रित किया गया है, खासकर जब से आदिम पुनरावृत्ति हमारे लिए अपना स्वयं का ... गणित लागू करना शुरू करने के लिए पर्याप्त है!

2. स्केला पर आदिम पुनरावृत्ति

सबसे पहले, हमें यह निर्धारित करने की आवश्यकता है कि संख्या क्या है? एक सार वर्ग बनाएँ MyNumber:

abstract class MyNumber { val isNatural: Boolean val isNeg: Boolean val isZero: Boolean val isInf: Boolean def +(b: MyNumber): MyNumber def -(b: MyNumber): MyNumber def *(b: MyNumber): MyNumber def /(b: MyNumber): MyNumber def ^(b: MyNumber): MyNumber def <(b: MyNumber): Boolean def >(b: MyNumber): Boolean def ==(b: MyNumber): Boolean def neg: MyNumber def abs: MyNumber def pre: MyInteger def suc: MyInteger val num: MyInteger val denum: MyInteger def gcd(b: MyNumber): MyNumber def mod(b: MyInteger): MyNumber override def toString(): String def toInteger: MyInteger = if(isNatural) this.asInstanceOf[MyInteger] else (num / denum).asInstanceOf[MyInteger] def toFraction: Fraction = if(isNatural) new Fraction(this.toInteger) else this.asInstanceOf[Fraction] } 

जैसा कि पहले ही देखा जा चुका है, हमारे पास दो बाल वर्ग, अंश और MyInteger होंगे:

 abstract class MyInteger extends MyNumber { val isNatural = true val isNeg: Boolean val isZero: Boolean val isInf: Boolean def +(b: MyNumber): MyNumber = if (b.isNatural) this plusInt b.toInteger else this plusFrac b.toFraction protected def plusInt(b: MyInteger): MyNumber private def plusFrac(b: Fraction): MyNumber = this.toFraction + b def -(b: MyNumber): MyNumber = if (b.isNatural) this minusInt b.toInteger else this minusFrac b.toFraction protected def minusInt(b: MyInteger): MyNumber private def minusFrac(b: Fraction): MyNumber = this.toFraction - b def *(b: MyNumber): MyNumber = if (b.isNatural) this multInt b.toInteger else this multFrac b.toFraction protected def multInt(b: MyInteger): MyNumber private def multFrac(b: Fraction): MyNumber = this.toFraction * b def /(b: MyNumber): MyNumber = if (b.isNatural) this divInt b.toInteger else this divFrac b.toFraction protected def divInt(b: MyInteger): MyNumber private def divFrac(b: Fraction): MyNumber = this.toFraction / b def ^(b: MyNumber): MyNumber = if (b.isNatural) this powInt b.toInteger else this powFrac b.toFraction protected def powInt(b: MyInteger): MyNumber protected def powFrac(b: Fraction): MyNumber //TODO def <(b: MyNumber): Boolean = if (b.isNatural) this lessThanInt b.toInteger else this lessThanFrac b.toFraction protected def lessThanInt(b: MyInteger): Boolean private def lessThanFrac(b: Fraction): Boolean = this.toFraction < b def >(b: MyNumber): Boolean = if (b.isNatural) this biggerThanInt b.toInteger else this biggerThanFrac b.toFraction protected def biggerThanInt(b: MyInteger): Boolean private def biggerThanFrac(b: Fraction): Boolean = this.toFraction > b def ==(b: MyNumber): Boolean = if (b.isNatural) this equalsInt b.toInteger else this equalsFrac b.toFraction protected def equalsInt(b: MyInteger): Boolean private def equalsFrac(b: Fraction): Boolean = this.toFraction == b def pre: MyInteger def suc: MyInteger val num: MyInteger = null val denum: MyInteger = null def neg: MyNumber def abs: MyNumber = if (!isNeg || isZero) this else this neg def gcd(b: MyNumber): MyNumber = if (b.isNatural) this gcdPrivate b.abs.toInteger else (new Zero).pre private def gcdPrivate(b: MyNumber): MyNumber = { def iter(a: MyNumber, b: MyNumber): MyNumber = { if (b == (new Zero)) a else iter(b, a.toInteger mod b.toInteger) } iter(this, b) } def mod(b: MyInteger): MyNumber = { def iter(a: MyNumber, b: MyNumber): MyNumber = { if (b.isNeg) this mod b.abs.toInteger else if (!b.isNatural) (new Zero).pre else if (a < b) if (a.isNeg) a + b else a else iter(if (a.isNeg) a + b else a - b, b) } iter(this, b) } override def toString: String = { def iter(nb: MyInteger, accu: Int): Int = { if (nb isZero) accu else if (nb isNeg) iter(nb.suc.toInteger, accu - 1) else iter(nb.pre.toInteger, accu + 1) } if(this.isInf) "Inf" else iter(this, 0).toString() } } 

Integer को परिभाषित करने के लिए, हमें निम्नलिखित संख्या (Suc), पिछली (Pre), शून्य (शून्य) और अनंत (PosInf) की अवधारणा की आवश्यकता है:

 class Zero extends MyInteger { val isZero = true val isNeg = false val isInf = false protected def plusInt(b: MyInteger): MyNumber = b protected def minusInt(b: MyInteger): MyNumber = b neg protected def multInt(b: MyInteger): MyNumber = this protected def divInt(b: MyInteger): MyNumber = if (b.isZero) new PosInf else if(b.isInf) new Zero else this protected def powInt(b: MyInteger): MyNumber = this.suc protected def powFrac(b: Fraction): MyNumber = this.suc protected def lessThanInt(b: MyInteger): Boolean = !b.isNeg && !b.isZero protected def biggerThanInt(b: MyInteger): Boolean = b.isNeg && !b.isZero protected def equalsInt(b: MyInteger): Boolean = b.isZero def pre: MyInteger = new Pre(this) def suc: MyInteger = new Suc(this) def neg = this } class PosInf extends MyInteger { val isZero = false val isNeg = false val isInf = true protected def plusInt(b: MyInteger): MyNumber = this protected def minusInt(b: MyInteger): MyNumber = this protected def multInt(b: MyInteger): MyNumber = this protected def divInt(b: MyInteger): MyNumber = this protected def powInt(b: MyInteger): MyNumber = this protected def powFrac(b: Fraction): MyNumber = this protected def lessThanInt(b: MyInteger): Boolean = false protected def biggerThanInt(b: MyInteger): Boolean = true protected def equalsInt(b: MyInteger): Boolean = b.isInf def pre: MyInteger = this def suc: MyInteger = this def neg = this } class Pre(nb: MyInteger) extends MyInteger { val isZero = false val isNeg = true val isInf = false protected def plusInt(b: MyInteger): MyNumber = { def iter(b: MyInteger, accu: MyNumber): MyNumber = { if (b isNeg) this - (b neg) else if (b isZero) accu else iter(b.pre, accu.suc) } iter(b, this) } protected def minusInt(b: MyInteger): MyNumber = { def iter(b: MyInteger, accu: MyNumber): MyNumber = { if (b isNeg) (this + (b neg)) else if (b isZero) accu else iter(b.pre, accu.pre) } iter(b, this) } protected def multInt(b: MyInteger): MyNumber = { (this.neg * b).neg } protected def divInt(b: MyInteger): MyNumber = if (b.isZero) new PosInf else if(b.isInf) new Zero else if (b.isNeg) this.abs / b.abs else (this.abs / b).neg protected def powInt(b: MyInteger): MyNumber = if(b!=new Zero)(this.neg ^ b).neg else (new Zero).suc protected def powFrac(b: Fraction): MyNumber = (new Zero).pre //TODO protected def lessThanInt(b: MyInteger): Boolean = { def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match { case true => !(a isZero) && (b isZero) case false => iter(a.suc, b.suc) } if (!b.isNeg || b.isZero) true else iter(this, b) } protected def biggerThanInt(b: MyInteger): Boolean = { def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match { case true => (a isZero) && !(b isZero) case false => iter(a.suc, b.suc) } if (!b.isNeg || b.isZero) false else iter(this, b) } protected def equalsInt(b: MyInteger): Boolean = !(this < b) && !(this > b) def pre: MyInteger = new Pre(this) def suc: MyInteger = nb def neg = { def iter(nb: MyInteger, accu: MyInteger): MyInteger = { if (nb isZero) accu else iter(nb.suc, accu.suc) } iter(this, new Zero) } } class Suc(nb: MyInteger) extends MyInteger { val isZero = false val isNeg = false val isInf = false protected def plusInt(b: MyInteger): MyNumber = { def iter(b: MyInteger, accu: MyNumber): MyNumber = { if (b isNeg) this - (b neg) else if (b isZero) accu else iter(b.pre, accu.suc) } iter(this, b) } protected def minusInt(b: MyInteger): MyNumber = { def iter(b: MyInteger, accu: MyNumber): MyNumber = { if (b isNeg) this + (b neg) else if (b isZero) accu else iter(b.pre, accu.pre) } iter(b, this) } protected def multInt(b: MyInteger): MyNumber = { def iter(a: MyInteger, b: MyInteger, accu: MyNumber): MyNumber = { if (b.isZero) accu else iter(a, b.pre, accu + a) } if (b.isZero) new Zero else { if (this < b) { if (b.isNeg) iter(b.neg.toInteger, this, new Zero).neg else iter(b, this, new Zero) } else { if (b.isNeg) iter(this, b.neg.toInteger, new Zero).neg else iter(this, b, new Zero) } } } protected def divInt(b: MyInteger): MyNumber = { def iter(a: MyNumber, b: MyNumber, count: MyNumber): MyNumber = { if (a.isZero) count else if (a.isNeg) count.pre else iter(a - b, b, count.suc) } if (b.isZero) new PosInf else if(b.isInf) new Zero else if (b.isNeg) iter(this, b.abs, new Zero).neg else iter(this, b, new Zero) } protected def powInt(b: MyInteger): MyNumber = { def iter(a: MyInteger, b: MyInteger, accu: MyNumber): MyNumber = { if (b.isZero) accu else iter(a, b.pre, accu * a) } if (b.isZero) (new Zero).suc else { if (b.isNeg) new Fraction((new Zero).suc, iter(this, b.neg.toInteger, (new Zero).suc).toInteger) else new Fraction(iter(b, this, (new Zero).suc).toInteger) } } protected def powFrac(b: Fraction): MyNumber = (new Zero).pre //TODO protected def lessThanInt(b: MyInteger): Boolean = { def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match { case true => (a isZero) && !(b isZero) case false => iter(a.pre, b.pre) } if (b.isNeg || b.isZero) false else iter(this, b) } protected def biggerThanInt(b: MyInteger): Boolean = { def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match { case true => !(a isZero) && (b isZero) case false => iter(a.pre, b.pre) } if (b.isNeg || b.isZero) true else iter(this, b) } protected def equalsInt(b: MyInteger): Boolean = !(this < b) && !(this > b) def pre: MyInteger = nb def suc: MyInteger = new Suc(this) def neg = { def iter(nb: MyInteger, accu: MyInteger): MyInteger = { if (nb isZero) accu else iter(nb.pre, accu.pre) } iter(this, new Zero) } } 

अंश वर्ग कुछ आसान है, क्योंकि यह पूरी तरह से MyInteger पर आधारित है:

 class Fraction(x: MyInteger, y: MyInteger) extends MyNumber { def this(x: MyInteger) = this(x, (new Zero).suc) val isNatural: Boolean = false val isNeg: Boolean = (x.isNeg && !y.isNeg) || (!x.isNeg && y.isNeg) val isZero: Boolean = x.isZero val isInf: Boolean = x.isInf || y.isInf def +(b: MyNumber): MyNumber = this plus b.toFraction private def plus(b: Fraction): MyNumber = new Fraction((this.num * b.denum + this.denum * b.num).toInteger, (this.denum * b.denum).toInteger) def -(b: MyNumber): MyNumber = this minus b.toFraction private def minus(b: Fraction): MyNumber = new Fraction((this.num * b.denum - this.denum * b.num).toInteger, (this.denum * b.denum).toInteger) def *(b: MyNumber): MyNumber = this mult b.toFraction private def mult(b: Fraction): MyNumber = new Fraction((this.num * b.num).toInteger, (this.denum * b.denum).toInteger) def /(b: MyNumber): MyNumber = this div b.toFraction private def div(b: Fraction): MyNumber = new Fraction((this.num * b.denum).toInteger, (this.denum * b.num).toInteger) def ^(b: MyNumber): MyNumber = if (!b.isNatural) (new Zero).pre else new Fraction((this.num ^ b.toInteger).toInteger, (this.denum ^ b.toInteger).toInteger) def <(b: MyNumber): Boolean = if (this.num.isNeg) { if (b.num.isNeg) this.neg > b.neg else true } else if (this.isZero) { if (b.isZero || b.num.isNeg) false else true } else { if (b.num.isNeg || b.isZero) false else this.num * b.denum < this.denum * b.num } def >(b: MyNumber): Boolean = if(this.num.isNeg){ if(b.num.isNeg) this.neg < b.neg else false }else if(this.isZero){ if(b.isZero || !b.num.isNeg) false else true }else{ if(b.num.isNeg || b.isZero) true else this.num * b.denum > this.denum * b.num } def ==(b: MyNumber): Boolean = if(!b.isNatural)(this.num == b.num) && (this.denum == b.denum) else this == b.toFraction def neg: MyNumber = new Fraction(num.neg.toInteger, denum) def abs: MyNumber = new Fraction(num.abs.toInteger, denum) def pre: MyInteger = sys.error("Predicat of fraction") def suc: MyInteger = sys.error("Successor of fraction") val num = ((if(this.isNeg)x.abs.neg else x.abs) / (x.abs gcd y.abs)).toInteger val denum = (y.abs / (x.abs gcd y.abs)).toInteger def gcd(b: MyNumber): MyNumber = this.denum gcd (new Zero).suc def mod(b: MyInteger): MyNumber = new Zero override def toString(): String = if(num.isZero) 0.toString() else if(this.isInf) "" else if(denum == (new Zero).suc) num.toString() else num + "/" + denum } 

वह सब है! अब हमारे पास प्राकृतिक और भिन्नात्मक संख्याएं हैं, और सरल ऑपरेशन का एक सेट (आप पर ध्यान दें, देशी कक्षाओं का एक भी उपयोग नहीं है!)

उसी सिद्धांत का उपयोग करके, आप नई दिखाई गई संख्याओं के लिए डेटा संरचना बना सकते हैं:

 abstract class MySet { def add(elem: MyNumber): MySet def delete(elem: MyNumber): MySet def union(set: MySet): MySet def intersec(set: MySet): MySet def contains(elem: MyNumber): Boolean def linearSearch(elem: MyNumber): MySet def mergeSort: MySet def merge: MySet def quickSort: MySet def timSort: MySet def binaryTreeSort: MySet def length: MyNumber def get(pos: MyNumber): MyNumber def take(n: MyNumber): MySet def drop(n: MyNumber): MySet def map(p: MyNumber => MyNumber): MySet def filter(p: MyNumber => Boolean): MySet def flat(p: (MyNumber, MyNumber) => MyNumber): MyNumber 

हां, और बहुत सारी चीजें पुनरावर्ती कार्यों के साथ की जा सकती हैं, यहां तक ​​कि अपना ब्रह्मांड भी बना सकती हैं। "लाठी और वेश्या के साथ।" आपका ध्यान देने के लिए धन्यवाद।