कलमन फ़िल्टर - परिचय

कलामन फ़िल्टर संभवतः विज्ञान और प्रौद्योगिकी के कई क्षेत्रों में उपयोग किया जाने वाला सबसे लोकप्रिय फ़िल्टरिंग एल्गोरिदम है। इसकी सादगी और प्रभावशीलता के कारण, यह जीपीएस-रिसीवर्स, सेंसर रीडिंग के प्रोसेसर, जब नियंत्रण प्रणाली को लागू करता है, आदि में पाया जा सकता है।

इंटरनेट पर (मुख्य रूप से अंग्रेजी में) कलमैन फिल्टर के बारे में बहुत सारे लेख और किताबें हैं, लेकिन इन लेखों में प्रविष्टि के लिए उच्च सीमा है, कई अस्पष्ट स्थान हैं, हालांकि वास्तव में यह एक बहुत ही स्पष्ट और पारदर्शी एल्गोरिथ्म है। मैं सरल भाषा में उसके बारे में बात करने की कोशिश करूंगा, जिसमें धीरे-धीरे जटिलता बढ़ेगी।

इसके लिए क्या है?

किसी भी मापने वाले उपकरण में कुछ त्रुटि होती है, यह बड़ी संख्या में बाहरी और आंतरिक प्रभावों से प्रभावित हो सकता है, जो इस तथ्य की ओर जाता है कि इससे जानकारी शोर है। डेटा जितना अधिक शोर करता है, ऐसी जानकारी को संसाधित करना उतना ही मुश्किल होता है।

फ़िल्टर एक डेटा प्रोसेसिंग एल्गोरिथ्म है जो शोर और अतिरिक्त जानकारी को हटा देता है। कलमन फ़िल्टर में, सिस्टम की प्रकृति, चर के संबंध के बारे में एक प्राथमिक जानकारी निर्धारित करना संभव है, और इसके आधार पर एक अधिक सटीक अनुमान का निर्माण होता है, लेकिन यहां तक ​​कि सबसे सरल मामले में (एक प्राथमिक जानकारी दर्ज किए बिना) यह उत्कृष्ट परिणाम देता है।

सबसे सरल उदाहरण पर विचार करें - मान लें कि हमें टैंक में ईंधन स्तर को नियंत्रित करने की आवश्यकता है। इसके लिए, एक कैपेसिटिव सेंसर टैंक में स्थापित किया गया है, इसे बनाए रखना बहुत आसान है, लेकिन इसकी कुछ कमियां हैं - उदाहरण के लिए, ईंधन भरने पर निर्भरता (ईंधन का ढांकता हुआ निरंतर कई कारकों पर निर्भर करता है, उदाहरण के लिए, तापमान), टैंक में "चीटर" का बड़ा प्रभाव। नतीजतन, इससे प्राप्त जानकारी एक सभ्य आयाम के साथ एक विशिष्ट "देखा" का प्रतिनिधित्व करती है। इस तरह के सेंसर अक्सर भारी खनन उपकरणों पर लगाए जाते हैं (टैंक की मात्रा से भ्रमित न हों):

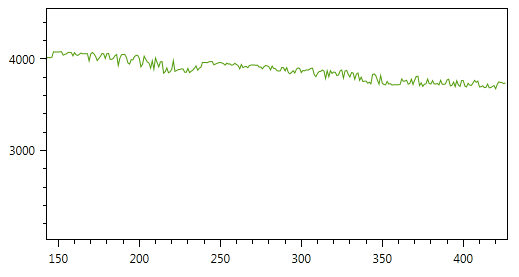
कलमन फ़िल्टर

आइए थोड़ा सा खोदें और एल्गोरिथम से परिचित हों। कलमन फ़िल्टर सिस्टम के एक गतिशील मॉडल (उदाहरण के लिए, गति का भौतिक नियम), प्रसिद्ध नियंत्रण क्रियाओं और कई लगातार मापों का उपयोग करके इष्टतम स्थिति का अनुमान लगाता है। एल्गोरिथ्म में दो दोहराए जाने वाले चरण होते हैं: भविष्यवाणी और समायोजन। सबसे पहले, समय पर अगले क्षण में राज्य की भविष्यवाणी की गणना की जाती है (उनके माप की अशुद्धि को ध्यान में रखते हुए)। दूसरे पर, सेंसर से नई जानकारी अनुमानित मूल्य को सही करती है (इस जानकारी की अशुद्धि और शोर को ध्यान में रखते हुए):



समीकरण मैट्रिक्स रूप में प्रस्तुत किए जाते हैं, यदि आप रैखिक बीजगणित नहीं जानते हैं - यह ठीक है, तो एक चर के साथ मामले के लिए मैट्रिसेस के बिना एक सरलीकृत संस्करण होगा। एकल चर के मामले में, मैटलर स्केलर मान में पतित हो जाते हैं।

पहले नोटेशन पर एक नजर डालते हैं: सबस्क्रिप्ट समय में बिंदु को इंगित करता है: k वर्तमान है, (k-1) पिछले एक है, ऊपरी सूचकांक में शून्य से संकेत मिलता है कि यह एक अनुमानित मध्यवर्ती मूल्य है।

चर विवरण निम्नलिखित छवियों में प्रस्तुत किए गए हैं:





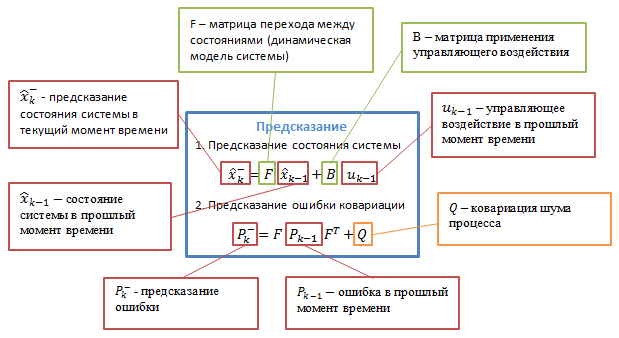
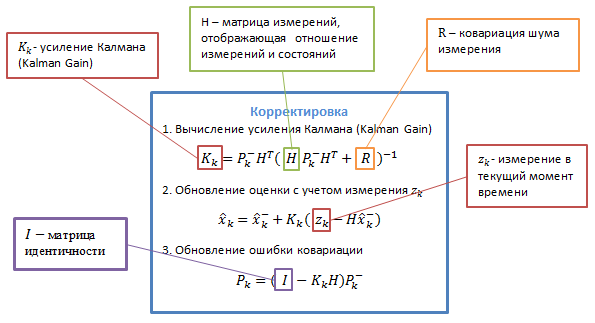
यह लंबे समय तक वर्णन करना संभव है और tediously इन सभी रहस्यमय संक्रमण matrices का मतलब है, लेकिन यह बेहतर है, मेरी राय में, एक वास्तविक उदाहरण का उपयोग करके एक एल्गोरिथ्म का उपयोग करने की कोशिश करना है - ताकि अमूर्त मूल्यों को वास्तविक अर्थ मिल जाए।

हम में परीक्षण करेंगे

आइए हम ईंधन स्तर सेंसर के साथ उदाहरण पर लौटते हैं, क्योंकि सिस्टम की स्थिति को एक चर (टैंक में ईंधन की मात्रा) द्वारा दर्शाया जाता है, मैट्रिसेस सामान्य समीकरणों में गिरावट करते हैं:

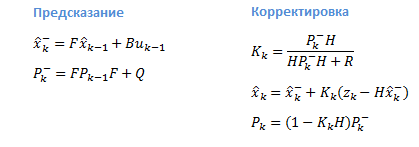
प्रक्रिया मॉडल परिभाषा

फ़िल्टर को लागू करने के लिए, वैरिएबल के मैट्रिक्स / मूल्यों को निर्धारित करना आवश्यक है जो सिस्टम की गतिशीलता और एफ, बी और एच की माप निर्धारित करते हैं:

एफ - ईंधन के मामले में प्रणाली की गतिशीलता का वर्णन करने वाला एक चर - यह नमूना समय (एल्गोरिथम के चरणों के बीच का समय) के लिए निष्क्रिय में ईंधन की खपत का निर्धारण करने वाला एक गुणांक हो सकता है। हालांकि, ईंधन की खपत के अलावा, गैस स्टेशन भी हैं ... इसलिए, सादगी के लिए, हम इस चर को 1 के बराबर लेते हैं (अर्थात, हम इंगित करते हैं कि अनुमानित मूल्य पिछले राज्य के बराबर होगा)।

बी एक चर है जो नियंत्रण कार्रवाई के आवेदन को निर्धारित करता है। यदि हमें इंजन की गति या त्वरक पेडल को निराशाजनक करने की डिग्री के बारे में अतिरिक्त जानकारी थी, तो यह पैरामीटर निर्धारित करेगा कि नमूनाकरण के दौरान ईंधन की खपत कैसे बदल जाएगी। चूंकि हमारे मॉडल में कोई नियंत्रण क्रियाएं नहीं हैं (उनके बारे में कोई जानकारी नहीं है), हम B = 0 लेते हैं।

एच वह मैट्रिक्स है जो माप और सिस्टम की स्थिति के बीच संबंध को परिभाषित करता है, जब तक कि स्पष्टीकरण के बिना हम इस चर को 1 के बराबर भी लेते हैं।

गुणों को चौरसाई करने का निर्धारण

माप उपकरणों को मापने और उनके माप की त्रुटि का निर्धारण करके माप माप को निर्धारित किया जा सकता है।

क्यू - प्रक्रिया के शोर का निर्धारण एक अधिक कठिन कार्य है, क्योंकि प्रक्रिया के विचरण को निर्धारित करना आवश्यक है, जो हमेशा संभव नहीं होता है। किसी भी स्थिति में, इस पैरामीटर को आवश्यक स्तर के निस्पंदन प्रदान करने के लिए चुना जा सकता है।

हम कोड में लागू करते हैं

शेष अस्पष्टता को दूर करने के लिए, हम C # में एक सरल एल्गोरिथ्म लागू करते हैं (मैट्रिसेस और कंट्रोल एक्शन के बिना):

class KalmanFilterSimple1D { public double X0 {get; private set;} // predicted state public double P0 { get; private set; } // predicted covariance public double F { get; private set; } // factor of real value to previous real value public double Q { get; private set; } // measurement noise public double H { get; private set; } // factor of measured value to real value public double R { get; private set; } // environment noise public double State { get; private set; } public double Covariance { get; private set; } public KalmanFilterSimple1D(double q, double r, double f = 1, double h = 1) { Q = q; R = r; F = f; H = h; } public void SetState(double state, double covariance) { State = state; Covariance = covariance; } public void Correct(double data) { //time update - prediction X0 = F*State; P0 = F*Covariance*F + Q; //measurement update - correction var K = H*P0/(H*P0*H + R); State = X0 + K*(data - H*X0); Covariance = (1 - K*H)*P0; } } // ... var fuelData = GetData(); var filtered = new List<double>(); var kalman = new KalmanFilterSimple1D(f: 1, h: 1, q: 2, r: 15); //  F, H, Q  R kalman.SetState(fuelData[0], 0.1); //    State  Covariance foreach(var d in fuelData) { kalman.Correct(d); //   filtered.Add(kalman.State); //    } 

इन मापदंडों के साथ फ़िल्टर करने का परिणाम चित्र में दिखाया गया है (चौरसाई की डिग्री को समायोजित करने के लिए - आप क्यू और आर मापदंडों को बदल सकते हैं):



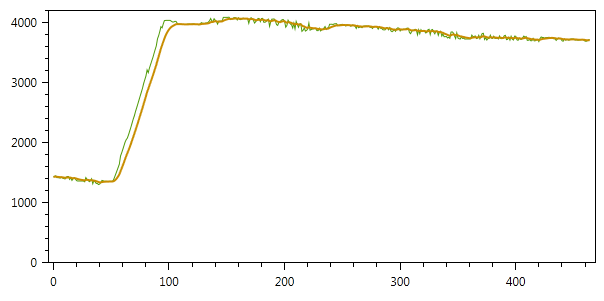
लेख के बाहर, सबसे दिलचस्प बात बनी रही - कई चरों के लिए कलमन फ़िल्टर का अनुप्रयोग, उनके बीच संबंध स्थापित करना और बिना सोचे-समझे चरों के लिए मूल्यों का स्वचालित उत्पादन। मैं समय मिलते ही विषय को जारी रखने का प्रयास करूंगा।

मुझे उम्मीद है कि विवरण बहुत थकाऊ और जटिल नहीं है, अगर आपके पास प्रश्न और स्पष्टीकरण हैं - टिप्पणी में आपका स्वागत है)

UPD: स्रोतों की सूची:
CS373 - एक रोबोट कार की प्रगति - अत्यधिक अनुशंसा
विकिपीडिया (रूसी)
विकिपीडिया (इंग्लैंड)।
हब पर: 1 और 2

अधिक गंभीर स्रोत:
ग्रेग वेल्च, गैरी बिशप, कलमन फ़िल्टर का एक परिचय, 2001
MSGrewal, AP Andrews, “Kalman Filtering - Theory and Practice Using MATLAB,” विली, 2001

UPD2: इस लेख में उदाहरण विशुद्ध रूप से एक डेमो है। फ़िल्टर का मुख्य अनुप्रयोग अधिक जटिल सिस्टम है। उदाहरण के लिए, एक कार के निर्देशांक निर्धारित करने के मामले में, आप जीपीएस निर्देशांक, स्टीयरिंग कोण, इंजन की गति ... लिंक कर सकते हैं और यह सब निर्देशांक की सटीकता को बढ़ाएगा।