स्केन के रास्ते पर: ब्लोफिश के बारे में सरल और स्पष्ट

बग्गी ने कहा, "पगफिश के पेट से बग्गी निकल जाती है। जब खतरा दिखाई देता है, तो वे पानी या हवा से भर जाते हैं, जिससे मछली गुब्बारे की तरह दिखती है
फैला हुआ रीढ़ के साथ। गोलाकार राज्य मछली को लगभग अजेय बनाता है। यदि, हालांकि, एक पर्याप्त बड़े शिकारी ऐसी गेंद को निगलने की कोशिश करता है, तो वह फंस जाती है
एक शिकारी के गले में जो बाद में मर जाता है ”

विकिपीडिया, मुक्त विश्वकोश।

1993 के अंत तक, क्रिप्टोग्राफी की दुनिया में एक बहुत ही अजीब स्थिति पैदा हुई। डेस सममित एन्क्रिप्शन एल्गोरिथ्म, इसकी कमजोर 56-बिट कुंजी के साथ, एक फियास्को, और मौजूदा वाले के करीब था
उस समय, खूफ़ू, REDOC II, IDEA जैसे विकल्प पेटेंट द्वारा संरक्षित थे
और मुफ्त उपयोग के लिए उपलब्ध नहीं है। आरएसए सिक्योरिटी द्वारा उस समय विकसित RC2 और RC4 एल्गोरिदम को भी एक लाइसेंसिंग प्रक्रिया की आवश्यकता थी। और सामान्य तौर पर, सरकारी संगठनों और बड़े निगमों के भीतर क्रिप्टोग्राफी उद्योग रहा है
स्किपजैक जैसे गुप्त एल्गोरिदम के उपयोग की ओर।

एक निश्चित निर्वात उत्पन्न हुआ है। एक एन्क्रिप्शन एल्गोरिथ्म की आवश्यकता थी जो कि डेसिंग डेस की तुलना में अधिक क्रिप्टोग्राफिक था, और साथ ही साथ इसका उपयोग करने के अधिकार पर किसी भी प्रतिबंध के बिना।

और वह दिखाई दिया।

1994 में, कैम्ब्रिज में फास्ट सॉफ्टवेयर एन्क्रिप्शन कार्यशाला में, और बाद में कंप्यूटर साइंस (# 809, 1994) में लेक्चर नोट्स पत्रिका में, ब्रूस श्नेयर ने अपने ब्लॉक सिफर एल्गोरिथ्म को प्रस्तुत किया, जिसे ब्लोफिश नाम दिया गया था।

इस एल्गोरिथ्म की विशिष्ट विशेषताएं डेस की तुलना में क्रिप्टोग्राफिक स्थिरता की एक उच्च डिग्री है (एक चर कुंजी लंबाई के उपयोग के माध्यम से, 448 बिट्स तक), उच्च एन्क्रिप्शन / डिक्रिप्शन गति (प्रतिस्थापन तालिकाओं की पीढ़ी के कारण) और, ज़ाहिर है, किसी भी के लिए इसके मुफ्त उपयोग की संभावना। प्रयोजनों।

संग्रह से 1994 से ब्रूस श्नाइयर का मूल लेख:
ब्लॉक सिफर्स II, ब्रूस श्नेयर (पृष्ठ के नीचे):
एक नई चर-लंबाई कुंजी, 64-बिट ब्लॉक सिफर (ब्लोफिश) का विवरण। 191-204

या पीडीएफ में

परिचय

ब्लोफिश एक 64-बिट ब्लॉक सिफर एल्गोरिथ्म है जिसमें एक चर-लंबाई कुंजी है। इसे 1993 में क्रिप्टोग्राफी और सूचना सुरक्षा ब्रूस श्नाइयर के क्षेत्र में एक प्रसिद्ध विशेषज्ञ द्वारा विकसित किया गया था।

सामान्य स्थिति में, एल्गोरिथ्म में दो चरण होते हैं - प्रमुख विस्तार और स्रोत डेटा का एन्क्रिप्शन / डिक्रिप्शन।



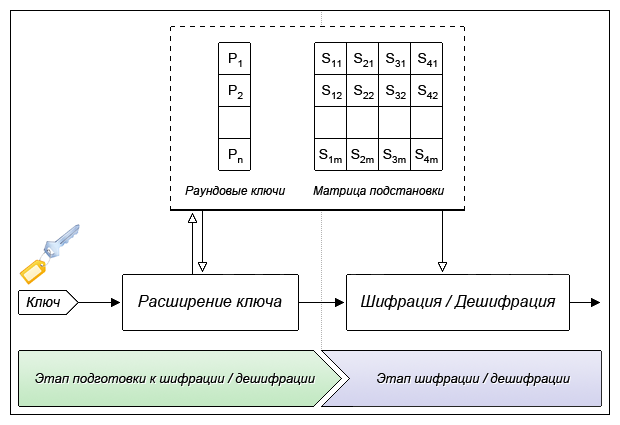
मुख्य विस्तार के चरण में, मूल कुंजी को गोल कुंजी (P) के मैट्रिक्स में परिवर्तित किया जाता है
और एक प्रतिस्थापन मैट्रिक्स (एस, प्रतिस्थापन बॉक्स) (या प्रतिस्थापन), कुल 4168 बाइट्स। सभी संभावना में, यह "विस्तार" (448 बिट्स से 4168 बाइट्स तक) नाम की पसंद बताता है
ब्लोफिश एल्गोरिथ्म।

डेटा एन्क्रिप्शन, साथ ही साथ गोल कुंजी और प्रतिस्थापन के मैट्रिक्स का निर्माण, फिस्टल नेटवर्क के उपयोग के माध्यम से होता है, जिसमें बदले में 16 राउंड होते हैं। इसलिए, कुंजी विस्तार और डेटा एन्क्रिप्शन के चरणों पर विस्तार से विचार करने से पहले, हमें यह तय करने की आवश्यकता है कि उल्लिखित Feistel नेटवर्क क्या है।

प्रक्रिया में, हम C ++ में ब्लोफिश एल्गोरिथ्म के अनुसार एनकोडर के लिए प्रोग्राम कोड लागू करते हैं। उच्च-स्तरीय भाषाओं के लिए तैयार-किए गए कार्यान्वयन (जैसे C / C ++ / Haskell / Perl / ...) पृष्ठ पर उपलब्ध हैं
ब्रूस श्नीयर की साइट पर स्रोत कोड के साथ।

Feistel नेटवर्क

1971 में, आईबीएम कॉरपोरेशन में डेस मानक के "गॉडफादर", हॉर्स्ट फेइस्टेल ने दो उपकरणों का विकास किया, जिन्होंने विभिन्न एन्क्रिप्शन एल्गोरिदम को लागू किया, जिसे बाद में आम नाम "लूसिफ़ेर" कहा गया। इन उपकरणों में से एक में, उन्होंने एक सर्किट का उपयोग किया था जिसे बाद में फिस्टल नेटवर्क कहा जाता था। यह नेटवर्क एक निश्चित बार-बार चलने वाली (दोहराई जाने वाली) संरचना है, जिसे फेइस्टेल सेल कहा जाता है।



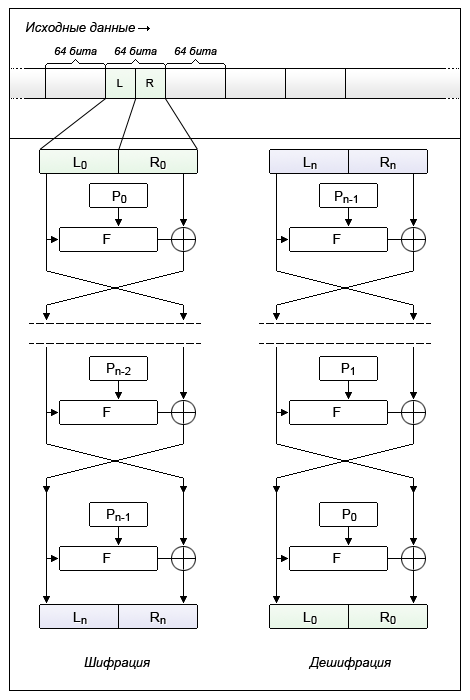
नेटवर्क का सिद्धांत काफी सरल है:

1. स्रोत डेटा को एक निश्चित लंबाई (आमतौर पर दो - 64 बिट्स, 128 बिट्स की शक्ति का एक बहु) के ब्लॉक में विभाजित किया गया है। यदि स्रोत डेटा के ब्लॉक की लंबाई सिफर की लंबाई की लंबाई से कम है, तो ब्लॉक कुछ ज्ञात तरीके से पूरक है।
   
   
2. ब्लॉक को दो समान उप-ब्लॉक में विभाजित किया गया है - "लेफ्ट" एल ₀ और "राइट" आर ₀ ।
   64-बिट क्षमता के मामले में, 32 बिट्स की लंबाई के साथ दो ब्लॉक।
   
   
3. "लेफ्ट सब-ब्लॉक" L _{0 को} पुनरावृति फ़ंक्शन F (L ₀ , P ₀ ) द्वारा संशोधित किया गया है जो कुंजी P ₀ पर निर्भर करता है,
   जिसके बाद इसे "राइट सब-ब्लॉक" R _{0 के} साथ modulo 2 (XOR) जोड़ा जाता है।
   
   
4. जोड़ का परिणाम नए बाएं सब-ब्लॉक L ₁ को सौंपा गया है, जो अगले राउंड के लिए इनपुट डेटा के बाएं आधे हिस्से में हो जाता है, और "बाएँ सब-ब्लॉक" L _{0 को} नए दाएँ सब-ब्लॉक R _{1 में} परिवर्तन किए बिना असाइन किया जाता है, जो दाईं ओर आधा हो जाता है।
   
   
5. यह ऑपरेशन n-1 बार दोहराया जाता है, एक चरण से दूसरे चरण में जाते समय, गोल कुंजियां (P ₀ , P ₁ , P ₂ , आदि) बदल जाती हैं, जहां n उपयोग किए गए एल्गोरिदम के लिए राउंड की संख्या है।

डिक्रिप्शन प्रक्रिया एन्क्रिप्शन प्रक्रिया के समान है सिवाय इसके कि गोल कुंजियां रिवर्स ऑर्डर में उपयोग की जाती हैं।

वापस ब्लोफिश एल्गोरिथ्म के लिए।

सामान्य तौर पर, ब्लोफिश एन्क्रिप्शन एल्गोरिथ्म एक फेइस्टेल नेटवर्क है, लेकिन राउंड कीज़ के निर्माण और उपयोग की कुछ विशेषताओं के साथ (P ₀ , P1 ...)।

शुरुआत करने के लिए, मान लें कि ब्लोफिश एल्गोरिथ्म में पुनरावृति फ़ंक्शन एफ कुछ प्रकार का "ब्लैक बॉक्स" है , जो इनपुट और आउटपुट पर 32-बिट नंबर (DWORD) प्राप्त करता है।

इस मामले में, 32-बिट गोल कुंजियाँ Pn:

1. स्रोत कुंजी से कुछ नियम के अनुसार गणना (448 बिट तक);
2. पुनरावृत्ति फ़ंक्शन एफ के लिए तर्क नहीं हैं;
3. सीधे "बाएं ब्लॉक" के साथ modulo 2 (XOR) जोड़ें।
   इस ऑपरेशन का परिणाम फ़ंक्शन एफ के लिए आने वाली 32-बिट तर्क है ।

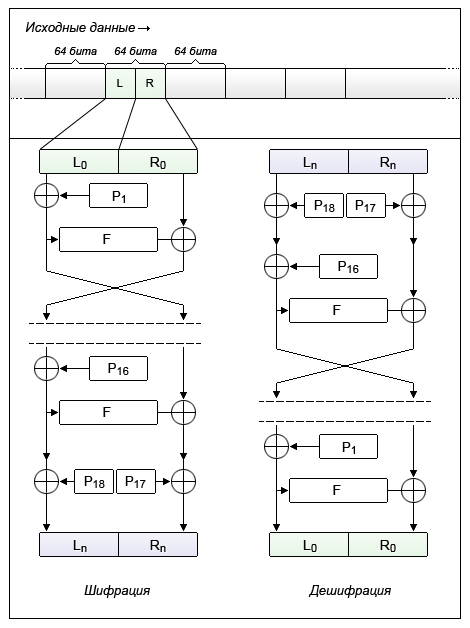
ब्लोफिश एल्गोरिथ्म में, 16 राउंड एन्क्रिप्शन (फेइस्टेल नेटवर्क के अंदर) के दौरान किए जाते हैं, और अंतिम राउंड के बाएं और दाएं आउटपुट ब्लॉक में 17 वीं और 18 वीं कीज को जोड़ा जाता है। राउंड की इस संख्या को चुना गया था, क्योंकि यह एक संभावित कुंजी की लंबाई निर्धारित करता है।

लेकिन यहां चौकस पाठक का सवाल हो सकता है: यदि 18 गोल कुंजियों का उपयोग किया जाता है, जिनमें से प्रत्येक की लंबाई 32 बिट्स है, तो अंत में हमें 576 बिट्स (18 कुंजी × 32 बिट्स) की लंबाई के साथ एक कुंजी मिलती है। ब्लोफिश में स्रोत कुंजी की लंबाई शुरू में 448 बिट्स तक सीमित क्यों है?

इसका उत्तर सरल है - यह सीमित नहीं है। आप 576 बिट तक कुंजियों का उपयोग कर सकते हैं। लेकिन! एल्गोरिथ्म की सुरक्षा और क्रिप्टोग्राफिक स्थिरता के अवलोकन के लिए आवश्यकताओं के आधार पर प्रतिबंध बनाया गया था।

आइए C ++ में ब्लोफिश एल्गोरिथ्म के लिए Feistel नेटवर्क को लागू करें:

void swap(unsigned long *a, unsigned long *b) { unsigned long temp; if (a && b) { temp = *a, *a = *b, *b = temp; } } void blowfish_encrypt_block(blowfish_ctx *ctx, unsigned long *high, unsigned long *low) { int i; for (i = 0; i < 16; i++) { *high ^= ctx->p[i]; *low ^= F(ctx, *high); swap(low, high); } swap(low, high); *low ^= ctx->p[16]; *high ^= ctx->p[17]; } 

मुख्य एक्सटेंशन (इसे उड़ाएं!)

ब्लोफिश एल्गोरिथ्म का प्रारंभिक चरण प्रमुख विस्तार चरण है। इस चरण की प्रक्रिया में, गोल कुंजी Pn और प्रतिस्थापन मैट्रिक्स के मैट्रिक्स का निर्माण किया जाता है - 4 एस-बॉक्स (प्रतिस्थापन बॉक्स) प्रतिस्थापन ब्लॉक, जिनमें से प्रत्येक में 256 32-बिट तत्व होते हैं।



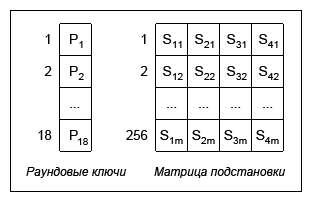
इन मैट्रिसेस के तत्वों को ब्लिफ़िश एल्गोरिथ्म के लिए ऊपर वर्णित फिस्टल नेटवर्क का उपयोग करके एन्क्रिप्ट (गणना) किया गया है। इस प्रकार, ब्लोफिश एल्गोरिथ्म में Feistel नेटवर्क का उपयोग किया जाता है:

• स्रोत डेटा के एन्क्रिप्शन / डिक्रिप्शन के लिए;
• एक गोल कुंजी मैट्रिक्स और एक प्रतिस्थापन मैट्रिक्स (यानी, कुंजी विस्तार) उत्पन्न करने के लिए।

उत्पन्न गोल कुंजी मैट्रिक्स और प्रतिस्थापन मैट्रिक्स बाद में उपयोग किए जाते हैं
एन्क्रिप्शन / डिक्रिप्शन की प्रक्रिया में।

प्रमुख विस्तार प्रक्रिया को संसाधित किया जाता है
18 × 32 (पी ₁ , पी ₂ ...) + 4 × 256 × 32 (एस _1- एस ₄ ) = 33344 बिट्स या 4168 बाइट्स डेटा।

इस मामले में, (18 पीएन) + 4 × 256 (एस _1- एस ₄ )) / 2 = 521 Feistel नेटवर्क के पूर्ण पुनरावृत्ति के लिए किया जाता है।

यह सब बहुत समय लेने वाला ऑपरेशन है, और यही कारण है कि ब्लोफिश एल्गोरिथ्म
अनुशंसित नहीं है, जहां लगातार महत्वपूर्ण परिवर्तनों की आवश्यकता होती है।

हम मुख्य विस्तार एल्गोरिथ्म का वर्णन करते हैं।

1. एक "ईमानदार संख्या" का चयन करता है (या फिर, "मेरी आस्तीन की संख्या कुछ भी नहीं")। यह एक ऐसी संख्या है जिसमें शुरू में कोई दोहराव वाला अनुक्रम नहीं होता है और यह ज्ञात है। यह दिखाने के लिए किया जाता है कि डेवलपर्स को किसी "विले" लक्ष्यों का पीछा किए बिना चुना गया था, उदाहरण के लिए, एल्गोरिथ्म (पिछले दरवाजे) में खामियों को पैदा करने के लिए।
   
   ब्लोफिश आमतौर पर पीआई नंबर का उपयोग ऐसे ईमानदार नंबर के रूप में करता है। हम पीआई नंबर के मूल्य के हेक्साडेसिमल प्रतिनिधित्व की गणना नहीं करेंगे, लेकिन हम पीआई नंबर के लिए मंटिसा के 8366 हेक्साडेसिमल अंकों के लिए एक तैयार समाधान का उपयोग करेंगे।
   
   
2. पीआई संख्या के मंटिसा के मूल्य को गोल कुंजी (FIXED_P) और प्रतिस्थापन मैट्रिक्स (FIXED_S) के मैट्रिक्स में भरने के लिए उपयोग किया जाता है:
   
   

    typedef struct _blowfish_ctx { unsigned long p[18]; unsigned long sbox[4][256]; } blowfish_ctx; const unsigned int FIXED_S[4][256] = { { 0xD1310BA6, 0x98DFB5AC, 0x2FFD72DB, 0xD01ADFB7, 0xB8E1AFED, 0x6A267E96, 0xBA7C9045, 0xF12C7F99, 0x24A19947, 0xB3916CF7, 0x0801F2E2, 0x858EFC16, 0x636920D8, 0x71574E69, 0xA458FEA3, 0xF4933D7E, 0x0D95748F, 0x728EB658, 0x718BCD58, 0x82154AEE, 0x7B54A41D, 0xC25A59B5, 0x9C30D539, 0x2AF26013, ....        .... 0xB74E6132, 0xCE77E25B, 0x578FDFE3, 0x3AC372E6 } }; const unsigned long FIXED_P[] = { 0x243F6A88, 0x85A308D3, 0x13198A2E, 0x03707344, 0xA4093822, 0x299F31D0, 0x082EFA98, 0xEC4E6C89, 0x452821E6, 0x38D01377, 0xBE5466CF, 0x34E90C6C, 0xC0AC29B7, 0xC97C50DD, 0x3F84D5B5, 0xB5470917, 0x9216D5D9, 0x8979FB1B }; 

   
   
   
3. प्रत्येक गोल कुंजी Pn (P ₁ , P ₂ ...) का मान मूल कुंजी K के संगत तत्वों के साथ modulo 2 (XOR) जोड़ा जाता है। उदाहरण के लिए, गोल कुंजी P ₁ का XOR
   मूल कुंजी K के पहले 32 बिट्स के साथ, P ₂ मूल कुंजी K के दूसरे 32 बिट्स के साथ और इसी तरह। यदि मूल कुंजी K सभी गोल कुंजी (576 बिट्स) की लंबाई से छोटी है, तो यह स्वयं को समेटती है
   आपके साथ: केके, केकेके और इतने पर।
   
   

    for(i = 0, k = 0; i < 18; i++) { for(j = 0, long_key = 0; j < 4; j++, k++) { long_key = (long_key << 8) | key[k % key_len]; } ctx->p[i] ^= long_key; } 

   
   
   
4. अगला, हमें गोल कुंजी के मैट्रिक्स और प्रतिस्थापन मैट्रिक्स के तत्वों (नए मूल्यों की गणना) को एन्क्रिप्ट करने की आवश्यकता है। ऐसा करने के लिए, हम ब्लिफ़िश के लिए Feistel नेटवर्क एल्गोरिथ्म का उपयोग करेंगे जो हमने लागू किया है।
   
   
   1. वर्तमान दौर की चाबियाँ पी _1- पी ₁₈ और प्रतिस्थापन मैट्रिस एस ₁ एस ₄ (जहां बिल्कुल प्रतिस्थापन मैट्रिस नीचे वर्णित किया जाएगा) का उपयोग करके, हम 64-बिट शून्य अनुक्रम को एन्क्रिप्ट करते हैं: 0x00000000 0x00000000, और पी ₁ और पी ₂ में परिणाम लिखें ।
      
      
   2. पी ₁ और पी ₂ को गोल कुंजी और प्रतिस्थापन मैट्रिसेस के संशोधित मूल्यों के साथ एन्क्रिप्ट किया गया है, परिणाम क्रमशः पी ₃ और पी ₄ में लिखा गया है।
      
      
   3. एन्क्रिप्शन तब तक जारी रहता है जब तक कि सभी गोल कुंजियाँ P 1PP ₁₈ और प्रतिस्थापन मैट्रीस S ₁ –S _{4 के} तत्व बदल न जाएँ।
      
      यानी अंततः, हमें (18 Pn + 4 × 256 (S ₁ –S ₄ )) / 2 = 521 पुनरावृत्तियों के लिए ब्लोफ़िश एल्गोरिथ्म के Feistel नेटवर्क गणना का परिणाम प्राप्त करने की आवश्यकता है। हमने 2 से विभाजित किया है, क्योंकि प्रत्येक पुनरावृत्ति के लिए हम तुरंत गोल कुंजियों के मैट्रिक्स या क्रमपरिवर्तन के मैट्रिक्स के तत्वों के लिए दो नए मूल्यों की गणना करते हैं।
   
   
   

    for (i = 0, k = 0, l = 0; i < 18; i++) { blowfish_encrypt_block(ctx, (unsigned long*)&k, (unsigned long*)&l); ctx->p[i] = k; ctx->p[++i] = l; } for (i = 0; i < 4; i++) { for (j = 0; j < 256; j++) { blowfish_encrypt_block(ctx, (unsigned long*)&k, (unsigned long*)&l); ctx->sbox[i][j] = k; ctx->sbox[i][++j] = l; } } 

   
   

इस बिंदु पर, ब्लोफिश एल्गोरिथ्म की तैयारी का चरण - प्रमुख विस्तार - पूरा हो गया है। लेकिन इससे पहले कि हम एन्क्रिप्शन / डिक्रिप्शन चरण को देखें, चलो अभी भी हमारे "ब्लैक बॉक्स" को खोलें - फ़ंक्शन एफ, ब्लोफ़िश एल्गोरिथ्म के लिए Feistel नेटवर्क के पुनरावृत्तियों के भीतर प्रत्येक दौर पर निष्पादित।

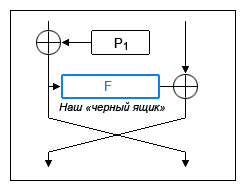
Iteration (राउंड) फ़ंक्शन

गोल या पुनरावृति फ़ंक्शन (चूंकि इसका उपयोग संपूर्ण फिस्टल नेटवर्क के लिए सामान्य है) बहुत सरल है और क्रमचय मैट्रिक्स पर केवल कुछ तार्किक संचालन का उपयोग करता है। प्रारंभ में, लूसिफ़ेर को विकसित करते समय, होर्स्ट फेइस्टेल ने एक इलेक्ट्रॉनिक इकाई के उपयोग को क्रमपरिवर्तन के मैट्रिक्स के लिए एक सरल रैखिक सर्किट के साथ ग्रहण किया।



तो:

1. एक आने वाले 32-बिट ब्लॉक को चार 8-बिट ब्लॉक में विभाजित किया गया है, चलो उन्हें एक्स ₁ , एक्स ₂ , एक्स ₃ , एक्स _{4 कहते हैं}
   (ऊपर चित्र देखें)।
   
   
2. जिनमें से प्रत्येक प्रतिस्थापन तालिका S ₁ -S ₄ की सरणी का एक सूचकांक है।
3. S ₁ [X ₁ ] और S ₂ [X ₂ ] के मान को modulo 2 ³² जोड़ा जाता है, फिर परिणाम जोड़ा जाता है
   modulo 2 (XOR) S ₃ [X ₃ ] के साथ और अंत में S ₄ [X ₄ ] को फिर से modulo 2 ^{32 में जोड़ें} ।
4. गणना का परिणाम एफ (एक्स ₁ -X ₄ ) फ़ंक्शन का मूल्य होगा।

समारोह सूत्र:


सब कुछ बेहद सरल है। फ़ंक्शन S ₁ –S ₄ प्रतिस्थापन मैट्रिसेस का उपयोग करता है रैखिक रूप से प्रतिस्थापन मैट्रिक्स से आने वाले 32 बिट डेटा को एक मूल्य में परिवर्तित करता है। और अर्थ अपने आप
मेट्रिसेस में, प्रतिस्थापन की गणना उस महत्वपूर्ण विस्तार चरण में की जाती है, जिसकी हमने पहले जांच की थी।

C ++ में एक फ़ंक्शन का कार्यान्वयन:

 unsigned long F(blowfish_ctx *ctx, unsigned long x) { return ((ctx->sbox[0][(x >> 24) & 0xFF] + ctx->sbox[1][(x >> 16) & 0xFF]) ^ ctx->sbox[2][(x >> 8) & 0xFF]) + ctx->sbox[3][(x) & 0xFF]; } 

और अब चलो स्रोत डेटा को एन्क्रिप्ट करने की प्रक्रिया को आगे बढ़ाते हैं।

स्रोत डेटा का एन्क्रिप्शन / डिक्रिप्शन

आश्चर्य! वास्तव में, हमने पहले ही स्रोत डेटा के लिए एन्क्रिप्शन और डिक्रिप्शन एल्गोरिथम पर विचार किया है। बात यह है कि, जैसा कि हमने बहुत शुरुआत में देखा था, डेटा एन्क्रिप्शन / डिक्रिप्शन, और राउंड कीज़ की उपरोक्त मैट्रिक्स और एक प्रतिस्थापन मैट्रिक्स का निर्माण, ब्लिफ़िश एल्गोरिथ्म के लिए माना गया Feistel नेटवर्क का उपयोग करके होता है।

यानी हमारे सॉफ्टवेयर कार्यान्वयन में, स्रोत डेटा के एन्क्रिप्शन की पूरी प्रक्रिया को कुंजी विस्तार के चरण में एन्क्रिप्शन प्रक्रिया के साथ सादृश्य द्वारा बनाया गया है। यानी स्रोत डेटा के प्रत्येक 64 बिट पर ब्लोफ़िश_एन्क्रिप्ट_ब्लॉक फ़ंक्शन (फिस्टल नेटवर्क का कार्यान्वयन) के एक पुनरावृत्त निष्पादन का प्रतिनिधित्व करता है। गोल कुंजियाँ P (P ₁ , P ₂ , hellip) और प्रतिस्थापन matrices S ₁ –S ₄ क्रमशः फिस्टल नेटवर्क और इस नेटवर्क के अंदर फ़ंक्शन F के लिए इनपुट पैरामीटर हैं।



नतीजतन, अगर हम ब्लोफ़िश एल्गोरिथ्म में एन्क्रिप्शन या डिक्रिप्शन एल्गोरिथ्म का सारांश देते हैं,
तब हमें निम्न चरण मिलते हैं:

1. हम Feistel नेटवर्क के गोल कुंजियों के लिए 18 तत्वों की एक सरणी का चयन करते हैं और प्रत्येक 256 तत्वों के 4 प्रतिस्थापन मैट्रिसेस।
   
   
2. हम पीआई संख्या के मंटिसा मूल्य के साथ चयनित सरणी को भरते हैं।
   
   
3. एक पुनरावृत्त XOR बनाएं: Pi = Pi XOR Ki (जहां पाई गोल कुंजी है और Ki स्रोत स्रोत है)।
   
   
4. हम फिस्टल नेटवर्क का उपयोग करके गोल कुंजी और प्रतिस्थापन मैट्रिसेस को एन्क्रिप्ट करते हैं (नेटवर्क के भीतर फ़ंक्शन के लिए इनपुट मैट्रिक्स के रूप में प्रतिस्थापन मैट्रिक्स का उपयोग किया जाता है; नेटवर्क के भीतर गोल कुंजी को गोल कुंजी मैट्रिक्स से लिया जाता है)।
   
   
5. हम 64-बिट स्रोत डेटा ब्लॉक को Feistel नेटवर्क का उपयोग करके एन्क्रिप्ट / डिक्रिप्ट करते हैं।
   
   

सब कुछ सरल है।

सारांश

प्रिय पाठकों। सरल शब्दों में जटिल चीजों का वर्णन करने में सक्षम होना बहुत मुश्किल है।

इससे पहले कि मैं यह पाठ लिखना शुरू करूँ, मैंने खुद को डेवलपर के स्थान पर रखने की कोशिश की,
जो चर्चा की गई ब्लोफिश एल्गोरिथ्म का अध्ययन करने की कोशिश करना चाहता है।

इसलिए, मैंने नेटवर्क पर एक दस्तावेज खोजने के लिए निर्धारित किया है जो इस एल्गोरिथ्म को इसकी समझ के लिए पर्याप्त पूर्णता के साथ वर्णन करता है। नतीजतन, निश्चित रूप से मैं विकिपीडिया पृष्ठों, और मंचों, और यहां तक ​​कि अलग-अलग अवधि के कागजात के लिए मिला। लेकिन वहाँ प्रस्तुत विवरण को पढ़ने से अक्सर उत्तर की तुलना में अधिक प्रश्न पैदा होते हैं।

यह सब मुझे इस राय में पुष्टि करता है कि एक सरल और एक ही समय में उदाहरणों के साथ विस्तृत विवरण उपयोगी और मांग में होगा। इसलिए, अपने हिस्से के लिए, मैंने कोशिश की, जहां तक ​​संभव हो, "अलमारियों पर सब कुछ डाल दिया।" लेकिन मैंने इसे कितनी अच्छी तरह जज किया - आपको जज किया।

आपका धन्यवाद
तुम्हारा, अटल बिहारी

ps इसे जारी रखने की योजना है ...