डेटा संपीड़न के लिए रेडिक्स ट्री संरचना

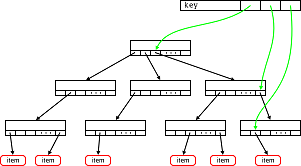
यह विषय व्यावहारिक उदाहरण पर रेडिक्स ट्री के उपयोग के बारे में बताता है। एक मूलांक वृक्ष या अवशिष्ट वृक्ष एक डेटा संरचना है जो पत्ती के नोड में मूल्यों के भंडारण के सिद्धांत पर बनाई गई है। मध्यवर्ती नोड्स परिमित मूल्य का एक तत्व हैं। यह संख्याओं के लिए थोड़ा हो सकता है, तार के लिए एक चरित्र, या संख्या के लिए एक अंक, जैसा कि नीचे दिए गए उदाहरण में है। रेडिक्स ट्री का उपयोग करते हुए उपरोक्त संपीड़न एल्गोरिदम का उपयोग एक वास्तविक एम्बेडेड सिस्टम में टेलीफोन फ़ायरवॉल मापदंडों को संग्रहीत करने के लिए किया जाता है।

संदर्भ की शर्तें

तो स्रोत डेटा।
मान लीजिए हमारे पास एक फोन बुक है, या अधिक बस एक संपर्क सूची है। प्रत्येक संपर्क के साथ
संबंधित विशेषताओं का सेट। "टेलीफोन फ़ायरवॉल" कार्यक्रम के लिए, ये बूलियन विशेषता हो सकते हैं:
आउटगोइंग / इनकमिंग कॉल, वर्किंग / नॉन वर्किंग आवर्स के दौरान काम करना, अनुमति / ब्लॉक या ऑटो का जवाब देना
जब बुला रहा है। कार्य काउंटरपॉइंट की सूची और उनकी विशेषताओं को संपीड़ित रूप में टेलीफोन मेमोरी में संग्रहीत करना है। सीमित उपलब्ध स्मृति की स्थितियों में।

तो, एक अधिक विस्तृत तकनीकी कार्य इस तरह दिखता है:
- प्रत्येक नंबर के लिए नियमों के एक सेट के साथ एक .INI फ़ाइल है। नियम में एक फ़ोन नंबर होता है।
और वास्तविक बूलियन गुण इस पर लागू होते हैं। कमरे अद्वितीय हैं ।
उदाहरण .INI फ़ाइल, जहाँ 12345 फ़ोन नंबर है:
[नियम]
R0000 = 12345,0,0,0,0,0,0,0,0,0,0,0,0
R0001 = 123764465,0,0,0,0,0,1,0,1,0,0,0
...
R0765 = ...

- नियम का आंतरिक प्रतिनिधित्व:

class NumberEntry
{
string number ;
bool attCalledNumber ;
bool attCallingNumber ;
bool attInboundCall ;
bool attOutboundCall ;
bool attWorkingHours ;
bool attNonWorkingHours ;
bool attBlocked ;
bool attAllowed ;
bool attPrefix ;
bool attAutoAnswer ;
};

* This source code was highlighted with Source Code Highlighter .

- नियमों के मौजूदा सेट के लिए, आपको एक मध्यवर्ती विस्तारित ग्राफ़ बनाना चाहिए।
एक ग्राफ में, प्रत्येक नोड को पत्ती के रूप में चिह्नित किया जा सकता है। उदाहरण के लिए, हाइपोपिटेटिक संख्याओं के इस सेट को लें:
012345
012,346
01234567 #
54,647
5463
54,638

एक मध्यवर्ती ग्राफ बनाया जाना चाहिए:

चित्रा 1. ToR से एक विस्तारित (संकुचित नहीं) ग्राफ।

- उन्नत ग्राफ निम्नलिखित नियमों के अनुसार बनाया गया है:
सूची में प्रत्येक संख्या का अंतिम अंक एक पत्ती नोड इंगित करता है। संख्या के साथ जुड़े गुण केवल पत्ती नोड पर लागू होते हैं। एक ग्राफ में, किसी भी नोड को पत्ती के रूप में चिह्नित किया जा सकता है। ऊपर के उदाहरण के लिए, संख्या ०१२३४ ५ में संख्या ५ पत्ती इकाई का प्रतिनिधित्व करती है, हालाँकि यह संख्या ०१२३४ ६ 0 # # का भी हिस्सा है

- सभी संख्याओं को मध्यवर्ती कॉलम (विस्तारित) में जोड़ दिए जाने के बाद, इसे संपीड़ित किया जाना चाहिए। ताकि इंटरमीडिएट ग्राफ के प्रत्येक नोड
(उदाहरण के लिए 0xxx5xxx #), कॉम्पैक्ट नोड्स के अनुक्रम द्वारा प्रतिस्थापित किया जाता है (कॉम्पैक्ट नोड्स, 'x' के बिना)।

विस्तारित और कॉम्पैक्ट ग्राफ के नोड्स निम्नलिखित संरचनाओं द्वारा दर्शाए गए हैं:

#pragma pack(push, 1) // 1 MS C++
#define K_MAX_EXPANDED_NODES 12 // . 0-9, * #
struct SG_Y_DigitElement // , 4
{
UINT digit : 4; // 0-9 . '*' 0xA, '#' 0xB. 12 , 4
UINT nextNodeOffset : 13; // ,
BOOL leafNode : 1; // ?

BOOL attCalledNumber : 1; // .
BOOL attCallingNumber : 1;
BOOL attInboundCall : 1;
BOOL attOutboundCall : 1;
BOOL attWorkingHours : 1;
BOOL attNonWorkingHours : 1;
BOOL attBlocked : 1;
BOOL attAllowed : 1;
BOOL attPrefix : 1;
BOOL attAutoAnswer : 1;
BOOL attReserved1 : 1;
BOOL attReserved2 : 1;
BOOL attReserved3 : 1;
BOOL attReserved4 : 1;
}

typedef SG_Y_DigitElement SG_Y_ExpandedNode[K_MAX_EXPANDED_NODES];

struct SG_Y_CompactNode // 5 . +
{
UINT8 nodeLen : 4;
UINT8 reserved : 4;
/* */
SG_Y_DigitElement digits;
} ;
#pragma pack(pop)

* This source code was highlighted with Source Code Highlighter .

- विस्तारित ग्राफ के आधार पर, जिसे SG_Y_ExpandedNode प्रकार के तत्वों की एक सरणी द्वारा दर्शाया गया है, SG_Y_CompactNode प्रकार के नोड्स के साथ एक कॉम्पैक्ट ग्राफ़ बनाया गया है। इस प्रकार, डेटा SG_Y_ExpandedNode से 'x' के रूप में निर्दिष्ट खाली तत्वों को हटाकर संकुचित किया जाता है। ऊपर दिए गए उदाहरण से विस्तारित ग्राफ के लिए, संपीड़न के बाद कॉम्पैक्ट ग्राफ इस तरह दिखाई देगा (हरा कॉम्पैक्ट नोड में अंकों की संख्या को इंगित करता है, SG_Y_CompactNode संरचना का नोडलेन क्षेत्र):

चित्रा 2. टीके से संकुचित ग्राफ।

- यह ध्यान दिया जाना चाहिए कि दोनों रेखांकन में नोड्स (SG_Y_DigitElement में nextNodeOffset फ़ील्ड) इंगित करते हैं, ग्राफ़ के पहले बाइट के सापेक्ष एक सूचकांक का प्रतिनिधित्व करते हैं। दोनों रेखांकन सरणियों द्वारा दर्शाए गए हैं।

- टो को संक्षेप में प्रस्तुत करने के लिए:

• फोन नंबर के लिए फ़ायरवॉल नियमों के साथ एक .INI फ़ाइल प्राप्त होती है।
• संख्याओं की सूची में नियमों को पढ़ें
• हम सूची के आधार पर एक मध्यवर्ती विस्तारित ग्राफ बनाते हैं। जहां ग्राफ के लीफ नोड में संख्या से संबंधित विशेषताएँ होती हैं।
• हम विस्तारित से खाली तत्वों को हटाकर एक संकुचित ग्राफ बनाते हैं

एक मध्यवर्ती ग्राफ का निर्माण

एल्गोरिथ्म का पहला चरण तुच्छ है। हम मानते हैं कि नियमों को पढ़ा और सूची में जोड़ा गया है। हमारे पास सूची में संख्याओं का एक समूह है, जो ग्राफ जनरेटर के लिए इनपुट है। यहां और संलग्न स्रोतों में, निर्माण और संपीड़न एल्गोरिदम को लागू करने वाले वर्ग को दर्शाने के लिए ग्राफ जनरेटर (ग्राफगेंसर) शब्द का उपयोग किया जाता है।

हम एक मध्यवर्ती विस्तारित ग्राफ (विस्तारित) के निर्माण के लिए सीधे आगे बढ़ते हैं।
चित्रा 1 पर फिर से ध्यान दें। इस मध्यवर्ती ग्राफ को रेडिक्स ट्री (या रूसी एनालॉग अवशेषों का एक पेड़ है) के सिद्धांत पर निर्मित एक द्विआधारी वृक्ष के रूप में दर्शाया जा सकता है। आइए इस डेटा संरचना पर करीब से नज़र डालें।

रेडिक्स ट्री में एक तत्व जोड़ना इस प्रकार है:
- जोड़े गए मूल्य का प्रत्येक-वें बिट लिया जाता है।
- तत्व को वर्तमान बिट के आधार पर, पेड़ के नीचे धकेल दिया जाता है। यदि i-th बिट 0 है, तो बाएं जाएं, अन्यथा दाएं।
और इसलिए जब तक मूल्य के सभी महत्वपूर्ण बिट्स संसाधित नहीं होते हैं।
- परिणामस्वरूप, मूलांक ट्री लीफ नोड स्वयं मूल्य को निरूपित करेगा। इस प्रकार, रूट से लीफ नोड तक,
हमें मूल्य के सभी बिट्स मिलते हैं। दृष्टिकोण का एक चित्रण यहाँ पाया जा सकता है । रूसी विकि का अभी तक कोई रेडिक्स ट्री वर्णन नहीं है।

उदाहरण के लिए, तीन नंबर लें: 0123, 01234, 123 । फिर पहले पुनरावृत्ति पर, पेड़ को ऊपर से नीचे तक बनाया जाएगा, जिससे 4 नोड्स (0,1,2,3-पत्ती) बनेंगे। दूसरे पुनरावृत्ति में, संख्या 01234 जोड़ते समय, हम 0, 1, 2 और 3 तत्वों को जोड़ते समय उसी पथ का अनुसरण करेंगे, क्योंकि इन संख्याओं के लिए नोड्स पहले ही बनाए जा चुके हैं। लेकिन अंतिम तत्व को जोड़ते समय, मान 3 के साथ नोड में होने पर, हम एक नया पत्ता नोड बनाते हैं 4. और तीसरे पुनरावृत्ति में, संख्या 123 जोड़कर, दाईं ओर होता है।

अगर हम परिणामस्वरूप पेड़ को एक ग्राफ के रूप में दर्शाते हैं, जहाँ दाईं ओर नोड "भाई" है और बाईं ओर नोड "बेटा" है, हमें मिलता है

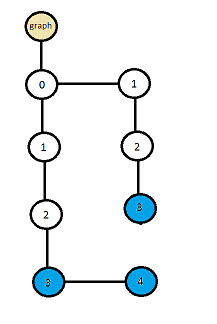चित्रा 3. ग्राफ संबंध

हम अपने विस्तारित ग्राफ के लिए मूलांक ट्री में जोड़ने के लिए एल्गोरिथ्म लागू करते हैं। ग्राफ नोड को 12 संभावित मानों (0-9 * #) के एक सरणी द्वारा दर्शाया गया है। यही है, हम नोड के मान को जांचने और सेट करने के लिए विस्तारित नोड [अंक] मैपिंग का उपयोग करते हैं।
नीचे दिए गए चित्र में, ExpandGraph को विस्तारित नोड नोड्स की एक सरणी के रूप में दर्शाया गया है। '-' एक खाली तत्व को इंगित करता है, नीला तत्व - एक पत्ती नोड को इंगित करता है। मुझे आपको याद दिलाना है कि हमारी समस्या में लीफ नोड में संख्या की विशेषताएं हैं।


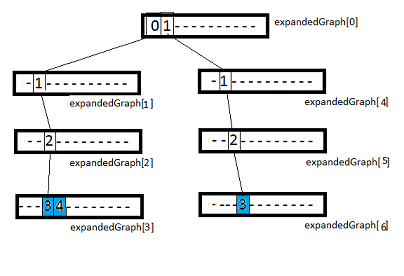चित्रा 4. विस्तारित (असम्पीडित) ग्राफ

मुझे लगता है कि रेडिक्स ट्री का उपयोग करने का विचार पहले से ही स्पष्ट हो रहा है और तस्वीर से यह स्पष्ट है कि खाली तत्वों को हटाकर संपीड़न किया जा सकता है।

संपीड़न। एक कॉम्पैक्ट ग्राफ का निर्माण।

संपीड़न एल्गोरिथ्म अपेक्षाकृत सरल है, और इसे दो वाक्यों में वर्णित किया जा सकता है। हमारे पास एक विस्तारित ग्राफ विस्तारित है, जो विस्तार की एक सरणी के रूप में प्रस्तुत किया गया है।
- हम विस्तारित गैग [i] नोड से गैर-खाली तत्व (संख्या) लेते हैं। हम उन्हें एक संपीड़ित ग्राफ में स्थानांतरित करते हैं, जिसे SG_Y_CompactNode से एक सरणी द्वारा दर्शाया गया है। हम कॉम्पैक्ट इकाई की लंबाई को गैर-रिक्त तत्वों की संख्या के रूप में सेट करते हैं।
- हम प्रत्येक बच्चे के नोड के लिए संपीड़न प्रक्रिया लागू करते हैं। हम कॉम्पैक्टग्राफ की शुरुआत से संबंधित बाल तत्वों के संदर्भ बदलते हैं।

संपीड़न एल्गोरिदम पुनरावर्ती है। हम नोड से गैर-रिक्त तत्वों का चयन करते हैं, और नोड की लंबाई निर्धारित करते हुए, उन्हें एक संपीड़ित ग्राफ में क्रमिक रूप से बाहर करते हैं। इस प्रकार विस्तारित दृश्य नोड से
"01 -----------", हमें एक कॉम्पैक्ट नोड मिलता है '[2] 01', जहां [2] नोड की लंबाई है।
हम पुनरावर्ती रूप से बच्चे के तत्वों '0' और '1' के लिए प्रक्रिया कहते हैं। फिर हम '0' और '1' को संकुचित ग्राफ की शुरुआत के सापेक्ष बच्चों के साथ जोड़ते हैं।


चित्रा 5. परिणाम एक संकुचित ग्राफ है।

निष्कर्ष।

- एल्गोरिथ्म का उपयोग फोन नंबर को कंप्रेस और स्टोर करने के लिए इष्टतम है। मोबाइल ऑपरेटरों , देश या शहर के कोड जैसे उपसर्ग, आपको ग्राफ़ के रूट नोड में इन समान कोडों को संग्रहीत करने की अनुमति देते हैं। कार्यान्वयन का उपयोग सीधे एक बड़ी दूरसंचार कंपनी के सॉफ़्टवेयर में किया जाता है।
हालाँकि, इसका उपयोग किसी भी डेटा अनुक्रम के लिए किया जा सकता है। उदाहरण के लिए, केस-संवेदी लैटिन कैरेक्टर डेटा को स्टोर करने के लिए, ग्राफ नोड के आकार को 26 तत्वों तक बढ़ाने की आवश्यकता है। तदनुसार, अंक क्षेत्र के तहत, 5 बिट्स का चयन करें।
यदि विशेषताओं की आवश्यकता नहीं है, तो SG_Y_DigitElement का आकार 2 बाइट तक कम किया जा सकता है। उदाहरण के लिए, एक चरित्र मान के लिए 5 बिट, अगले नोड के लिए एक पॉइंटर के लिए 10 बिट और शीट मार्कर के लिए 1 बिट।
जाहिर है, पता करने योग्य प्रविष्टियों की संख्या पर सीमा अगले नोडऑफसेट क्षेत्र द्वारा सीमित है। हमारे उदाहरण में, 13 बिट्स 8192 रिकॉर्ड को संबोधित करने के लिए पर्याप्त है।

यहाँ एल्गोरिथ्म का कार्यान्वयन है