त्रि-आयामी कार्यों के ग्रिड रेखांकन और उन्हें अलग करना

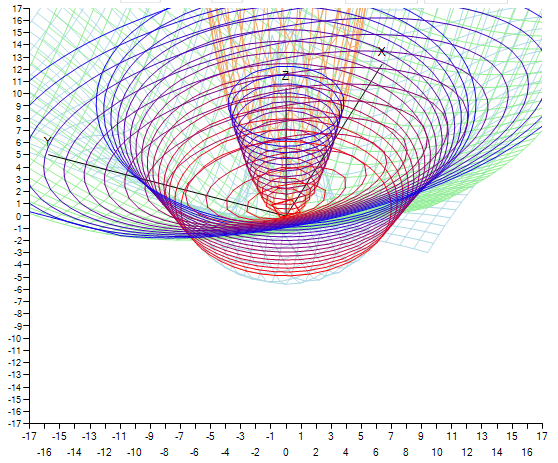
यह आलेख एक प्रकार का "व्यावहारिक मार्गदर्शिका" है, जो कि फॉर्म z = f (x, y) के कार्यों के बहुत ही रोचक तीन आयामी रेखांकन के निर्माण के लिए है, उदाहरण के लिए C # में।

हम चार्ट घटक में आकर्षित करेंगे, निश्चित रूप से, आप किसी भी कैनवास जैसे तत्व का उपयोग कर सकते हैं। बड़ी संख्या में अंकों के साथ, ड्राइंग में देरी देखी जाएगी, लेकिन इस घटक का उपयोग करना आसान है और यह प्रदर्शन के लिए काफी उपयुक्त होगा।

एक चार्ट का निर्माण

ऐसा करने के लिए, हमें एक ग्रिड या फ़ील्ड की आवश्यकता होती है, जिसमें से प्रत्येक नोड में x, y निर्देशांक होंगे और मान z होगा। यह ग्रिड किसी भी तरह से भरा जा सकता है, क्योंकि हम फ़ंक्शन को प्लॉट कर रहे हैं, हम इसे इस फ़ंक्शन (z = f (x, y)) के मूल्यों से भर देंगे। X या y के दो लगातार मूल्यों के बीच का चरण एक के बराबर चुना जाता है, एक सरल और अधिक दृश्य प्रदर्शन के लिए, ग्रिड आयाम N x N है। ग्रिड नोड्स पर मान एक बार विचार करने के लिए पर्याप्त हैं। त्रि-आयामी निर्देशांक को दो-आयामी में बदलने और ग्राफ़ को घुमाने के लिए, हम रोटेशन मैट्रिक्स और यूलर कोण का उपयोग करेंगे।

हम क्रमशः ए, बी, और सी के कोणों द्वारा कोण α, γ, और We को निरूपित करते हैं, और हम उनके मानों को डिग्री में उपयोग करेंगे। हम गुणांक के माध्यम से मैट्रिक्स लिखते हैं:

    |  l1, l2, l3 |	
  म = |  एम 1, एम 2, एम 3 |
    |  एन 1, एन 2, एन 3 |
 l1 = cos (a) * cos (c) - cos (b) * sin (a) * sin (c)      
 m1 = sin (a) * cos (c) + cos (b) * cos (a) * sin (c)       
 n1 = sin (b) * sin (c)       
 l2 = -cos (a) * sin (c) + cos (b) * sin (a) * cos (c)        
 m2 = -sin (a) * sin (c) + cos (b) * cos (a) * cos (c)      
 n2 = sin (b) * cos (c)
 l3 = sin (b) * sin (a)
 m3 = -sin (b) * कॉस (a)       
 n3 = कॉस (b)

हम तीन आयामी निर्देशांक से दो आयामी में अंतिम परिवर्तन लिखते हैं:
X = l ₁ x + l ₂ y + l ₃ z
Y = m ₁ x + m ₂ y + m ₃ z
एक्स, वाई, जेड ग्राफ के लिए "आंतरिक" निर्देशांक हैं, एक्स, वाई कुल स्क्रीन निर्देशांक हैं। इस कार्य के लिए गुणांक n1, n2 और n3 की आवश्यकता नहीं है।

double[,] a; //  N x N … double X, Y; //      x for (int x = 0; x < N; x++) { for (int y = 0; y < N; y++) { X = l1() * (x - N / 2.0) + l2() * (y - N / 2.0) + l3() * a[x, y]; Y = m1() * (x - N / 2.0) + m2() * (y - N / 2.0) + m3() * a[x, y]; chart1.Series[n].Points.AddXY(X, Y); } n++; } //      y for (int y = 0; y < N; y++) { for (int x = 0; x < N; x++) { X = l1() * (x - N / 2.0) + l2() * (y - N / 2.0) + l3() * a[x, y]; Y = m1() * (x - N / 2.0) + m2() * (y - N / 2.0) + m3() * a[x, y]; chart1.Series[n].Points.AddXY(X, Y); } n++; } 

उन घटनाओं को जोड़ें जिन पर कोण बदल जाएगा और ग्राफ घूम जाएगा। उदाहरण के लिए, यह बाईं माउस बटन और कोण बी और सी के परिवर्तन को पकड़ते हुए कर्सर की गति होगी:

 bool onmove = false; Point startpos; … private void chart1_MouseDown(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left) { onmove = true; startpos = e.Location; } } private void chart1_MouseMove(object sender, MouseEventArgs e) { if (onmove) { if ((startpos.Y - eY) < 0) b--; if ((startpos.Y - eY) > 0) b++; if ((startpos.X - eX) < 0) c--; if ((startpos.X - eX) > 0) c++; if (b > 359) b = 0; if (c > 359) c = 0; if (b < 0) b = 359; if (c < 0) c = 359; drawscene(); } } private void chart1_MouseUp(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left) onmove = false; } 

परीक्षण फ़ंक्शन z = x ² + y ² पर जांचें:

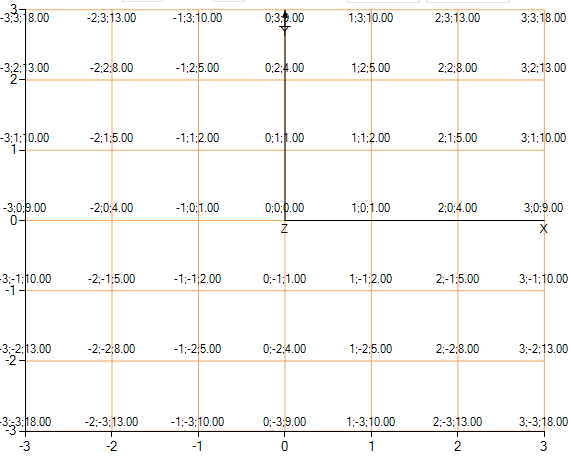फ़ंक्शन का एक शीर्ष दृश्य जहां ग्रिड दिखाई देता है और नोड्स में मान दिखाए जाते हैं।

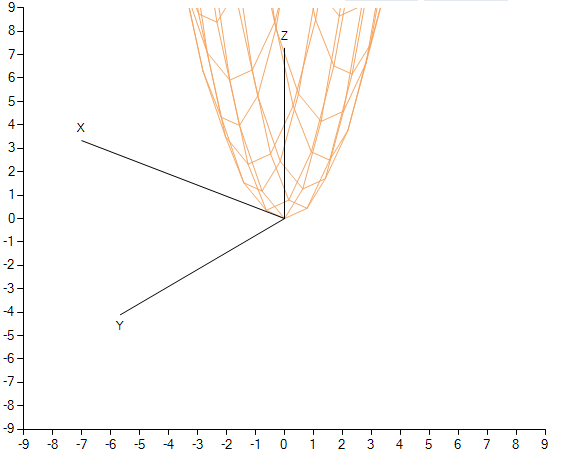फ़ंक्शन का कोण दृश्य।
यह एक अलग तरीके से कोणों को बदलने के लायक हो सकता है, जबकि सभी 3 कोणों का उपयोग करके घूमना और 1 से कम की पिच के साथ ग्रिड का उपयोग करना, लेकिन हमने स्थिति को सरल किया।

बिल्डिंग कंट्रोल्स

हम "मार्चिंग स्क्वायर" एल्गोरिथ्म का उपयोग करते हैं, विकिपीडिया पर काफी विस्तृत विवरण दिया गया है। Google इस एल्गोरिथम का वर्णन करने और इसे C # में लागू करने के लिए एक बहुत अच्छा लेख भी प्रदान करता है।
नीचे पंक्ति है:
1. शुरुआती स्थिति खोजने के लिए आवश्यक है - समोच्च कहां से आएगा।
2. फिर पड़ोसी ग्रिड नोड्स के मानों की तुलना करें जो वर्टिकल के साथ एक वर्ग बनाते हैं: (x _i , y _j ), (x _i-1 , y _j ), (x _i , y _j-1 ), (x _i-1 ) वाई _{जे -1} )।

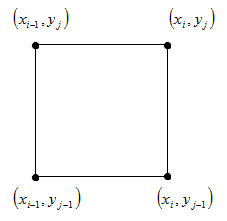
3. चरण 2 में प्राप्त मूल्य के आधार पर, बाईपास की आगे की दिशा का चयन करें, और अगले बिंदु पर जाएं, जिस पर चरण 2 को दोहराएं।
4. तब तक प्रदर्शन करें जब तक आप शुरुआती स्थिति में वापस नहीं आ जाते या ग्रिड के किनारे पर नहीं पहुँच जाते।
कुल 16 विकल्प हो सकते हैं:

हम सभी कोड फिर से नहीं लिखेंगे, हम उस लेख से कोड का हिस्सा लेंगे और इसे अपने कार्य के लिए बदल देंगे:

 enum dir { None, Up, Left, Down, Right } dir prevStep; dir nextStep; bool border; int startx, starty; void findstartpos() { for (int y = 0; y < N; y++) for (int x = 0; x < N; x++) if (arr[x, y] < Z) { startx = x; starty = y; return; } } bool check(int x, int y) { if (x == N - 1 || y == N - 1 || x == 0 || y == 0) border = true; if (x < 0 || y < 0 || x >= N || y >= N) return false; if (arr[x, y] < Z) return true; return false; } void step(int x, int y) { bool ul = check(x - 1, y - 1); bool ur = check(x, y - 1); bool dl = check(x - 1, y); bool dr = check(x, y); prevStep = nextStep; int state = 0; if (ul) state |= 1; if (ur) state |= 2; if (dl) state |= 4; if (dr) state |= 8; switch (state) { case 1: nextStep = dir.Down; break; case 2: nextStep = dir.Right; break; case 3: nextStep = dir.Right; break; case 4: nextStep = dir.Left; break; case 5: nextStep = dir.Down; break; case 6: if (prevStep == dir.Down) { nextStep = dir.Left; } else { nextStep = dir.Right; } break; case 7: nextStep = dir.Right; break; case 8: nextStep = dir.Up; break; case 9: if (prevStep == dir.Right) { nextStep = dir.Down; } else { nextStep = dir.Up; } break; case 10: nextStep = dir.Up; break; case 11: nextStep = dir.Up; break; case 12: nextStep = dir.Left; break; case 13: nextStep = dir.Down; break; case 14: nextStep = dir.Left; break; default: nextStep = dir.None; break; } } 

चलिए फिर से कोशिश करते हैं हमारे टेस्ट फंक्शन z = x ² + y ^{2 पर} :

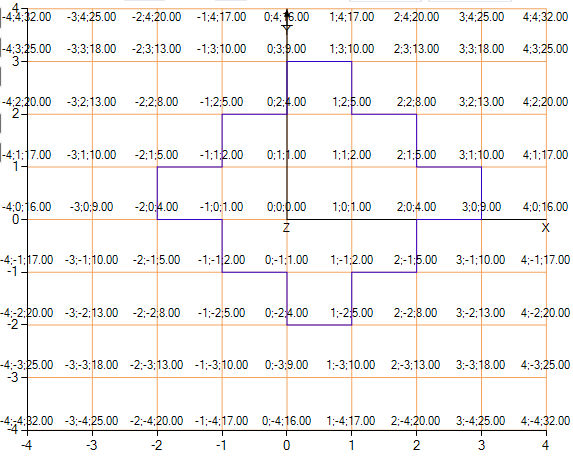
जैसा कि आप तस्वीर में देख सकते हैं, एल्गोरिथ्म ने काफी सफलतापूर्वक मुकाबला किया और उन बिंदुओं को अलग किया जहां फ़ंक्शन मान 5 से ऊपर है, लेकिन थोड़ा सही और उच्च पर। समोच्च कोणीय हो गया है, इसलिए हम प्रक्षेप करेंगे। प्रक्षेप का अर्थ यह है कि ग्रिड के पड़ोसी नोड्स में z के मूल्यों के आधार पर, हम वास्तविक समोच्च के लिए x, या y के करीब मूल्य की गणना करते हैं, जो समोच्च को अधिक प्रशंसनीय बनाता है।
हम रैखिक प्रक्षेप सूत्र का उपयोग करेंगे:
x = (Zf (x _i-1 , y _j ) / (f (x _i , y _j ) -f (x _i-1 , y _j )) + x _i-1 ,
y = (Zf (x _i , y _j-1 ) / (f (x _i , y _j ) -f (x _i , y _j-1 )) + y _j-1
जहां Z मूल्य है जिस पर अलग करना है।
एक्स समन्वय के साथ या वाई समन्वय के साथ प्रक्षेप, पिछले और अगले चरणों के लिए गति की दिशा के आधार पर चुना जाता है।
आइए इसके लिए ऐसा कोई बहुत अच्छा कोड न लिखें:

 ... List<PointF> res; ... //  x  y int dx = 0, dy = 0; switch (prevStep) { case dir.Down: dy = 1; break; case dir.Left: dx = 1;break; case dir.Up: dy = -1; break; case dir.Right: dx = -1; break; default: break; } ... double X = x0 + x; double Y = y0 + y; if (ip) //ip - interpolation { //    if (dx != 0 && prevStep == nextStep) Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1; if (dy != 0 && prevStep == nextStep) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; //    if (nextStep == dir.Down && prevStep == dir.Left) Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1; if (nextStep == dir.Left && prevStep == dir.Down) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; if (nextStep == dir.Up && prevStep == dir.Right) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; if (nextStep == dir.Up && prevStep == dir.Left) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; if (nextStep == dir.Right && prevStep == dir.Up) Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1; if (nextStep == dir.Right && prevStep == dir.Down) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; // ""  if (!(nextStep == dir.Down && prevStep == dir.Right) && !(nextStep == dir.Left && prevStep == dir.Up)) res.Add(new PointF((float)X, (float)Y)); } ... 

और हमें यह परिणाम मिलता है कि हम इसके साथ अधिक सहज हैं:


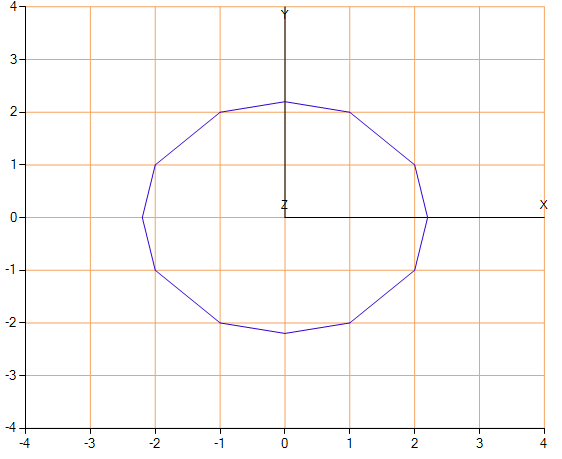
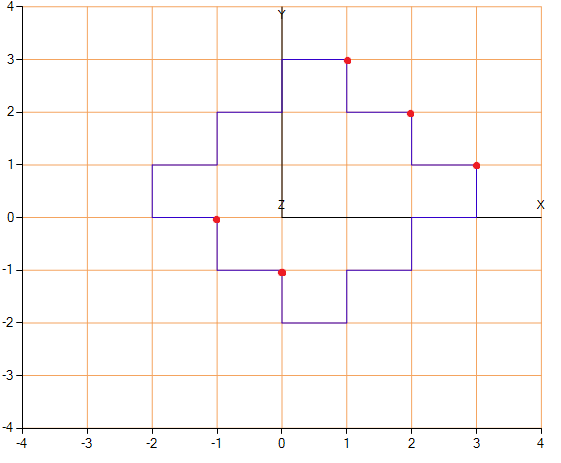"अनावश्यक बिंदुओं" का एक उदाहरण जिसे हमने बाहर रखा है।
संभावित सुधारों में से, यह ध्यान दिया जाना चाहिए कि हमारा कार्यान्वयन केवल अखंड रूप से वृद्धि (कम करने वाले लोगों के लिए, साइन को ">") कार्यों के लिए सभी आकृति का निर्माण करेगा। समय-समय पर बढ़ते और घटते कार्यों के लिए, परिवर्तन करना आवश्यक है, उदाहरण के लिए, प्रारंभिक स्थिति की खोज करने का कार्य और इसे कई बार निष्पादित करना।

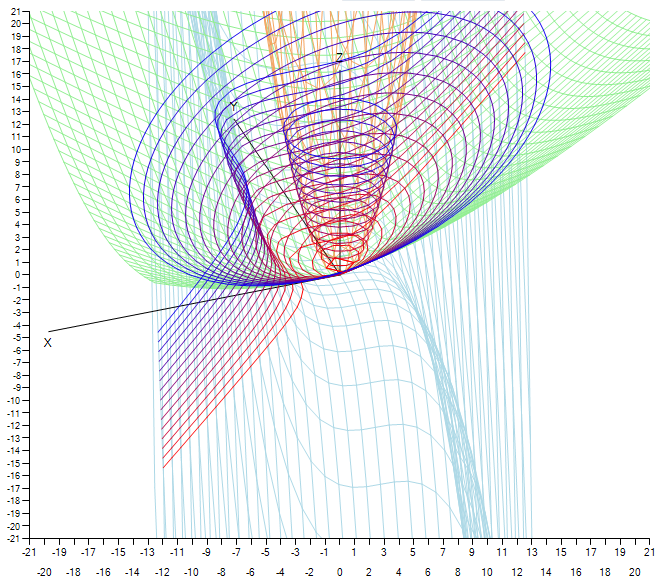अंतिम कार्यक्रम के काम का एक उदाहरण।
व्यवहार में, इसका उपयोग मानचित्रों का विश्लेषण करने, या किसी छवि में रूपरेखा की खोज करने के लिए किया जा सकता है।

कार्यक्रम का स्रोत कोड यहाँ या यहाँ डाउनलोड किया जा सकता है ।
एक बार फिर, उपयोग किए गए लिंक:
en.wikipedia.org/wiki/Rotation मैट्रिक्स
en.wikipedia.org/wiki/Euler's Angles
ru.wikipedia.org/wiki/
ru.wikipedia.org/wiki/Marching_squares
devblog.phillipspiess.com/2010/02/23/better-know-an-algorithm-1-marching-squares