दोषरहित सूचना संपीड़न। एक भाग

शुभ दिन।
आज मैं दोषरहित डेटा संपीड़न के विषय पर स्पर्श करना चाहता हूं। इस तथ्य के बावजूद कि हब पर पहले से ही कुछ एल्गोरिदम के लिए समर्पित लेख थे, मैं इस बारे में थोड़ा और विस्तार से बात करना चाहता था।
मैं गणितीय वर्णन और विवरण दोनों को सामान्य तरीके से देने की कोशिश करूंगा, ताकि हर कोई अपने लिए कुछ दिलचस्प पा सके।

इस लेख में मैं संपीड़न के मूल क्षणों और मुख्य प्रकार के एल्गोरिदम पर स्पर्श करूंगा।

संपीड़न। क्या आजकल इसकी जरूरत है?

हां, बिल्कुल। बेशक, हम सभी समझते हैं कि अब हम बड़ी मात्रा में स्टोरेज मीडिया और हाई-स्पीड डेटा ट्रांसमिशन चैनल दोनों का उपयोग कर सकते हैं। हालांकि, एक ही समय में, संचरित जानकारी के वॉल्यूम भी बढ़ रहे हैं। अगर कुछ साल पहले हमने 700-मेगाबाइट फिल्में देखीं जो एक डिस्क पर फिट होती हैं, तो आज एचडी-गुणवत्ता की फिल्में दसियों गीगाबाइट्स पर कब्जा कर सकती हैं।
बेशक, सब कुछ और सब कुछ को संपीड़ित करने के लाभ इतने अधिक नहीं हैं। लेकिन फिर भी ऐसी परिस्थितियां हैं जिनमें संपीड़न अत्यंत उपयोगी है, यदि आवश्यक नहीं है।

• ईमेल दस्तावेजों (विशेष रूप से मोबाइल उपकरणों का उपयोग करने वाले दस्तावेजों की बड़ी मात्रा)
• वेबसाइटों पर दस्तावेज़ प्रकाशित करते समय, ट्रैफ़िक को बचाने की आवश्यकता है
• स्टोरेज को बदलते या जोड़ते समय डिस्क स्थान सहेजें। उदाहरण के लिए, यह उन मामलों में होता है जहां पूंजी व्यय के लिए बजट प्राप्त करना आसान नहीं होता है, और पर्याप्त डिस्क स्थान नहीं होता है।

बेशक, आप कई अलग-अलग स्थितियों के साथ आ सकते हैं जिनमें संपीड़न उपयोगी होगा, लेकिन ये कुछ उदाहरण हमारे लिए पर्याप्त हैं।

सभी संपीड़न विधियों को दो बड़े समूहों में विभाजित किया जा सकता है: हानिपूर्ण संपीड़न और दोषरहित संपीड़न। दोषरहित संपीड़न का उपयोग उन मामलों में किया जाता है जहां जानकारी को बिट्स के लिए सटीक रूप से बहाल करने की आवश्यकता होती है। संपीड़ित करते समय यह दृष्टिकोण केवल एक ही संभव है, उदाहरण के लिए, पाठ डेटा।
कुछ मामलों में, हालांकि, सटीक जानकारी पुनर्प्राप्ति की आवश्यकता नहीं होती है और इसे एल्गोरिदम का उपयोग करने की अनुमति होती है जो हानिरहित संपीड़न को लागू करते हैं, जो दोषरहित संपीड़न के विपरीत, आमतौर पर लागू करना आसान होता है और उच्च स्तर की संग्रह प्रदान करता है।

हानिपूर्ण संपीड़न

"अच्छा पर्याप्त" डेटा गुणवत्ता बनाए रखते हुए सबसे अच्छा संपीड़न अनुपात। वे मुख्य रूप से एनालॉग डेटा - ध्वनि, चित्र को संपीड़ित करने के लिए उपयोग किए जाते हैं। ऐसे मामलों में, अनजिप की गई फ़ाइल मूल से बिट-टू-बिट तुलना स्तर पर बहुत भिन्न हो सकती है, लेकिन व्यावहारिक रूप से अधिकांश व्यावहारिक अनुप्रयोगों में मानव कान या आंख के लिए अप्रभेद्य है।

दोषरहित संपीड़न

डेटा को बिट्स के लिए सटीक रूप से पुनर्स्थापित किया जाता है, जिससे जानकारी का कोई नुकसान नहीं होता है। हालांकि, दोषरहित संपीड़न आमतौर पर सबसे खराब संपीड़न दरों को दर्शाता है।

तो, चलो दोषरहित संपीड़न एल्गोरिदम पर चलते हैं।

सार्वभौमिक दोषरहित संपीड़न विधियाँ

सामान्य मामले में, तीन बुनियादी विकल्प हैं जिन पर संपीड़न एल्गोरिदम का निर्माण किया जाता है।
विधियों का पहला समूह स्ट्रीम रूपांतरण है। यह पहले से ही संसाधित के माध्यम से नए आने वाले असम्पीडित डेटा का विवरण देता है। इस मामले में, कोई संभाव्यता की गणना नहीं की जाती है, चरित्र एन्कोडिंग केवल उस डेटा के आधार पर किया जाता है जो पहले से ही संसाधित किया गया है, जैसे कि एलजेड विधियों (अब्राहम लेम्पेल और जैकब जिवा के नाम पर)। इस मामले में, एनकोडर को पहले से ज्ञात एक निश्चित सबस्ट्रिंग की दूसरी और आगे होने वाली घटनाओं को इसकी पहली घटना के संदर्भ से बदल दिया जाता है।

विधियों का दूसरा समूह सांख्यिकीय संपीड़न विधियाँ हैं। बदले में, इन विधियों को अनुकूली (या प्रवाह), और ब्लॉक में विभाजित किया गया है।
पहले (अनुकूली) संस्करण में, नए डेटा के लिए संभावनाओं की गणना एन्कोडिंग के दौरान पहले से संसाधित किए गए डेटा पर आधारित है। इन विधियों में हफ़मैन और शैनन-फ़ानो एल्गोरिदम के अनुकूली संस्करण शामिल हैं।
दूसरे (ब्लॉक) मामले में, प्रत्येक डेटा ब्लॉक के आंकड़ों की अलग-अलग गणना की जाती है, और सबसे संकुचित ब्लॉक में जोड़ा जाता है। इनमें हफ़मैन, शैनन-फ़ानो, और अंकगणित कोडिंग विधियों के स्थिर संस्करण शामिल हैं।

विधियों का तीसरा समूह तथाकथित ब्लॉक रूपांतरण विधियां हैं। आने वाले डेटा को ब्लॉक में विभाजित किया जाता है, जो तब संपूर्ण रूप में बदल जाते हैं। उसी समय, कुछ विधियां, विशेष रूप से ब्लॉकों के क्रमचय के आधार पर, डेटा की मात्रा में महत्वपूर्ण (या कोई भी) कमी नहीं हो सकती है। हालांकि, इस तरह के प्रसंस्करण के बाद, डेटा संरचना में काफी सुधार होता है, और बाद में अन्य एल्गोरिदम द्वारा संपीड़न अधिक सफल और तेज होता है।

सामान्य सिद्धांत जिस पर डेटा संपीड़न आधारित है

सभी डेटा संपीड़न विधियाँ एक सरल तार्किक सिद्धांत पर आधारित हैं। यदि हम कल्पना करते हैं कि सबसे अधिक बार होने वाले तत्व कम कोड के साथ एन्कोड किए जाते हैं, और कम बार होने वाले लोग अधिक लंबे होते हैं, तो यह सभी डेटा को स्टोर करने के लिए कम जगह लेगा, अगर सभी तत्वों को समान लंबाई के कोड द्वारा दर्शाया गया था।
तत्वों की उपस्थिति की आवृत्ति और कोड की इष्टतम लंबाई के बीच सटीक संबंध तथाकथित शैनन के स्रोत कोडिंग प्रमेय में वर्णित है, जो अधिकतम दोषरहित संपीड़न सीमा और शैनन एन्ट्रापी निर्धारित करता है।

गणित का एक सा

यदि किसी तत्व के _i की उत्पत्ति की संभावना p (s _i ) के बराबर है, तो यह इस तत्व का प्रतिनिधित्व करने के लिए सबसे अधिक फायदेमंद होगा - ₂ p (s _i ) बिट्स लॉग करें। यदि एन्कोडिंग के दौरान यह सुनिश्चित करना संभव है कि सभी तत्वों की लंबाई ₂ पी (एस _आई ) बिट्स लॉग करने के लिए कम हो जाती है, तो पूरे एन्कोडेड अनुक्रम की लंबाई सभी संभव एन्कोडिंग विधियों के लिए न्यूनतम होगी। इसके अलावा, यदि सभी तत्वों की संभाव्यता वितरण F = {p (s _i )} स्थिर है, और तत्वों की संभाव्यता परस्पर स्वतंत्र हैं, तो कोड की औसत लंबाई की गणना की जा सकती है


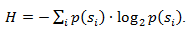
इस मान को प्रायिकता वितरण F की एन्ट्रापी या किसी निश्चित समय पर स्रोत की एन्ट्रॉपी कहा जाता है।
हालांकि, आमतौर पर एक तत्व की उपस्थिति की संभावना स्वतंत्र नहीं हो सकती है, इसके विपरीत, यह कुछ कारकों पर निर्भर करता है। इस स्थिति में, प्रत्येक नए एन्कोडेड एलिमेंट के लिए, _मैं प्रायिकता डिस्ट्रीब्यूशन F कुछ वैल्यू F _k लेगा, यानी प्रत्येक एलिमेंट F = F _k और H = H _k

दूसरे शब्दों में, हम यह कह सकते हैं कि स्रोत राज्य k में है, जो सभी तत्वों के लिए निश्चित संभावनाओं p _k (s _i ) से मेल खाता है।

इसलिए, इस सुधार को देखते हुए, औसत कोड की लंबाई के रूप में व्यक्त किया जा सकता है

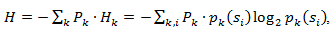
जहां पी के राज्य में स्रोत को खोजने की संभावना है।

इसलिए, इस स्तर पर, हम जानते हैं कि संपीड़न छोटे कोड के साथ अक्सर होने वाले तत्वों की जगह पर आधारित है, और इसके विपरीत, और हम यह भी जानते हैं कि कोड की औसत लंबाई कैसे निर्धारित करें। लेकिन कोड, कोडिंग क्या है और यह कैसे होता है?

मेमोरीलेस एनकोडिंग

मेमोरी के बिना कोड सबसे सरल कोड हैं जिनके आधार पर डेटा को संपीड़ित किया जा सकता है। मेमोरीलेस कोड में, एन्कोडेड डेटा वेक्टर में प्रत्येक वर्ण को बाइनरी अनुक्रमों या शब्दों के उपसर्ग सेट से एक कोडवर्ड द्वारा प्रतिस्थापित किया जाता है।
मेरी राय में, सबसे स्पष्ट परिभाषा नहीं। इस विषय पर अधिक विस्तार से विचार करें।

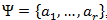
कुछ अक्षर बताए जाएं कुछ (परिमित) अक्षरों से मिलकर। हम वर्णों के प्रत्येक परिमित अनुक्रम को इस वर्णमाला (A = a, a, ₂ , ..., _n ) शब्द से कहते हैं , और इस शब्द की लंबाई n है।

एक अन्य वर्णमाला भी बताइए । इसी तरह, इस वर्णमाला के शब्द को B के रूप में निरूपित करें।

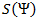
हम वर्णमाला के सभी गैर-रिक्त शब्दों के सेट के लिए दो और संकेतन प्रस्तुत करते हैं। चलो - पहले वर्णमाला में गैर-खाली शब्दों की संख्या, और - दूसरे में।

आइए एक मैपिंग F भी दें जो प्रत्येक शब्द A के साथ पहले वर्णमाला के दूसरे शब्द B = F (A) से जुड़ा हो। तब B शब्द को A शब्द का कोड कहा जाएगा, और मूल शब्द से उसके कोड में परिवर्तन को कोडिंग कहा जाएगा।

चूंकि शब्द में एक अक्षर भी हो सकता है, इसलिए हम पहले वर्णमाला के अक्षरों के पत्राचार और दूसरे से संबंधित शब्दों की पहचान कर सकते हैं:
ए _१ <-> बी _१
एक ₂ <-> बी ₂
...
a _n <-> B _n

इस पत्राचार को एक सर्किट कहा जाता है, और oted द्वारा निरूपित किया जाता है।
इस स्थिति में, बी ₁ , बी ₂ , ..., बी _एन को प्राथमिक कोड कहा जाता है, और उनकी मदद से एन्कोडिंग के प्रकार को वर्णमाला एन्कोडिंग कहा जाता है । बेशक, हम में से अधिकांश इस प्रकार के कोडिंग के साथ आए हैं, भले ही हम उन सभी को नहीं जानते हैं जो मैंने ऊपर वर्णित किया था।

इसलिए, हमने वर्णमाला, शब्द, कोड और कोडिंग की अवधारणाओं पर निर्णय लिया। अब हम एक उपसर्ग की अवधारणा का परिचय देते हैं।

बता दें कि बी शब्द का फॉर्म B = B'B '' है। तब B 'को B शब्द की शुरुआत या उपसर्ग कहा जाता है, और B' 'इसका अंत है। यह एक काफी सरल परिभाषा है, लेकिन यह ध्यान दिया जाना चाहिए कि किसी भी शब्द बी के लिए, एक निश्चित शब्द “(" स्थान ") और बी शब्द ही दोनों शुरुआत और अंत माना जा सकता है।

इसलिए, हम मेमोरी के बिना कोड की परिभाषा को समझने के करीब आते हैं। अंतिम परिभाषा जिसे हमें समझने की आवश्यकता है वह उपसर्ग सेट है। एक योजना any में एक उपसर्ग की संपत्ति होती है यदि किसी भी 1≤i, jr, i, j के लिए, B शब्द _I B शब्द का उपसर्ग नहीं है।
सीधे शब्दों में कहें, एक उपसर्ग सेट एक परिमित सेट है जिसमें कोई तत्व किसी अन्य तत्व का उपसर्ग (या शुरुआत) नहीं है। इस तरह के एक सेट का एक सरल उदाहरण है, उदाहरण के लिए, नियमित वर्णमाला।

इसलिए, हमने आधारभूत परिभाषाएं निकालीं। तो स्मृतिहीन कोडिंग कैसे होती है?
यह तीन चरणों में होता है।

1. मूल संदेश के वर्णों का एक वर्णमाला Ψ संकलित किया जाता है, जिसके साथ वर्णमाला के पात्रों को संदेश में उनके होने की संभावना के अवरोही क्रम में क्रमबद्ध किया जाता है।
2. वर्णमाला से प्रत्येक प्रतीक Ψ उपसर्ग सेट from से एक निश्चित शब्द B _i से जुड़ा हुआ है।
3. प्रत्येक वर्ण एन्कोडेड है, इसके बाद एक डेटा स्ट्रीम में कोड के संयोजन, जो संपीड़न का परिणाम होगा।

इस विधि का वर्णन करने वाले विहित एल्गोरिदम में से एक हफ़मैन एल्गोरिथम है।

हफ़मैन एल्गोरिदम

हफमैन एल्गोरिथ्म इनपुट डेटा ब्लॉक में समान बाइट्स की घटना की आवृत्ति का उपयोग करता है, और कम लंबाई के बिट्स की एक श्रृंखला के अक्सर होने वाले ब्लॉक को जोड़ता है, और इसके विपरीत। यह कोड न्यूनतम बेमानी है। मामले पर विचार करें, जब इनपुट स्ट्रीम की परवाह किए बिना, आउटपुट स्ट्रीम की वर्णमाला में केवल 2 वर्ण होते हैं - शून्य और एक।

सबसे पहले, हफ़मैन एल्गोरिथ्म के साथ कोडिंग करते समय, हमें सर्किट cod के निर्माण की आवश्यकता होती है। यह निम्नानुसार किया जाता है:

1. इनपुट वर्णमाला के सभी अक्षरों को संभाव्यता के अवरोही क्रम में क्रमबद्ध किया जाता है। आउटपुट स्ट्रीम की वर्णमाला के सभी शब्द (जो हम एनकोड करेंगे) को शुरू में खाली माना जाता है (मुझे याद है कि आउटपुट स्ट्रीम की वर्णमाला में केवल प्रतीकों {0,1} शामिल हैं)।
2. दो प्रतीकों एक _j-1 और इनपुट स्ट्रीम के एक _जे , जिसमें घटना की कम से कम संभावना है, को एक "छद्म-प्रतीक" में जोड़ा जाता है जिसमें संभाव्यता p के साथ इसमें शामिल प्रतीकों की संभावनाओं के योग के बराबर होता है। फिर हम B शब्द की शुरुआत में B _j-1 , और 1 शब्द B की शुरुआत करते हैं, जो बाद में क्रमशः _j-1 और _j अक्षर का कोड होगा।
3. हम इन वर्णों को मूल संदेश की वर्णमाला से हटाते हैं, लेकिन इस वर्णमाला में उत्पन्न छद्म-चिह्न को जोड़ते हैं (स्वाभाविक रूप से, इसे सही जगह पर वर्णमाला में डाला जाना चाहिए, इसकी संभावना को ध्यान में रखते हुए)।

चरण 2 और 3 तब तक दोहराए जाते हैं जब तक कि वर्णमाला में केवल 1 छद्म चरित्र न बचा हो, जिसमें वर्णमाला के सभी मूल वर्ण शामिल हों। इसके अलावा, प्रत्येक चरण पर और प्रत्येक वर्ण के लिए, संबंधित शब्द B _i (एक या शून्य जोड़कर) बदलता है, इस प्रक्रिया के पूरा होने के बाद, वर्णमाला का प्रत्येक प्रारंभिक वर्ण _{i i} एक निश्चित कोड B के अनुरूप होगा।

बेहतर चित्रण के लिए, एक छोटे से उदाहरण पर विचार करें।
मान लें कि हमारे पास केवल चार वर्णों से मिलकर एक वर्णमाला है - {a ₁ , a ₂ , a, ₃ }। यह भी मान लें कि इन प्रतीकों की घटना की संभावनाएं समान हैं, क्रमशः, पी ₁ = 0.5; पी ₂ = 0.24; पी ₃ = 0.15; पी ₄ = 0.11 (सभी संभावनाओं का योग स्पष्ट रूप से एक के बराबर है)।

तो, हम इस वर्णमाला के लिए सर्किट का निर्माण करेंगे।

1. कम से कम संभाव्यता (0.11 और 0.15) के साथ दो वर्णों को p 'के छद्म वर्ण में संयोजित करें।
2. हम संयुक्त वर्णों को हटाते हैं, और परिणामस्वरूप छद्म वर्ण को वर्णमाला में सम्मिलित करते हैं।
3. दो वर्णों को कम से कम प्रायिकता (0.24 और 0.26) के साथ p '' छद्म वर्ण में मिलाएँ।
4. हम संयुक्त वर्णों को हटाते हैं, और परिणामस्वरूप छद्म वर्ण को वर्णमाला में सम्मिलित करते हैं।
5. अंत में, शेष दो पात्रों को मिलाएं और पेड़ की चोटी प्राप्त करें।

यदि आप इस प्रक्रिया का वर्णन करते हैं, तो आपको निम्नलिखित जैसा कुछ मिलता है:


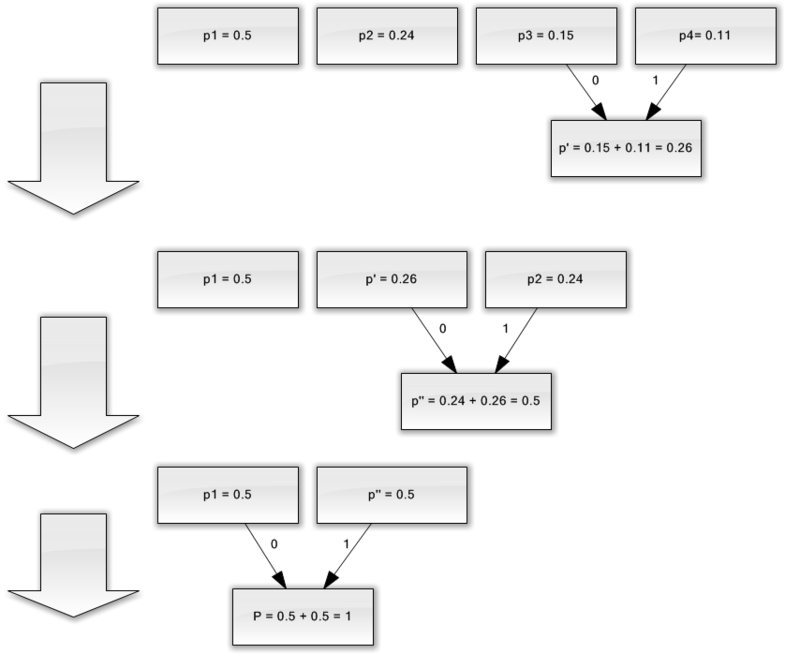
जैसा कि आप देख सकते हैं, प्रत्येक मर्ज के साथ, हम वर्णों को मर्ज किए जाने के लिए कोड 0 और 1 असाइन करते हैं।
इस प्रकार, जब पेड़ बनाया जाता है, तो हम आसानी से प्रत्येक वर्ण के लिए कोड प्राप्त कर सकते हैं। हमारे मामले में, कोड इस तरह दिखाई देंगे:

एक _१ = ०
एक ₂ = 11
एक ₃ = 100
एक ₄ = 101

चूंकि इनमें से कोई भी कोड किसी अन्य का उपसर्ग नहीं है (अर्थात, हमें कुख्यात उपसर्ग सेट मिला है), हम उत्पादन कोड में प्रत्येक कोड को विशिष्ट रूप से पहचान सकते हैं।
इसलिए, हमने पाया है कि सबसे अक्सर चरित्र सबसे छोटे कोड द्वारा एन्कोड किया गया है, और इसके विपरीत।
यदि हम मानते हैं कि शुरू में प्रत्येक चरित्र को संग्रहीत करने के लिए एक बाइट का उपयोग किया गया था, तो हम गणना कर सकते हैं कि हम डेटा को कम करने में कितना सक्षम थे।

मान लीजिए कि हमारे पास इनपुट में 1000 वर्णों की एक स्ट्रिंग है, जिसमें चरित्र _{1 1} बार 500 बार, एक ₂ 240, ₃ 150, और ₄ 110 बार हुआ।

प्रारंभ में, इस स्ट्रिंग ने 8000 बिट्स पर कब्जा कर लिया। कोडिंग के बाद, हम stringp _i l _i = 500 * 1 + 240 * 2 + 150 * 3 + 110 * 3 = 1760 बिट्स की लंबाई के साथ एक स्ट्रिंग प्राप्त करते हैं। इसलिए, हम 4.54 बार डेटा को सेक करने में सक्षम थे, स्ट्रीम के प्रत्येक प्रतीक को एन्कोडिंग के लिए औसतन 1.76 बिट्स खर्च करते हैं।

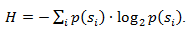
आपको याद दिला दूं कि शैनन के अनुसार, कोड की औसत लंबाई है । इस समीकरण में हमारे संभाव्यता मानों को प्रतिस्थापित करते हुए, हमें कोड की औसत लंबाई 1.75496602732291 के बराबर मिलती है, जो हमारे द्वारा प्राप्त किए गए परिणाम के बहुत करीब है।
हालांकि, यह ध्यान में रखा जाना चाहिए कि डेटा के अलावा, हमें एन्कोडिंग तालिका को संग्रहीत करने की आवश्यकता है, जो एन्कोडेड डेटा के अंतिम आकार को थोड़ा बढ़ा देगा। जाहिर है, अलग-अलग मामलों में एल्गोरिथ्म के विभिन्न रूपों का उपयोग किया जा सकता है - उदाहरण के लिए, कभी-कभी पूर्वनिर्धारित संभाव्यता तालिका का उपयोग करना अधिक कुशल होता है, और कभी-कभी यह संकुचित डेटा के माध्यम से गतिशील रूप से संकलित करना आवश्यक होता है।

निष्कर्ष

इसलिए, इस लेख में मैंने उन सामान्य सिद्धांतों के बारे में बात करने की कोशिश की जिनके द्वारा दोषरहित संपीड़न होता है, और मैंने एक कैनोनिकल एल्गोरिदम - हफ़मैन कोडिंग की भी जांच की।
यदि लेख हाबोर-समुदाय के स्वाद के लिए है, तो मुझे अगली कड़ी लिखने में खुशी होगी, क्योंकि दोषरहित संपीड़न के बारे में कई और दिलचस्प बातें हैं; ये दोनों शास्त्रीय एल्गोरिदम और प्रारंभिक डेटा रूपांतरण हैं (उदाहरण के लिए, बरोज़-व्हीलर ट्रांसफ़ॉर्म), और निश्चित रूप से, ध्वनि, वीडियो और छवियों को संपीड़ित करने के लिए विशिष्ट एल्गोरिदम (सबसे दिलचस्प विषय, मेरी राय में)।

साहित्य

• वैटोलिन डी।, रतुश्नायक ए।, स्मिरनोव एम। युकिन वी। डेटा संपीड़न के तरीके। डिवाइस अभिलेखागार, छवि और वीडियो संपीड़न; आईएसबीएन 5-86404-170-एक्स; 2003 वर्ष
• डी। सलोमन। डेटा, छवि और ध्वनि का संपीड़न; आईएसबीएन 5-94836-027-एक्स; 2004।
• www.wikipedia.org