शोर पेर्लिन (Perlin शोर)

शुभ दिन। मैं आपके ध्यान में Perlin शोर ( यह एक ) के बारे में एक लेख का अनुवाद लाता हूं। इस लेख के लिंक पहले से ही एक हब ( यहाँ ) पर दिए गए हैं, लेकिन मैं लेख के अनुवाद में नहीं आया। इसलिए मुझे उम्मीद है कि कोई इसे उपयोगी पा सकता है।

कई लोगों को अप्रत्याशितता पैदा करने, वस्तुओं की गति और व्यवहार को अधिक स्वाभाविक बनाने या बनावट उत्पन्न करने के लिए कार्यक्रमों में एक यादृच्छिक संख्या जनरेटर का उपयोग करना पड़ा। यादृच्छिक संख्या जनरेटर, ज़ाहिर है, अनुप्रयोग के अपने क्षेत्र हैं, लेकिन कभी-कभी उनका उत्पादन प्राकृतिक प्रतीत होने के लिए बहुत कठिन हो सकता है। इस लेख में, हम एक ऐसा कार्य प्रस्तुत करते हैं जिसमें अनुप्रयोगों की एक बहुत विस्तृत श्रृंखला है, जितना मैं सोच सकता था, उससे अधिक है, लेकिन ज्यादातर जहां भी आपको प्राकृतिक दिखने के लिए कुछ चाहिए। इसके अलावा, उत्पादन आसानी से अपनी आवश्यकताओं के लिए अनुकूलित किया जा सकता है।

यदि आप प्रकृति में कई चीजों को देखते हैं, तो आप देखेंगे कि वे भग्न हैं। उनके पास विस्तार के विभिन्न स्तर हैं। एक विशिष्ट उदाहरण एक पर्वत श्रृंखला की रूपरेखा है। इसमें ऊँचाई (पर्वत), मध्यम परिवर्तन (पहाड़ियाँ), छोटे रूपांतर (बोल्डर), छोटे परिवर्तन (पत्थर), इत्यादि में महत्वपूर्ण अंतर हैं। किसी भी चीज को देखें: मैदान पर घास के धब्बे, समुद्र में लहरें, चींटियों की आवाजाही, पेड़ की शाखाओं की आवाजाही, संगमरमर के पैटर्न, हवा। ये सभी घटनाएं बड़े और छोटे बदलावों में खुद को एक ही पैटर्न पर उधार देती हैं। पेर्लिन का शोर समारोह विभिन्न तराजू में शोर कार्यों को जोड़कर इसे फिर से बनाता है।

पेरलिन शोर फ़ंक्शन बनाने के लिए, आपको दो चीज़ें चाहिए, एक शोर फ़ंक्शन और एक इंटरपोलेशन फ़ंक्शन।

शोर समारोह

शोर समारोह अनिवार्य रूप से एक यादृच्छिक संख्या जनरेटर नमूना है। यह एक पूर्णांक को एक पैरामीटर के रूप में लेता है, और उस पैरामीटर के आधार पर एक यादृच्छिक संख्या देता है। यदि आप एक ही पैरामीटर को दो बार पास करते हैं, तो यह एक ही नंबर को दो बार लौटाएगा। यह बहुत महत्वपूर्ण है कि वह इस तरह से व्यवहार करे, अन्यथा उससे कोई मतलब नहीं होगा।

यहां एक ग्राफ है जो एक शोर फ़ंक्शन का एक उदाहरण दिखा रहा है। X अक्ष पर प्रत्येक बिंदु पर 0 से 1 तक का यादृच्छिक मान असाइन किया गया है।

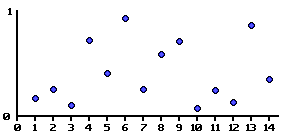
मूल्यों के बीच सहज प्रक्षेप द्वारा, हम एक निरंतर फ़ंक्शन निर्धारित कर सकते हैं जो एक गैर-पूर्णांक को एक पैरामीटर के रूप में लेता है।

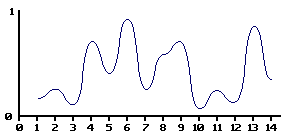
मूल्यों को प्रक्षेपित करने के विभिन्न तरीके बाद में इस लेख में होंगे।

परिभाषित

आगे बढ़ने से पहले, मुझे यह निर्धारित करने दें कि मुझे आयाम और आवृत्ति से क्या मतलब है। यदि आपने भौतिकी का अध्ययन किया है, तो आप अच्छी तरह से आयाम और आवृत्ति की अवधारणा पर आ सकते हैं जैसा कि एक साइन लहर पर लागू होता है।

साइन लहर

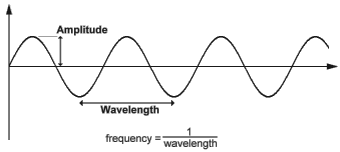
(आयाम - आयाम, तरंग दैर्ध्य - तरंग दैर्ध्य, आवृत्ति - आवृत्ति)
तरंग दैर्ध्य एक शीर्ष से दूसरे तक की दूरी है। आयाम तरंग की ऊँचाई है। आवृत्ति को 1 / (तरंग दैर्ध्य) के रूप में परिभाषित किया गया है।

शोर की लहर

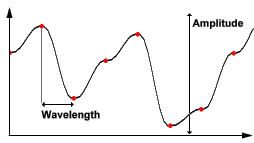
इस शोर फ़ंक्शन के ग्राफ पर, उदाहरण के लिए, लाल डॉट्स फ़ंक्शन को मापने के द्वारा निर्धारित यादृच्छिक मानों को इंगित करते हैं।
इस मामले में, आयाम न्यूनतम और अधिकतम मूल्यों के बीच का अंतर है जो फ़ंक्शन हो सकता है। तरंग दैर्ध्य एक लाल स्थान से दूसरे स्थान पर दूरी है। फिर से, आवृत्ति को 1 / (तरंग दैर्ध्य) के रूप में परिभाषित किया गया है।

एक पेर्लिन शोर समारोह बनाना

अब, यदि आप बहुत से ऐसे कार्य करते हैं, विभिन्न आवृत्तियों और आयामों के साथ, आप अच्छी तरह से शोर करने वाले फ़ंक्शन बनाने के लिए उन सभी को एक साथ जोड़ सकते हैं। यह पेरलिन शोर का एक कार्य है।
निम्न शोर सुविधाएँ लें

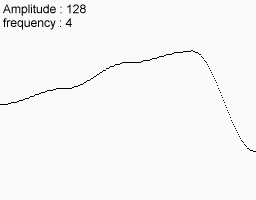
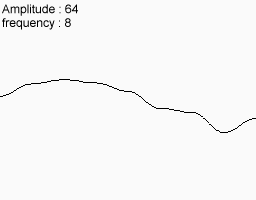
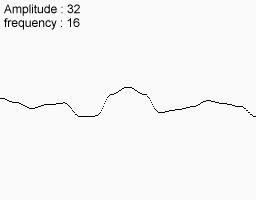
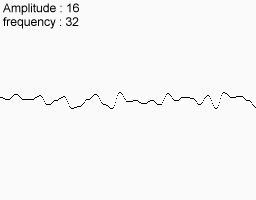
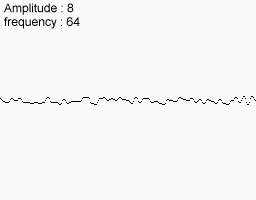
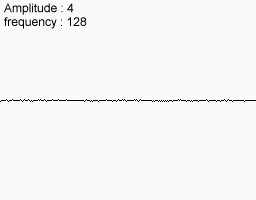
उन्हें एक साथ मिलाएं और यही आपको अंत में मिलता है।

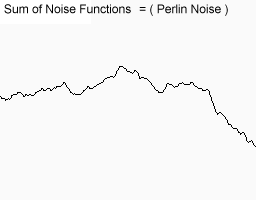
आप देखते हैं कि इस फ़ंक्शन में बड़े, मध्यम और छोटे बदलाव हैं। आप कल्पना भी कर सकते हैं कि यह पर्वत श्रृंखला जैसी दिखती है। वास्तव में, इस पद्धति का उपयोग करके कई कंप्यूटर परिदृश्य बनाए जाते हैं। बेशक वे 2 डी शोर का उपयोग करते हैं जो मुझे इस समय मिला है।
बेशक, आप दो आयामों के लिए एक ही कर सकते हैं। 2 डी में कुछ शोर सुविधाएँ

इन सभी कार्यों को एक साथ जोड़ने पर हमें एक शोर चित्र मिलता है।

प्रतिरोध (हठ)

जब आप इन शोर कार्यों को एक साथ जोड़ते हैं, तो आपको आश्चर्य हो सकता है कि उनमें से प्रत्येक किस प्रकार के आयाम और आवृत्ति का उपयोग करता है। एक आयामी उदाहरण में, दो बार आवृत्ति और आधे आयाम का उपयोग प्रत्येक बाद में जोड़े गए शोर फ़ंक्शन के लिए किया गया था। यह एक काफी सामान्य घटना है। इस प्रकार, वास्तव में, बहुत से लोग हर चीज का उपयोग करने पर भी विचार नहीं करते हैं। हालांकि, आप विभिन्न विशेषताओं और विभिन्न आवृत्तियों और एम्पलीट्यूड का उपयोग करके हर चरण में पेर्लिन फ़ंक्शन शोर बना सकते हैं। उदाहरण के लिए, चिकनी पहाड़ियों को बनाने के लिए, आप कम आवृत्तियों पर बड़े आयामों और उच्च आवृत्तियों पर बहुत छोटे आयामों के साथ पेरलिन शोर कार्यों का उपयोग कर सकते हैं। या आप कम आवृत्तियों के लिए छोटे आयामों का चयन करके एक सपाट लेकिन बहुत चट्टानी विमान बना सकते हैं।
इसे और अधिक सरल रूप से समझाने के लिए, और हर समय "आयाम" और "आवृत्ति" शब्दों को दोहराने से बचने के लिए, प्रत्येक आयाम और प्रत्येक आवृत्ति को निर्धारित करने के लिए एक एकल संख्या का उपयोग किया जाता है। इस मूल्य को दृढ़ता कहा जाता है। इसके सटीक अर्थ के बारे में कुछ अनिश्चितता है। यह शब्द मूल रूप से मैंडेलब्रोट द्वारा गढ़ा गया था, जो भग्न की खोज के पीछे थे। उन्होंने कम प्रतिरोध वाले उच्च आवृत्तियों के साथ शोर की पहचान की। मेरा दोस्त मैट भी दृढ़ता की अवधारणा के साथ आया था, लेकिन इसे दूसरे तरीके से परिभाषित किया। ईमानदारी से, मैं मैट की परिभाषा पसंद करता हूं।
क्षमा करें, मैंडलब्रॉट।
इस प्रकार, दृढ़ता की हमारी परिभाषा इस प्रकार है:

frequency() = 2^i amplitude() = persistence()^i 

जहां मैं i-th जोड़ा शोर फ़ंक्शन है।
पेरलिन शोर आउटपुट पर दृढ़ता के प्रभाव को स्पष्ट करने के लिए, नीचे दिए गए आरेखों पर एक नज़र डालें।
वे जोड़े जाने वाले फ़ंक्शन के शोर घटक को दर्शाते हैं, मूल्य को संग्रहीत करने का प्रभाव, और, परिणामस्वरूप, पेरलिन शोर फ़ंक्शन।

स्थायित्व = 1/4

आवृत्तियों: 1, 2, 4, 8, 16, 32
=
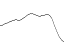
आयाम: 1, 1/4, 1/16, 1/64, 1/256, 1/1024

स्थायित्व = १/२

आवृत्तियों: 1, 2, 4, 8, 16, 32
=
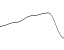
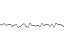
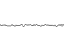
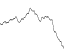
आयाम: 1, 1/2, 1/4, 1/8, 1/16, 1/32

स्थायित्व = 1 / रूट 2

आवृत्तियों: 1, 2, 4, 8, 16, 32
=
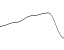
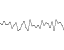
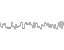
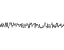
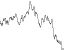
आयाम: 1, 1 / 1.414, 1/2, 1 / 2.828, 1/4, 1 / 5.656

स्थायित्व = १

आवृत्तियों: 1, 2, 4, 8, 16, 32
=
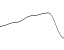
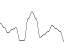
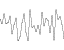
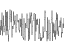
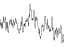
एम्प्लिट्यूड: 1, 1, 1, 1, 1, 1

सप्टक

प्रत्येक जोड़ा बाद के शोर समारोह को एक सप्तक कहा जाता है। इसका कारण यह है कि प्रत्येक शोर फ़ंक्शन में पिछले एक की तुलना में दो बार आवृत्ति होती है। संगीत में, सप्तक के पास भी यह गुण होता है।
आपके द्वारा जोड़े गए कितने सप्तक पूरी तरह से आपके ऊपर हैं। आप जितने चाहें उतने या कुछ जोड़ सकते हैं। हालाँकि, मैं आपको कुछ सलाह देता हूँ। यदि आप एक स्क्रीन पर छवि को प्रस्तुत करने के लिए पेरलिन के शोर कार्यों का उपयोग करते हैं, तो एक समय आएगा जब ऑक्टेव को प्रदर्शित करने के लिए बहुत अधिक आवृत्ति हो सकती है। बहुत उच्च शोर फ़ंक्शन पर सभी बारीक विवरणों को पुन: पेश करने के लिए बस स्क्रीन पर पर्याप्त पिक्सेल नहीं हो सकते हैं। पर्लिन शोर के कुछ कार्यान्वयन स्क्रीन संकल्प (या अन्य माध्यम) की सीमा तक पहुंचने तक स्वचालित रूप से शोर कार्यों में जोड़ते हैं।
इसके अलावा, शोर को जोड़ने पर रोकना बुद्धिमान है जब परिणाम को प्रभावित करने के लिए उनका आयाम बहुत छोटा हो जाता है। जब वास्तव में ऐसा होता है तो प्रतिरोध के स्तर पर निर्भर करता है, पेरलिन फ़ंक्शन का सामान्य आयाम और स्क्रीन रिज़ॉल्यूशन का बिट (या कुछ और)।

एक शोर समारोह बनाएँ

हम शोर समारोह में क्या देख रहे हैं? अनिवार्य रूप से एक यादृच्छिक संख्या जनरेटर। हालांकि, अन्य यादृच्छिक संख्या जनरेटर के विपरीत आप उन कार्यक्रमों में मुठभेड़ करते हैं जो आपको हर बार जब आप उन्हें कॉल करते हैं तो अलग-अलग यादृच्छिक संख्याएं देते हैं, ये शोर फ़ंक्शन एक या अधिक मापदंडों से गणना किए गए यादृच्छिक संख्या का उत्पादन करते हैं। यही है, हर बार जब आप एक ही नंबर दर्ज करते हैं, तो शोर फ़ंक्शन इस नंबर के लिए पहले की तरह ही जवाब देगा। लेकिन एक और नंबर दर्ज करने पर, यह एक और नंबर लौटाएगा।
खैर, मैं यादृच्छिक संख्या जनरेटर के बारे में ज्यादा नहीं जानता, इसलिए मैंने तलाश शुरू की, और यहां मुझे एक मिला। वह बहुत अच्छा लग रहा था। यह -1.0 से 1.0 तक फ्लोटिंग पॉइंट नंबर देता है।

  function IntNoise(32-bit integer: x) x = (x<<13) ^ x; return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0); end IntNoise function 

अब, आप शायद कई अलग-अलग यादृच्छिक संख्या जनरेटर चाहते हैं, इसलिए मैं ऊपर दिए गए कोड की कुछ प्रतियां बनाने का सुझाव देता हूं, लेकिन थोड़ा अलग संख्याओं का भी उपयोग कर रहा हूं। ये बड़े, खौफनाक-दिखने वाले नंबर सभी प्राइम नंबर हैं, इसलिए आप बस एक ही आकार के कुछ अन्य प्राइम नंबर का उपयोग कर सकते हैं। इस प्रकार, आपके लिए यादृच्छिक संख्याओं को खोजना आसान बनाने के लिए, मैंने आपके लिए primes को सूचीबद्ध करने के लिए एक छोटा कार्यक्रम लिखा। आप उसे शुरुआती और अंतिम संख्या दे सकते हैं, और वह उन दोनों के बीच के सभी अपराधों को खोजेगी। स्रोत कोड भी शामिल है, इसलिए आप एक यादृच्छिक प्राइम नंबर ( प्रोग्राम और कोड ) बनाने के लिए इसे आसानी से अपने कार्यक्रमों में शामिल कर सकते हैं।
( संसाधन को कम करने के लिए नहीं, मैं पूरी तरह से यहां कोड पोस्ट करता हूं, क्योंकि इसमें बहुत कुछ नहीं है )

 #include <stdlib.h> #include <iostream.h> #include <math.h> inline long sqrt(long i) { long r,rnew=1,rold=r; do { rold=r; r=rnew; rnew = (r+(i/r)); rnew >>= 1; } while(rold != rnew); return rnew; } inline int isprime(long i) { long si,j; si = sqrt(i); for (j=2; (j<=si); j++) { if (i%j == 0) return 0; } return 1; } void main(int argc, char *argv[]) { long i,i1,i2,f=0; if (argc < 2) { cout << endl << endl; cout << "Prime number finder: Hugo Elias 1998" << endl << "http://freespace.virgin.net/hugo.elias" << endl << endl; cout << "Usage:" << endl << " primes ab > primes.txt" << endl << endl; cout << "will find all primes between a and b" << endl << "and will write the results to the file PRIMES.TXT" << endl; return; } i1 = atol(argv[1]); i2 = atol(argv[2]); for (i=i1; i<i2; i++) if (isprime(i)) { f++; if (f==16) { cout << endl; f=0; } cout << i << " "; } } 

प्रक्षेप

अपना शोर फ़ंक्शन बनाने के बाद, आपको उन मानों को सुचारू करने की आवश्यकता होती है जो इसे वापस करते हैं। फिर से, आप अपनी पसंद की कोई भी विधि चुन सकते हैं, लेकिन कुछ दूसरों की तुलना में बेहतर दिखती हैं। मानक प्रक्षेप कार्यों में तीन इनपुट होते हैं, ए, बी, उनके बीच प्रक्षेप के लिए मान, और एक्स, जो 0 से 1 तक मान लेता है। प्रक्षेप फ़ंक्शन एक्स के मूल्य के आधार पर ए और बी के बीच एक मान लौटाता है। यदि x 0 है, तो a लौटाया जाता है, और x = 1 के लिए, तो b वापस कर दिया जाता है। यदि x 0 और 1 के बीच है, तो a और b के बीच कुछ मान लौटाता है।

रैखिक प्रक्षेप

यह भयानक लग रहा है, सस्ते "प्लाज्मा" की तरह है कि कई परिदृश्य बनाने के लिए उपयोग करते हैं। यह एक सरल एल्गोरिथ्म है, हालांकि, और मुझे लगता है कि अगर आप वास्तविक समय में पेर्लिन शोर करने की कोशिश करते हैं तो यह बहाना होगा।

 function Linear_Interpolate(a, b, x) return a*(1-x) + b*x end of function 

कोसाइन प्रक्षेप

यह विधि रैखिक प्रक्षेप की तुलना में एक चिकनी वक्र देती है। यह स्पष्ट रूप से सबसे अच्छा परिणाम है और प्रयास के लायक है यदि आप गति में बहुत कम नुकसान उठा सकते हैं।

 function Cosine_Interpolate(a, b, x) ft = x * 3.1415927 f = (1 - cos(ft)) * .5 return a*(1-f) + b*f end of function 

घन प्रक्षेप

यह विधि बहुत ही सहज परिणाम देती है, लेकिन आप गति में इसके लिए भुगतान करते हैं। ईमानदारी से, मुझे यकीन नहीं है कि यह कोसाइन प्रक्षेप से बेहतर परिणाम देगा, लेकिन यहां यह आपके विवेक पर किसी भी मामले में है। यह थोड़ा पेचीदा मामला है, इसलिए सावधान रहें। यदि पहले, प्रक्षेप फ़ंक्शन के लिए तीन इनपुट थे, तो क्यूबिक इंटरपोलेशन पांच लेता है। ए और बी के बजाय, अब आपको पहले की तरह x के साथ v0, v1, v2 और v3 की आवश्यकता है।

v0 = पॉइंट टू ए
v1 = बिंदु a
v2 = बिंदु बी
v3 = बिंदु b के बाद

  function Cubic_Interpolate(v0, v1, v2, v3,x) P = (v3 - v2) - (v0 - v1) Q = (v0 - v1) - P R = v2 - v0 S = v1 return Px3 + Qx2 + Rx + S end of function 

चिकना शोर

प्रक्षेप के अलावा, आप शोर समारोह के उत्पादन को भी कम कर सकते हैं ताकि यह कम यादृच्छिक लग सके, साथ ही 2 डी और 3 डी संस्करणों में कम क्षेत्र। चौरसाई आपकी अपेक्षा से अधिक करेगा, और जिस किसी ने भी एक चौरसाई फिल्टर या फायर एल्गोरिथ्म लिखा है, उसे पहले से ही इस प्रक्रिया से परिचित होना चाहिए। निर्देशांक में शोर फ़ंक्शन के मान लेने के बजाय, आप इस मान का औसत और पड़ोसी निर्देशांक में मान ले सकते हैं। यदि यह स्पष्ट नहीं है, तो नीचे दिए गए छद्म कोड पर एक नज़र डालें।
एक छोटे आरेख में, सुचारू शोर समारोह और चौरसाई के बिना एक ही शोर समारोह के बीच अंतर को चित्रित किया गया है।
आप देख सकते हैं कि सुचारू शोर फ़ंक्शन को सुचारू किया जाता है, कभी भी अन-स्मूथ शोर फ़ंक्शन के चरम तक नहीं पहुंचता है, और आवृत्ति लगभग आधी है। 1-आयामी शोर को चौरसाई करने में कोई मतलब नहीं है, क्योंकि यह वास्तव में एकमात्र प्रभाव है। चौरसाई 2 या तीन आयामों में अधिक उपयोगी हो जाती है, जहां शोर के प्रभाव को कम करना है।
दुर्भाग्य से, यह इसके विपरीत को भी कम करता है। आप इसे चिकनी बनाते हैं, शोर स्पष्ट रूप से चापलूसी होगा।

1-आयामी चौरसाई शोर

  function Noise(x) . . end function function SmoothNoise_1D(x) return Noise(x)/2 + Noise(x-1)/4 + Noise(x+1)/4 end function 

2-आयामी चौरसाई शोर

  function Noise(x, y) . . end function function SmoothNoise_2D(x>, y) corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16 sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8 center = Noise(x, y) / 4 return corners + sides + center end function 

यह सब एक साथ रखना

अब आप सब कुछ जानते हैं, इसलिए आपके द्वारा सीखी गई हर चीज को एक साथ रखने और पेरलिन शोर समारोह बनाने का समय है। याद रखें कि ये केवल शोर समारोह के प्रक्षेपों के कुछ जोड़ हैं। इसलिए पेर्लिन का शोर केवल एक समारोह है। आप एक या अधिक पैरामीटर पास करते हैं, और यह एक संख्या के साथ प्रतिक्रिया करता है।
तो, यहाँ एक सरल 1-आयामी पेरलिन फ़ंक्शन है। पेर्लिन के कार्य का मुख्य भाग लूप है। लूप का प्रत्येक पुनरावृत्ति दूसरी आवृत्ति में एक और सप्तक जोड़ता है। प्रत्येक पुनरावृत्ति विभिन्न शोर कार्यों को बुलाती है, जिन्हें _{मैंने} शोर _i । अब आपको वास्तव में कई शोर कार्यों को लिखना होगा, प्रत्येक सप्तक के लिए, जैसा कि छद्म कोड में माना गया है। चूंकि सभी शोर फ़ंक्शन लगभग समान हैं, इन तीन बड़े अपराधों के अर्थ को छोड़कर, आप एक ही कोड रख सकते हैं, लेकिन बस प्रत्येक के लिए अलग-अलग सेट का उपयोग करें।

1-आयामी पर्लिन शोर (छद्म कोड)

  function Noise1(integer x) x = (x<<13) ^ x; return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0); end function function SmoothedNoise_1(float x) return Noise(x)/2 + Noise(x-1)/4 + Noise(x+1)/4 end function function InterpolatedNoise_1(float x) integer_X = int(x) fractional_X = x - integer_X v1 = SmoothedNoise1(integer_X) v2 = SmoothedNoise1(integer_X + 1) return Interpolate(v1 , v2 , fractional_X) end function function PerlinNoise_1D(float x) total = 0 p = persistence n = Number_Of_Octaves - 1 loop i from 0 to n frequency = 2i amplitude = pi total = total + InterpolatedNoisei(x * frequency) * amplitude end of i loop return total end function 

अब आप आसानी से 2 या अधिक आयामी पेरलिन शोर कार्यों को बनाने के लिए समान कोड लागू कर सकते हैं।

2-आयामी पेरलिन शोर (छद्म कोड)

 function Noise1(integer x, integer y) n = x + y * 57 n = (n<<13) ^ n; return ( 1.0 - ( (n * (n * n * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0); end function function SmoothNoise_1(float x, float y) corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16 sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8 center = Noise(x, y) / 4 return corners + sides + center end function function InterpolatedNoise_1(float x, float y) integer_X = int(x) fractional_X = x - integer_X integer_Y = int(y) fractional_Y = y - integer_Y v1 = SmoothedNoise1(integer_X, integer_Y) v2 = SmoothedNoise1(integer_X + 1, integer_Y) v3 = SmoothedNoise1(integer_X, integer_Y + 1) v4 = SmoothedNoise1(integer_X + 1, integer_Y + 1) i1 = Interpolate(v1 , v2 , fractional_X) i2 = Interpolate(v3 , v4 , fractional_X) return Interpolate(i1 , i2 , fractional_Y) end function function PerlinNoise_2D(float x, float y) total = 0 p = persistence n = Number_Of_Octaves - 1 loop i from 0 to n frequency = 2i amplitude = pi total = total + InterpolatedNoisei(x * frequency, y * frequency) * amplitude end of i loop return total end function 

मूल लेख के अंत में अतिरिक्त सामग्रियां हैं जिनके लिए यह दिलचस्प होगा; मुझे लगता है कि इसे खत्म करना मुश्किल नहीं होगा।

संदर्भ:
वास्तव में लेख ही ।
केन पेरलिन वेबसाइट

ps: प्रिय नाबालिगों, क्या यह पहले से ही माइनस को प्रेरित करने के लिए स्वीकार नहीं किया गया है?