छवि प्रसंस्करण मैट्रिक्स फ़िल्टर

यह लेख न केवल सबसे आम छवि प्रसंस्करण फिल्टर के बारे में बताता है, बल्कि एक समझदार रूप में उनके संचालन के लिए एल्गोरिदम का वर्णन करता है। लेख मुख्य रूप से इमेज प्रोसेसिंग में शामिल प्रोग्रामर के उद्देश्य से है।

कन्वेंशन मैट्रिक्स

कन्वेंशन मैट्रिक्स का उपयोग करके कई फिल्टर हैं, जिनमें से मुख्य नीचे वर्णित होंगे।

कन्वेंशन मैट्रिक्स गुणांक का एक मैट्रिक्स है जो वांछित परिणाम प्राप्त करने के लिए छवि पिक्सल के मूल्य से "गुणा" होता है।
निम्नलिखित एक दीक्षांत मैट्रिक्स अनुप्रयोग है:



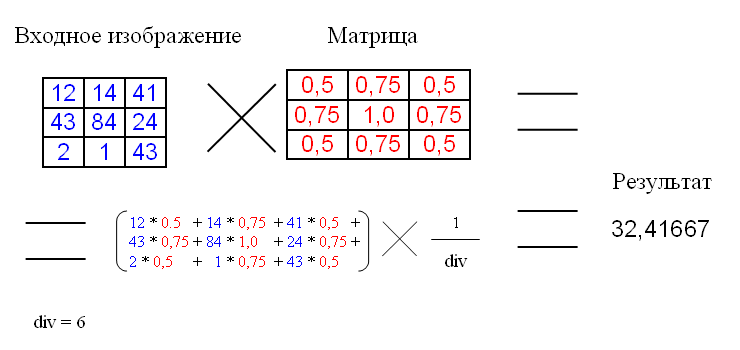
div एक सामान्यीकरण कारक है ताकि औसत तीव्रता अपरिवर्तित रहे।

उदाहरण में, मैट्रिक्स का आकार 3x3 है, हालांकि आकार बड़ा हो सकता है।

ब्लर फिल्टर

सबसे अधिक इस्तेमाल किया जाने वाला कनवल्शन मैट्रिक्स फ़िल्टर ब्लर फ़िल्टर है।

आमतौर पर मैट्रिक्स सामान्य (गाऊसी कानून) के अनुसार भरा जाता है। नीचे गॉसियन डिस्ट्रीब्यूशन के कानून के अनुसार 5x5 ब्लर मैट्रिक्स भरा हुआ है।



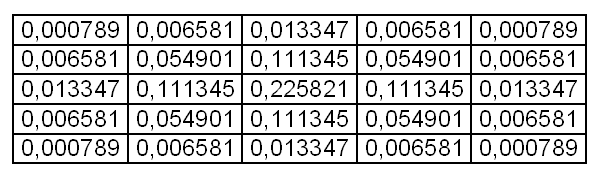
गुणांक पहले से ही सामान्यीकृत हैं, इसलिए इस मैट्रिक्स के लिए div एक है।

धब्बा की ताकत मैट्रिक्स के आकार पर निर्भर करती है।



यह सीमा की स्थितियों का उल्लेख करने योग्य है (यह समस्या सभी मैट्रिक्स फिल्टर के लिए प्रासंगिक है)। ऊपरी बाएँ पिक्सेल में इसके दाईं ओर "पड़ोसी" नहीं है, इसलिए, हमारे पास मैट्रिक्स गुणांक को गुणा करने के लिए कुछ भी नहीं है।



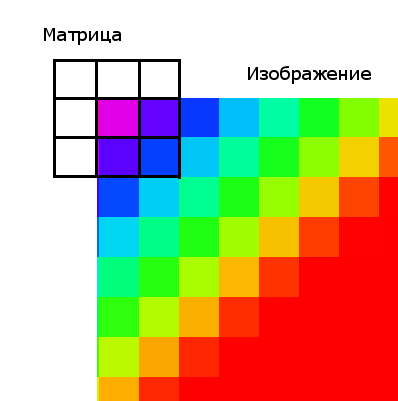
इस समस्या के 2 समाधान हैं:

1. फ़िल्टर को केवल उस छवि के "विंडो" पर लागू करना, जिसमें ऊपरी बाएँ कोने के निर्देशांक हैं [kernelSize / 2, kernelSize / 2], और निचले दाएं [चौड़ाई - kernelSize / 2, height - kernelSize / 2] के लिए। कर्नेलसाइज़ - मैट्रिक्स आकार; चौड़ाई, ऊंचाई - छवि का आकार।



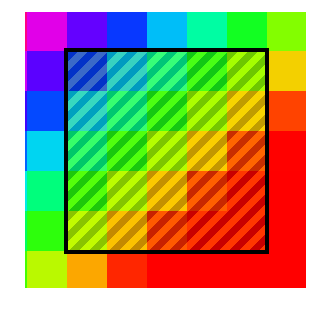
यह सबसे अच्छा तरीका नहीं है, क्योंकि फ़िल्टर पूरी छवि पर लागू नहीं होता है। यदि फ़िल्टर का आकार बड़ा है, उसी समय, गुणवत्ता बहुत अधिक होती है।

2. दूसरी विधि (जोड़) के लिए एक मध्यवर्ती छवि के निर्माण की आवश्यकता होती है। विचार आयाम (चौड़ाई + 2 * कर्नेलसाइज़ / 2, ऊंचाई + 2 * कर्नेलसाइज़ / 2) के साथ एक अस्थायी छवि बनाने के लिए है। इनपुट छवि को छवि के केंद्र में कॉपी किया जाता है, और किनारों को छवि के चरम पिक्सेल से भरा जाता है। ब्लर को मध्यवर्ती बफर पर लागू किया जाता है, और फिर परिणाम इसे से निकाला जाता है।



इस पद्धति की गुणवत्ता में कोई कमियां नहीं हैं, लेकिन अनावश्यक गणना करना आवश्यक है।

गाऊसी ब्लर फिल्टर में जटिलता ओ (हाय * वाई * एन * एन) है, जहां हाय, वाई छवि आकार हैं, एन मैट्रिक्स (फिल्टर कोर) का आकार है। इस एल्गोरिथ्म को स्वीकार्य गुणवत्ता के साथ अनुकूलित किया जा सकता है।

स्क्वायर कोर (मैट्रिक्स) को दो एक आयामी द्वारा प्रतिस्थापित किया जा सकता है: क्षैतिज और ऊर्ध्वाधर। कर्नेल आकार 5 के लिए, वे इस तरह दिखेंगे:



फ़िल्टर को 2 पास में लागू किया जाता है: परिणाम के लिए पहले क्षैतिज, और फिर ऊर्ध्वाधर (या प्रति क्रांति)।

इस एल्गोरिथ्म की जटिलता O (hi * wi * n) + O (hi * wi * n) = 2 * O (hi * wi * n) होगी, जो कि दो से अधिक कर्नेल आकार के लिए, एक वर्ग मैट्रिक्स के साथ पारंपरिक विधि की तुलना में तेज़ है।

स्पष्टता फिल्टर

स्पष्टता में सुधार के लिए, आपको निम्नलिखित मैट्रिक्स का उपयोग करना होगा:



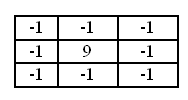
यह मैट्रिक्स सीमाओं पर मूल्यों में अंतर को बढ़ाता है। इस मैट्रिक्स के लिए div 1 है।



GIMP में एक "कनवल्शन मैट्रिक्स" फ़िल्टर है, जो आपके द्वारा आवश्यक मैट्रिक्स परिवर्तन की खोज को सरल करता है।



आप "मोड़ मैट्रिक्स के आधार पर ग्राफिक फ़िल्टर" लेख में कन्वेंशन मैट्रिक्स के आधार पर फ़िल्टर पर अधिक विस्तृत जानकारी पा सकते हैं।

मेडियन फिल्टर

एक माध्यिका फिल्टर आमतौर पर शोर को कम करने या एक छवि को "सुचारू" करने के लिए उपयोग किया जाता है।



फ़िल्टर विभिन्न आकारों के मैट्रीस के साथ काम करता है, लेकिन कन्वेक्शन मैट्रिक्स के विपरीत, मैट्रिक्स का आकार केवल प्रश्न में पिक्सेल की संख्या को प्रभावित करता है।

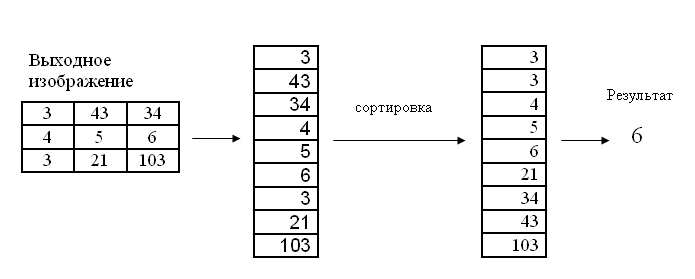
मंझला फिल्टर एल्गोरिथ्म इस प्रकार है:

वर्तमान पिक्सेल के लिए, मैट्रिक्स में "गिरने" वाले पिक्सेल को क्रमबद्ध किया जाता है, और औसत मान को क्रमबद्ध सरणी से चुना जाता है। यह मान वर्तमान पिक्सेल के लिए आउटपुट है।

नीचे तीन के मूल आकार के लिए माध्य फ़िल्टर है।

फिल्टर का कटाव और निर्माण

फ़िल्टर्स बिल्ड-अप और अपरदन क्रमशः रूपात्मक विस्तार या संकीर्णता प्राप्त करने के लिए उपयोग किया जाता है। सीधे शब्दों में कहें, छवियों के लिए, इसका मतलब है एक पड़ोस से अधिकतम या न्यूनतम तीव्रता वाला पिक्सेल चुनना।



बिल्डअप के परिणामस्वरूप, उज्ज्वल वस्तुओं में वृद्धि हुई है, और कटाव - अंधेरे वस्तुओं में वृद्धि।

फ़िल्टर एक इनपुट छवि और एक बाइनरी मैट्रिक्स का उपयोग करता है। बाइनरी मैट्रिक्स पड़ोस के आकार को निर्धारित करता है। आमतौर पर पड़ोस में एक गोल आकार होता है।



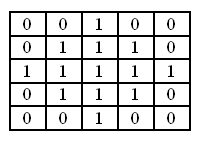
बिल्ड-अप फ़िल्टर का उपयोग चकाचौंध, उज्ज्वल प्रतिबिंबों को बढ़ाने के लिए किया जा सकता है।

निष्कर्ष

लेख ने कुछ इमेज प्रोसेसिंग फ़िल्टर का वर्णन किया, उनके एल्गोरिदम और एप्लिकेशन सुविधाओं का वर्णन किया।

ru.wikipedia.org/wiki/_
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/_
habrahabr.ru/post/43895