आपका दिन शुभ हो!
मैं आपके साथ शोर की उपस्थिति के साथ स्थानिक डेटा को क्लस्टर करने के लिए एक घनत्व एल्गोरिथ्म के MATLAB में कार्यान्वयन के साथ साझा करना चाहूंगा - डीबीएससीएएन (घनत्व आधारित स्थानिक क्लस्टरिंग ऑफ़ एप्लिकेशन विद नॉइज़)।

विशेषताएं

डीबीएससीएन एल्गोरिथ्म को 1996 में मार्टिन एस्टर, हंस-पीटर क्रिएगेल और उनके सहयोगियों द्वारा प्रस्तावित किया गया था, जो मनमाने रूप वाले समूहों में विभाजन (शुरू में स्थानिक) डेटा की समस्या के समाधान के रूप में थे। अधिकांश सपाट विभाजन एल्गोरिदम गोलाकार के करीब आकार बनाते हैं, क्योंकि वे दस्तावेजों की दूरी को क्लस्टर के केंद्र तक कम कर देते हैं। डीबीएससीएएन के लेखकों ने प्रयोगात्मक रूप से दिखाया कि उनका एल्गोरिथ्म विभिन्न आकृतियों के समूहों को पहचानने में सक्षम है।

मुख्य विचार

एल्गोरिथ्म में अंतर्निहित विचार यह है कि प्रत्येक क्लस्टर के भीतर बिंदुओं (वस्तुओं) का एक विशिष्ट घनत्व होता है, जो क्लस्टर के बाहर घनत्व की तुलना में काफी अधिक है, साथ ही साथ किसी भी क्लस्टर के घनत्व से कम शोर वाले क्षेत्रों में घनत्व है। अधिक सटीक रूप से, प्रत्येक क्लस्टर बिंदु के लिए, किसी दिए गए त्रिज्या के पड़ोस में कम से कम एक निश्चित संख्या में अंक होने चाहिए; इस अंक की संख्या एक सीमा मान द्वारा दी गई है। एल्गोरिथ्म की मूलभूत विशेषताओं की एक विस्तृत प्रस्तुति के लिए, कई परिभाषाओं को पेश करना आवश्यक है - आप 197-2007 के पृष्ठों पर उत्कृष्ट अध्ययन गाइड [1] में उनके साथ खुद को परिचित कर सकते हैं, जहां यह एल्गोरिथ्म सामान्य रूप में भी दिया गया है। मेरा सुझाव है कि आप अपना ध्यान सीधे लेखकों द्वारा प्रस्तावित विचारों के कार्यान्वयन पर दें।

इनपुट / आउटपुट जानकारी

इनपुट आयाम nx का एक कंट्रो मैट्रिक्स है। विचाराधीन बिंदुओं के निर्देशांक पहले दो कॉलम में स्थित हैं, अन्य दो कॉलम 0 से भरे हुए हैं।
एल्गोरिथ्म के परिणामस्वरूप, कॉन्टेस्ट मैट्रिक्स के कॉलम 3 और 4 भरे जाते हैं: 3 कॉलम कॉलम के बारे में जानकारी दर्शाता है कि क्या बिंदु संसाधित किया गया था; 4 कॉलम एक विशेष वर्ग से 1 से s-1 के लिए जिम्मेदार है। यदि -1 को 4 कॉलम में लिखा गया है, तो इस बिंदु को शोर के लिए जिम्मेदार ठहराया गया था।

MATLAB में कार्यान्वयन

n = length(cont(:,1)); %%    L_min = 30; %%    L = zeros(n,n); %%    Rez = zeros(n,1); %%    for i=1:1:n %%       < L_min   % L(:,i)=sqrt((cont(:,1)-cont(i,1)).^2 + (cont(:,2)-cont(i,2)).^2)<=L_min; %%       < L_min    % Rez(i) = sum(L(:,i))-1; L(:,i)=L(:,i).*(1:1:n)'; %%        < L_min    end kol=5; %%        < L_min    c=1; %%    for i=1:1:n if cont(i,3) == 0 %%      "" if Rez(i)<kol %%      < L_min,       cont(i,3)=1; %%   "" cont(i,4)=-1; %%    else %%      < L_min,     uvec = cont(:,4); %%        cont(i,4)=c; %%         while sum(uvec-cont(:,4))~=0 %%         uvec = cont(:,4); %%        for j=1:1:n %%     if cont(j,4)==c && cont(j,3)==0 %%          "" if Rez(j)<kol %%       L_min     kol cont(j,3)=1; %%    cont(j,4)=-1; %%    else %%  cont(j,3)=1; %%   "" cont(find(L(j,:)>0),4)=c; %%        L_min       end end; end; end; c=c+1; %%    end; else continue end; end; 

मैं MATLAB कोड के गलत हाइलाइटिंग के लिए माफी माँगता हूँ, और HABRAHABR पर इसका पता नहीं लगा सका।

काम के परिणाम

एल्गोरिथ्म के लिए प्रारंभिक जानकारी को 3 स्पष्ट रूप से प्रतिष्ठित समूहों के अलावा, बिंदुओं का एक समूह होना चाहिए, जिसमें शोर के लिए जिम्मेदार होना चाहिए।

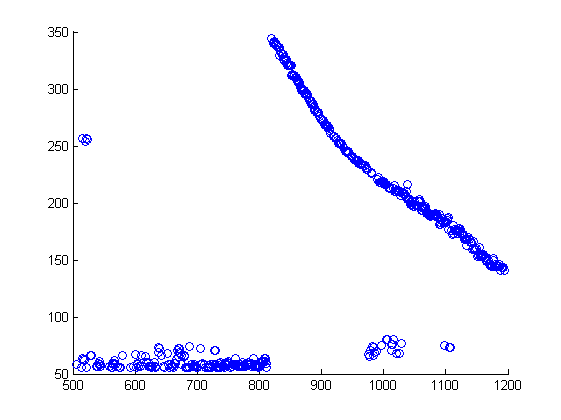
एल्गोरिथ्म के काम करने के बाद, हमें क्लस्टरिंग की निम्नलिखित तस्वीर मिलती है:

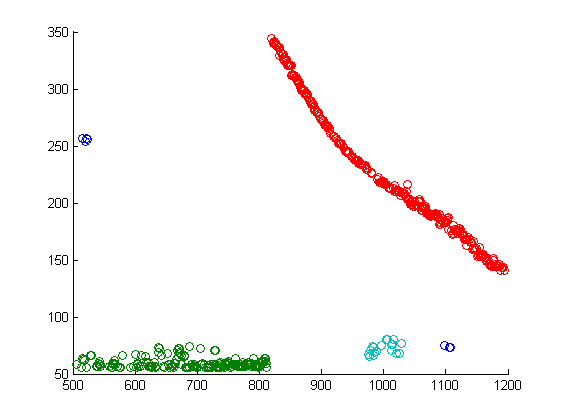
जैसा कि आप देख सकते हैं, एल्गोरिथ्म ने 3 समूहों और शोर (छवि में नीला बिखराव) की पहचान की, जिसकी उम्मीद की जानी थी! मैं इस तथ्य पर भी पाठक का ध्यान आकर्षित करना चाहूंगा कि एल्गोरिथ्म एक निश्चित वक्र के साथ स्थित बिंदुओं के चयन के कार्य से अच्छी तरह से जुड़ा हुआ है, जो उचित अनुप्रयोग के साथ, एक छवि में वस्तुओं के आकृति का चयन करने के कार्य के लिए इस एल्गोरिथ्म का उपयोग करता है, लेकिन यह एक पूरी तरह से अलग कहानी है!

साहित्य

प्राकृतिक भाषा और कंप्यूटर भाषा विज्ञान में ग्रंथों का स्वचालित प्रसंस्करण: पाठ्यपुस्तक। भत्ता / बोलशकोवा ई.आई., क्लेशिंस्की ई.एस., लांडे डी.वी., नोसकोव ए.ए., पेसकोवा ओ.वी., यागुनोवा ई.वी. - एम .: एमआईईएम, 2011 ।-- 272 पी।