हेलो, हैबर।
हाल ही में, यह सिर्फ इतना हुआ कि उन्होंने इस विषय पर अपनी पुरानी लिसेयुम में एक व्याख्यान दिया कि वे गणित क्यों पढ़ रहे हैं और बाद में इसके साथ क्या किया जा सकता है। 10 वीं कक्षा के स्कूली बच्चों के लिए, यह थोड़ा जटिल हो गया, शायद। मुझे आशा है कि यह विषय किसी व्यक्ति की हैब्रोसैक्विटी (यहां प्रस्तुत विकल्प से थोड़ा अधिक जटिल है, जो मैंने लिसेयुम में पढ़ा है, से दिलचस्प होगा, लेकिन मुझे नहीं लगता कि यह एक समस्या है)।
So. हम छवि प्रसंस्करण पर ध्यान केंद्रित करेंगे, विशेष रूप से, सबसे सरल, लेकिन एक वर्णनात्मक दृष्टिकोण से सुंदर, एक छवि में शोर को दबाने की विधि।
बहुत पहले नहीं मैंने खुद के लिए खोज की कि इमेज प्रोसेसिंग में कितना भौतिकी है। मुझे इसमें बहुत दिलचस्पी थी, क्योंकि विज्ञान की ये दो शाखाएँ कभी मेरे सिर के पार नहीं थीं। इस लेख में मैं प्रस्तुत करूंगा कि एक विमान पर बड़े पैमाने पर स्थानांतरण की समस्या को हल करके एक छवि से शोर को कैसे हटाया जा सकता है।
छवि देखें
सबसे पहले, हम स्पष्ट करते हैं कि हम एक छवि के रूप में क्या विचार करेंगे। विवरण की सादगी के लिए, अब हम केवल बी / डब्ल्यू आविष्कार पर विचार करेंगे।
हम उन्हें संतृप्ति के एक मैट्रिक्स के रूप में प्रतिनिधित्व करेंगे।

इस प्रकार, छवि में प्रत्येक पिक्सेल एक मैट्रिक्स तत्व से मेल खाती है। मैट्रिक्स में मान अंतराल से
float संख्या हैं
[0,255] ।
कुछ छवि ले लो और इसे करने के लिए शोर जोड़ें (यह शोर के साथ पहले से ही एक छवि की तलाश की तुलना में आसान है, क्योंकि आप जाँच सकते हैं कि एल्गोरिथ्म विभिन्न शोर तीव्रता को सेट करके शोर के साथ कितनी अच्छी तरह से मुकाबला करता है)। हमें ऐसा कुछ मिलता है:

एक समारोह के रूप में छवि
विधि की व्याख्या करने के लिए, मुझे कुछ संकेतन प्रस्तुत करने होंगे:
सबसे पहले, हम अपनी छवि को पिक्सेल निर्देशांक के एक कार्य के रूप में मानेंगे। इस प्रकार, यदि हम यह कहना चाहते हैं कि
और
निर्देशांक वाला पिक्सेल सफेद है, तो हम इसे
I(x,y)==255 रूप में लिख सकते हैं
इसके अलावा, यदि हमारे पास कोई फ़ंक्शन है, तो हम इससे व्युत्पन्न कर सकते हैं और फिर यह हमारे लिए काम में आएगा। चूंकि हमारे पास एक असतत फ़ंक्शन है, अर्थात, यह उन दोनों के बीच एक निर्दिष्ट कदम के साथ कोशिकाओं में परिभाषित किया गया है, हम इसे इस रूप में लिख सकते हैं (चूंकि फ़ंक्शन दो-आयामी है, फिर क्रमशः दो डेरिवेटिव हैं):
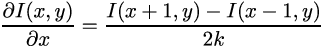
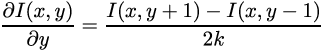
यहाँ
k==1 चूंकि आसन्न पिक्सेल = 1 पिक्सेल के बीच का अंतर है।
इस प्रकार, व्युत्पत्ति भी मूल छवि के समान आकार की होगी।


दोनों निर्देशांक के संबंध में व्युत्पन्न होने के बाद, ग्रेडिएंट की गणना करना तर्कसंगत है:
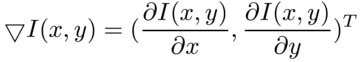
और इसका मूल्य:
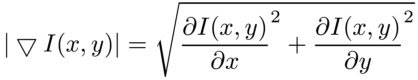
ढाल की भयावहता को एक छवि के रूप में प्रदर्शित किया जा सकता है:

अब, ढाल के परिमाण पर करीब से नज़र डालें। यह बहुत महत्व का है कि हमें जो जानकारी चाहिए वह संग्रहीत है।
शोर की छवि से छुटकारा पाने के लिए यह तर्कसंगत है कि इसे धुंधला करने की आवश्यकता है। हालांकि, धुंधलापन महत्वपूर्ण विवरण खो देता है। यही है, हम उन क्षेत्रों में धब्बा को सीमित करना चाहेंगे जहां ग्रेडिएंट काफी बड़ा है। सब यही रह गया कि यह कैसे किया जाए।
प्रसार प्रक्रिया के साथ कनेक्शन
यहाँ प्रसार की एक अद्भुत शारीरिक प्रक्रिया हमारी सहायता के लिए आती है। विमान में एक विशेष बिंदु पर द्रव्यमान की उपस्थिति के संकेतक के रूप में छवि मैट्रिक्स की कल्पना करें। प्रसार प्रक्रिया में तथ्य यह है कि द्रव्यमान "प्रसार" एक बड़े एकाग्रता के साथ एक छोटे से बिंदुओं के साथ बिंदुओं तक फैलता है। प्रसार की प्रक्रिया में, प्रवाह की अवधारणा है, जो तथाकथित फ़िक कानून का पालन करती है:

जहां
D डिफ्यूजन टेंसर है जो डिफ्यूजन की दिशा और परिमाण को परिभाषित करता है।
हम द्रव्यमान के संरक्षण के नियम भी लिखते हैं, जो कहता है कि आने वाले और बाहर जाने वाले प्रवाह के बीच का अंतर बिंदु पर द्रव्यमान में परिवर्तन के बराबर है:
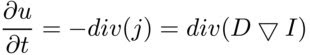
यदि प्रवाह सीमित नहीं है, अर्थात,
D==1 - द्रव्यमान सभी दिशाओं में समान रूप से फैल जाएगा, अर्थात, हमें गॉसियन कलंक के बराबर मिलेगा, जिसका अर्थ है कि हम महत्वपूर्ण छवि विवरण खो देंगे। हम एक ऐसी विधि में रुचि रखते हैं जिसके द्वारा प्रवाह को सीमित किया जा सके।
सबसे सरल तरीकों में से एक इसकी दिशा को प्रतिबंधित किए बिना प्रवाह की भयावहता को सीमित करना है। हम उसके बारे में आगे बात करेंगे।
आइए हम कुछ घटते हुए फलन को पेश करते हैं, जिसके इनपुट के साथ हम ढाल के परिमाण को प्रस्तुत करेंगे। इस स्तर पर यह कार्य एक विसरण टेंसर होगा:

फिर बड़े पैमाने पर संरक्षण समीकरण का रूप लेता है:

अगला, हम सभी सूत्र लिखेंगे (मैं शायद इस चरण को छोड़ दूंगा) और अंतिम समीकरण लिखूंगा जिसके साथ हम समस्या का समाधान पा सकते हैं:
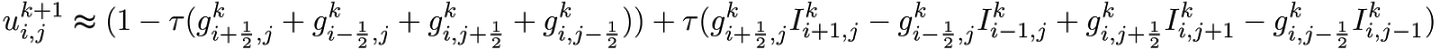
इस प्रकार, हमने एक पुनरावृत्ति योजना प्राप्त की, जो पैरामीटर मान
tau<=0.25 पर स्थिर है। यह बल्कि धीमा है, क्योंकि मूल विधि और अधिक सफल एल्गोरिदम इस पर आधारित हैं।
परिणाम
अंत में, हमें एक छवि मिलती है जो लगभग सभी महत्वपूर्ण विवरणों को बरकरार रखती है और लगभग सभी शोर खो देती है।
UPD: मैं ईमानदारी से माफी माँगता हूँ, छवियों को मिलाया गया था। छवि को बदल दिया, जो पहले था कि लेख में प्रस्तुत किए गए शोर के साथ छवि को संसाधित करने के परिणामस्वरूप क्या प्राप्त किया जाता है। मैं फिर से माफी मांगता हूं।

तुलना के लिए - मूल और शोर के साथ संस्करण (फिर से):


संदर्भ:
- पी। पेरोना, जे। मलिक: स्केल-स्पेस और एज डिटेक्शन ऐनिसोट्रोपिक डिफ्यूजन का उपयोग कर। आईईईई
पैटर्न विश्लेषण और मशीन इंटेलिजेंस 12 (7) पर लेनदेन: 629-639, 1990। - जे। विकर्ट: अनीसोट्रोपिक डिफ्यूजन इन इमेज प्रोसेसिंग। टेबनेर, स्टटगार्ट, 1998. पुस्तक है
अब उपलब्ध नहीं है, लेकिन जोचिम वेकर्ट की पीएचडी थीसिस, जो उनके आधार थी
पुस्तक, उसकी वेबसाइट पर उपलब्ध है। - टी। ब्रोक्स: लेक्चर ऑन कंप्यूटर विजन। फ़्रीबर्ग दुर्ग Breisgau, 2011
पुनश्च यदि आप गलतियाँ पाते हैं - तो मुझे आलोचना और सुझाव सुनने में खुशी होगी।