सभी को नमस्कार। इस हफ्ते, मशीन-लर्निंग कोर्स में, प्रोफेसर एंड्रयू एनजी ने प्रमुख घटक विधि के बारे में दर्शकों को बताया, जिसके साथ आप अपने डेटा के फीचर स्पेस के आयाम को कम कर सकते हैं। लेकिन दुर्भाग्य से, उन्होंने मैट्रिक्स के आइजेनवेक्टर और आइगेनवेल्यूज की गणना करने के तरीके के बारे में बात नहीं की, उन्होंने बस इतना कहा कि यह जटिल था और मैटलैब / ऑक्टेव फ़ंक्शन [USV] = svd (a) का उपयोग करने की सलाह दी।

मेरी परियोजना के लिए, मुझे c # में इस पद्धति के कार्यान्वयन की आवश्यकता थी, जो मैंने आज किया। मुख्य घटकों की विधि अपने आप में बहुत ही सुंदर और सुंदर है, और यदि आप गणित को नहीं समझते हैं जो इस सब के पीछे है, तो इसे शर्मिंदगी कहा जा सकता है। मैट्रिक्स के आइजनवेक्टरों की गणना के साथ समस्या यह है कि उनके सटीक मूल्यों की गणना करने का कोई त्वरित तरीका नहीं है, इसलिए आपको बाहर निकलना होगा। मैं इन तरीकों में से एक के बारे में बात करना चाहता हूं, और मैं इस प्रक्रिया को करने वाले सी # कोड भी दूंगा। मैं बिल्ली माँगता हूँ।

प्रमुख घटक विधि (अब तक कोड के बिना)

भाग एक: एल्गोरिथ्म का आरंभीकरण। इनपुट डेटा की एक सरणी है, साथ ही साथ अंतरिक्ष का आयाम जिसमें डेटा को कम करना होगा।

सहसंयोजक मैट्रिक्स की गणना की जाती है (इस मैट्रिक्स में एक अद्भुत संपत्ति है - यह सममित है, यह हमारे लिए बहुत उपयोगी है)
मैट्रिक्स के आइजनवेक्टरों की गणना की जाती है
Eigenvectors के पहले en को चुना गया है, जहाँ en एक ही आयाम है जिसके लिए फीचर स्पेस के आयाम को कम करना आवश्यक है; चयनित वैक्टर को लंबवत लिखा जा सकता है और एक मैट्रिक्स में इकट्ठा किया जा सकता है

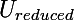
भाग दो: इनपुट वेक्टर के आयाम को कम करना। एक वेक्टर इनपुट को खिलाया जाता है, जैसा कि आरंभिक चरण में उपयोग किए गए डेटा सरणी में होता है; आउटपुट कम आयाम का एक वेक्टर है (या इनपुट के वेक्टर के प्रक्षेपण को एक स्वैच्छिक आधार पर eigenonctors का गठन किया जाता है)।

Eigenvectors के नमूने से सभी वैक्टर द्वारा स्केलरली इनपुट वेक्टर को गुणा करना, हम एक कम वेक्टर प्राप्त करते हैं:

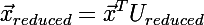
भाग तीन: एक वेक्टर के आयाम को बहाल करना (निश्चित रूप से जानकारी के नुकसान के साथ)। इनपुट आयाम के एक वेक्टर है जिसके बराबर हमने वैक्टर को कम किया ; आउटपुट मूल आयाम का एक वेक्टर है।

यदि आप मैट्रिक्स को स्थानांतरित करते हैं 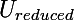फिर इसमें पिछले चरण में इनपुट वेक्टर के आयाम के रूप में कई लाइनें होंगी, और वांछित वेक्टर सूत्र द्वारा बहाल किया गया है: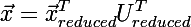

जैसा कि आप देख सकते हैं, सभी कम्प्यूटेशनल जटिलता प्रारंभिक चरण में है जब सहसंयोजक मैट्रिक्स और eigenvectors की गणना करते हैं। मैं सहसंयोजक मैट्रिक्स की गणना पर ध्यान केंद्रित नहीं करूंगा, क्योंकि यह परिभाषा के अनुसार भली प्रकार गणना की जाती है। मैट्रिक्स के आइजनवेक्टरों की गणना के लिए कई एल्गोरिदम का अध्ययन करने के बाद, मैं क्यूआर अपघटन की पुनरावृत्ति विधि पर बस गया। इसका एक महत्वपूर्ण प्रतिबंध है, यह केवल सममित मैट्रिक्स के लिए अधिक या कम सटीक परिणाम देता है, लेकिन हम भाग्यशाली हैं :), कोवरियस मैट्रिक्स सिर्फ इतना है। इस एल्गोरिथ्म की दूसरी सीमा यह है कि मैट्रिक्स पूर्ण-रैंक होना चाहिए।

क्यूआर अपघटन

Eigenvectors की खोज करने की पुनरावृत्ति QR विधि स्पष्ट रूप से QR अपघटन का उपयोग करती है, इसलिए पहले आपको इस प्रक्रिया को लागू करना होगा। इस प्रक्रिया को लागू करने के लिए, ग्राहम-श्मिट एल्गोरिथ्म को चुना गया था।

ऐसा करने के लिए, हमें एक फ़ंक्शन की आवश्यकता होती है जो वेक्टर के ऑन वेक्टर बी के प्रक्षेपण की गणना करता है:

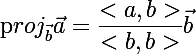
, जहां <> - वैक्टर के अदिश उत्पाद को निरूपित करते हैं।

public static double[] VectorProjection(double[] a, double[] b) { double k = ScalarVectorProduct(a, b)/ScalarVectorProduct(b, b); return ScalarToVectorProduct(k, b); }

मैं सरल कार्यों जैसे ScalarVectorProduct पर भी ध्यान केंद्रित नहीं करूंगा, ताकि पाठ में कोड का आकार महत्वपूर्ण मानदंड से अधिक न हो।

तो, वास्तविक QR अपघटन प्रक्रिया IList <double []> DecompositionGS (double [] [] a) एक मैट्रिक्स इनपुट प्राप्त करता है और प्रतिक्रिया में दो मैट्रिक्स देता है:

पहले इसके स्तंभों में एक अलंकारिक आधार होता है जैसे कि ;
दूसरा मैट्रिक्स ऊपरी त्रिकोणीय होगा ।

सबसे पहले, हम मैट्रिक्स को कॉलम में तोड़ते हैं और उन्हें एवी सूची में लिखते हैं:

 List<double[]> av = new List<double[]>(); foreach (double[] vector in DecomposeMatrixToColumnVectors(a)) { av.Add(vector); }

हम दो सहायक सूचियों को आरंभ करते हैं:

 List<double[]> u = new List<double[]>(); u.Add(av[0]); List<double[]> e = new List<double[]>(); e.Add(ScalarToVectorProduct(1 / NormOfVector(u[0]), u[0]));

ये एल्गोरिथम आरेख में उपयोग किए गए समान नाम की एक ही सूची हैं:

आरंभीकरण के बाद, पहले यू और ई की गणना की जाती है, हम लूप में निम्न मानों की गणना जारी रखते हैं:

 for (int i = 1; i < a.Length; i++) { double[] projAcc = new double[a.Length]; for (int j = 0; j < projAcc.Length; j++) { projAcc[j] = 0; } for (int j = 0; j < i; j++) { double[] proj = VectorProjection(av[i], e[j]); for (int k = 0; k < projAcc.Length; k++) { projAcc[k] += proj[k]; } } double[] ui = new double[a.Length]; for (int j = 0; j < ui.Length; j++) { ui[j] = a[j][i] - projAcc[j]; } u.Add(ui); e.Add(ScalarToVectorProduct(1/NormOfVector(u[i]), u[i])); }

और अंत में, हम आउटपुट फॉर्मेट में डेटा जेनरेट करते हैं:

 double[][] q = new double[a.Length][]; for (int i = 0; i < q.Length; i++) { q[i] = new double[a.Length]; for (int j = 0; j < q[i].Length; j++) { q[i][j] = e[j][i]; } } double[][] r = new double[a.Length][]; for (int i = 0; i < r.Length; i++) { r[i] = new double[a.Length]; for (int j = 0; j < r[i].Length; j++) { if (i >= j) { r[i][j] = ScalarVectorProduct(e[j], av[i]); } else { r[i][j] = 0; } } } r = Transpose(r); List<double[][]> res = new List<double[][]>(); res.Add(q); res.Add(r); return res;

हुर्रे! अब हमें इसके लिए एक परीक्षण की आवश्यकता है:

 [Test(Description = "Test of QRDecompositionGS")] public void QRDecompositionGSTest() { double[][] a = new double[][] { new double[] {12, -51, 4}, new double[] {6, 167, -68}, new double[] {-4, 24, -41} }; IList<double[][]> res = LinearAlgebra.QRDecompositionGS(a); double[][] expQ = new double[][] { new double[] {6.0/7, -69.0/175, -58.0/175}, new double[] {3.0/7, 158.0/175, 6.0/175}, new double[] {-2.0/7, 6.0/35, -33.0/35} }; double[][] expR = new double[][] { new double[] {14, 21, -14}, new double[] {0, 175, -70}, new double[] {0, 0, 35} }; Assert.True(Helper.AreEqualMatrices(expQ, res[0], 0.0001), "expQ != Q"); Assert.True(Helper.AreEqualMatrices(expR, res[1], 0.0001), "expR != R"); }

Helper.AreEqualMatrices फ़ंक्शन तत्व-वार मैट्रिसेस की तीसरे पैरामीटर तक तुलना करता है।

Iterative QR विधि

पुनरावृत्त QR विधि एक उल्लेखनीय प्रमेय पर आधारित है, जिसका सार यह है कि यदि आप मैट्रिक्स को शून्य के रूप में प्रारंभ करते हैं $formdata=\Large+A^{(0)}+=+A$ और निम्न प्रक्रिया को असीम रूप से कई बार दोहराएं:

$formdata=\Large+Q^{(k)}R^{(k)}+=+A^{(k-1)}$
$formdata=\Large+A^{(k)}+=+R^{(k)}Q^{(k)}$

और फिर सभी प्राप्त Qs को गुणा करें, परिणाम एक मैट्रिक्स है, जिसके कॉलम में मूल मैट्रिक्स के eigenvectors होंगे, जिनमें से मान अधिक सटीक होंगे, प्रक्रिया जितनी लंबी होगी। दूसरे शब्दों में, जैसा कि पुनरावृत्तियों की संख्या अनन्तता, उत्पाद को बताती है $formdata=\Large+\prod_{k=1}^{\infty}+Q^{(k)}$ eigenvectors के सटीक मूल्यों की ओर रुख करेंगे। उसी समय, उत्तरार्द्ध $formdata=\Large+A^{(k)}$ मुख्य विकर्ण पर मैट्रिक्स के eigenvalues होते हैं, लगभग निश्चित रूप से। मैं आपको याद दिलाता हूं कि यह एल्गोरिदम कम या ज्यादा सटीक रूप से केवल सममित मैट्रिक्स के लिए काम करता है।

तो, क्यूआर पुनरावृत्ति विधि IList <डबल [] []> EigenVectorValuesExtractionQRIterative (डबल [] [], डबल सटीकता, इंट मैक्सिमेटर) मैट्रिक्स के अतीत के इनपुट के रूप में कुछ मापदंडों को प्राप्त करता है।

दोहरी सटीकता - जिस सटीकता को हम प्राप्त करना चाहते हैं, एल्गोरिथ्म बंद हो जाएगा यदि आइजनवेक्टर के मूल्यों में परिवर्तन इस मूल्य से अधिक नहीं हैं;
int maxIterations - पुनरावृत्तियों की अधिकतम संख्या।

आउटपुट में हमें दो मैट्रिसेस मिलते हैं:

पहले इसके कॉलम में मैट्रिक्स के eigenvectors शामिल हैं a ;
इसके मुख्य विकर्ण पर दूसरी मैट्रिक्स में मैट्रिक्स के आइगेनवेल्यूज़ शामिल हैं a ।

इसलिए, हम एक एल्गोरिथ्म लिखना शुरू करेंगे, सबसे पहले हम ऐसे मैट्रिक्स बनाएँगे जिनमें मूल मैट्रिक्स के आइजनवेक्टर और ईजेनवेल्यूज़ होंगे:

 double[][] aItr = a; double[][] q = null;

और एल्गोरिथ्म के बंद होने तक लूप को चलाएं:

 for (int i = 0; i < maxIterations; i++) { IList<double[][]> qr = QRDecompositionGS(aItr); aItr = MatricesProduct(qr[1], qr[0]); if (q == null) { q = qr[0]; } else { double[][] qNew = MatricesProduct(q, qr[0]); bool accuracyAcheived = true; for (int n = 0; n < q.Length; n++) { for (int m = 0; m < q[n].Length; m++) { if (Math.Abs(Math.Abs(qNew[n][m]) - Math.Abs(q[n][m])) > accuracy) { accuracyAcheived = false; break; } } if (!accuracyAcheived) { break; } } q = qNew; if (accuracyAcheived) { break; } } }

उत्पादन उत्पन्न करें:

 List<double[][]> res = new List<double[][]>(); res.Add(q); res.Add(aItr); return res;

और निश्चित रूप से परीक्षण:

 [Test(Description = "Test of Eigen vectors extraction")] public void EigenVectorExtraction() { double[][] a = new double[][] { new double[] {1, 2, 4}, new double[] {2, 9, 8}, new double[] {4, 8, 2} }; IList<double[][]> ev = LinearAlgebra.EigenVectorValuesExtractionQRIterative(a, 0.001, 1000); double expEV00 = 15.2964; double expEV11 = 4.3487; double expEV22 = 1.0523; Assert.AreEqual(expEV00, Math.Round(Math.Abs(ev[1][0][0]), 4)); Assert.AreEqual(expEV11, Math.Round(Math.Abs(ev[1][1][1]), 4)); Assert.AreEqual(expEV22, Math.Round(Math.Abs(ev[1][2][2]), 4)); }

यह ध्यान देने योग्य है कि eigenvectors पुनरावृत्ति से दिशा में परिवर्तन कर सकते हैं, जिसे उनके निर्देशांक के संकेतों को बदलकर देखा जाएगा, लेकिन यह स्पष्ट है कि यह आवश्यक नहीं है।

प्रमुख घटक विधि का कार्यान्वयन

अब विषय के कार्यान्वयन के लिए सब कुछ तैयार है।

मॉडल (वर्ग) का छिपा हुआ पैरामीटर स्रोत से कोविरियन मैट्रिक्स के आइजनवेटर्स का सबसेट होगा:

 private IList<double[]> _eigenVectors = null;

डिजाइनर एक इनपुट डेटा सरणी और आयाम लेता है, जिसमें संकेतों की जगह, साथ ही साथ क्यूआर अपघटन के मापदंडों को कम करना आवश्यक है। अंदर, सहसंयोजक मैट्रिक्स की गणना की जाती है और पहले कुछ eigenvectors लिए जाते हैं। सामान्य तौर पर, वांछित सूचना हानि पैरामीटर के लिए आइजनवेक्टरों की इष्टतम संख्या चुनने का एक तरीका है, अर्थात्। किस आयाम पर आप अंतरिक्ष को कम कर सकते हैं, जानकारी के एक निश्चित प्रतिशत से अधिक नहीं खो रहा है, लेकिन मैं इस कदम को छोड़ देता हूं, आप पाठ्यक्रम वेबसाइट पर एंड्रयू एनजी द्वारा व्याख्यान में इसके बारे में सुन सकते हैं।

 internal DimensionalityReductionPCA(IList<double[]> dataSet, double accuracyQR, int maxIterationQR, int componentsNumber) { double[][] cov = BasicStatFunctions.CovarianceMatrixOfData(dataSet); IList<double[][]> eigen = LinearAlgebra.EigenVectorValuesExtractionQRIterative(cov, accuracyQR, maxIterationQR); IList<double[]> eigenVectors = LinearAlgebra.DecomposeMatrixToColumnVectors(eigen[0]); if (componentsNumber > eigenVectors.Count) { throw new ArgumentException("componentsNumber > eigenVectors.Count"); } _eigenVectors = new List<double[]>(); for (int i = 0; i < componentsNumber; i++) { _eigenVectors.Add(eigenVectors[i]); } }

फिर हम लेख की शुरुआत से सूत्रों द्वारा प्रत्यक्ष और व्युत्क्रम परिवर्तन को लागू करते हैं।

 public double[] Transform(double[] dataItem) { if (_eigenVectors[0].Length != dataItem.Length) { throw new ArgumentException("_eigenVectors[0].Length != dataItem.Length"); } double[] res = new double[_eigenVectors.Count]; for (int i = 0; i < _eigenVectors.Count; i++) { res[i] = 0; for (int j = 0; j < dataItem.Length; j++) { res[i] += _eigenVectors[i][j]*dataItem[j]; } } return res; } public double[] Reconstruct(double[] transformedDataItem) { if (_eigenVectors.Count != transformedDataItem.Length) { throw new ArgumentException("_eigenVectors.Count != transformedDataItem.Length"); } double[] res = new double[_eigenVectors[0].Length]; for (int i = 0; i < res.Length; i++) { res[i] = 0; for (int j = 0; j < _eigenVectors.Count; j++) { res[i] += _eigenVectors[j][i]*transformedDataItem[j]; } } return res; }

परीक्षण

परीक्षण के लिए, हम एक छोटे डेटा ऐरे के साथ आएंगे, और मैटलैब पर मूल्यों की जाँच करेंगे (पीसीए = पर घर से कोड का उपयोग करके), हम परीक्षण के लिए एक क्लास लिखेंगे:

 [TestFixture(Description = "Test of DimensionalityReductionPCA")] public class DimensionalityReductionPCATest { private IList<double[]> _data = null; private IDataTransformation<double[]> _transformation = null; private double[] _v = null; [SetUp] public void SetUp() { _v = new double[] { 1, 0, 3 }; _data = new List<double[]>() { new double[] {1, 2, 23}, new double[] {-3, 17, 5}, new double[] {13, -6, 7}, new double[] {7, 8, -9} }; _transformation = new DimensionalityReductionPCA(_data, 0.0001, 1000, 2); } [Test(Description = "Test of DimensionalityReductionPCA transform")] public void DimensionalityReductionPCATransformTest() { double[] reduced = _transformation.Transform(_v); double[] expReduced = new double[] {-2.75008, 0.19959}; Assert.IsTrue(Helper.AreEqualVectors(expReduced, reduced, 0.001)); double[] reconstructed = _transformation.Reconstruct(reduced); double[] expReconstructed = new double[] {-0.21218, -0.87852, 2.60499}; Assert.IsTrue(Helper.AreEqualVectors(expReconstructed, reconstructed, 0.001)); }

संदर्भ

मशीन लर्निंग कोर्स
लेख जो एक पुनरावृत्त QR विधि का वर्णन करता है
लेख के पाठ में विकिपीडिया लिंक का एक गुच्छा

C # में प्रमुख घटक विधि का कार्यान्वयन