एक सरल हफ़मैन पाठ स्ट्रिंग एन्कोडिंग उदाहरण

आपने शायद डेविड हफमैन और उनके लोकप्रिय संपीड़न एल्गोरिथ्म के बारे में सुना है। यदि नहीं, तो मेरा सुझाव है कि आप स्वयं इंटरनेट खोजें - इस लेख में मैं आपको इतिहास या गणित के पाठों से नहीं रोकूंगा। मैं आपको अभ्यास में यह दिखाने की कोशिश करूंगा कि इस एल्गोरिदम को टेक्स्ट स्ट्रिंग पर कैसे लागू किया जाए। हमारा आवेदन केवल दर्ज किए गए स्ट्रिंग से वर्णों के लिए कोड मान उत्पन्न करेगा और इससे प्रस्तुत कोड से मूल स्ट्रिंग को फिर से बनाएगा।

हफ़मैन कोडिंग का विचार एक स्ट्रिंग में वर्णों के उपयोग की आवृत्ति का उपयोग करने पर आधारित है। सबसे अधिक बार सामना किए जाने वाले चरित्र को सबसे कम संभव कोड मान दिया जाना चाहिए, और कम से कम अक्सर सामना किए गए चरित्र को यथासंभव लंबे समय तक दिया जाना चाहिए। इस तथ्य के कारण कि सबसे अधिक बार होने वाले पात्रों को संग्रहीत करने के दौरान पहले की तुलना में कम जगह लेनी चाहिए, और कम से कम अक्सर सामना किए गए वर्ण अधिक स्थान ले सकते हैं - चूंकि उनमें से कुछ हैं, इसलिए यह परिणाम को बहुत प्रभावित नहीं करेगा।

हमारे उदाहरण के लिए, मैंने चरित्र को 8-बिट बनाने का फैसला किया, अर्थात। प्रकार चार। उसी सफलता के साथ, सोलह, दस या बीस बिट्स की लंबाई चुनना संभव था। अपेक्षित इनपुट डेटा के आधार पर प्रतीक की लंबाई का चयन किया जाना चाहिए। उदाहरण के लिए, वीडियो फ़ाइलों को एन्कोड करने के लिए, मैं पिक्सेल के समान आकार का एक चरित्र चुनूंगा। ध्यान रखें कि किसी चरित्र की लंबाई बढ़ने या घटने से प्रत्येक वर्ण के लिए कोड की लंबाई प्रभावित होती है - आखिरकार, जितनी लंबी लंबाई, इस लंबाई के अधिक वर्ण मौजूद हो सकते हैं: सोलह की तुलना में आठ बिट्स में लिखने और शून्य करने के बहुत कम तरीके हैं। इसलिए, कार्य के आधार पर प्रतीक की लंबाई को समायोजित किया जाना चाहिए।

हफ़मैन एल्गोरिथ्म प्राथमिकता के साथ सक्रिय रूप से द्विआधारी पेड़ों और कतारों का उपयोग करता है, इसलिए यदि आप उनसे परिचित नहीं हैं, तो आपको पहले ज्ञान अंतराल में भरना होगा।

मान लीजिए कि हमारे पास "बीप बोप बीयर!" लाइन है, जो स्मृति में 15 * 8 = 120 बिट्स लेती है। हफ़मैन एन्कोडिंग के बाद, इस आकार को 40 बिट तक कम किया जा सकता है। यदि आप विवरण के साथ गलती पाते हैं, तो हम स्क्रीन पर स्ट्रिंग (टाइपोस और जीरो) के 40 तत्वों से युक्त एक स्ट्रिंग प्रदर्शित करेंगे, और मेमोरी में लगभग 40 बिट्स पर कब्जा करने के लिए, इस स्ट्रिंग को बाइनरी अंकगणितीय संचालन का उपयोग करके बिट्स में परिवर्तित किया जाना चाहिए, जो हम यहां नहीं होंगे विस्तार से विचार करें।

तो, लाइन "बीप बोप बीयर!" पर विचार करें। उनकी आवृत्ति के आधार पर सभी तत्वों के लिए कोड मानों का निर्माण करने के लिए, आपको एक बाइनरी ट्री बनाने की आवश्यकता होती है जिसमें प्रत्येक शीट में किसी दिए गए स्ट्रिंग से एक चरित्र होता है। हम पेड़ को पत्तियों से जड़ तक बनाएंगे, ताकि कम आवृत्ति वाले तत्व जड़ से दूर हों, और अधिक लगातार इसके करीब होते हैं। आपको जल्द ही पता चल जाएगा कि क्यों।

इस तरह के एक पेड़ का निर्माण करने के लिए, हम प्राथमिकता कतार का उपयोग करेंगे, लेकिन थोड़ा संशोधित - प्राथमिकताओं को उलट दें ताकि सबसे कम प्राथमिकता वाला तत्व सबसे महत्वपूर्ण हो। यह पता चला है कि कतार पहले तत्वों को सबसे कम आवृत्ति के साथ वापस करेगी। यह संशोधन हमें पत्तियों से शुरू होने वाले पेड़ के निर्माण में मदद करेगा।

सबसे पहले, आइए प्रत्येक वर्ण की आवृत्ति की गणना करें:

प्रतीक	आवृत्ति
'बी'	3
'ई'	4
'पी'	2
''	2
'O'	2
'आर'	1
'!'	1

उसके बाद, हम प्रत्येक प्रतीक के लिए द्विआधारी वृक्ष तत्व बनाएंगे और उन्हें एक प्राथमिकता कतार के रूप में प्रतिनिधित्व करेंगे, जिसके लिए हम आवृत्ति का उपयोग करेंगे।


अब कतार से पहले दो तत्वों को लें और एक तीसरा बनाएं जो उनके माता-पिता होंगे। हम इस नए तत्व को एक प्राथमिकता के साथ एक कतार में रखते हैं, जो इसके दो वंशजों की प्राथमिकताओं के योग के बराबर है। दूसरे शब्दों में, उनकी आवृत्तियों के योग के बराबर।


अगला, हम पिछले एक के समान चरणों को दोहराएंगे:





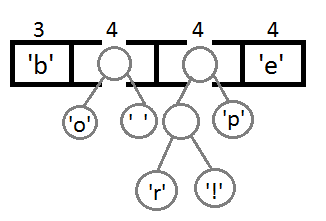
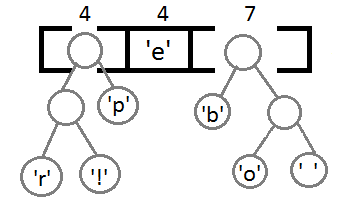
अब, अपने नए माता-पिता का उपयोग करके अंतिम दो तत्वों के संयोजन के बाद, हमें परिणामी बाइनरी ट्री मिलता है:


यह प्रत्येक वर्ण को उसके कोड को असाइन करने के लिए रहता है ऐसा करने के लिए, हम गहराई से चलना शुरू करते हैं और हर बार, सही सबट्री पर विचार करते हुए, हम इसे कोड 1 में लिखेंगे, और बाएं सबट्री पर विचार करेंगे - 0।


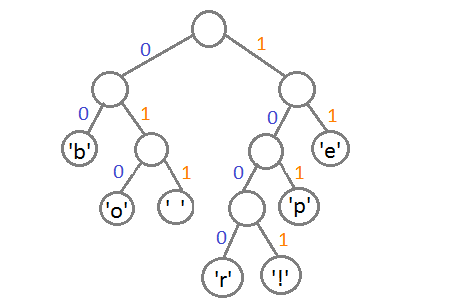
परिणामस्वरूप, कोड मानों के लिए अक्षरों का पत्राचार इस प्रकार है:

चारसेट मूल्य	कोड मान
'बी'	00
'ई'	11
'पी'	101
''	011
'O'	010
'आर'	1000
'!'	1001

बिट्स के एक क्रम को डिकोड करना बहुत सरल है: आपको पेड़ को पीछे हटाने की जरूरत है, अगर एक पाया जाता है तो बाएं सबट्री को छोड़ देना चाहिए और यदि यह 0. है, तो यह आवश्यक है कि जब तक हम एक पत्ती न मिलें, तब तक ट्रैवर्सिंग जारी रखें। एन्कोडेड वर्ण का वांछित मान। उदाहरण के लिए, एन्कोडेड लाइन "101 11 101 11" और हमारे डिकोडिंग ट्री लाइन "पेपे" से मेल खाती है।

यहां यह ध्यान रखना महत्वपूर्ण है कि कोई भी कोड मूल्य किसी अन्य का उपसर्ग नहीं है। हमारे उदाहरण में, 00 वर्ण कोड "b" है। इसका मतलब यह है कि 000 अब किसी अन्य वर्ण के लिए कोड नहीं हो सकता है, क्योंकि अन्यथा यह डिकोडिंग में संघर्ष का कारण होगा। आखिरकार, अगर 00 से गुजरने के बाद, हम "बी" शीट पर आए, तो 000 के कोड मूल्य से हमें अब कोई अन्य चरित्र नहीं मिलेगा।

व्यवहार में, हफ़मैन पेड़ को उत्पन्न करने के बाद, आपको हफ़मैन तालिका का निर्माण करने की भी आवश्यकता है। एक तालिका (एक लिंक की गई सूची या एक सरणी के रूप में) एन्कोडिंग प्रक्रिया को और अधिक कुशल बना देगी, क्योंकि एक पेड़ में एक चरित्र की खोज करने के लिए अनुचित समय लेने वाली है और साथ ही साथ अपना कोड लिखती है। चूँकि हम यह नहीं जानते कि यह प्रतीक कहाँ स्थित है, इसलिए सबसे खराब स्थिति में, हमें इसकी खोज में पूरे वृक्ष को छाँटना होगा। आमतौर पर, एक हफ़मैन तालिका का उपयोग एन्कोडिंग के लिए किया जाता है, और एक हफ़मैन का पेड़ डिकोडिंग के लिए उपयोग किया जाता है।

इनपुट लाइन: बीप बोप बीयर!
बाइनरी इनपुट स्ट्रिंग: 0110 0010 0110 0101 0101 0111 0000 0000 0000 0110 0010 0110 1111 0110 1111 0111 0000 0000 0010 0110 0110 0110 0101 01111 00111 0010 0001
कोडेड स्ट्रिंग: 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001

एक स्ट्रिंग के ASCII एन्कोडिंग और हफ़मैन कोड में इसकी उपस्थिति के बीच एक महत्वपूर्ण अंतर नोटिस करना आसान है।

यह ध्यान दिया जाना चाहिए कि लेख केवल एल्गोरिथ्म के सिद्धांत की व्याख्या करता है। व्यावहारिक उपयोग के लिए, आपको एन्कोडेड अनुक्रम की शुरुआत या अंत में हफ़मैन पेड़ जोड़ना होगा। संदेश के प्राप्तकर्ता को पता होना चाहिए कि पेड़ को सामग्री से कैसे अलग किया जाए और इसे पाठ दृश्य से कैसे पुनर्स्थापित किया जाए। ऐसा करने का एक अच्छा तरीका किसी पूर्व-चयनित क्रम में पेड़ को पीछे हटाना है, जो प्रत्येक शीट के लिए 0 के नीचे लिख रहा है जो एक शीट नहीं है, और प्रत्येक शीट के लिए 1 है। यूनिट के बाद, आप मूल चरित्र लिख सकते हैं (हमारे मामले में, ASCII एन्कोडिंग में char, 8 बिट्स टाइप करें)। इस रूप में लिखे गए पेड़ को एन्कोड किए गए अनुक्रम की शुरुआत में रखा जा सकता है - फिर प्राप्तकर्ता, जिसने पेड़ को पार्सिंग की शुरुआत में बनाया है, पहले से ही पता चल जाएगा कि नीचे रिकॉर्ड किए गए संदेश को कैसे डिकोड किया जाए और इससे मूल प्राप्त करें।

आप " Adaptive Huffman कोडिंग " लेख में एल्गोरिथ्म के एक और अधिक उन्नत संस्करण के बारे में पढ़ सकते हैं।

पीएस (अनुवादक से)
उनके लेख ब्लॉग में मूल लेख से जोड़ने के लिए धन्यवाद बॉबूक ।