🔃 🧔🏽 📅 C # में k- साधन एल्गोरिथ्म का कार्यान्वयन (एक सामान्यीकृत मीट्रिक के साथ) 👨🏽‍💼 👼🏽 👩🏿‍🤝‍👨🏾

सभी को नमस्कार। मशीन सीखने पर पाठ्यक्रम में बताने के लिए एंड्रयू एनजी के पास क्या समय नहीं था, इस विषय को जारी रखते हुए, मैं k- साधन एल्गोरिथ्म के मेरे कार्यान्वयन का एक उदाहरण दूंगा। मेरा कार्य क्लस्टरिंग एल्गोरिदम को लागू करना था, लेकिन मुझे मूल्यों के बीच सहसंबंध की डिग्री को ध्यान में रखना था। मैंने मीट्रिक के रूप में महालनोबिस दूरी का उपयोग करने का फैसला किया, मैं ध्यान देता हूं कि क्लस्टरिंग के लिए डेटा का आकार इतना बड़ा नहीं है, और डिस्क को क्लस्टर करने के लिए कैश करने की कोई आवश्यकता नहीं थी। कार्यान्वयन के लिए, मैं बिल्ली के लिए पूछता हूं।

समस्या

शुरू करने के लिए, आइए विचार करें कि समस्या क्या है, क्यों न केवल यूक्लिडियन दूरी को किसी अन्य मीट्रिक के साथ बदल दिया जाए। दो मापदंडों k- साधन एल्गोरिथ्म के लिए इनपुट हैं: क्लस्टरिंग के लिए डेटा और क्लस्टर की संख्या जिसमें डेटा को विभाजित किया जाना चाहिए। एल्गोरिथ्म में निम्नलिखित चरण होते हैं।

किसी तरह से क्लस्टर सेंट्रोइड्स की प्रारंभिक आरंभीकरण (उदाहरण के लिए, आप उस स्थान से यादृच्छिक रूप से चयनित बिंदुओं द्वारा प्रारंभिक मान सेट कर सकते हैं जिसमें डेटा परिभाषित किया गया है; आप इनपुट डेटा सरणी, आदि से यादृच्छिक बिंदुओं का चयन कर सकते हैं)।
ई-स्टेप ( अपेक्षा ): डेटा तत्वों और समूहों के बीच एक जुड़ाव होता है, जो उनके केंद्रों (केन्द्रक) के रूप में दर्शाया जाता है।
एम-स्टेप ( अधिकतमकरण ): क्लस्टर के केंद्रों को डेटा से औसत मान के रूप में पुनर्गठित किया जाता है जो संबंधित क्लस्टर (या, दूसरे शब्दों में, मॉडल मापदंडों को इस तरह से संशोधित किया जाता है कि चयनित क्लस्टर में होने वाले तत्व की संभावना को अधिकतम करने के लिए)। यदि चरण 2 के बाद क्लस्टर खाली हो गया है, तो किसी अन्य तरीके से पुनर्निवेशीकरण होता है।
अभिसरण तक दोहराए गए चरण 2-3 को दोहराया जाता है, या जब तक एल्गोरिथ्म को रोकने के लिए एक और मानदंड तक नहीं पहुंच जाता है (उदाहरण के लिए, यदि पुनरावृत्तियों की एक निश्चित संख्या पार हो जाती है)।

इस सरल एल्गोरिथ्म के पीछे के गणित को समझने के लिए, मैं आपको बायेसियन क्लस्टरिंग और उम्मीद-अधिकतमकरण एल्गोरिदम पर लेख पढ़ने की सलाह देता हूं।

यूक्लिडियन दूरी को किसी अन्य मीट्रिक द्वारा प्रतिस्थापित करने की समस्या एम-स्टेप है। उदाहरण के लिए, यदि हमारे पास पाठात्मक डेटा है और लेवेंसहाइट दूरी का उपयोग मीट्रिक के रूप में किया जाता है, तो औसत मान प्राप्त करना पूरी तरह से तुच्छ कार्य नहीं है। मेरे लिए, यहां तक कि महालनोबिस के लिए औसत ढूंढना भी जल्दी हल होने वाली समस्या नहीं थी, लेकिन मैं भाग्यशाली था और एक लेख आया जिसमें "सेंट्रोइड" का चयन करने का एक बहुत ही सरल तरीका बताया गया था, और मुझे अपने दिमाग को महालनोबिस के औसत मूल्य पर रैक करने की आवश्यकता नहीं थी। उद्धरण चिह्नों में, क्योंकि केन्द्रक का सटीक मान नहीं खोजा जाता है, लेकिन इसका अनुमानित मूल्य चुना जाता है, जिसे उस लेख में क्लस्टरॉइड कहा जाता है (या, के -मेडोइड्स के साथ सादृश्य द्वारा , इसे एक हनीओड कहा जा सकता है)। इस प्रकार, अधिकतमकरण कदम को निम्नलिखित एल्गोरिथ्म द्वारा बदल दिया जाता है।

एम-चरण: उन सभी डेटा तत्वों के बीच जो सेंट्रोइड को सौंपा गया था, वह तत्व चुना गया है जिसके लिए क्लस्टर के अन्य सभी तत्वों के लिए दूरी का योग न्यूनतम है; यह तत्व क्लस्टर का नया केंद्र बन जाता है।

वैसे, मेरे लिए अभिसरण का प्रश्न अभी भी खुला है, लेकिन कुछ उप-अपनाने के समाधान पर एल्गोरिथ्म को रोकने के कई तरीके हैं। इस कार्यान्वयन में, हम एल्गोरिथ्म को रोक देंगे यदि लागत फ़ंक्शन बढ़ना शुरू हो जाता है।

वर्तमान विभाजन के लिए लागत सूत्र निम्न सूत्र का उपयोग करेगा:

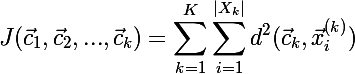
जहां K समूहों की संख्या है,

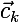
- क्लस्टर का वर्तमान केंद्र,

क्या क्लस्टर k, और के लिए दिए गए तत्वों का समूह है

क्लस्टर k का ith तत्व है।

औसत दूरी की खोज के लिए, यह ध्यान देने योग्य है कि यदि मीट्रिक फ़ंक्शन निरंतर और अलग-अलग है, तो ग्रेडिएंट की खोज के लिए ढाल वंश एल्गोरिथ्म का उपयोग किया जा सकता है, जो निम्न लागत फ़ंक्शन को कम करता है:

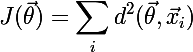
जहां x वर्तमान क्लस्टर को दिए गए तत्व हैं। मैं अगले लेख में इस विकल्प पर विचार करने की योजना बना रहा हूं, लेकिन अब कार्यान्वयन में हम इस बात पर ध्यान देंगे कि जल्द ही कुछ मीट्रिक के लिए कुछ मीट्रिक / क्लस्टरॉयड खोज विधि जोड़ी जाएगी।

मैट्रिक्स

पहले, आइए मीट्रिक का एक सामान्य दृश्य बनाएं और फिर सामान्य तर्क और कई मेट्रिक्स के ठोस कार्यान्वयन को लागू करें।

public interface IMetrics<T> { double Calculate(T[] v1, T[] v2); T[] GetCentroid(IList<T[]> data); }

इस प्रकार, मीट्रिक डेटा प्रकार से सारगर्भित है और हम इसे संख्यात्मक वैक्टर और लाइनों और वाक्यों के बीच लेवेनशेटिन दूरी के बीच यूक्लिडियन दूरी के रूप में लागू कर सकते हैं।

अब हम मेट्रिक्स के लिए एक बेस क्लास बनाएंगे जिसमें हम ऊपर वर्णित सरल विधि द्वारा क्लस्टरॉयड सर्च फंक्शन को लागू करते हैं।

 public abstract class MetricsBase<T> : IMetrics<T> { public abstract double Calculate(T[] v1, T[] v2); public virtual T[] GetCentroid(IList<T[]> data) { if (data == null) { throw new ArgumentException("Data is null"); } if (data.Count == 0) { throw new ArgumentException("Data is empty"); } double[][] dist = new double[data.Count][]; for (int i = 0; i < data.Count - 1; i++) { dist[i] = new double[data.Count]; for (int j = i; j < data.Count; j++) { if (i == j) { dist[i][j] = 0; } else { dist[i][j] = Math.Pow(Calculate(data[i], data[j]), 2); if (dist[j] == null) { dist[j] = new double[data.Count]; } dist[j][i] = dist[i][j]; } } } double minSum = Double.PositiveInfinity; int bestIdx = -1; for (int i = 0; i < data.Count; i++) { double dSum = 0; for (int j = 0; j < data.Count; j++) { dSum += dist[i][j]; } if (dSum < minSum) { minSum = dSum; bestIdx = i; } } return data[bestIdx]; } }

गेटकॉन्स्टायर विधि में, हम एक ऐसे तत्व की तलाश करते हैं जिसके लिए शेष डेटा तत्वों के लिए वर्ग दूरी का योग न्यूनतम हो। सबसे पहले, हम एक सममित मैट्रिक्स बनाते हैं जिसमें तत्वों में संबंधित डेटा तत्वों के बीच की दूरी होती है। मैट्रिक्स के गुणों का उपयोग करना: d (x, x) = 0 और d (x, y) = d (y, x), हम सुरक्षित रूप से शून्य के साथ विकर्ण को भर सकते हैं और मुख्य विकर्ण के साथ मैट्रिक्स को प्रतिबिंबित कर सकते हैं। फिर हम लाइनों पर योग करते हैं और न्यूनतम मूल्य की तलाश करते हैं।

उदाहरण के लिए, चलिए महालनोबिस और यूक्लिड की दूरियों का कार्यान्वयन बनाते हैं।

 internal class MahalanobisDistanse : MetricsBase<double> { private double[][] _covMatrixInv = null; internal MahalanobisDistanse(double[][] covMatrix, bool isInversed) { if (!isInversed) { _covMatrixInv = LinearAlgebra.InverseMatrixGJ(covMatrix); } else { _covMatrixInv = covMatrix; } } public override double Calculate(double[] v1, double[] v2) { if (v1.Length != v2.Length) { throw new ArgumentException("Vectors dimensions are not same"); } if (v1.Length == 0 || v2.Length == 0) { throw new ArgumentException("Vector dimension can't be 0"); } if (v1.Length != _covMatrixInv.Length) { throw new ArgumentException("CovMatrix and vectors have different size"); } double[] delta = new double[v1.Length]; for (int i = 0; i < v1.Length; i++) { delta[i] = v1[i] - v2[i]; } double[] deltaS = new double[v1.Length]; for (int i = 0; i < deltaS.Length; i++) { deltaS[i] = 0; for (int j = 0; j < v1.Length; j++) { deltaS[i] += delta[j]*_covMatrixInv[j][i]; } } double d = 0; for (int i = 0; i < v1.Length; i++) { d += deltaS[i]*delta[i]; } d = Math.Sqrt(d); return d; } }

जैसा कि आप कोड से देख सकते हैं, गेटकॉस्टेरॉइड विधि को ओवरराइड नहीं किया गया है, हालांकि अगले लेख में मैं इस पद्धति को ढाल वंश एल्गोरिथ्म का उपयोग करके ओवरराइड करने की कोशिश करूंगा।

 internal class EuclideanDistance : MetricsBase<double> { internal EuclideanDistance() { } #region IMetrics Members public override double Calculate(double[] v1, double[] v2) { if (v1.Length != v2.Length) { throw new ArgumentException("Vectors dimensions are not same"); } if (v1.Length == 0 || v2.Length == 0) { throw new ArgumentException("Vector dimension can't be 0"); } double d = 0; for (int i = 0; i < v1.Length; i++) { d += (v1[i] - v2[i]) * (v1[i] - v2[i]); } return Math.Sqrt(d); } public override double[] GetCentroid(IList<double[]> data) { if (data.Count == 0) { throw new ArgumentException("Data is empty"); } double[] mean = new double[data.First().Length]; for (int i = 0; i < mean.Length; i++) { mean[i] = 0; } foreach (double[] item in data) { for (int i = 0; i < item.Length; i++) { mean[i] += item[i]; } } for (int i = 0; i < mean.Length; i++) { mean[i] = mean[i]/data.Count; } return mean; } #endregion }

यूक्लिडियन दूरी के कार्यान्वयन में, गेट्सोएरॉइड विधि को ओवरराइड किया जाता है, और सटीक सेंट्रोइड मूल्य की तलाश करता है: प्रत्येक समन्वय के औसत मूल्यों की गणना की जाती है।

क्लस्टरिंग

चलो क्लस्टरिंग एल्गोरिदम के कार्यान्वयन के लिए आगे बढ़ते हैं। फिर, पहले क्लस्टरिंग एल्गोरिदम के लिए एक इंटरफ़ेस बनाएं।

 public interface IClusterization<T> { ClusterizationResult<T> MakeClusterization(IList<DataItem<T>> data); }

जहां क्लस्टरिंग का परिणाम निम्नानुसार है:

 public class ClusterizationResult<T> { public IList<T[]> Centroids { get; set; } public IDictionary<T[], IList<DataItem<T>>> Clusterization { get; set; } public double Cost { get; set; } }

और डेटा तत्व वर्ग:

 public class DataItem<T> { private T[] _input = null; private T[] _output = null; public DataItem(T[] input, T[] output) { _input = input; _output = output; } public T[] Input { get { return _input; } } public T[] Output { get { return _output; } set { _output = value; } } }

हम केवल इनपुट संपत्ति में रुचि रखते हैं, क्योंकि यह एक शिक्षक रहित प्रशिक्षण है।

उपरोक्त इंटरफेस का उपयोग करते हुए k- साधन एल्गोरिथ्म के कार्यान्वयन के लिए आगे बढ़ते हैं।

 internal class KMeans : IClusterization<double>

निम्नलिखित डेटा क्लस्टरिंग एल्गोरिथ्म में इनपुट है (मैंने अपने कोड को थोड़ा सा काट दिया ताकि शुरुआती सेंट्रोइड्स को कैसे शुरू किया जाए, इसके साथ परेशान न करें, हम यादृच्छिक बिंदु आरंभीकरण का उपयोग करेंगे, हम इसे यहां बर्दाश्त कर सकते हैं, क्योंकि हम

IClusterization):
clusterCount - IMetrics metrics -

संख्यात्मक डेटा का क्लस्टरिंग कर रहे हैं

IClusterization):
clusterCount - IMetrics metrics -

IClusterization):
clusterCount - IMetrics metrics -

IClusterization): clusterCount - IMetrics metrics -
IClusterization): clusterCount - IMetrics metrics -

C # में k- साधन एल्गोरिथ्म का कार्यान्वयन (एक सामान्यीकृत मीट्रिक के साथ)

समस्या

मैट्रिक्स

क्लस्टरिंग

More articles: