कम्प्यूटेशनल ज्यामिति, या मैं ओलंपियाड प्रोग्रामिंग में कैसे शामिल हो गया। भाग 1

नमस्ते, प्रिय हभ्रवचन! यह मेरा दूसरा लेख है, और मैं कम्प्यूटेशनल ज्यामिति के बारे में बात करना चाहूंगा।

थोड़ा इतिहास

मैं गणित के संकाय में पहले से ही 4 वें वर्ष का छात्र हूं, और इससे पहले कि मैंने प्रोग्रामिंग शुरू की, मैंने खुद को 100 प्रतिशत गणितज्ञ माना।

पहले वर्ष के अंत में, कंप्यूटर विज्ञान में मेरे शिक्षक, जो ओलंपियाड प्रोग्रामिंग में लगे हुए हैं, ने मेरा ध्यान आकर्षित किया। उनके पास प्रति टीम केवल एक गणितज्ञ की कमी थी। इसलिए धीरे-धीरे वे मुझे ओलंपियाड प्रोग्रामिंग के आदी होने लगे। सच कहूँ तो, मेरे लिए यह बहुत मुश्किल था: पहले साल में डेल्फी शब्द सीखने वाले व्यक्ति के लिए। हालांकि, मेरे शिक्षक एक बहुत ही सक्षम विशेषज्ञ बन गए और मुझे एक अच्छा दृष्टिकोण मिला। उन्होंने मुझे गणितीय समस्याएं देनी शुरू कर दीं, जिन्हें मैंने पहली बार गणितीय रूप से हल किया, और उसके बाद ही कोड लिखा (आधे में एक पाप के साथ)।

मुझे वास्तव में अपने शिक्षक का दृष्टिकोण पसंद है: "इस विषय से निपटें, और फिर हमें बताएं, ताकि हम सभी समझ सकें।"

इसलिए, पहला महत्वपूर्ण कार्य जिसे मैंने निपटने के लिए सौंपा था वह था कम्प्यूटेशनल ज्यामिति, कंप्यूटर विज्ञान के इस खंड के विशिष्ट कार्यों को समझना आवश्यक था। और मैंने सभी जिम्मेदारी के साथ इस कार्य को करने का निर्णय लिया।

मुझे याद है कि कब तक मुझे इन कामों को झेलना पड़ा, ताकि वे सभी परीक्षाओं को सूचना विज्ञान की वेबसाइट पर कर दें। लेकिन अब मुझे बहुत खुशी है कि मैं सभी परीक्षणों से गुजरा और मुझे पता है कि कम्प्यूटेशनल ज्यामिति की समस्याएं क्या हैं।

प्रविष्टि

“कम्प्यूटेशनल ज्यामिति कंप्यूटर विज्ञान की एक शाखा है जो ज्यामितीय समस्याओं को हल करने के लिए एल्गोरिदम का अध्ययन करती है। ऐसी समस्याएँ कंप्यूटर ग्राफिक्स, इंटीग्रेटेड सर्किट, तकनीकी उपकरणों आदि के डिज़ाइन में उत्पन्न होती हैं। ऐसी समस्याओं का प्रारंभिक डेटा कई बिंदुओं, सेगमेंट, पॉलीगॉन, आदि का सेट हो सकता है। परिणाम या तो किसी प्रश्न का उत्तर हो सकता है, या किसी ज्यामितीय वस्तु का। "

चूंकि लेख काफी बड़ा है, इसलिए मैंने इसे दो भागों में तोड़ने का फैसला किया: पहला भाग पॉलीगॉन को समर्पित है, दूसरा विभिन्न ज्यामितीय वस्तुओं की सापेक्ष स्थिति के लिए।

वैक्टर के बारे में थोड़ा सिद्धांत

एक सेगमेंट जिसके लिए यह इंगित किया जाता है कि इसके किन सिरों को शुरुआत माना जाता है और जो अंत है, उसे वेक्टर कहा जाता है। अंतरिक्ष के किसी भी बिंदु को वेक्टर के रूप में भी माना जा सकता है। ऐसे वेक्टर को शून्य कहा जाता है। शून्य वेक्टर की शुरुआत और अंत मेल खाता है, और इसकी कोई विशेष दिशा नहीं है।


एक नॉनजरो वेक्टर एबी की लंबाई खंड एबी की लंबाई है। शून्य वेक्टर की लंबाई शून्य के बराबर मानी जाती है।
यदि वे एक ही रेखा पर या समानांतर रेखा पर झूठ बोलते हैं, तो दो नॉनज़रो वैक्टर को कोलिनियर कहा जाता है। यदि दो नॉनज़ेरो वैक्टर एबी और सीडी आपस में मिलते हैं और यदि किरणें एबी और सीडी कोडेड हैं, तो वैक्टर एबी और सीडी को कोडायरेक्शनल कहा जाता है, और यदि ये किरणें कोडायरेक्शनल नहीं हैं, तो वैक्टर एबी और सीडी को विपरीत रूप से निर्देशित कहा जाता है। शून्य वेक्टर को किसी भी वेक्टर के साथ संरेखित माना जाता है।

वैक्टर का स्केलर उत्पाद

वैक्टर का स्केलर उत्पाद उनके बीच के कोण के कोसाइन द्वारा इन वैक्टर की लंबाई के उत्पाद के बराबर एक संख्या है।
(a, b) = | a || b | cos a (a, b)

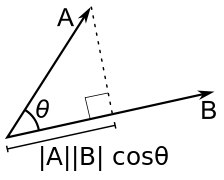
यदि वैक्टर उनके निर्देशांक a (x ₁ , y ₁ ), b (x ₂ , y ₂ ) द्वारा दिए गए हैं तो स्केलर उत्पाद (a, b) = x ₁ x ₂ + y ₁ y ₂ ।

वैक्टर का ओब्लिक उत्पाद

विमान में वैक्टरों के छद्मकोशिका या तिरछे उत्पाद को संख्या कहा जाता है
[a, b] = | a || b | sin =
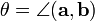
जहाँ - ए से बी तक रोटेशन (वामावर्त) का कोण। यदि वैक्टर और बी में से कम से कम एक शून्य है, तो [ए, बी] = 0 डाल दें।
यदि वैक्टर उनके निर्देशांक (x ₁ , y ₁ ), b (x ₂ , y ₂ ) द्वारा दिए जाते हैं तो तिरछा उत्पाद [a, b] = x ₁ y ₂ - x ₂ y ₁ ।
वैक्टर के ज्यामितीय तिरछे उत्पाद इन वैक्टर द्वारा फैलाए गए समांतर चतुर्भुज का उन्मुख क्षेत्र है।


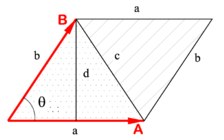
कम्प्यूटेशनल ज्यामिति समस्याओं में वैक्टर के तिरछा उत्पाद कोम्बिनेटरिक्स में पुनरावृत्ति के समान सम्मान की जगह लेता है। यह कम्प्यूटेशनल ज्यामिति का एक प्रकार का मोती है। कम्प्यूटेशनल ज्यामिति में लगभग हर समस्या में ललाट समाधान के बजाय तिरछा उत्पाद का उपयोग करने का एक सरल समाधान है।

अब अभ्यास करते हैं

आइए त्रिकोणों के साथ शुरू करते हैं

टास्क नंबर 1

कार्य बहुत सरल है, अर्थात्: तीन संख्याओं का उपयोग करके, बी, सी दर्ज किया गया है, यह निर्धारित करें कि क्या ऐसे पक्षों के साथ एक त्रिकोण मौजूद है।

निर्णय
यह स्पष्ट है कि यहां हमें केवल त्रिकोण असमानता की जांच करने की आवश्यकता है: a + b> c, a + c> b, b + b> a। दिलचस्प है, जब त्रिकोण असमानता का अध्ययन करते हैं, केवल मेरे पास एक सवाल था: क्या नकारात्मक संख्याएं भी इन तीन असमानताओं को संतुष्ट कर सकती हैं? बाहर मुड़ता है नहीं! यदि हम प्रत्येक असमानता को जोड़ते हैं, तो हम एक> 0, b> 0, c> 0. प्राप्त करते हैं, इसलिए, त्रिकोण के अस्तित्व के लिए त्रिकोण असमानता एक आवश्यक और पर्याप्त स्थिति है।

टास्क नंबर 2

यह कार्य पिछले वाले के समान है जिसमें त्रिकोण पक्षों द्वारा परिभाषित नहीं किया गया है, लेकिन कोने के निर्देशांक द्वारा।

निर्णय
पहली नज़र में, समाधान स्पष्ट लगता है: त्रिकोण के पक्षों की गणना करें और पिछले एक को समस्या को कम करें। हालाँकि, दो बिंदुओं A (x ₁ , y ₁ ), B (x ₂ , y ₂ ) के बीच की दूरी की गणना सूत्र between (x ₁ -x ₂ ) ² + (y ₁ -y ₂ ) ^{2 से की जाती है,} जड़ का नुकसान संभव है सटीकता, जो त्रिकोण असमानता की जाँच के लिए खराब है। यह पता चला है कि यदि त्रिभुज को उसके सिरों के निर्देशांक द्वारा परिभाषित किया जाता है, तो उसके पक्षों की लंबाई की गणना करना और त्रिकोण की असमानता की जांच करना आवश्यक नहीं है। इस स्थिति में, एक त्रिभुज मौजूद नहीं होता है और केवल अगर ये तीन बिंदु एक सीधी रेखा पर स्थित होते हैं। और यह आसानी से वैक्टर के एक परोक्ष उत्पाद के माध्यम से सत्यापित है। यदि यह शून्य के बराबर है, तो वेक्टर्स को मिलाया जाता है, अर्थात, तीनों बिंदु एक सीधी रेखा पर स्थित होते हैं।


निम्नलिखित सभी समस्याओं में, हम मानते हैं कि एक त्रिकोण मौजूद है, क्योंकि हमने सिर्फ एक त्रिकोण के अस्तित्व की जांच करने के लिए प्रक्रिया की जांच की।

टास्क नंबर 3

त्रिभुज अपने पक्षों द्वारा निर्धारित किया जाता है। त्रिकोण के प्रकार को निर्धारित करें: obtuse, आयताकार या तीव्र-कोण।

निर्णय
याद रखें कि प्रत्येक प्रकार का त्रिभुज क्या है।



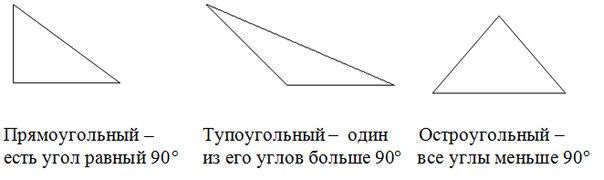
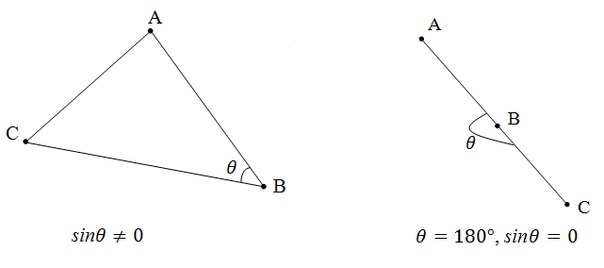
ज्यामिति के पाठ्यक्रम से, यह ज्ञात है कि विपरीत दिशा में एक बड़ा कोण है (हमें इसकी आवश्यकता है)। इसलिए, यदि हमें पता चलता है कि बड़ा कोण क्या है, तो हम त्रिकोण के प्रकार को समझेंगे:

1. 90 ° से अधिक कोण - त्रिभुज का तिरछा होना
2. कोण 90 ° से कम - तीव्र-कोण त्रिभुज
3. कोण 90 ° है - त्रिभुज आयताकार है

हम कोसाइन प्रमेय का उपयोग करते हैं:


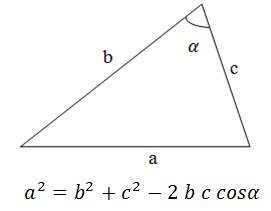
जाहिर है, यदि किसी कोण का कोसाइन शून्य से अधिक है, तो कोण 90 ° से कम है, यदि यह शून्य है, तो कोण 90 ° है, यदि यह शून्य से कम है, तो कोण 90 ° से अधिक है। हालांकि, थोड़ा प्रतिबिंब के बाद, आप समझ सकते हैं कि कोण के कोसाइन की गणना करना आवश्यक नहीं है, आपको केवल इस संकेत को ध्यान में रखना होगा:

• यदि cosα> 0, तो ² <b ² + c ² एक तीव्र-कोण त्रिकोण है
• यदि cosα = 0 है, तो एक ² = b ² + c ² एक सही त्रिकोण है
• यदि cosα <0 है, तो एक ² > b ² + c ² एक प्रसूति त्रिकोण है

जहां एक बड़ा पक्ष है।

टास्क नंबर 4

कार्य पिछले कार्य के समान है, केवल त्रिभुज अपने पक्षों से नहीं, बल्कि कोने के निर्देशांक द्वारा निर्धारित किया जाता है।

निर्णय
समस्या 2 के समान, हम कह सकते हैं कि यह कार्य पिछले कार्य (जिस तरह से है) से पूरी तरह से कम हो गया है। हालांकि, दूसरी समस्या के रूप में, समाधान को सरल बनाया जा सकता है। सामान्य तौर पर, यदि किसी त्रिभुज को उसके शीर्षों के निर्देशांक द्वारा परिभाषित किया जाता है, तो पक्षों की गणना करने की तुलना में वैक्टर के माध्यम से इसके साथ काम करना हमेशा आसान होता है। पिछले कार्य के समान, यह निर्धारित करना आवश्यक है कि त्रिकोण के कोणों में सबसे बड़ा कौन सा है। कोणों का प्रकार आसानी से इसे बनाने वाले वैक्टर के स्केलर उत्पाद के संकेत द्वारा निर्धारित किया जाता है: यह एक तीव्र कोण के लिए सकारात्मक है, एक सही कोण के लिए शून्य और एक अप्रिय कोण के लिए नकारात्मक है। इसलिए, सभी तीन स्केलर उत्पादों को गिनना और उन्हें गुणा करना आवश्यक है और इस संख्या के संकेत से आप त्रिकोण के प्रकार का न्याय कर सकते हैं।

टास्क नंबर 5

दिए गए पक्षों द्वारा त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

निर्णय
स्पष्ट समाधान हेरोन सूत्र को लागू करना है।

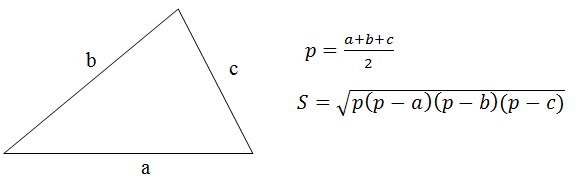
वैसे, इस सूत्र के प्रमाण में किसी की दिलचस्पी नहीं थी?

टास्क नंबर 6

त्रिभुज के क्षेत्र की गणना उसके कोने के निर्देशांक द्वारा दी गई है।

निर्णय
हम समाधान के बारे में बात नहीं करेंगे, जो पिछली समस्या को कम करता है, लेकिन ब्रैड उत्पाद के ज्यामितीय अर्थ का उपयोग करने की कोशिश करता है। दो वैक्टरों का ज्यामितीय तिरछा उत्पाद इन वैक्टरों पर फैला हुआ समांतर चतुर्भुज के उन्मुख क्षेत्र को परिभाषित करता है। चूंकि एक समांतरभुज का विकर्ण इसे दो समान त्रिभुजों में विभाजित करता है, इसलिए हम अपने त्रिभुज के क्षेत्रफल को समांतर चतुर्भुज के आधे क्षेत्र के रूप में पा सकते हैं।
वैक्टर a (x ₁ , y ₁ ), b (x ₂ , y ₂ ) के लिए

त्रिकोण का S = (x ₁ y ₂ - x ₂ y ₁ ) / 2 - उन्मुख क्षेत्र

टास्क नंबर 7

एक बिंदु और उसके त्रिकोण के निर्देशांक द्वारा दिए गए त्रिकोण को देखते हुए। निर्धारित करें कि बिंदु इस सीमा के अंदर, सीमा पर या उसके बाहर स्थित है या नहीं।

निर्णय
इस कार्य के दो मौलिक समाधान हैं। कम से कम आकर्षक के साथ शुरू करते हैं।

क्षेत्र विधि

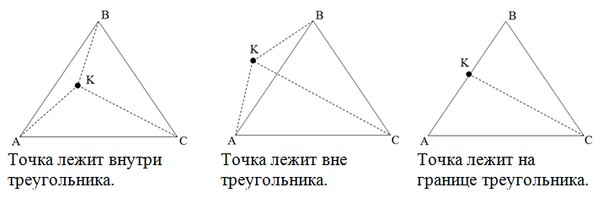
यदि त्रिभुज AKB, AKC, BKC के क्षेत्रों का योग (उन्मुख नहीं है, लेकिन "साधारण") त्रिभुज ABC के क्षेत्र से बड़ा है, तो बिंदु त्रिभुज के बाहर स्थित है। यदि पहले तीन क्षेत्रों का योग चौथे के बराबर है, तो आपको यह जांचने की आवश्यकता है कि क्या तीन क्षेत्रों में से एक शून्य के बराबर है। यदि बराबर है, तो बिंदु त्रिकोण की सीमा पर स्थित है, अन्यथा अंदर।
स्वाभाविक रूप से, वैक्टर के तिरछे उत्पाद के माध्यम से त्रिकोण के क्षेत्र की गणना करना आवश्यक है। यह तरीका बहुत अच्छा नहीं है। चूंकि फ्लोटिंग पॉइंट तुलनाओं का उपयोग यहां किया जाता है, जिसके कारण तुलना करते समय गलत निर्णय लिया जा सकता है। दूसरी विधि, फिर से, वैक्टर पर आधारित है, यह सभी मामलों में बहुत अधिक प्रभावी है।

आधा विमान की जाँच

यदि त्रिभुज के कम से कम एक हिस्से में "स्प्रेड" होता है, तो इसके विपरीत और बिंदु अलग-अलग आधे विमानों के साथ होता है, तो बिंदु त्रिकोण के बाहर स्थित होता है। अन्यथा, यदि बिंदु त्रिभुज की भुजाओं वाली कम से कम एक रेखा का है, तो यह त्रिभुज की सीमा पर है। अन्यथा, बिंदु त्रिकोण के अंदर स्थित है।

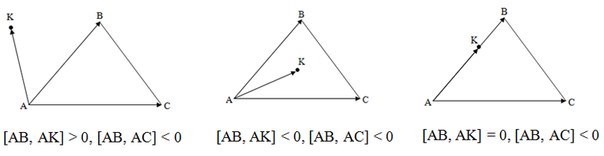
पहले उदाहरण में, पक्ष AB ने शीर्ष C और बिंदु K को अलग-अलग आधे विमानों में विभाजित किया है, इसलिए बिंदु बाहर स्थित है।

टास्क नंबर 8

एक बहुभुज के क्षेत्र की गणना जो इसके कोने के निर्देशांक द्वारा दी गई है।

निर्णय
बहुभुज से हमारा तात्पर्य एक साधारण बहुभुज से है, जो कि आत्म-चौराहे के बिना है। इसके अलावा, यह या तो उत्तल या गैर-उत्तल हो सकता है।

इस समस्या को दो तरीकों से हल किया जा सकता है: ट्रेपोज़िड्स और त्रिकोण के उन्मुख क्षेत्रों की गणना करके।

ट्रेपेज़ॉइड विधि

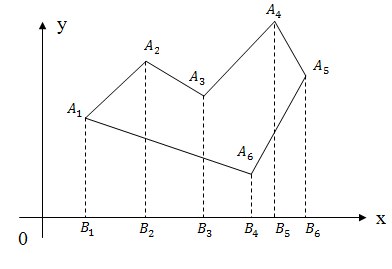
बहुभुज के क्षेत्र की गणना करने के लिए, इसे ट्रेपोज़िड्स में विभाजित करना आवश्यक है, क्योंकि यह आंकड़ा में दिखाया गया है, और फिर परिणामी ट्रेपोज़िड्स के उन्मुख क्षेत्रों को जोड़ते हैं, यह मूल बहुभुज का उन्मुख क्षेत्र होगा।
S = S _{A 1 A 2 B 2 B 1} + S _{A 2 A 3 B 3 B 2} + S _{A 3 A 4 B 4 B 5 B 3} + S _{A 4 A 5 B 6 B 5} + S _{A 5 A 6 B 4 B 6} + एस _{ए 6 ए 1 बी 1 बी 4 4}
हम अच्छी तरह से ज्ञात सूत्र के अनुसार ट्रेपेज़ियम के क्षेत्र पर विचार करते हैं: एक ऊंचाई तक आधार का आधा योग
S _{A 1 A 2 B 2 B 1} = 0.5 * (A ₁ B ₁ + A ₂ B ₂ ) * (B ₂ - B ₁ )

चूंकि परिणामी क्षेत्र उन्मुख है, इसलिए इसके मापांक की गणना करना आवश्यक है।

त्रिकोण विधि

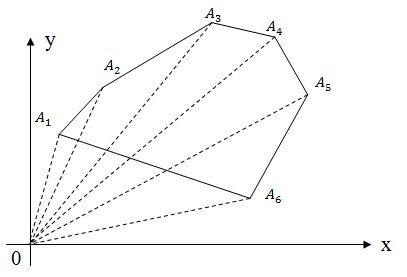
पिछली पद्धति के समान, बहुभुज को ट्रेपोज़ॉइड में नहीं, बल्कि त्रिकोण में विभाजित करना संभव है, जैसा कि आंकड़े में दिखाया गया है। परिणामस्वरूप, इन त्रिभुजों के उन्मुख क्षेत्रों को जोड़ते हुए, हम फिर से बहुभुज के उन्मुख क्षेत्र को प्राप्त करते हैं।
S = S _{O A 1 A 2} + S _{O A 2 A 3} + S _{O A 3 A 4} + S _{O A 4 A 5} + S _{O A 5 A 6} + S _{O A 6 A 1}

जैसा कि आप देख सकते हैं, बहुभुज के क्षेत्र की गणना करने का कार्य काफी सरल है। मुझे नहीं पता कि क्यों, लेकिन मैं इस समस्या को ट्रेपोज़ॉइड द्वारा विभाजित करके हल करना पसंद करता हूं (शायद इसलिए कि मैंने इसे सभी ओलिंपियाड्स पर इस तरह हल किया)। इसके अलावा, दूसरे समाधान में, तिरछे क्षेत्र की गणना तिरछे उत्पाद के माध्यम से की जानी चाहिए। बगुले का फार्मूला भूल जाना चाहिए !!!

टास्क नंबर 9

बहुभुज अपने अनुगामी के क्रम में इसके कोने के निर्देशांक द्वारा दिया जाता है। यह जांचना आवश्यक है कि क्या बहुभुज उत्तल है।

निर्णय
आपको याद दिला दूं कि एक बहुभुज को उत्तल कहा जाता है यदि यह किसी आधे रेखा में किसी भी रेखा के संबंध में होता है।


समस्या फिर से वैक्टर के तिरछे उत्पाद की गणना करने के लिए कम हो जाती है, अर्थात्, उत्तल बहुभुज के लिए, तिरछी उत्पादों के संकेत [ए _I A _{+ i + 1} , A _{i + 1} A _{i + 2} ] सकारात्मक या नकारात्मक होते हैं। इसलिए, यदि हम गोल की दिशा जानते हैं, तो उत्तल बहुभुज के लिए तिरछा उत्पादों का संकेत समान है: यह वामावर्त के चारों ओर जाने पर गैर-नकारात्मक है और दक्षिणावर्त घूमने पर सकारात्मक नहीं है।

टास्क नंबर 10

विमान पर एक बहुभुज (आवश्यक रूप से उत्तल नहीं) इसके कोने के निर्देशांक द्वारा दिया जाता है। इसके अंदर स्थित पूर्णांक निर्देशांक के साथ अंकों की संख्या को गिनना आवश्यक है (लेकिन इसकी सीमा पर नहीं)।

निर्णय
इस समस्या को हल करने के लिए, हम एक सहायक समस्या पर विचार करते हैं: खंड इसके सिरों के निर्देशांक द्वारा दिया जाता है, जो पूर्णांक होते हैं। खंड पर झूठ बोलने वाले पूर्णांक बिंदुओं की संख्या की गणना करना आवश्यक है। यह स्पष्ट है कि यदि खंड ऊर्ध्वाधर या क्षैतिज है, तो सिरों के निर्देशांक को घटाना और एक को जोड़ना आवश्यक है। ब्याज के मामले में जब खंड ऊर्ध्वाधर या क्षैतिज नहीं है। यह इस मामले में पता चला है कि यह एक समकोण त्रिभुज के खंड को पूरा करने के लिए आवश्यक है और इसका उत्तर इस त्रिभुज के पैरों की लंबाई के सबसे बड़े सामान्य भाजक के बराबर एक संख्या होगी।


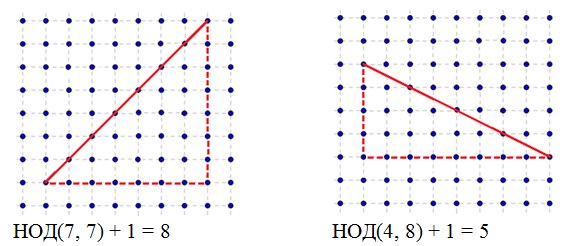
पूर्णांक के पूर्णांक निर्देशांक वाले बहुभुज के लिए, पीक सूत्र मान्य है: S = n + m / 2 - 1, जहां S बहुभुज का क्षेत्रफल है, n बहुभुज के अंदर कड़े पूर्णांक बिंदुओं की संख्या है, m बहुभुज बिंदुओं की संख्या बहुभुज की सीमा पर स्थित है। चूंकि हम जानते हैं कि बहुभुज के क्षेत्र की गणना कैसे की जाती है, एस ज्ञात है। हम बहुभुज की सीमा पर स्थित पूर्णांक बिंदुओं की संख्या की गणना भी कर सकते हैं, इसलिए पीक सूत्र में केवल एक अज्ञात अज्ञात है जिसे हम पा सकते हैं।
एक उदाहरण पर विचार करें:

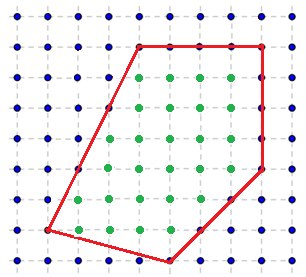
एस = 16 + 4 + 4.5 + 6 + 1 + 2 = 33.5
एम = 15
n = 33.5 - 7.5 +1 = 27 - अंक बहुभुज के अंदर सख्ती से झूठ बोलते हैं
तो यह समस्या हल हो गई!

वह सब है! मुझे उम्मीद है कि आपको लेख पसंद आया होगा, और मैं इसका दूसरा भाग लिखूंगा।