कम्प्यूटेशनल ज्यामिति, या मैं ओलंपियाड प्रोग्रामिंग में कैसे शामिल हो गया। भाग २

प्रविष्टि

कम्प्यूटेशनल ज्यामिति पर मेरे लेख का यह दूसरा भाग है। मुझे लगता है कि यह लेख पिछले एक की तुलना में अधिक दिलचस्प होगा, क्योंकि कार्य थोड़े अधिक जटिल होंगे।

आइए रेखा, किरण और रेखा खंड के सापेक्ष बिंदु की सापेक्ष स्थिति से शुरू करें।

टास्क नंबर 1

बिंदु और रेखा की सापेक्ष स्थिति का निर्धारण करें: रेखा के ऊपर, रेखा के नीचे, रेखा के नीचे स्थित है।

निर्णय
यह स्पष्ट है कि यदि रेखा इसके समीकरण अक्ष + + c = 0 द्वारा दी गई है, तो हल करने के लिए कुछ भी नहीं है। यह लाइन के समीकरण में बिंदु के निर्देशांक को प्रतिस्थापित करने के लिए पर्याप्त है और यह जांचता है कि यह किसके बराबर है। यदि यह शून्य से अधिक है, तो बिंदु ऊपरी आधे तल में है, यदि यह शून्य के बराबर है, तो बिंदु एक सीधी रेखा पर है और यदि यह शून्य से कम है, तो बिंदु निचले आधे तल में है। एक दिलचस्प मामला है जब लाइन दी जाती है, दो बिंदुओं के निर्देशांक को देखते हुए, हम उन्हें पी ₁ (एक्स ₁ , वाई ₁ ), पी ₂ (एक्स ₂ , वाई ₂ ) कहते हैं। इस मामले में, आप सुरक्षित रूप से गुणांक a, b और c ढूँढ सकते हैं और पिछले तर्क को लागू कर सकते हैं। लेकिन हमें पहले सोचना चाहिए, क्या हमें इसकी आवश्यकता है? बिल्कुल नहीं! जैसा कि मैंने कहा कि तिरछा काम करता है - यह सिर्फ कम्प्यूटेशनल ज्यामिति का मोती है। चलो इसे लागू करते हैं। यह ज्ञात है कि दो वैक्टरों का तिरछा उत्पाद सकारात्मक है यदि पहली वेक्टर से दूसरी में घुमाव वामावर्त जाता है, तो यह शून्य के बराबर है यदि घुमाव दक्षिणावर्त है और नकारात्मक है। इसलिए, यह वैक्टर पी ₁ पी ₂ और पी ₁ एम के तिरछा उत्पाद की गणना करने और इसके संकेत द्वारा निष्कर्ष निकालने के लिए पर्याप्त है।

टास्क नंबर 2

निर्धारित करें कि बिंदु बीम से संबंधित है या नहीं।

निर्णय
आइए हम याद रखें कि एक किरण क्या है: एक किरण एक सीधी रेखा है, जो एक तरफ एक बिंदु द्वारा सीमित है, और दूसरी तरफ, अनंत है। यही है, किरण को कुछ शुरुआती बिंदु और उस पर पड़े किसी भी बिंदु से परिभाषित किया जाता है। बिंदु P ₁ (x ₁ , y ₁ ) किरण की शुरुआत होने दें, और P ₂ (x ₂ , y ₂ ) किरण से संबंधित कोई भी बिंदु हो। यह स्पष्ट है कि यदि बिंदु किरण से संबंधित है, तो यह इन बिंदुओं से गुजरने वाली रेखा से संबंधित है, लेकिन इसके विपरीत नहीं। इसलिए, एक सीधी रेखा से संबंधित एक किरण के लिए एक आवश्यक लेकिन पर्याप्त स्थिति नहीं है। इसलिए, हम तिरछे उत्पाद की जाँच से दूर नहीं हो सकते। एक पर्याप्त स्थिति के लिए, एक ही वैक्टर के स्केलर उत्पाद की गणना करना भी आवश्यक है। यदि यह शून्य से कम है, तो बिंदु किरण से संबंधित नहीं है, यदि यह नकारात्मक नहीं है, तो बिंदु किरण पर स्थित है। ऐसा क्यों? आइए तस्वीर को देखें।



तो, बिंदु M (x, y) के लिए किरण पर प्रारंभिक बिंदु P ₁ (x ₁ , y ₁ ) के साथ झूठ बोलने के लिए, जहां P ₂ (x ₂ , y ₂ ) किरण पर स्थित है, दो स्थितियाँ आवश्यक और पर्याप्त हैं:
1. [पी ₁ पी ₂ , पी ₁ एम] = 0 - तिरछा उत्पाद (बिंदु एक पंक्ति पर स्थित है)
2. (पी ₁ पी ₂ , पी ₁ एम) scal 0 - स्केलर उत्पाद (बिंदु किरण पर स्थित है)

टास्क नंबर 3

निर्धारित करें कि बिंदु खंड से संबंधित है या नहीं।

निर्णय
बता दें कि P ₁ (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ) किसी दिए गए सेगमेंट के सिरे हैं। फिर से, एक खंड के लिए एक बिंदु के लिए एक आवश्यक शर्त यह है कि यह पी ₁ , पी ₂ से गुजरने वाली रेखा के अंतर्गत आता है। अगला, हमें यह निर्धारित करने की आवश्यकता है कि बिंदु P ₁ और P _{2 के} बीच स्थित है, इसके लिए हमें केवल इस बार वैक्टर के स्केलर उत्पाद की आवश्यकता है: (MP ₁ , MP ₂ )। यदि यह शून्य से कम या इसके बराबर है, तो बिंदु खंड पर है, अन्यथा खंड के बाहर है। ऐसा क्यों? आइए तस्वीर को देखें।



तो, बिंदु M (x, y) के लिए खंड P1 (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ) के साथ झूठ बोलने के लिए, यह आवश्यक है और पर्याप्त है कि निम्नलिखित स्थितियां संतुष्ट हैं:
1. [पी ₁ पी ₂ , पी ₁ एम] = 0 - तिरछा उत्पाद (बिंदु एक पंक्ति पर स्थित है)
2. (एमपी ₁ , एमपी ₂ ) - 0 - स्केलर उत्पाद (बिंदु पी ₁ और पी _{2 के} बीच स्थित है)

टास्क नंबर 4

दो बिंदुओं की सापेक्ष स्थिति अपेक्षाकृत सीधी है।

निर्णय
इस समस्या में, सीधी रेखा के सापेक्ष एक या अलग-अलग पक्षों पर दो बिंदुओं को निर्धारित करना आवश्यक है।



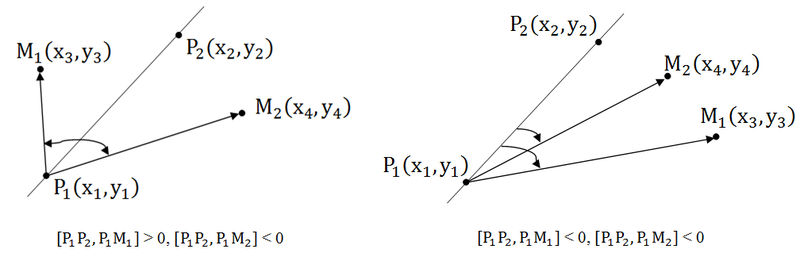
यदि अंक अपेक्षाकृत सीधी रेखा के विपरीत दिशा में हैं, तो तिरछा उत्पादों के अलग-अलग संकेत होते हैं, जिसका अर्थ है कि उनका उत्पाद नकारात्मक है। यदि अंक सीधी रेखा के सापेक्ष एक तरफ झूठ बोलते हैं, तो तिरछा उत्पादों के संकेत मेल खाते हैं, जिसका अर्थ है कि उनका उत्पाद सकारात्मक है।
तो:
1. [पी ₁ पी ₂ , पी ₁ एम ₁ ] * [पी ₁ पी ₂ , पी ₁ एम ₂ ] <0 - बिंदु विपरीत पक्षों पर झूठ बोलते हैं।
2. [पी ₁ पी ₂ , पी ₁ एम ₁ ] * [पी ₁ पी ₂ , पी ₁ एम ₂ ]> 0 - एक तरफ झूठ बोलते हैं।
3. [P ₁ P ₂ , P ₁ M ₁ ] * [P ₁ P ₂ , P ₁ M ₂ ] = 0 - एक अंक (या दो) एक रेखा पर स्थित है।

वैसे, एक सीधी रेखा और एक खंड के बीच एक चौराहे बिंदु की उपस्थिति का निर्धारण करने की समस्या बिल्कुल उसी तरह से हल की गई है। अधिक सटीक रूप से, यह एक ही समस्या है: एक खंड और एक रेखा प्रतिच्छेद जब खंड के छोर रेखा के विपरीत दिशा में होते हैं या जब खंड के छोर रेखा पर स्थित होते हैं, अर्थात, [P ₁ P ₂ , P ₁ M ₁ ] * [P _{1 की आवश्यकता होती है} पी ₂ , पी ₁ एम ₂ ] M 0।

टास्क नंबर 5

निर्धारित करें कि क्या दो लाइनें प्रतिच्छेद करती हैं।

निर्णय
हम मानते हैं कि रेखाएँ मेल नहीं खाती हैं। यह स्पष्ट है कि लाइनें केवल समानांतर नहीं होती हैं यदि वे समानांतर हैं। इसलिए, समानता की स्थिति को देखते हुए, हम यह निर्धारित कर सकते हैं कि क्या रेखाएं प्रतिच्छेद करती हैं।
मान लीजिए कि रेखाएँ उनके समीकरणों द्वारा ₁ x + b ₁ y + c ₁ = 0 और ₂ x + b ₂ y + c ₂ = 0. हैं, तो समानांतर रेखाओं के लिए शर्त यह है कि ₁ b ₂ - a ₂ b ₁ = 0।
यदि अंक P ₁ (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ), M ₁ (x ₃ , y ₃ ), M ₂ (x ₄ , y ₄ ) द्वारा दिए गए हैं, तो उनकी समानता के लिए स्थिति है वैक्टर पी ₁ पी ₂ और एम ₁ एम ₂ के तिरछा उत्पाद की जांच में: यदि यह शून्य है, तो लाइनें समानांतर हैं।



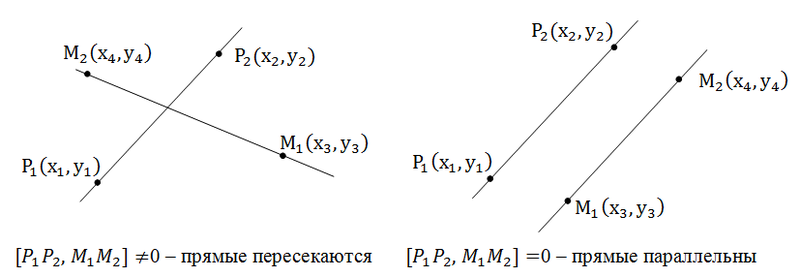
सामान्य तौर पर, जब रेखाएं उनके समीकरणों द्वारा दी जाती हैं, तो हम वैक्टर (-b ₁ , a ₁ ), -b ₂ , a ₂ ) के तिरछे उत्पाद की भी जांच करते हैं, जिन्हें निर्देशन वेक्टर कहा जाता है।

टास्क नंबर 6

निर्धारित करें कि क्या दो खंड प्रतिच्छेद करते हैं।

निर्णय
मुझे वास्तव में यह कार्य पसंद है। खंड तब खंडित होते हैं, जब प्रत्येक खंड के छोर दूसरे खंड के अलग-अलग हिस्सों में होते हैं। आइए तस्वीर को देखें:



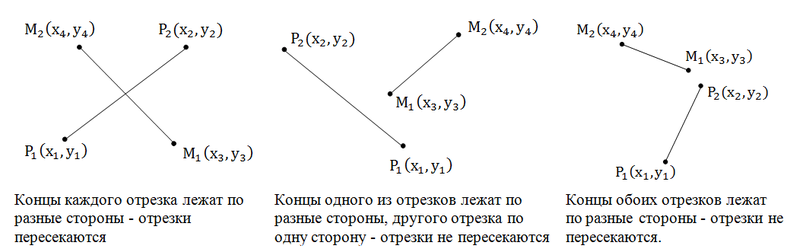
इसलिए, हमें यह जांचने की जरूरत है कि प्रत्येक खंड के छोर दूसरे खंड के सापेक्ष छोरों के विपरीत हैं। हम वैक्टर के तिरछे उत्पाद का उपयोग करते हैं। पहला आंकड़ा देखें: [P ₁ P ₂ , P ₁ M ₂ ]> 0, [P ₁ P ₂ , P ₁ M ₁ ] <0 => [P ₁ P ₂ , P ₁ M ₂ ] * [P ₁ P ₂ , पी ₁ एम ₁ ] <0 इसी तरह
[एम _१ एम _२ , एम _१ पी _१ ] * [एम _१ एम _२ , एम _१ पी _२ ] <० आप शायद सोचते हैं कि यह कम या बराबर क्यों नहीं है। और क्योंकि निम्नलिखित मामला संभव है, जिसमें वेक्टर उत्पाद शून्य के बराबर है, लेकिन सेगमेंट प्रतिच्छेद नहीं करते हैं:



इसलिए, हमें एक और जांच करने की आवश्यकता है, जिसका नाम है: चाहे प्रत्येक खंड का कम से कम एक छोर दूसरे का हो (बिंदु खंड का है)। हमने इस समस्या का हल पहले ही निकाल लिया है।

इसलिए, सेगमेंट में सामान्य अंक होने के लिए यह आवश्यक और पर्याप्त है:
1. खंडों के सिरे दूसरे खंड के सापेक्ष अलग-अलग तरफ होते हैं।
2. एक खंड के कम से कम एक खंड दूसरे खंड का है।

टास्क नंबर 7

एक बिंदु से एक रेखा की दूरी।

निर्णय
लाइन को दो बिंदुओं P ₁ (x ₁ , y ₁ ) और P ₂ (x ₂ , y ₂ ) द्वारा दिया जाए।



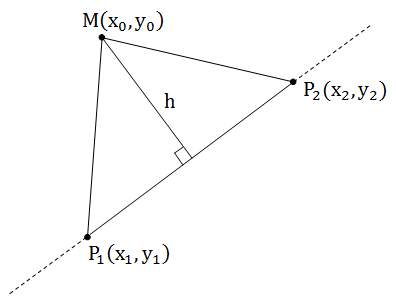
पिछले लेख में, हमने इस तथ्य के बारे में बात की थी कि ज्यामितीय रूप से तिरछा उत्पाद एक समांतर चतुर्भुज का एक उन्मुख क्षेत्र है, इसलिए S _{P 1 P 2 M} = 0.5 * [P ₁ P ₂ , P ₁ M] है। दूसरी ओर, प्रत्येक छात्र एक त्रिभुज का क्षेत्रफल ज्ञात करने का सूत्र जानता है: ऊँचाई का आधा आधार।
एस _{पी 1 पी 2 एम} = 0.5 * एच * पी ₁ पी ₂ ।
इन क्षेत्रों की बराबरी, हम पाते हैं

मोडुलो को लिया गया क्योंकि पहला क्षेत्र उन्मुख है।

यदि रेखा समीकरण कुल्हाड़ी + द्वारा + c = 0 द्वारा दी गई है, तो दिए गए रेखा के बिंदु M लंबवत से गुजरने वाली रेखा का समीकरण है: a (y - y ₀ ) - b (x - x ₀ ) = 0. अब हम आसानी से सिस्टम से हल कर सकते हैं समीकरण, उनका प्रतिच्छेदन बिंदु पाते हैं और आरंभिक बिंदु से मिली दूरी की दूरी की गणना करते हैं: यह बिल्कुल ρ = (अक्ष ₀ + बाय ₀ + c) / √ (एक ² + b ² ) होगा।

टास्क नंबर 8

बीम से बिंदु की दूरी।

निर्णय
यह कार्य पिछले एक से अलग है कि यह इस मामले में हो सकता है, ताकि बिंदु से लंबवत बीम पर न गिर जाए, लेकिन इसकी निरंतरता पर पड़ता है।



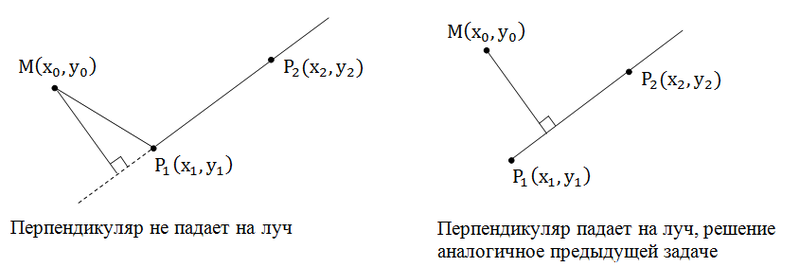
मामले में जब लंबवत बीम पर नहीं गिरता है, तो बीम से शुरुआत तक की दूरी को खोजने के लिए आवश्यक है - यह समस्या का जवाब होगा।

यह कैसे निर्धारित किया जाए कि लंब बीम पर पड़ता है या नहीं? यदि लंबवत बीम पर नहीं गिरता है, तो कोण MP ₁ P ₂ , अन्यथा तीव्र (सीधा) है। इसलिए, वैक्टर के स्केलर उत्पाद के संकेत से, हम यह निर्धारित कर सकते हैं कि लंबवत किरण से टकराता है या नहीं:
1. (पी ₁ एम, पी ₁ पी ₂ ) <0 लंबवत बीम को हिट नहीं करता है
2. (पी ₁ एम, पी ₁ पी ₂ ) per 0 लंबवत बीम को मारता है

टास्क नंबर 9

एक बिंदु से एक रेखा की दूरी।

निर्णय
हम पिछली समस्या के समान हैं। यदि सीधा खंड पर नहीं गिरता है, तो इसका उत्तर इस बिंदु से खंड के अंत तक न्यूनतम दूरी होगी।



यह निर्धारित करने के लिए कि क्या एक लंबवत एक खंड पर पड़ता है, पिछले कार्य के साथ सादृश्य द्वारा वैक्टर के स्केलर उत्पाद का उपयोग करना आवश्यक है। यदि लंब खंड पर नहीं गिरता है, तो या तो कोण MP ₁ P ₂ या कोण MP ₂ P ₁ को भ्रमित किया जाएगा। इसलिए, स्केलर उत्पादों के संकेत से, हम यह निर्धारित कर सकते हैं कि लंबवत खंड पर पड़ता है या नहीं:
यदि (P ₁ M, P ₁ P ₂ ) <0 या (P ₂ M, P ₂ P ₁ ) <0 तब खंड पर लंबित नहीं होता है।

टास्क नंबर 10

लाइन और सर्कल पर बिंदुओं की संख्या निर्धारित करें।

निर्णय
एक लाइन और एक सर्कल में शून्य, एक या दो चौराहे हो सकते हैं। आइए तस्वीरों को देखें:



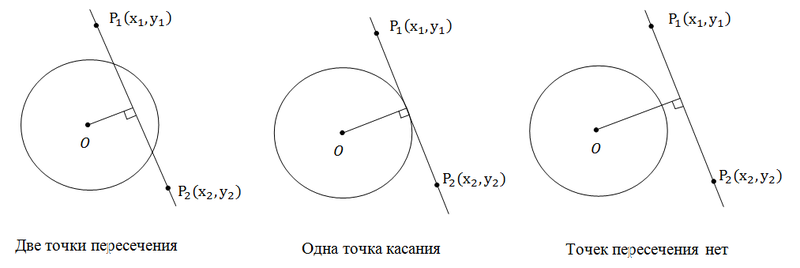
यहां, ड्राइंग से, सब कुछ स्पष्ट है। हमारे पास दो चौराहे बिंदु हैं यदि सर्कल के केंद्र से लाइन की दूरी सर्कल के त्रिज्या से कम है। एक स्पर्श बिंदु यदि केंद्र से लाइन की दूरी त्रिज्या के बराबर है। और अंत में, एक भी चौराहा बिंदु नहीं है यदि सर्कल के केंद्र से लाइन की दूरी सर्कल के त्रिज्या से अधिक है। चूँकि एक बिंदु से एक रेखा की दूरी ज्ञात करने की समस्या हमारे द्वारा पहले ही हल की जा चुकी है, इसलिए यह समस्या भी हल हो गई है।

टास्क नंबर 11

दो मंडलियों की सापेक्ष स्थिति।

निर्णय
मंडलियों की व्यवस्था के संभावित मामले: प्रतिच्छेदन, स्पर्श, प्रतिच्छेद न करें।



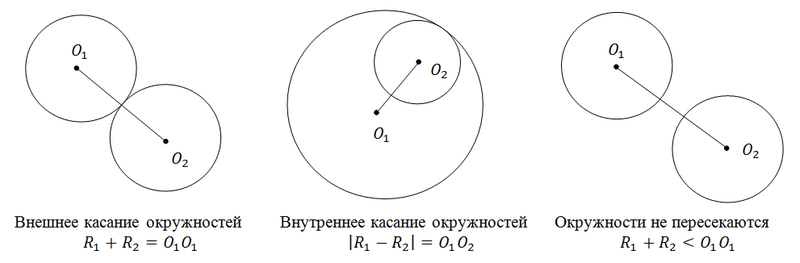
उस स्थिति पर विचार करें जब मंडलियां प्रतिच्छेद करती हैं, और उनके प्रतिच्छेदन का क्षेत्रफल ज्ञात करती हैं। मुझे यह कार्य बहुत पसंद है, क्योंकि मैंने इसे सुलझाने में काफी समय बिताया था (यह बहुत पहले था - पहले साल में)।



अब याद करें कि एक सेक्टर और एक सेगमेंट क्या हैं।


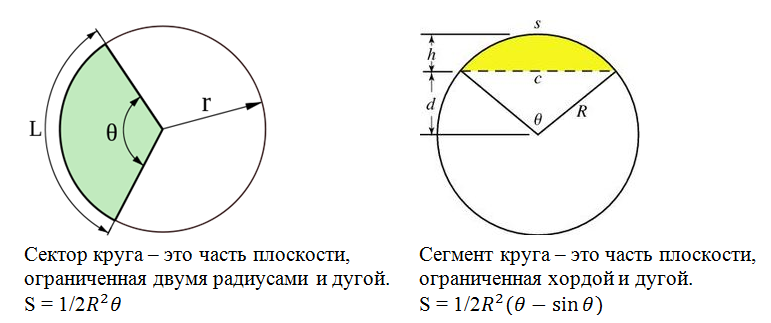
हलकों के चौराहे में दो खंड O ₁ AB और O ₂ AB होते हैं।



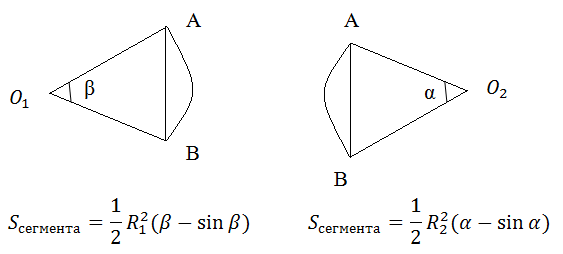
इन क्षेत्रों और सभी के क्षेत्र को जोड़ना आवश्यक प्रतीत होगा। हालांकि, सब कुछ इतना सरल नहीं है। यह निर्धारित करना भी आवश्यक है कि क्या ये सूत्र हमेशा सत्य होते हैं। बाहर मुड़ता है नहीं!

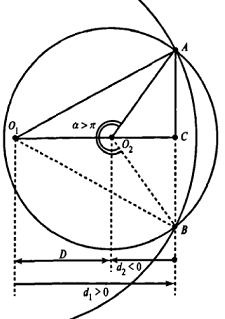
इस मामले पर विचार करें जब दूसरे सर्कल O ₂ का केंद्र बिंदु C. के साथ मेल खाता है। इस मामले में, d ₂ = 0 और α = = मान α के लिए। इस मामले में, हमारे पास एक अर्धवृत्त है जिसका क्षेत्रफल 1/2 haveR ₂ ^{2 है} ।

अब उस मामले पर विचार करें जहां दूसरे सर्कल O ₂ का केंद्र बिंदु O ₁ और C. के बीच है। इस मामले में, हम d ₂ का ऋणात्मक मान प्राप्त करते हैं। D _{2 के} ऋणात्मक मान का उपयोग करने से α का ऋणात्मक मान होता है। इस मामले में, सही उत्तर के लिए α 2 the जोड़ना आवश्यक है।

निष्कर्ष

खैर, यह सब है। हमने सभी पर विचार नहीं किया, लेकिन वस्तुओं की सापेक्ष स्थिति के बारे में कम्प्यूटेशनल ज्यामिति की सबसे अधिक बार सामना करना पड़ा समस्याओं।

मुझे आशा है कि आपको अच्छा लगा होगा।